Multiplicação De Monômio Por Polinômio

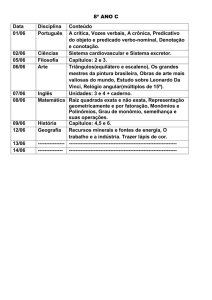
Operações com
1
2
Monômios e Polinômios
0011 0010 1010 1101 0001 0100 1011
4
Adição De Monômios
0011 0010 1010 1101 0001 0100 1011
Efetuar a soma/subtração dos coeficientes
numéricos dos monômios semelhantes.
Ex.:
5x2 – 3ay3 + 7x2 + ay3
5x2 + 7x2
Monômios semelhantes
12x2 – 2ay3
– 3ay3 + ay3
1
2
4
Monômios semelhantes
CUIDADO!!
0011 0010 1010 1101 0001 0100 1011
Na soma de monômios devemos somar
APENAS os coeficientes numéricos. Sendo
assim a parte literal se mantém, ou seja, não
devemos efetuar nenhuma operação com os
expoentes.
Ex.: 4x2 + x2 ≠ 5x4
1
2
4
Multiplicação De Monômios
0011 0010 1010 1101 0001 0100 1011
O produto de monômios é obtido da seguinte
forma:
• primeiro, multiplicam-se os coeficientes
1
numéricos;
• em seguida, multiplicam-se as partes
literais.
2
4
Ex.: (4ax2) . (–13a3x5) =
(4) . (–13) . (a1 . a3) . (x2 . x5) =
– 52a4x7
Lembrando...
0011 0010 1010 1101 0001 0100 1011
Um produto de potências de mesma base pode
ser escrito na forma de uma única potência:
conservamos a base e adicionamos os
expoentes.
am.an = am+n
Ex.: x4.x9 = x4+9 = x13
1
2
4
Divisão De Monômios
0011 0010 1010 1101 0001 0100 1011
A divisão de monômios é obtida da seguinte
forma:
• primeiro, dividem-se os coeficientes
numéricos;
1
2
• em seguida, dividem-se as partes literais.
4
Lembrando...
Um quociente de potências de mesma base
pode ser escrito na forma de uma única
potência: conservamos a base e subtraímos
os expoentes.
0011 0010 1010 1101 0001 0100 1011
am:an = am–n
Ex.: x12 : x8 = x12–8 = x4
1
2
4
Adição De Polinômios
0011 0010 1010 1101 0001 0100 1011
Efetuar a soma algébrica de monômios
semelhantes.
Ex.:
1
2
(4x2 – 7x + 2) + (3x2 + 2x + 3) – (2x2 – x + 6) =
 eliminando os parênteses
4
= 4x2 – 7x + 2 + 3x2 + 2x + 3 – 2x2 + x – 6 =
 agrupando os termos semelhantes
= 4x2 + 3x2 – 2x2 – 7x + 2x + x + 2 + 3 – 6 =
=
5x2
– 4x – 1
* Não esqueça da regra
 forma reduzida de sinal!
Multiplicação De Monômio
Por Polinômio
0011 0010 1010 1101 0001 0100 1011
A multiplicação de um monômio por um polinômio
é feita multiplicando-se o monômio por cada
termo do polinômio.
Ex.:
4x2y3 . (2x3 – 5xy4) =
1
=
8x5y3
–
20x3y7
2
4
= 4x2y3 . 2x3 + 4x2y3 . (– 5xy4 )
* Não esqueça da regra
de sinal!
Multiplicação De Polinômio
Por Polinômio
0011 0010 1010 1101 0001 0100 1011
A multiplicação de um polinômio por outro
polinômio é feita multiplicando-se cada termo
de um deles pelos termos do outro e, sempre
que possível, reduzindo os termos semelhantes.
Ex.:
(a + b) . (c + d) =
ac + ad + bc + bd
1
2
4
Divisão De Polinômio Por Monômio
Efetuamos a divisão de um polinômio por um
monômio fazendo a divisão de cada termo do
polinômio pelo monômio.
0011 0010 1010 1101 0001 0100 1011
Ex.:
(18x3
–
12x2
+ 3x) : (3x) =
1
2
4
= (18x3 : 3x) – (12x2 : 3x) + (3x : 3x)
= 6x2 – 4x + 1
Valor Numérico de uma
Expressão Algébrica
Após obtida a expressão algébrica, basta substituir
cada incógnita pelo valor estabelecido pelo
exercício.
Ex.: Determine o valor numérico da expressão
abaixo para x = 2 e y = 3
3x2 – 2x + 7y + 3x – 17y
0011 0010 1010 1101 0001 0100 1011
1º reduzimos os termos semelhantes
3x2 + x – 10y
3.4 + 2 – 30
12 + 2 – 30 = - 16
2
4
2º substituímos os valores de x = 2 e y = 3
3.22 + 2 – 10.3
1
A mente que se abre a uma nova
idéia jamais voltará ao seu
tamanho original.
0011 0010 1010 1101 0001 0100 1011
1
Albert Einstein
2
4