aula-21 - Unicamp

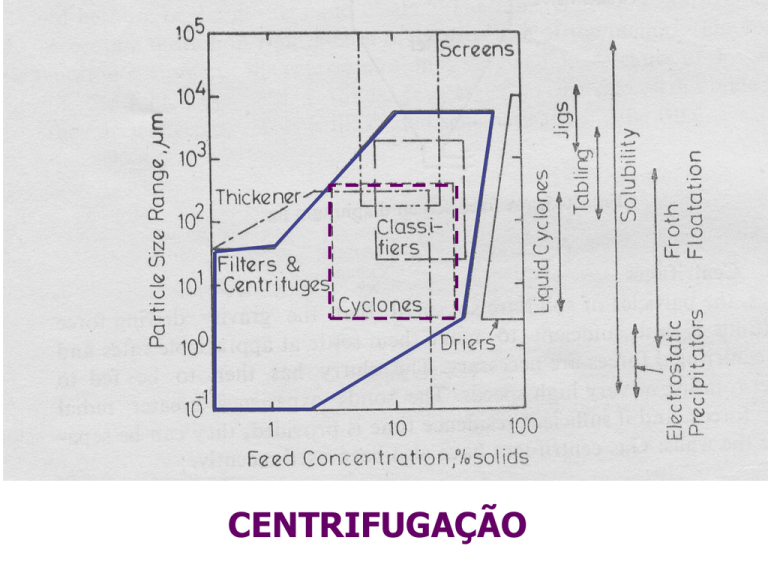
CENTRIFUGAÇÃO
CENTRIFUGAÇÃO
Livro de consulta: Christie John Geankoplis.
Transport Process and Separation Processes.
Prentice-Hall, 2003.
Centrifugação
 Na sedimentação as partículas são separadas de
um fluído por ação da força gravitacional.
 A separação gravitacional pode ser muito lenta
devido a vários fatores:
(a) tamanho pequeno das partículas,
(b) densidades próximas da partícula e do fluido
(c) forças associativas que mantém componentes
ligados (como nas emulsões).
 O uso da força centrífuga aumenta muitas vezes
a força que atua sobre o centro de gravidade das
partículas, facilitando a separação e diminuindo
o tempo de residência no equipamento.
A centrifuga é um recipiente cilíndrico que gira a alta
velocidade criando um campo de força centrífuga
que causa a sedimentação das partículas.
Os fluidos e sólidos podem exercer uma força muito alta
contra à parede do recipiente, esse fato limita o diâmetro
das centrífugas.
Equações de força centrífuga.
A aceleração pela força centrífuga é dada por
ae  r
2
ae é a aceleração devido à força centrífuga (m/s2)
r é a distância radial do centro da rotação (m)
ω é a velocidade angular (radianos / s).
A força centrífuga Fc
Fc  m ae
Fc  m r 
2
ω = velocidade angular
ω = v/r
g
v é a velocidade tangencial (m/s)
As velocidades rotacionais ( N ) costumam ser dadas
em RPM ou seja por rotações/min,
As unidades de ω no SI são radianos por segundo
2 N

60
revoluçoes 2π radianos
1 minuto
ωN


minuto
1 revolução 60 segundos
Substituindo
Fc  m r 
2
 2N 
2
Fc  m r 

0
,
01097
m
r
N

 60 
2
Fg  mg
A força gravitacional
em uma partícula é
Fc  mr
A força centrifuga é
2
Se comparamos ambas equações:
Fc mr
r
r  2 N 


 

Fg
mg
g
g  60 
2
2
2
Assim, a força desenvolvida em uma centrífuga é
rω2/g
vezes maior que a força gravitacional.
Fc
2
2

r  N
Fg 60 g
Fc
2
 0.001118  r  N
Fg
Ex. 1: Aumento da força pela centrifugação
Uma centrífuga tem raio de cilindro de 0.1016 m
e uma velocidade de giro de 1000 RPM
Quantas vezes maior é a força centrifuga
em relação a gravitacional?
Qual seria o efeito na força centrífuga ao
dobrar o raio do equipamento?
Qual seria o efeito de duplicar a velocidade
de rotação?
Fórmula:
Fc
2
 0,001118 r N
Fg
Ex. 1: Resolução
Fc
?
Fg
R = 0.1016 m
N = 1000 RPM
Fórmulas:
R = 2 x 0.1016 m
N = 1000 RPM
Fg  mg
R = 0.1016 m
N = 2000 RPM
 2 N ( rpm) 

  r( m ) 
 60 
Fc  mr
2
2
Fc r 2

Fg
g
Fc
2
 0,001118 r N
Fg
R = 0.1016 m
N = 1000 RPM
Fc
 1,118 103 (0,1016)(1000) 2
Fg
Fc
113
Fg
R = 2 x 0.1016 m
N = 1000 RPM
Fc
 1,118 103 (0,2032)(1000) 2
Fg
Ex. 1: Respostas
R = 0.1016 m
N = 2000 RPM
Fc
 0,001118 r N 2
Fg
Fc
 227
Fg
Fc
3
2
 1,118 10 (0,1016)( 2000)
Fg
Fc
 454
Fg
Taxas de Separação em Centrífugas
Assume-se que :
Todo o líquido se move
para cima à velocidade
uniforme, transportando
partículas sólidas com ele.
As partículas movem-se
radialmente na vt de
sedimentação.
Se o tempo de residência
for suficiente para que a
partícula chegue até
parede do tambor ela é
separada
vs =velocidade de sedimentação
vt =velocidade de transporte
Na região A: vt > vs ocorre transporte sem separação
Na região B: vs > vt separação problemática
Na região C: vs >> vt boa separação
A velocidade terminal de sedimentação, em um raio r,
se o regime for laminar, de acordo com a lei de Stokes
é:
2
2
 rD p  p   
vt 
18
2
2

rD
dr
p  p   

dt
18
Onde
vt = velocidade de sedimentação na direção radial
Dp = diâmetro da partícula
µ = viscosidade do líquido
rp = densidade de partícula r = densidade do líquido
Como vt = dr/dt
É possível converter a equação da velocidade terminal
em uma equação diferencial e depois integrá-la.
Equação do tempo de residência
dr  rD  p   

dt
18
2

t t r
t 0
2
p
18
dt  2
  p   Dp2

r2
r1
dr
r
Integrando entre os limites
para t = 0 r = r1
para t = tr r = r2
18
r2
tr  2
ln
2
  p    Dp
r1
O tempo de residência é igual
ao volume de líquido do
tambor da centrífuga
3
V
m
tr 

3
q
m 
 s 
 
dividido pela vazão
volumétrica da alimentação.
Volume do líquido no
tambor:
V   (r  r ) b
2
2
2
1
Tempo de residência:
18
r2
tr  2
ln
2
  p    Dp
r1
Pode se obter a equação da vazão volumétrica, q :
V
q
tr
Equação da vazão volumétrica
V   (r  r ) b
2
2
2
1
18
r2
tr  2
ln
2
  p    Dp
r1
Substituindo
 br
V
q
tr
Reagrupando termos
q

2



D
p
p
18

r 
q
18 ln r2 / r1 
 2  p   D p2
2
2

2
1
 2  br22  r12 
ln r2 / r1 
As partículas com diâmetro menor que Dp não alcançam
a parede do tambor e saem com o efluente. As partículas
maiores atingem a parede e são separadas.
As partículas menores do Diâmetro
Crítico Dpc não serão retidas
Dpc define-se como o diâmetro de uma
partícula que consegue atingir a
periferia do tambor partindo de uma
distância entre r1 e r2.
A integração é feita considerando que
para t = 0
r = (r1 + r2)/2
em t = tT.
r = r2
  p   D
qc 
18
2
2
pc
br

r 

ln 2r2 / r1  r2 
2
2
2
1
qc  vt  
Na vazão qc as partículas com um diâmetro maior do que Dpc
serão separadas e as menores permanecerão no líquido
Ex.2: Sedimentação em centrífuga
Uma suspensão será clarificada por centrifugação.
Ela contém partículas com densidade ρp= 1461 kg/m3.
A densidade da suspensão é ρ = 801 kg/m3 e sua
viscosidade é 100 cP.
As dimensões da centrífuga são:
r2 = 0.02225 m
r1 = 0.00716 m
altura b = 0.1970 m.
Calcule o diâmetro crítico das partículas
se N = 23000 revoluções/minuto e qc = 0.002832 m3/h.
Ex.2: Resolução
Questão:
Dpc =?
Fórmula:
2
 2  p   Dpc
V 
qc 
18 ln 2r2 / r1  r2 
Dados:
ρp= 1461 kg/m3
ρ = 801 kg/m3
μ = 100 cP
r2 = 0.02225 m,
r1 = 0.00716 m
b = 0.1970 m
N = 23000 rpm
qc = 0.002832 m3/h
D
2
pc
qc 18 ln 2r2 / r1  r2 

 2  p   V 
2N
2 ( 23000)


 2410rad / s
60
260
(23000)



 2410rad / s

60
V   b r  r   0,1970 0,02225

2
2
2
1

V   0,1970 0,02225  0,00716  2,747 x10 4 m3
3
0,002832
m
qc 
 7,87 x107
3600
s
2
2
Dpc  0,746 x106 m  0,746 m
2
Separação de líquidos em uma centrífuga.



A separação de suspensões líquido-líquido compostas
de líquidos imiscíveis que estão finamente dispersos
como uma emulsão são um problema comum na
indústria alimentícia.
Um exemplo é a emulsão de leite que é separada em
dois produtos: leite desnatado e creme ou nata,
usando centrífugas.
Nessas separações, a posição da barreira de
transbordamento na saída da centrífuga é muito
importante na realização da separação desejada. Fora
isso os discos de saída de raio diferente permitem o
ajuste do funcionamento da centrífuga,
Separação de duas fases líquidas:
r4 – r2
 líquido pesado com H
 líquido leve com L
Onde :
r1 = raio até a superfície da
camada do líquido leve.
r2 – r1
r2 = raio até a interface
líquido-líquido.
r4 = raio até a superfície do
fluxo de escoamento
do líquido pesado.
Para localizar a interface entre os líquidos, deve ser
feito um balanço das pressões nas duas camadas.
A força no fluido na distância r é:
Fc  mr
Como
dFc  dmr 2
2
dm[(2 rb) dr] 
dFc  2rb dr  r 
2
Então
A  2rb
dFc 2 rb
2

  rdr
A 2 rb
dP   rdr
2
dP   2 rdr

r r 
2
 

P P 
r r 
2
P2  P1 
Integrando, obtemos:

p2
p1
dP  
2

r2
r1
 L
2
2
2
2
1
2
2
2
H
rdr
4
2
2
4
Na interface líquida em r2, a pressão exercida pela fase leve
de espessura (r2 - r1) é igual à pressão da fase pesada de
espessura (r2 - r4):
H
P2  P1  P4  P2
2
2
(r  r ) 
2
2
2
4
 L
2
2
(r22  r12 )
Resolvendo para r22, na posição da interface, obtemos:
 r  r
r 
H  L
2
2
2
H 4
2
L 1
Ex.3: Altura da interface
Em um processo de refinação de óleo se separa
a fase aquosa da face oleosa em uma centrífuga.
A densidade do óleo é 919,5 kg/m3
A densidade da face aquosa é 980,4 kg/m3
O raio (r1) do escoamento do liquido mais leve é
10,160 mm
O raio (r4) da saída da face pesada é 10,414 mm
Calcule o raio (r2) da interface líquido-líquido
Questão
Ex.3: Solução
Dados
r4 = 10,414 mm
ρL = 919,5 kg/m3
ρH = 980,4 kg/m3
r1 = 10,160 mm
r4 = 10,414 mm
r2 = ?
Formulas
 r  r
r 
H  L
2
2
2
H 4
 r  r
r2 
H  L
H
r1 = 10,160 mm
2
L 1
2
4
r2 13,75 mm
2
L 1
Equipamentos Centrifuga de Tambor
 Utilizada apenas na clarificação
de líquidos.
 O tambor é dotado de 2 a 8
elementos cilíndricos internos,
uma série de câmaras
anelares unidas
consecutivamente.
 O produto a ser clarificado entra no tambor pelo centro,
escoando consecutivamente por cada câmara anelar a
partir da câmara mais interna.
 Em cada câmara o diâmetro é maior e aumenta a força
centrífuga, fazendo o produto escoar por zonas
centrífugas cada vez maiores, até o final do processo.
2. Centrífugas de disco
 Usada em separações
líquido-líquido, algumas
podem separa partículas
finas de sólidos.
 A mistura é alimentada pelo
fundo da centrífuga e escoa
para cima passando através
de buracos espaçados nos
discos.
 Os buracos dividem a seção
vertical em uma seção
interna, onde fica o líquido
leve, e uma seção externa,
onde fica o líquido pesado.
Escolha do separador correto