Problema 2

Problema 2
Sistema haste-balancimválvula
Enunciado
• Nas condições de rotação do
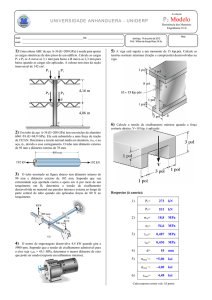
Problema 1, o sistema hastebalancim-válvula se encontra na
posição de admissão indicada na
figura.
As
dimensões
estão
indicadas. O módulo de elasticidade
do aço é de 200 GPa.
Dados
• Haste:
o
o
o
o
Massa de 0,110 kg;
Área da seção de 8,0E-5 m2;
vB=2,6 m/s
(aB)y=1040 m/s2
• Balancim:
o Massa de 0,055 kg;
o Raio de giração de 0,019 m;
• Válvula (2):
o
o
o
o
o
o
Massa de 0,075 kg (cada);
Diâmetro da admissão 0,026 m (cada);
Diâmetro na base de 0,005 m;
Constante de mola de 12,4 kN/m;
Pré-deformação da mola de 0,0042 m;
Pressão de admissão de 9,8.104 Pa;
Análise cinemática
• Hipóteses
– As velocidades vB e vC são
verticais
– Desprezar a inércia do balancim
para efeito dos esforços internos
Análise cinemática
• Velocidades
– Balancim
 

v B    rB / O
 v B  2,6


 153 rad/s
rB / O 0,017
– Válvula
 

v C    rC / O
v C    rC / O  153.0,029  4,4 m/s
Análise cinemática
• Aceleração
– Balancim

  
 
a B      rB / O     rB / O
 a h  1040
2


 61200 rad/s
rB / O 0,017
– Válvula

  
 
a C      rC / O     rC / O
a C  a v  rC / O  61200.0,0029  1770 m/s 2
Equação do movimento: haste
Y  0  Y
A
 YB  m h a h
Equação do movimento: válvula
L
 Y  0  YC  2m v a v  2pA v  2k ( 2  0 )
Equação do movimento: balancim
Y  0  Y  Y
M  0  Y r
O
O
B
B B/ O
 YC  0
 YC rC / O  I G   m b rG2 
Reações
• Substituindo os valores
YA  863 N
YB  749 N
YC  397 N
YO  1146 N
Diagramas de esforços internos
+

+
Análise de
geométricas
tensão
normal:
propriedades
• Momento de inércia
10.123
Iz 
 1,44.10 9 m 4
12
• Módulo de resistência
9
I z 1,44.10
Wz  
 2,40.10 7 m 3
c
0,006
Análise de tensão normal: perfil em O
y
53 MPa
x
6 mm
eixo neutro
6 mm
53 MPa
• Perfil de tensão normal
x 
 Mz
 12,7
y
y  8819 y [MPa]
9
Iz
1,44.10
Análise de tensão de cisalhamento: momentos
estáticos
• Momento estático da figura
hachurada
h



y

 h

b  y 
I z   y CG h A h   y  2
2  2





 1,8.10 7  5,0.10 3 y 2 [m 3 ]
Análise de tensão de cisalhamento: perfil
• Perfil de tensão de cisalhamento
Q I z
749 1,8.10 7  5,0.10 3 y 2 
 xy 


I z t 1,44.10 9
0,010
 9,36  2,60.105 y 2 [MPa]
Análise do estado de tensão na seção crítica
• Ponto na periferia da seção
y
6 mm
53 MPa
eixo neutro
x
6 mm
53 MPa
 x  53 MPa
 y   xy  0
• Círculo de Mohr
 (MPa)
26,5
Estado uniaxial
-53
 (MPa)
-26,5
26,5
26,5
Análise do estado de tensão na seção crítica
• Ponto sobre o eixo neutro
y
9,4 MPa
6 mm
x y  0
eixo neutro
x
 xy  9,4 MPa
6 mm
yx
y
x
xy
• Círculo de Mohr
Estado de cisalhamento puro
 (MPa)
9,4
9,4  (MPa)
9,4
-9,4
0
-9,4
Análise do estado de tensão na seção crítica
• Ponto intermediário
7 MPa
y
26,5 MPa
6 mm
eixo neutro
3 mm
x
6 mm
 x  26,5 MPa
y 0
 xy  7,0 MPa
• Círculo de Mohr
Estado de cisalhamento puro
 (MPa)
27,4
40,7
14,1
-40,7
(-26.5,-7)
-13,3 0 14,1  (MPa)