Slide 1 - Aprender

Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Professores
FADIGA DE MATERIAIS
• Jorge Luiz A. Ferreira
•
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Sumário
•Fadiga Oligocíclica x Fadiga Policíclica
•Comportamento Cíclico do Material
•A Curva - Cíclica
•A Curva -N
•Propriedades Cíclicas dos Materiais
•Método das Deformações Locais
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Fadiga Oligocíclica (-N) x Fadiga Policíclica (S-N):
Fadiga Oligocíclica
Fadiga Policíclica
• Controlada pelas deformações.
• Baixo num. de ciclos (< 1000 ciclos)
• Quando a trinca inicia ?
• Mais difícil de lidar no projeto.
• Controlada pelas tensões.
• Num de ciclos > 1000 ciclos.
• Quando a peça rompe ?
• Mais fácil de lidar no projeto.
Vantagens:
• Mais conservativo.
• Largamente utilizada na indústria.
• Cobre toda a faixa de vida
Vantagens:
• Parâmetros empíricos para muitos
materiais já determinados.
• Fácil aplicação.
Desvantagens:
• Análise fortemente dependente de
dados experimentais.
• Aplicação mais complicada.
• Custo de uso mais elevado
Desvantagens:
•Não pode ser usada para condições de
fadiga oligocíclica.
• resultados não-conservativos para
carregamentos de amplitudes variáveis.
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Hipóteses Básicas
A idéia fundamental da análise de vida por
deformações é que a vida a fadiga pode ser
determinada examinando-se as relações entre
amplitude de deformações (D/2) e número de
reversões de carga (2N) para iniciação de uma
trinca de fadiga.
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Comportamento Monotônico dos Materiais Metálicos
Diagrama Tensão-Deformação Convencional
•
A
tensão
nominal,
ou
tensão
de
engenharia,
é
determinada pela divisão da carga aplicada F pela área
original da seção transversal do corpo de prova, A0:
•
A deformação nominal, ou deformação de engenharia, é
determinada pela divisão da variação δ no comprimento
de referência do corpo de prova, pelo comprimento de
referência original do corpo de prova, L0.
F
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Comportamento Monotônico dos Materiais Metálicos
Diagrama Tensão-Deformação Convencional
•
A tensão nominal, ou tensão de engenharia, é
determinada pela divisão da carga aplicada F pela
área original da seção transversal do corpo de
prova, A0:
•
A
deformação
nominal,
ou
deformação
de
engenharia, é determinada pela divisão da variação
δ no comprimento de referência do corpo de prova,
pelo comprimento de referência original do corpo
de prova, L0.
P
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Comportamento Monotônico dos Materiais Metálicos
Característica e Propriedades do Diagrama Tensão-Deformação
• Região Elástico:
Trecho em que a tensão varia de 0 a Sp. Nesta fase a
inclinação da curva é constante, sendo medida pela relação entre “S” e “e” e
recebe o nome de módulo de elasticidade longitudinal ou módulo de Young (E).
S
su
sf
sy
sp
Su : Limite de Resistência
• Patamar de Escoamento:
Sf : Resistência na Fratura Sp: Limite de Proporcionalidade
A partir do instante em que a tensão
ultrapassa o limite de proporcionalidade, o material apresenta comportamento
e
plástico. Ou seja, ocorrem deformações crescentes na peça sem acréscimos na
tensão. O valor desta tensão constante recebe o nome de limite de elasticidade
,ou de escoamento, (Sy).
• Região Elastoplástica:
Sy: Limite de Elástico
definida a partir do fim da região elástica até
Sy
a ruptura do material. O comportamento mecânico do material durante o
desenvolvimento das tensões nessa região, não permite o retorno do corpo-deprova à sua forma e dimensões originais, quando da ausência de carga aplicada.
0,2%
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Comportamento Monotônico dos Materiais Metálicos
Característica e Propriedades do Diagrama Tensão-Deformação
• Resistência a Tração, Su:
é indicada pelo ponto de máxima tensão
observado na curva de tensão-deformação e, em geral, indica quando o início de
estricção (necking) do corpo de prova se inicia.
• Região de Encruamento:
su
sf
sy
sp
Localiza-se entre o final do processo de
escoamento e o início da estricção. Caracteriza-se pelo processo de
endurecimento por deformação (o que resulta em uma curva que cresce
continuamente, mas torna-se mais achatada até atingir o limite de resistência a
tração).
• Região de Estricção:
S
Su : Limite de Resistência
Sy: Limite de Elástico
Sf : Resistência na Fratura Sp: Limite de Proporcionalidade
e
Inicia-se quando começa a ocorrer uma redução
localizada da secção transversal do corpo de prova (típico em aços dúcteis) e
termina quando a peça fratura. A ruptura sempre se dá na região mais estreita
do material a uma tensão aparentemente inferior ao limite de resistência a
tração do material.
A estricção começa no ponto de instabilidade plástica onde o aumento da resistência devido ao encruamento cai para compensar a
diminuição da área da seção reta transversal do corpo de prova. Isso ocorre na carga máxima ou quando a deformação verdadeira
se iguala ao coeficiente de encruamento. A formação de um empescoçamento introduz um estado de tensões triaxial nessa região.
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Comportamento Monotônico dos Materiais Metálicos
Característica e Propriedades do Diagrama Tensão-Deformação
• Coeficiente de Poisson, n:
Além da deformação longitudinal, ao se aplicar
uma carga P no corpo de prova, se observa a
variação
simultânea
das
dimensões
Área A
transversais do espécime, de sinal oposto,
sendo a deformação específica transversal (ou
lateral) dada por
A
t 
A0
Define-se, assim, o coeficiente de Poisson
como a razão entre a deformação transversal
e a deformação longitudinal.
A-dA
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Comportamento Monotônico dos Materiais Metálicos
Diagrama Tensão-Deformação Real (ou Verdadeira)
Conforme discutido anteriormente, a tensão de engenharia, é estimada pela relação entre a
carga aplicada P e a área inicial da seção transversal do corpo de prova, A0, enquanto que a
deformação relaciona-se ao comprimento inicial da seção reduzida.
Como consequência da adoção dos parâmetros A0 e L0, a curva tensão versus deformação,
bem como, as propriedades mecânicas definidas anteriormente podem não representar de
forma adequada o comportamento verdadeiro do o material – Em especial, na caracterização
de metais dúcteis que são mais suscetíveis a ocorrência de estricção, que é uma condição
que instabiliza completamente a distribuição das deformações pelo estado triplo de tensões
que se estabelece na região.
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Comportamento Monotônico dos Materiais Metálicos
Diagrama Tensão-Deformação Real (ou Verdadeira)
Definição da Deformação Real (ou verdadeira)
A deformação real é baseada na variação do comprimento com relação ao comprimento base
de medida a cada instante, em vez do comprimento inicial de medida. Assim sendo, com a
aplicação de uma carga, Pi, o comprimento inicial passa de L0 para Li. Aumentando a carga em
∆P, aumenta o comprimento em dL. Assim, a deformação verdadeira será definida como a
relação entre a dLi e Li. Para o caso de um aumento da carga de 0 a P e do comprimento
inicial indo desde L0 até L, a deformação verdadeira, , será expressa como:
Como:
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Comportamento Monotônico dos Materiais Metálicos
Diagrama Tensão-Deformação Real (ou Verdadeira)
Definição da Tensão Real
Define-se tensão real como a relação entre a
força F e a área da seção transversal do
corpo-de-prova no mesmo instante que F é Reescrevendo a tensão verdadeira como:
aplicada , Ai, isto é:
Chega-se a seguinte relação:
Como
o
volume
do
aproximadamente
plástica, tem-se que:
material
constante
permanece
na
região
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Comportamento Monotônico dos Materiais Metálicos
Diagrama Tensão-Deformação Real (ou Verdadeira)
Curva Tensão deformação
Real (, )
Curva Tensão deformação de
Engenharia (S, e)
E = Módulo de Elasticidade
Sy= Tensão de Escoamento
Su= Limite de Resistência a Tração (=
Pmax/Ao)
 = Resistência Verdadeira na Fratura
%RA = Redução Percentual da área (=
100 (Ao–Af)/Ao)
f= Deformação (ou ductilidade)
Verdadeira na Fratura = ln (Ao/Af) = ln
[100/(100 -%RA)]
%EL= Alongamento Percentual
= 100 (lf–lo)/lo
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Comportamento Monotônico dos Materiais Metálicos
Diagrama Tensão-Deformação Real (ou Verdadeira)
Curva Tensão deformação
Real (, )
Curva Tensão deformação de
Engenharia (S, e)
Usos e Limitações das Relações entre tensão e
deformação
Fator de Correção
de Bridgman
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Comportamento Monotônico dos Materiais Metálicos
Diagrama Tensão-Deformação Real – Recuperação Elástica

• Após o corpo de prova ser carregado além do limite de
escoamento, o material experimentará uma deformação
permanente que não é recuperada após o descarregamento.
• A curva de descarregamento é linear e paralela ao curva
elástica observada no processo de carregamento.
• Assim, a deformação total, , pode ser dividida em duas
componentes específicas:
• Deformação elástica, e= /E, e
 • Deformação plástica, p.
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Comportamento Monotônico dos Materiais Metálicos
Diagrama Tensão-Deformação Real – Relação Funcional

Se construirmos o diagrama de dispersão entre a tensão
aplicada e a deformação plástica resultante, verificaremos
que em escala log-log, os pontos experimentais tenderão a
ser bem representados por meio de uma linha reta (isso é
especialmente verdadeiro para muitos metais).
Isso significa que a 
função matemática
mais adequada para
representar os dados
experimentais é uma
 função de potência.
p

Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Comportamento Monotônico dos Materiais Metálicos
Diagrama Tensão-Deformação Real – Relação Funcional
Assim, considerando que, na maioria das vezes, a função
de potência representa de forma adequada a relação entre
a deformação plástica e a tensão, a deformação total pode
ser expressa pela seguinte relação:

t  e   p 

 
 
E K
1
n
E – Módulo de Elasticidade

K – Coeficiente de Resistência (representa a tensão necessária para
induzir uma deformação plástica igual a 1)
n – Expoente de endurecimento do material
Esse tipo de relação é conhecida como relação de Ramberg-Osgood
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Comportamento Cíclico dos Materiais Metálicos
Os metais, quando submetidos a
carregamentos
que
induzem
deformações plásticas reversíveis,
exibem
um
comportamento,
designado
de
“comportamento
cíclico”,
que
é
distinto
do
comportamento
monotônico
do
material (relacionado a aplicação
de carregamentos estáticos).
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Comportamento Cíclico dos Materiais Metálicos
Determinação Experimental da
Curva - Cíclica
Comportamentos cíclicos típicos:
a) endurecimento cíclico;
b) amolecimento cíclico;
c) Relaxação cíclica da tensão média;
d) fluência cíclica
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Comportamento Cíclico dos Materiais Metálicos
Determinação Experimental da
Curva - Cíclica
Mecanismos de Endurecimento e Amolecimento cíclico
Existem diversos mecanismos que poder induzir
esses comportamentos, mas o principal está
relacionado a movimentação e interação de
discordâncias
Materiais macios ou recozidos, a densidade de
discordâncias é baixa. Com o carregamento a
densidade tende a aumentar rapidamente
contribuindo para o endurecimento cíclico.
Imagens MET da amostra original da fase Mg2Si
(b) e interação entre discordâncias devido a
aplicação de esforços com amplitude de tensão
igual a 115 MPa [Xiao-song et al (2011)]
O endurecimento cíclico provoca o aumento de resistência à deformação do material ao
decorrer do ensaio. Para manter a amplitude de deformação constante é necessário um
acréscimo gradativo no valor da tensão.
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Comportamento Cíclico dos Materiais Metálicos
Determinação Experimental da
Curva - Cíclica
Mecanismos de Endurecimento e Amolecimento cíclico
Existem diversos mecanismos que poder induzir
esses comportamentos, mas o principal está
relacionado a movimentação e interação de
discordâncias
Já em materiais encruados, o carregamento cíclico
pode causar um rearranjo de discordância em uma
configuração que induz uma menor resistência a
deformação, ou seja um amolecimento.
(estrutura tipica discordancias)
estrutura das discordâncias
depois de 200 ciclos de tensão
HUI-FEN CHAI and CAMPBELL LAIRD, “Mechanisms of
Cyclic Softening and Cyclic Creep in Low Carbon Steel”,
Materials Science and Engineering, 93 (1987) 159-174
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Comportamento Cíclico dos Materiais Metálicos
Determinação Experimental da
Curva - Cíclica
Identificação do processo durante o ensaio
Febara, 2016 (Não publicado)
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Comportamento Cíclico dos Materiais Metálicos
Determinação Experimental da
Curva - Cíclica
Mecanismos Relaxação Cíclica da Tensão Média;
Alguns materiais quando submetidos a cargas com
tensão média diferente de zero, podem apresentar um
comportamento transiente adicional. Exemplo de tal
comportamento é apresentado nas figuras ao lado.
Abordaremos esse comportamento um pouco mais na frente quando
trabalharmos a construção da curva tensão deformação ciclica.
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Comportamento Cíclico dos Materiais Metálicos
Determinação Experimental da Curva - Cíclica
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Comportamento Cíclico dos Materiais Metálicos
Na Ausência de Resultados Experimentais, Como Identificar como
Material Vai se Comportar Ciclicamente ?
Regra prática 1:
• Srt / Sy > 1,4
• Srt / Sy < 1,2
O material endurecerá ciclicamente.
O material amolecerá ciclicamente.
Regra prática 2:
•
•
n> 0.20
n< 0.10
O material endurecerá ciclicamente.
O material amolecerá ciclicamente.
o
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Comportamento Cíclico dos Materiais Metálicos
Efeito Bauschinger
O fenômeno, conhecido como efeito
Bauschinger, consiste na diminuição
da tensão de escoamento quando,
após a deformação em uma dada
direção,
ocorre
direção oposta
deformação
na
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Comportamento Cíclico dos Materiais Metálicos
Efeito Bauschinger
O fenômeno, conhecido como efeito Bauschinger, consiste na diminuição da
tensão de escoamento quando, após a deformação em uma dada direção,
ocorre deformação na direção oposta
Johann Bauschinger
( 1834 - 1893
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Comportamento Cíclico dos Materiais Metálicos
Efeito Bauschinger

Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Comportamento Cíclico dos Materiais Metálicos
Efeito Bauschinger
O efeito Bauschinger está normalmente associada com as
condições em que a resistência à deformação de um metal
diminui quando a direção da deformação é alterada. É um
fenômeno geral encontrado na maioria dos metais policristalinos.
O seu mecanismo básico está relacionado com a estrutura das
discordâncias
no
metal
trabalhado
a
frio.
Como
ocorre
deformação, os deslocamentos irá acumular nas barreiras e
produzir empilhamento e emaranhado das discordâncias.
https://www.youtube.com/watch?v=r-geDwE8Z5Y

Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Comportamento Cíclico dos Materiais Metálicos
Modelo de Endurecimento do Material
Critério de Escoamento de Mises:
Prevê que o escoamento ocorrerá sempre que a energia
de distorção acumulada em elemento de volume é igual à
energia de distorção acumulada no elemento de volume
quando sob condição de carregamento uniaxial.
Representação Gráfica 3D da
Eq. de Von Mises
Assim, quando a tensão equivalente de Von Mises exceder o limite de escoamento
do material, escoamento generalizado irá ocorrerá.
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Comportamento Cíclico dos Materiais Metálicos
Modelo de Endurecimento do Material
Critério de Escoamento de Mises:
Observe que, se o estado de tensão estiver no interior
do cilindro, não ocorrerá escoamento. Isto significa
que,
se
o
material
se
encontra
sob
pressão
hidrostática (σ1 = σ2 = σ3), não haverá pressão
hidrostática que causará escoamento.
Representação Gráfica 3D da
Eq. de Von Mises
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Comportamento Cíclico dos Materiais Metálicos
Modelo de Endurecimento do Material
Regras de Endurecimento:
Outra maneira de representar a Eq. de Mises é utilizando o eixo que define a
condição σ1 = σ2 = σ3.
Uma regra de endurecimento descreve como as
mudanças na superfície de rendimento (tamanho,
centro, forma) como resultado da deformação plástica.
A regra endurecimento determina quando o material irá
produzir de novo, se o carregamento é continuada ou
revertida.
Plastificação
Superfície de escoamento após o carregamento
Elástico
Superfície de escoamento inicial
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Comportamento Cíclico dos Materiais Metálicos
Modelo de Endurecimento do Material
Regras de Endurecimento:
Existem duas regras básicas de endurecimento que induz a modificação da
superfície de escoamento
Endurecimento Cinemático:
A
superfície
de escoamento
permanece
constante em tamanho e se translada na direção
de escoamento.
Endurecimento isotrópico:
A superfície de escoamento se expande de
maneira uniforme em todas as direções com
o fluxo de plástico.
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Comportamento Cíclico dos Materiais Metálicos
Modelo de Endurecimento do Material
Regras de Endurecimento – Endurecimento Cinemático
A maioria dos metais apresentam um comportamento endurecimento cinemático
para pequenas deformações cíclicas
Após o material ser solicitado a um
nível de tensão superior à tensão de
escoamento do material, y, ele só
voltará a sofrer escoamento em
compressão quando a variação do
nível de tensão exceder 2σy. (Efeito
Bauschinger).
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Comportamento Cíclico dos Materiais Metálicos
Modelo de Endurecimento do Material
Regras de Endurecimento – Endurecimento Isotrópico
O endurecimento isotrópico é frequentemente usado em grandes deformações ou
simulações de carga proporcionais. Normalmente, não é aplicável para a carga cíclica
A
condição
de
endurecimento
isotrópico a superfície de escoamento
se expande uniformemente durante o
fluxo de plástico. Note-se que o
subsequente
escoamento
em
compressão é igual à maior tensão
atingida durante a fase de tração.
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Comportamento Cíclico dos Materiais Metálicos
Efeito da Aplicação de Esforços de Forma Ciclica
Material Endureceu
Material Endureceu
Deformação Total
t = e + p
Deformação Plástica
Material Endureceu
Material
Amoleceu
Deformação Elástica
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Comportamento Cíclico dos Materiais Metálicos
Relação Deformação Vida – -N
O comportamento cíclico pode ser descrito nos termos dos
componentes do laço de histerese, para condições de
controle por deformação, em um ciclo totalmente reverso.
D
2
D e

2
D p
2
D e

2
 'f
E

D p
2
(2 N )
b
f
  (2 N f )
c
'
f
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
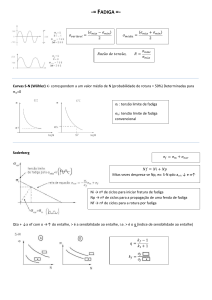
Relação Deformação Vida (-N)
Linha Elástica:
• Basquin:
D  f
(2 N f )b   'f (2 N f )c

2
E
'
 'f
b
D
b
a 
  'f (2 N f )
2
= Coeficiente de Resistência à fadiga
= Expoente de resistência à fadiga
Linha Plástica:
D p
2
  'f (2 N f )
c
• Coffin-Manson:
 'f
c
= Coeficiente de ductilidade de fadiga
= expoente de ductilidade de fadiga
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Relação Deformação Vida (-N)
Estimativa das Propriedades cíclicas dos materiais
 'f= Coeficiente de Resistência à fadiga: É a tensão verdadeira necessária para causar fratura
na 1ª reversão.
 'f   f
b = Expoente de resistência à fadiga: É a inclinação da linha elástica. Varia de -0,14
(materiais moles) a –0,06 (materiais duros)
 'f = Coeficiente de ductilidade de fadiga: É a deformação verdadeira necessária para causar
fratura na 1ª reversão.
c = expoente de ductilidade de fadiga:
1
  'f  n '
'
 f  0,002 ' 
 Se 
100


 'f   f  ln 

 100  % RA 
É a inclinação da linha plástica. Varia de -0,5 a –0,07
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Método das Deformações Locais
É um enfoque adotado para análise de
componentes entalhados quando as
tensões locais na raiz do entalhe
excedem a tensão de escoamento do
material.
Sy
DP
Assume que o comportamento à fadiga de
um componente entalhado é o mesmo de
um corpo de prova não-entalhado,
submetido às mesmas condições de
tensão e deformação que existem na raiz
do entalhe.
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Método das Deformações Locais
Construção da Curva Tensão Deformação Cíclica

D
Hipótese de Masing (1926)
Assumindo que os ciclos de
histerese
alcançaram
a
condição estável, conforme
comportamento ilustrado na
figura a lado, em que a curva
interior é a curva de tensãodeformação cíclica,  = f().
Já a curva exterior descreve
um
ciclo
de
histerese
fechado é expressa pela
relação: D = f(D),
E


 
 
E  K' 
D
1
n'

D
D 
D
D
 D 
 2

E
2
K
'


1
n'
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Método das Deformações Locais
Construção da Curva Tensão Deformação Cíclica
Hipótese de Masing (1926)
O assim chamado comportamento
Masing, descritos pelas fórmulas
no slide anterior, pode ser
utilizado para construir curvas
de histerese fechadas, de
qualquer tipo e localização, tal
como ilustrado a seguir:
F(t)
Al 7050 – T7451
Análise estatística
H'
n'
620,65
0,069
Desvio padrão
7,84
0,0021
C. V. (%)
1,26
3,10
Média
E = 70000 MPa
F(t)
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Método das Deformações Locais
Construção da Curva Tensão Deformação Cíclica
Hipótese de Masing (1926)
Vamos aplicar a primeira
reversão de carga até 500
MPa de tensão. No início
desse processo a eq. que
rege a evolução da curva -
é

 
   
E  K' 
1
n'

600
(?, 500)
(1)
400
200

0
-200
-400
-600
-0.1
-0.08
-0.06
-0.04
-0.02
0
0.02
0.04
0.06
0.08
0.1
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Método das Deformações Locais
Construção da Curva Tensão Deformação Cíclica
Hipótese de Masing (1926)
No
final
do
processo
de
carregamento, a curva  para no
ponto (51.115mStrain, 500 MPa).
Para a construção do ramo da
curva entre 500 e -400 MPa,
mudaremos a origem do sistema
para o (51.115mStrain, 500 MPa) e
recorreremos a função padrão
D 
D
 D 
 2

E
2
K
'


e desenvolveremos
incremental da curva
1
n'
D
600
((1), (1)) = (51115, 500)
(1)
400
200
D
0
-200
-400
-600
a
-0.1
evolução
-0.08
-0.06
-0.04
-0.02
0
0.02
0.04
0.06
0.08
0.1
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Método das Deformações Locais
Construção da Curva Tensão Deformação Cíclica
Hipótese de Masing (1926)
No
final
do
processo
de
carregamento, a curva  para no
ponto (51.115mStrain, 500 MPa).
Para a construção do ramo da
curva entre 500 e -400 MPa,
mudaremos a origem do sistema
para o (51.115mStrain, 500 MPa) e
recorreremos a função padrão
D 
D
 D 
 2

E
2
K
'


e desenvolveremos
incremental da curva
1
n'
600
400
D
Final da Primeira Reversão:
ε 1 : 51115
((1), (1)) = (51115, 500)
(1)
σ1 : 500 MPa
200
D
0
-200
-400
-600
a
-0.1
evolução
-0.08
-0.06
-0.04
-0.02
0
0.02
0.04
0.06
0.08
0.1
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Método das Deformações Locais
Construção da Curva Tensão Deformação Cíclica
Hipótese de Masing (1926)
No
final
do
processo
de
carregamento, a curva  para no
ponto (51.115mStrain, 500 MPa).
Para a construção do ramo da
curva entre 500 e -400 MPa,
mudaremos a origem do sistema
para o (51.115mStrain, 500 MPa) e
recorreremos a função padrão
D
 D 
D 
 2

E
2
K
'


e desenvolveremos
incremental da curva
1
n'
((1), (1)) = (51115, 500)
600
(1)
400
(2)
200
0
-200
-400
-600
-0.1
a
evolução
-0.08
-0.06
-0.04
-0.02
0
0.02
0.04
0.06
0.08
0.
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Método das Deformações Locais
Construção da Curva Tensão Deformação Cíclica
Hipótese de Masing (1926)
No
final
do
processo
de
carregamento, a curva  para no 400
ponto (51.115mStrain, 500 MPa).
200
Para a construção do ramo da
curva entre 500 e -400 MPa, 0
mudaremos a origem do sistema
-200
para o (51.115mStrain, 500 MPa) e
recorreremos a função padrão
-400
600
D 
D
 D 
 2

E
2
K
'


e desenvolveremos
incremental da curva
1
n'
Final da Primeira Reversão:
((1), (1)) = (51115, 500)
ε 1 : 51115
(1)
σ1 : 500 MPa
(2)
D
D
((21), (21)) = (50401, 450)
-600
a
-0.1
evolução
-0.05
0
0.05
0.1
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Método das Deformações Locais
Construção da Curva Tensão Deformação Cíclica
Hipótese de Masing (1926)
No
final
do
processo
de
carregamento, a curva  para no
ponto (51.115mStrain, 500 MPa).
Para a construção do ramo da
curva entre 500 e -400 MPa,
mudaremos a origem do sistema
para o (51.115mStrain, 500 MPa) e
recorreremos a função padrão
D 
D
 D 
 2

E
2
K
'


e desenvolveremos
incremental da curva
1
n'
600
Final da Primeira Reversão:
((1), (1)) = (51115, 500)
ε 1 : 51115
400
(1)
σ1 : 500 MPa
(2)
D
D
((22), (22)) = (48972, 350)
200
0
-200
-400
-600
a
-0.1
evolução
-0.05
0
0.05
0.1
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Método das Deformações Locais
Construção da Curva Tensão Deformação Cíclica
600
((1), (1)) = (51115, 500)
Hipótese de Masing (1926)
Ao alcançar o nível de -400 MPa,
a deformação resultante será
igual a 19142 mstrain. Voltaremos
então a carregar a peça até a
tensão alcançar 450 MPa.
Para a construção desse ramo da
curva relacionado a essa reversão,
mudaremos a origem do sistema
para o (19142mStrain, -400 MPa)
e desenvolveremos a evolução
incremental usando a função
padrão D  D  2 D 
1
n'
E
 2K ' 
400
(1)
(2)
200
D
0
-200
-400
D
((2f), (2f)) = (19142, -400)
-600
-0.1
-0.08
-0.06
-0.04
-0.02
0
0.02
0.04
0.06
0.08
0.1
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Método das Deformações Locais
Construção da Curva Tensão Deformação Cíclica
Hipótese de Masing (1926)
600
Ao alcançar o nível de -400 MPa, 400
a deformação resultante será
igual a 19142 mstrain. Voltaremos 200
então a carregar a peça até a 0
tensão alcançar 450 MPa.
Para a construção do ramo da -200
curva relacionado a essa reversão, -400
mudaremos a origem do sistema
para o (19142mStrain, -400 MPa) -600
e desenvolveremos a evolução -0.1
incremental usando a função
padrão D  D  2 D 
1
n'
E
 2K ' 
((3f), (3f)) = (39556, 450)
(1)
(3)
D
(2)
((2f), (2f)) = (19142, -400)
-0.05
0
0.05
D
0.1
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Método das Deformações Locais
Construção da Curva Tensão Deformação Cíclica
Hipótese de Masing (1926)
600
Ao alcançar o nível de 450 MPa, a 400
deformação resultante será igual
a 39556 mstrain. Voltaremos 200
então a descarregar a peça até a 0
tensão alcançar -350 MPa.
Para a construção do ramo da -200
curva relacionado a essa reversão, -400
mudaremos a origem do sistema
para o (39559mStrain, 450 MPa) -600
e desenvolveremos a evolução -0.1
incremental usando a função
padrão D  D  2 D 
1
n'
E
 2K ' 
((3f), (3f)) = (39556, 450)
(1)
(3)
D
(2)
((2f), (2f)) = (19142, -400)
-0.05
0
0.05
D
0.1
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Método das Deformações Locais
Construção da Curva Tensão Deformação Cíclica
Hipótese de Masing (1926)
600
Ao alcançar o nível de 450 MPa, a 400
deformação resultante será igual
a 39556 mstrain. Voltaremos 200
então a descarregar a peça até a 0
tensão alcançar -350 MPa.
Para a construção do ramo da -200
curva relacionado a essa reversão, -400
mudaremos a origem do sistema
para o (39559mStrain, 450 MPa) -600
e desenvolveremos a evolução -0.1
incremental usando a função
padrão D  D  2 D 
1
n'
E
 2K ' 
D
((3f), (3f)) = (39556, 450)
(1)
(3)
(2)
D
((2f), (2f)) = (19142, -400)
-0.05
0
0.05
0.1
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Método das Deformações Locais
Construção da Curva Tensão Deformação Cíclica
Hipótese de Masing (1926)
600
Ao alcançar o nível de -350 MPa, 400
a deformação resultante será
igual a 24692 mstrain. Voltaremos 200
então a carregar a peça até a 0
tensão alcançar 475 MPa.
Para a construção do ramo da -200
curva relacionado a essa reversão, -400
mudaremos a origem do sistema
para o (24692mStrain, -350 MPa) -600
e desenvolveremos a evolução -0.1
incremental usando a função
padrão D  D  2 D 
1
n'
E
 2K ' 
D
((3f), (3f)) = (39556, 450)
(1)
(3)
(2)
D
(4)
((4f), (4f)) = (24692, -350)
((2f), (2f)) = (19142, -400)
-0.08
-0.06
-0.04
-0.02
0
0.02
0.04
0.06
0.08
0.1
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Método das Deformações Locais
Construção da Curva Tensão Deformação Cíclica
Hipótese de Masing (1926)
600
Ao alcançar o nível de -350 MPa, 400
a deformação resultante será
igual a 24692 mstrain. Voltaremos 200
então a carregar a peça até a 0
tensão alcançar 475 MPa.
Para a construção do ramo da -200
curva relacionado a essa reversão, -400
mudaremos a origem do sistema
para o (24692mStrain, -350 MPa) -600
e desenvolveremos a evolução -0.1
incremental usando a função
padrão D  D  2 D 
1
n'
E
 2K ' 
((3f), (3f)) = (39556, 450)
(1)
(3)
D
(2)
(4)
((4f), (4f)) = (24692, -350)
D
((2f), (2f)) = (19142, -400)
-0.08
-0.06
-0.04
-0.02
0
0.02
0.04
0.06
0.08
0.1
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Método das Deformações Locais
Construção da Curva Tensão Deformação Cíclica
Hipótese de Masing (1926)
600
Ao alcançar o nível de -350 MPa, 400
a deformação resultante será
igual a 24692 mstrain. Voltaremos 200
então a carregar a peça até a 0
tensão alcançar 475 MPa.
Para a construção do ramo da -200
curva relacionado a essa reversão, -400
mudaremos a origem do sistema
para o (24692mStrain, -350 MPa) -600
e desenvolveremos a evolução -0.1
incremental usando a função
padrão D  D  2 D 
1
n'
E
 2K ' 
((5f), (5f)) = (41844, 475)
((3f), (3f)) = (39556, 450)
(1)
(3)
(5)
D
(2)
(4)
((4f), (4f)) = (24692, -350)
D
((2f), (2f)) = (19142, -400)
-0.08
-0.06
-0.04
-0.02
0
0.02
0.04
0.06
0.08
0.1
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Método das Deformações Locais
Construção da Curva Tensão Deformação Cíclica
Hipótese de Masing (1926)
Para alcançar o nível de 475 MPa,
a reversão (5) cruzou a reversão
(3). Em materias que podem ser
representados pela a hipótese de
Masing, esse cruzamento não
existe.
Nesses materiais, quando uma
reversão encontra uma já iniciada,
a tendência da curva é seguir o
caminho da reversão já iniciada
500
480
460
440
420
400
380
360
0.034
0.036
0.038
0.04
0.042
0.044
0.046
0.048
0.05
0.052
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Método das Deformações Locais
Construção da Curva Tensão Deformação Cíclica
Hipótese de Masing (1926)
Para alcançar o nível de 475 MPa, a
reversão (5) cruzou a reversão (3).
Nas curvas  de materiais reais
não se observa esse cruzamento
não existe.
Nesses materiais, quando uma
reversão (5) encontra outra já
iniciada (3), a tendência da
reversão mais recente (5) é
acompanhar o caminho da reversão
já iniciada (3).
((3f), (3f)) = (39556, 450)
400
300
200
(3)
(5)
100
(4)
0
(2)
-100
-200
-300
0.02
0.025
0.03
0.035
0.04
0.045
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Método das Deformações Locais
Construção da Curva Tensão Deformação Cíclica
Hipótese de Masing (1926)
Para simular esse comportamento,
procede-se a evolução da reversão
do seu ponto de início [5i] até o
ponto de interseção entre as
reversões [5f] coordenada global
(39556,450).
500
[5f]
400
((5f), (5f)) = (44300, 475)
((3f), (3f)) = (39556, 450)
300
200
(2)
(3)
100
0
D
D
(5)
(4)
-100
A partir desse ponto, transfere a
-300
origem e calcula-se os pontos
-400
pertencentes a essa reversão
-500
específica do intercessão até o seu 0.01 0.015 0.02
final, caso a curva não intercepte
outra reversão que já tenha sido desenvolvida
-200
[5i]
D
0.025
0.03
0.035
D
0.04
0.045
0.05
0.055
0.06
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Método das Deformações Locais
Construção da Curva Tensão Deformação Cíclica
Como Identificar o Comportamento tipo Masing ?
Um material exibe comportamento tipo Masing se os ramos, ascendentes e
descendentes, dos ciclos de histerese puderem ser descritos através da
curva cíclica do material, multiplicada por um fator de escala de 2:
Curva cíclica do material
comportamento tipo Masing
Comportamento tipo
não-Masing
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Método das Deformações Locais
Construção da Curva Tensão Deformação Cíclica
Comportamento da Liga Al 7050-T745 (tipo não-Masing)
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Método das Deformações Locais
Construção da Curva Tensão Deformação Cíclica
Exercício
Construir a curva de histerese da liga Al 7050 – T7451, assumindo
hipoteticamente que essa liga possua comportamento Masing e que seja
solicitada pela seguinte história de tensões:
0; 500; -400; 450; -350; 475; -400; 510; -125; 520 [MPa]
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Método das Deformações Locais
Construção da Curva Tensão Deformação Cíclica
Respostas
Análise de Fadiga segundo o Método Deformação-Vida (e-N) – Módulo 2.3
Método das Deformações Locais
Construção da Curva Tensão Deformação Cíclica
Respostas