Visualização da tensão devido a flexão

Visualização da tensão normal
devida a flexão

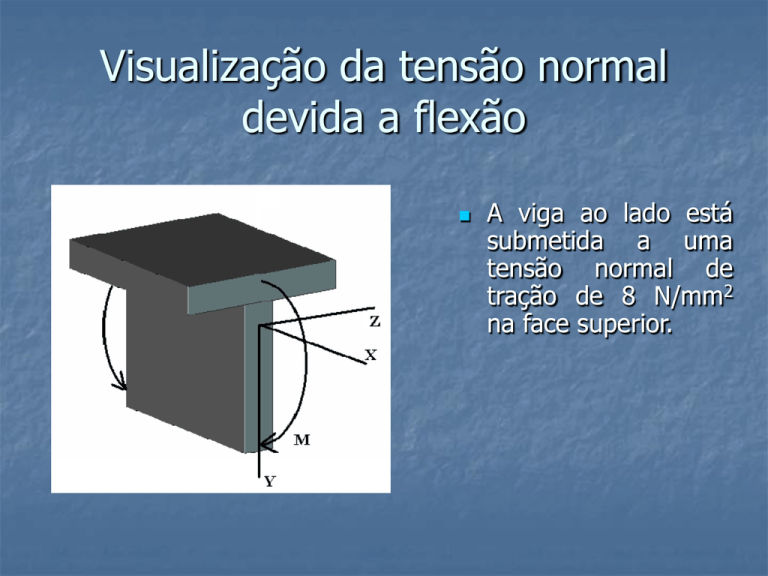
A viga ao lado está
submetida a uma
tensão normal de
tração de 8 N/mm2
na face superior.


Para esse momento,
tem-se tensões normais
de tração na região
acima
da
superfície
neutra
(passa
pelo
centróide da seção).
E tensões normais de
compressão na região
abaixo da superfície
neutra.

Determinar a força resultante das tensões normais em
em cada parte numerada da seção transversal.
Sem usar a fórmula de tensão normal, determinar o
valor do momento fletor na seção.


Divida a distribuição
de tensão em porção
uniforme e em porção
distribuída linearmente
F1,unif  4,44  50  300  6,67  10 4 N
F1,unif  66,7kN
1
 8  4,44  50  300  2,67  10 4 N
2
 26,7kN
F1,lin 
F1,lin

Divida a distribuição de
tensão
em
porção
uniforme e em porção
distribuída linearmente
F2,unif  0 N .
1
 4,44  0,00   50  62,5  6,94  10 3 N
2
 6,94kN
F2,lin 
F2,lin

Divida a distribuição
de tensão em porção
uniforme e em porção
distribuída linearmente
F3,unif  0 N .
1
 16,89  0,00  50  237,5  1,003  10 5 N
2
 100,3kN
F3,lin 
F3,lin
-



Note que a soma das forças é zero, ou seja a soma das forças de
compressão é igual à soma das forças de tração.
Para calcular o momento de força resultante em cada região com
relação à linha neutra (eixo z) tem-se que determinar o ponto de
aplicação da resultante. O momento é o produto do valor da força
pela distância do seu ponto de aplicação à linha neutra.
Somando todos os momentos das forças com relação à linha neutra,
tem-se o momento fletor na seção que, no caso visto, é de 24563
kN.mm.