O condensador

CONDENSADOR
O condensador (ou o capacitor) é um elemento importante no circuito elétrico.
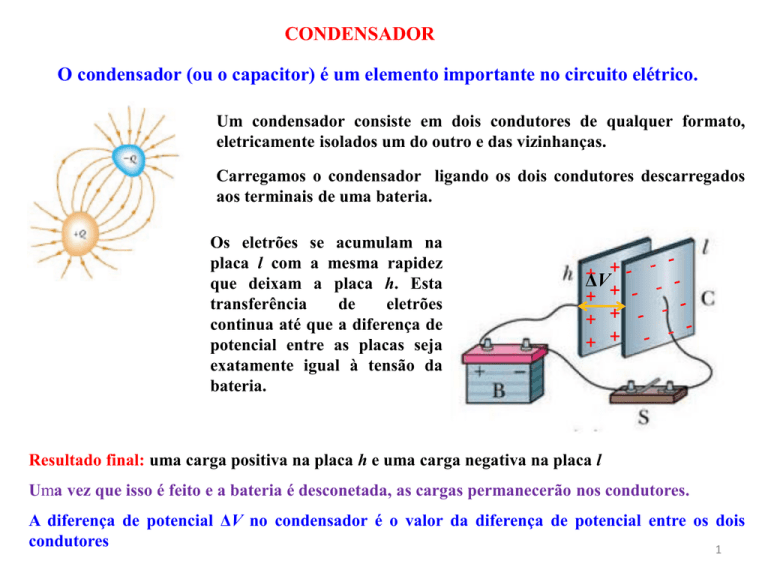
Um condensador consiste em dois condutores de qualquer formato,
eletricamente isolados um do outro e das vizinhanças.
Carregamos o condensador ligando os dois condutores descarregados
aos terminais de uma bateria.
Os eletrões se acumulam na
placa l com a mesma rapidez
que deixam a placa h. Esta
transferência
de
eletrões
continua até que a diferença de
potencial entre as placas seja
exatamente igual à tensão da
bateria.
+
+
ΔV
+ +
+ +
+ +
Resultado final: uma carga positiva na placa h e uma carga negativa na placa l
Uma vez que isso é feito e a bateria é desconetada, as cargas permanecerão nos condutores.
A diferença de potencial ΔV no condensador é o valor da diferença de potencial entre os dois
condutores
1
CAPACIDADE
Quando um condensador está carregado, suas placas possuem
cargas iguais e opostas, + Q e -Q, mas nos referimos à carga do
condensador como sendo Q.
A carga e a diferença de potencial para um condensador são
proporcionais, e a relação entre elas pode ser escrita como
ΔV
Q  CV
A constante de proporcionalidade C é denominada de capacidade do condensador
C representa uma medida da quantidade de carga que pode ser armazenada no condensador ou
seja a sua capacidade de armazenamento.
C
Q
V
 por definição, capacidade é sempre uma grandeza positiva
A unidade da capacidade no SI é o farad (F).
1F = 1 C / V
O farad é uma unidade muito grande de capacidade. Na prática, os dispositivos típicos têm
12
6
capacidades variando de microfarad ( 10 F) a picofarad ( 10
F)
Símbolo do condensador 
2
A capacidade de um dispositivo depende do arranjo geométrico dos condutores
Exemplo
Determine a capacidade dum condensador de placas paralelas sabendo que A  2.00  104 m2 e a
separação entre as placas d=1.00 mm . O campo elétrico entre as placas é
E
 =Q/A

0
 densidade superficial de carga
SOLUÇÃO:
E

Q

0 0 A
Como o campo elétrico é uniforme, a diferença de potencial no
condensador é
V  Ed 
Qd
0 A
A capacidade é
Q
Q

C

V Qd /  0 A
C
0 A
d

3
ENERGIA ACUMULADA NUM CONDENSADOR CARREGADO
Para calcular a energia armazenada no condensador, imagine carregar o condensador de uma
maneira diferente mas que produz o mesmo resultado.
Considere que um agente externo captura pequenas quantidades de carga e as transfere duma
placa para a outra para a outra.
Suponha que q é a carga no condensador em algum instante durante o processo de carregamento.
dq
+
+
+
+
+
+
-
q
q
Nesse instante, a diferença de potencial no condensador é
V 
q
C
O trabalho necessário para transferir um incremento de carga dq da
placa de carga -q para a placa de carga q (que está no potencial mais
elevado) é
q
dW  Vdq  dq
C
O trabalho total necessário para carregar o condensador de q=0 até
a carga final Q
Q
q
Q2
W   dq 
C
2C
0
4
O trabalho feito pelo agente externo sobre o sistema ao carregar o condensador aparece como a
energia potencial U, armazenada no condensador: W=U
Na realidade essa energia não é devida ao trabalho mecânico feito por um agente externo para
deslocar carga de uma placa para a outra, mas é devida à transformação da energia química na
bateria.
Substituímos em W
Q  CV 
Q2 1
2
U
 C V 
2C 2
Esse resultado aplica-se a qualquer condensador, independentemente de sua geometria.
Para um condensador de placas paralelas, a diferença de potencial se relaciona ao campo elétrico
pela relação V = Ed e
C  0 A / d
A energia potencial é
1 A
1
2
U   0 Ed    0 Ad E 2
2 d 
2
Como o volume = Ad e a energia por unidade de volume u = U/Ad denominada densidade de
energia, é
1
u  0E 2
2
 expressão válida para qualquer condensador
5
CONDENSADORES COM DIELÉTRICOS
Um dielétrico é um material não condutor como borracha, vidro ou papel encerado.
Michael Faraday descobriu que quando um material dielétrico é introduzido entre as placas de um
condensador, preenchendo completamente o espaço entre as placas 
a capacidade aumenta de um factor numérico κ, que Faraday chamou de constante dielétrica.
V 
V0

como V < V0 , vemos que  > 1
C
Q
Q
Q



V V0 / 
V0
C  C0
C0 
Q
V0
6
Para um condensador de placas paralelas
C0 
0 A
d
Podemos expressar a capacidade quando o condensador for
preenchido com um dielétrico como
C 
0 A
d
A partir desse resultado, parece que a capacidade poderia se
tornar grande diminuindo-se d
Na prática, o valor mais baixo de d é limitado pela descarga
elétrica que pode ocorrer pelo meio dielétrico que separa as
placas
Para qualquer d a tensão máxima aplicada a um condensador,
sem causar uma descarga, depende da rigidez dielétrica (campo
elétrico máximo) do dielétrico
Para o ar seco = 3 106 V/m
Se o campo elétrico no meio exceder a rigidez dielétrica, as propriedades de isolamento são
rompidas e o meio passa a ser condutor.
A maioria dos materiais isoladores tem rigidez dielétrica e constante dielétrica maiores que as do
ar
7
Vemos que um dielétrico fornece as seguintes vantagens:
• Aumenta capacidade de um condensador.
• Aumenta a tensão máxima de operação de um condensador.
• Pode fornecer sustentação mecânica entre as placas condutoras.
Efeitos do dielétrico
Moléculas polares orientadas aleatoriamente
Moléculas polares alinhadas com o campo elétrico


E0  campo elétrico entre as placas (sem o dielétrico )


E'  campo elétrico induzido (oposto a E0 )


E  campo elétrico resultante
O campo elétrico, e a tensão entre as placas são reduzidas e como a
carga nas placas é armazenada a uma diferença de potencial menor, a
capacidade aumenta porque
C
Q
V
8
Exemplo 1: ATMOSFERA COMO UM CONDENSADOR
Supomos que a superfície da Terra é uma placa e a carga positiva no ar (espalhada por toda a
atmosfera) é a outra placa. Os modelos da atmosfera mostram que a altura efetiva da placa é de
aproximadamente 5 km da superfície da Terra. Determinar a capacidade do condensador
atmosférico.
h
Placa positiva
(cargas na atmosfera)
Placa negativa
(superfície da Terra )
Campo elétrico num exterior de uma
distribuição de carga com simetria
esférica é semelhante ao de uma carga
pontual:
Q
E  ke 2
r
r
P
Cálculo do potencial elétrico
r
r
 
dr
Q
VP    E  ds    Er dr  keQ  2  ke
r
r



P
Q é a carga na superfície
9
Vh
h
VT
V
V  VT  Vh 
1
Q
1
Q


40 RT 40 RT  h
onde RT é o raio da Terra e h = 5 km. Por essa expressão, podemos calcular a capacidade do
condensador atmosférico:
=
1000 m
1 km
Este valor é extremamente grande quando comparado com os Picofarads e microfarads que são
os valores típicos para condensadores em circuitos elétricos, especialmente para um condensador
que tem placas que estão a 5 km uma da outra!
10
Exemplo 2: Supor que a Terra e uma camada de nuvens a 800 m acima da
Terra são as placas de um condensador. a) Calcule a capacidade se a camada
de nuvens tem uma área de 1.0 km2 . b) Se um campo elétrico de 3106 N/C faz
o ar se romper e conduzir eletricidade (ou seja causa raios), qual é a carga
máxima que a nuvem pode suportar ?
a) Cálculo de C:
0 A
8.85 10 12  (103 ) 2
C

800
d
 1.10625 108  11109  11 nF
b) Cálculo de Q:
Q
C
 Q  CV  CEd
V
 1110 9  3 106  800  26.4 C  26 C
11