AULA 25 - LEST

Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
Variação de Entropia do Sistema Durante um
Processo Irreversível
Aplicando a desigualdade de Clausius:
2
S 2  S1 

1
Q
dS 
Q
T
(1a)
(1b)
T
• Esta equação demonstra a influência da irreversibilidade na
entropia de um sistema.
• Se durante a transferência da quantidade de calor Q para o
sistema à temperatura T ocorrerem efeitos irreversíveis, a variação
da entropia será maior do que a do processo reversível.
• As irreversibilidades influenciam no sentido de aumentar a entropia
do sistema.
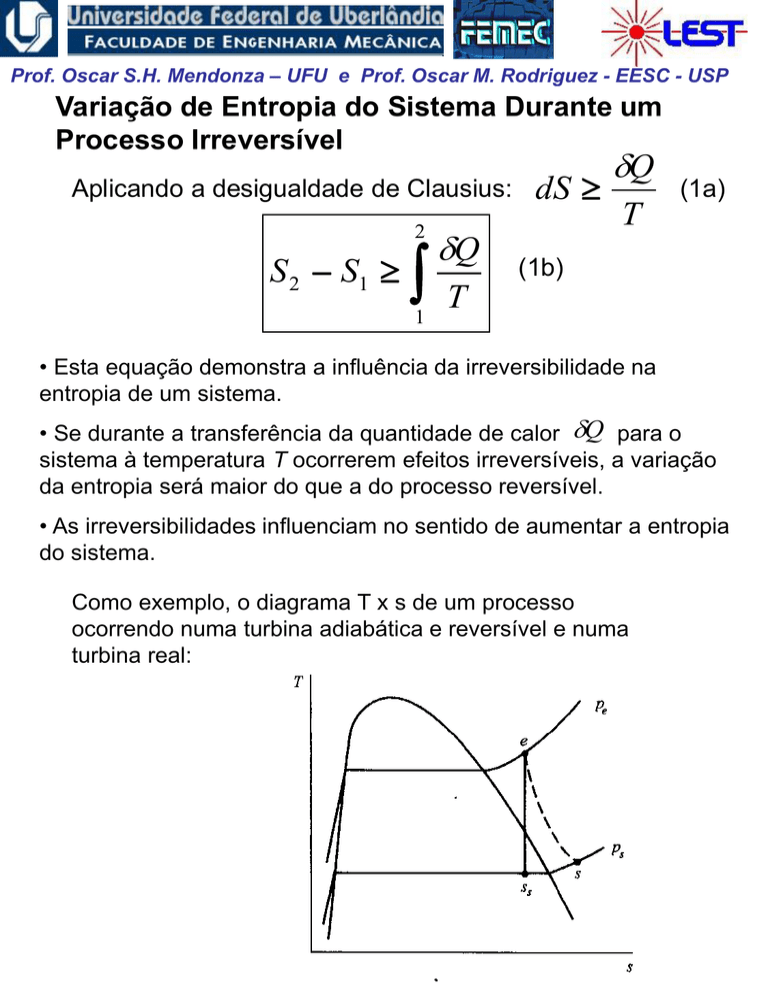
Como exemplo, o diagrama T x s de um processo
ocorrendo numa turbina adiabática e reversível e numa
turbina real:
Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
Geração de Entropia (trabalho perdido)
De modo a obter uma expressão para a variação da
entropia para um processo irreversível que envolva uma
igualdade e não uma desigualdade (Eq. 1a), podemos
escrever:
dS 
onde:
Q
T
2
 S ger ou S 

Q
1
S ger  0
T
 1S 2, ger
= para processos reversíveis
> para processos irreversíveis
Da Eq. (2), temos que a transferência de calor em
processo irreversível é menor do que aquela do
processo reversível:
Qirr  TdS  TS ger
Utilizando a 1a lei da termodinâmica, temos que o
trabalho em processo irreversível também é menor
do que aquele que o do processo reversível:
Wirr  pdV  TS ger
Trabalho perdido
(2)
Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
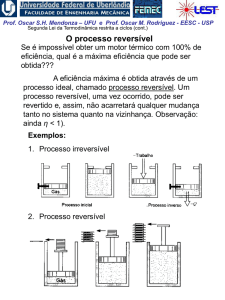
Observações quanto à geração de entropia:
1. Há 2 formas de aumentar a entropia de um sistema:
1. Transferência de calor para o sistema
2. O sistema realizar um processo irreversível
2. Há apenas uma forma possível de diminuir a entropia
de uma sistema: transferência de calor do sistema
(geração de entropia não pode ser negativa)
3. Para um processo adiabático, Q  0 , o incremento de
entropia é sempre associado às irreversibilidades.
4. Considerando os gráficos p x V e T x S, a área abaixo
das linhas relacionadas aos processos irreversíveis
nunca representarão trabalho ou calor (linhas
pontilhadas).
Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
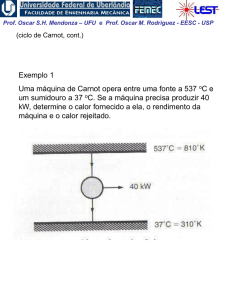
Exemplo 3:
Água inicialmente como líquido saturado a 100oC está
contida num conjunto êmbolo-cilindro. A água realiza um
processo ao estado correspondente de vapor saturado,
durante o qual o êmbolo move-se livremente no cilindro.
Não há transferência de calor com a vizinhança. Se a
mudança de estado ocorre devido a ação de um agitador,
(a) determine o trabalho por unidade de massa, ambos
em kJ / kg; e (b) a quantidade de entropia produzida por
unidade de massa em kJ / kg K.
Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
Exemplo 4:
Durante uma operação em regime permanente, uma caixa de
transmissão de eixos paralelos recebe 600 kW pelo eixo de alta
velocidade, mas devido a fricção e outras irreversibilidades entrega
apenas 588 kW pelo eixo de baixa velocidade. A caixa de transmissão
é arrefecida na sua superfície externa de acordo com
Q  hATb  To 
onde h é o coeficiente de transferência de calor, A é a área da
superfície externa, Tb é a temperatura uniforme da superfície externa,
e To é a temperatura uniforme da vizinhança distante da vizinhança
imediata da caixa de transmissão. Avalie a taxa de geração de entropia,

, em kW / K,
(a) a caixa de transmissão como o sistema e (b) um
1 S 2para
, ger
sistema maior consistindo da caixa de transmissão e o suficiente de
sua vizinhança para a transferência de calor ocorrer a temperatura To.
Considere h = 0,17 kW / m2 K, A = 1,8 m2 e To = 293 K.
Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
Princípio do Aumento da Entropia
Consideremos agora um universo constituído por um
sistema e o meio:
Temos para o sistema que, da Eq. (1a) :
dS sistema 
Q
T
Para o meio (reversível por definição), temos que:
dS meio
Q

To
geração de
entropia
Portanto a variação líquida de entropia é:
dSuniverso  dS sistema  dS meio
1 1 
 Q  
 T To 
Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
Assim:
1 1 
 dS UNIV   Q   
 T T0 
 Q  T0 
 dS UNIV   1
T0  T

ou:
Como To > T ,
(To / T – 1)
será sempre positivo.
Concluímos que:
dS UNIV  dSsistema  dSmeio  0
ou
dSUNIV  dS sistema  dS meio 
 S
ger
0
Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
Um outra interpretação considera um balanço de
entropia num sistema isolado. Da Eq. (2), temos que:
=0
2
Ssistema isolado 
Q
 T S
1 2, ger
1
ou:
S sistema isolado 1 S 2, ger  0
Esta equação dita a única direção na qual qualquer
processo pode ocorrer
O princípio do aumento da entropia pode ser
considerado como uma afirmação geral quantitativa da
segunda lei da termodinâmica do ponto de vista
macroscópico.
Do ponto de vista microscópico, podemos dizer que os
únicos processos que um sistema isolado pode realizar
são aqueles que aumentam a “desordem” do sistema.
Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
Variação de entropia de um sólido ou líquido
Temos para sólidos e líquidos que:
dh  du  cdT
Da equações de Gibbs:
0
Tds  dh  vdp
dh du c
ds 

 dT
T
T
T
Como mencionado no Cap. 5, podemos considerar
o calor específico constante em muitos processos
que envolvem sólidos ou líquidos; assim:
 T2 
s2  s1  c ln  
 T1 
Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
Exemplo 5:
Uma barra de metal (0,3 kg) inicialmente a 1200 K é
removida de um forno e passa por um processo de
têmpera por imersão em um tanque isolado contendo 9
kg de água inicialmente a 300 K. Ambas substâncias
podem ser modeladas como incompressíveis. Adote
calores específicos constantes cw = 4,2 kJ / kg K e cm =
0,42 kJ / kg K para a água e barra, respectivamente. A
transferência de calor do tanque pode ser desprezada.
Determine (a) a temperatura final de equilíbrio do metal é
da água, em K, e (b) a quantidade de entropia gerada,
em kJ / K.