AULA 12 - LEST

Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
A Energia Interna, Entalpia e Calor Específico de
Gases Perfeitos
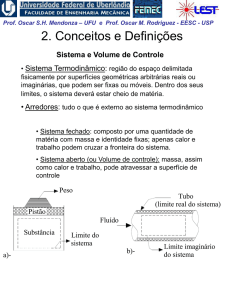
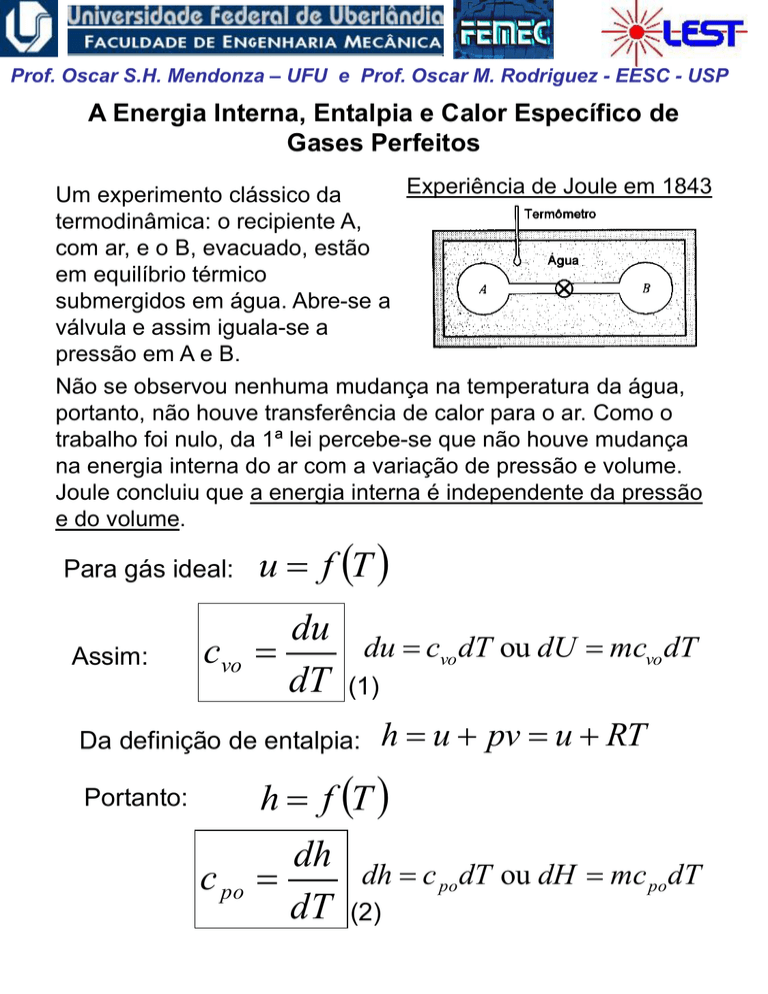
Experiência de Joule em 1843
Um experimento clássico da
termodinâmica: o recipiente A,
com ar, e o B, evacuado, estão
em equilíbrio térmico
submergidos em água. Abre-se a
válvula e assim iguala-se a
pressão em A e B.
Não se observou nenhuma mudança na temperatura da água,
portanto, não houve transferência de calor para o ar. Como o
trabalho foi nulo, da 1ª lei percebe-se que não houve mudança
na energia interna do ar com a variação de pressão e volume.
Joule concluiu que a energia interna é independente da pressão
e do volume.
Para gás ideal:
Assim:
u  f T 
du
cvo 
dT
du  cvo dT ou dU  mcvo dT
(1)
Da definição de entalpia:
h  u  pv  u  RT
h  f T 
Portanto:
c po
dh

dT
dh  c po dT ou dH  mc po dT
(2)
Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
Note acima que qualquer que seja o caminho, a variação de
energia interna e entalpia serão as mesmas. As linhas de
temperatura constante são também linhas de u de h constantes
Os calores específicos a volume constante e pressão
constante são também apenas função da temperatura:
 f T 
cvo

calor específico a volume
cte. a zero pressão
c po

e
 f T 
calor específico a pressão
cte. a zero pressão
Da definição de entalpia e utilizando as eqs. 1 e 2:
dh  du  RdT
c po dT  cvo dT  RdT
c po  cvo  R ou
c po  cvo  R



sempre constante
Precisamos conhecer
apenas um deles!
Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
Quando c po pode ser considerado constante?
Se o calor específico c po é constante, integra-se
diretamente a Eq. (2):
h2  h1 
c po

T2  T1 
uma média,
por exemplo
O valor médio deve ser avaliado no intervalo de
temperatura de aplicação
Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
Entretanto, muitas vezes não podemos supor c po
constante.
Uma possibilidade são as equações ajustadas
empiricamente:
c po  Co  C1  C2 2  C3 3
onde:
[kJ/Kg K]
  T Kelvin  / 1000
Outra possibilidade é a integração dos cálculos da
termodinâmica estatística:
h2  h1  hT2  hT1
(+)
(Sendo a função hT
retirada das tabelas de
gases perfeitos)
Portanto, temos três possibilidades para avaliar c po :
1. Tabelas de gás ideal
2. Equações empíricas
precisão
(-)
3. Calor específico constante
Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
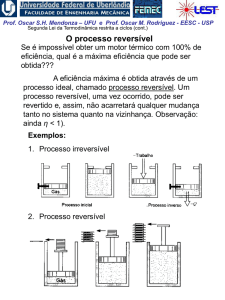
Processo Politrópico de Gás Ideal
Para processo politrópico:
ou
p2  V1 
 
p1  V2 
pV n  cte.
n
Para gás perfeito:
T2  p2 
 
T1  p1 
e
W 
2

1
2
W 

1
 n 1 / n
 V1 
 
 V2 
n 1
mRT2  T1 
pdV 
1 n
V2
pdV  mRT ln
V1
n  1
n  1
Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
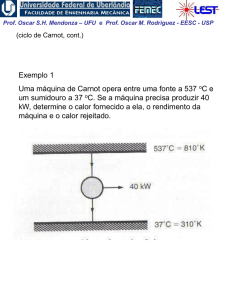
Exemplo 1:
Determine a mudança na entalpia específica, em kJ/kg,
para vapor de água de um estado onde T1 = 400 K e
p1 = 0,1 MPa para um estado onde T2 = 900 K e p1 =
0,5 MPa;
(a) Use a tabela de vapor superaquecido
(b) Integre uma expressão empírica adequada
(c) Repita as partes (a) e (b) para uma pressão final de 60
MPa
Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
Exemplo 2
Dois tanques estão conectados por uma válvula. Um
tanque contém 2 kg de monóxido de carbônico a 77 oC e
70 kPa. O outro tanque contém 8 kg do mesmo gás a 27
oC e 120 kPa. A válvula é aberta e os gases se misturam
enquanto recebem energia por transferência de calor da
vizinhança. A temperatura final de equilíbrio é 42oC.
Utilizando o modelo de gás perfeito, determine:
(a) A pressão final de equilíbrio, em kPa
(b) O calor transferido no processo, em kJ.
Prof. Oscar S.H. Mendonza – UFU e Prof. Oscar M. Rodriguez - EESC - USP
Exemplo 3:
Ar passa por um processo politrópico de compressão
num conjunto pistão-cilindro de p1 = 100 kPa, T1 = 21
oC para p2 = 500 kPa. Empregando o modelo do gás
ideal, determine (a) o trabalho e (b) o calor transferido
por unidade de massa, em kJ/kg, se n = 1,3.