Fontes de campo magnético

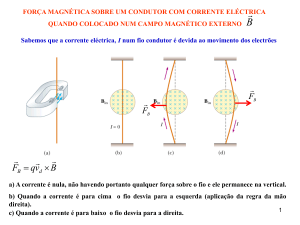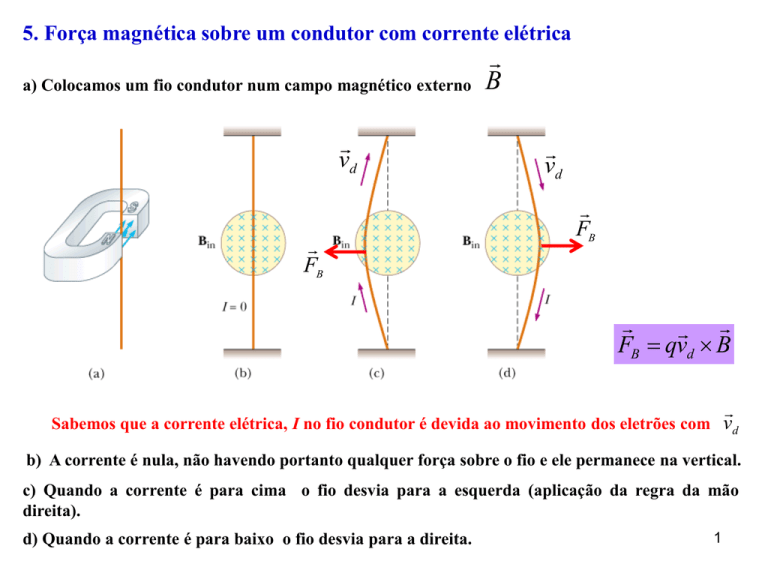
5. Força magnética sobre um condutor com corrente elétrica
a) Colocamos um fio condutor num campo magnético externo

vd

FB

B

vd

FB

 
FB  qvd  B

Sabemos que a corrente elétrica, I no fio condutor é devida ao movimento dos eletrões com vd
b) A corrente é nula, não havendo portanto qualquer força sobre o fio e ele permanece na vertical.
c) Quando a corrente é para cima o fio desvia para a esquerda (aplicação da regra da mão
direita).
d) Quando a corrente é para baixo o fio desvia para a direita.
1
REGRAS DA MÃO DIREITA

 
FB  qvd  B

 
FB  I   B
2

Força magnética sobre um condutor com corrente elétrica num campo magnético externo B
3
FORÇA MAGNÉTICA NUM SEGMENTO DE FIO RETO CONDUZINDO UMA CORRENTE I
E QUE SE ENCONTRA NUM CAMPO MAGNÉTICO UNIFORME
Considerando que
n
N
V
V  A
 número de cargas por volume
 volume do segmento
 N  nV
 número de cargas no fio
Força magnética sobre o fio de comprimento

I  nqvd A
é

 
FB  qvd  B nA

mas




 
FB  I   B

  vetor na direção da corrente
Esta expressão se aplica somente à um fio reto que se encontra num
campo magnético uniforme
4
FORÇA MAGNÉTICA NUM SEGMENTO DE FIO DE FORMA ARBITRÁRIA,
CONDUZINDO UMA CORRENTE I, E QUE SE ENCONTRA NUM CAMPO MAGNÉTICO
UNIFORME
O fio tem uma seção uniforme. A força magnética
sobre um segmento muito pequeno é

 
dFB  Ids  B
A força sobre o fio todo é
b

 
FB  I  ds  B
a
A direção que o campo faz com o vetor

ds
pode variar de ponto a ponto
A relação acima também é válida no caso mais geral em que o condutor tem
uma forma arbitrária e o campo magnético não é uniforme
5
FIO CURVO COM CORRENTE I NUM CAMPO MAGNÉTICO UNIFORME
b

 
FB  I  ds  B
a
'

 b  
FB  I   ds   B
a 
b
A quantidade

 ds
a
representa o vetor soma de todos os pequenos deslocamentos ds ao longo da trajetória
entre a a b, e será igual ao vetor deslocamento
que une os extremos do condutor

'

 
FB  I 'B
6
MOMENTO (TORQUE) SOBRE UMA ESPIRA DE CORRENTE NUM CAMPO MAGNÉTICO
UNIFORME

 
FB  I  ds  B
• O CAMPO MAGNÉTICO É PARALELO AO PLANO DA ESPIRA
b
Lembrando que 
 
ds  B  dsB sin 
a
Para os lados 1 e 3 
 
 
 ds // B  ds  B  0

 FB  0
Para os lados 2 e 4 
F2  F4  IaB sin 90   IaB
Essas duas forças provocam um momento da força
(torque) em relação a O que provoca uma rotação no
sentido horário.
 max
 max
b
b
b
b
 F2  F4  IaB   IaB  
2
2
2
2
 IaB b
A área da espira é
A  ab
 max  IAB
7
• O CAMPO MAGNÉTICO FAZ UM ÂNGULO COM O PLANO DA ESPIRA

A  o vetor área é perpendicu lar ao plano da espira

F2
3
2
4
b
2
2
1
I
b
sin 
2
I
F1   F3  F1  F3  0 e
b
2
4
b
2

F4
F2  F4  IaB
b
2
b
2
  F2 sin   F4 sin   IaB sin   IaB sin   IabB sin  
A área da espira é
A  ab

  IAB sin 
 
  IA  B

8
MOMENTO DE DIPOLO MAGNÉTICO (OU MOMENTO MAGNÉTICO):

  IA

Momento da força (torque) sobre uma espira de
corrente pode ser escrito como

  B


Para uma bobine com N espiras

  N  B


Energia potencial da espira
 
U    B
9
Exemplo: Num enrolamento quadrado de 12 voltas, de lado igual a 40 cm, passa uma
corrente de 3A. O enrolamento repousa no plano xy na presença de um campo
magnético uniforme:



B  0.3 ex  0.4 ez
Determine:
a) O momento dipolo magnético do enrolamento;
b) O momento da força exercido sobre o
enrolamento;
c) A energia potencial do enrolamento.
Resolução




a)   IA  NiA ez  12  3 A  0.40 m2ez  5.76 A m2 ez
 




b)   B  5.76 A m2ez  (0.3 ex  0.4 ez )  1.73 N m ey
 



c) U    B  5.76 A m2ez  (0.3 ex  0.4 ez )  2.30 J

10
EFEITO HALL
O efeito de Hall encontra importantes aplicações na industria eletrónica.
Ele é usado para determinar diretamente o sinal e o número de portadores de carga por volume
num dado material . Por exemplo em chips semicondutores.
A corrente pode ser devida tanto a portadores positivos que se movem para a direita como a
portadores negativos que se movem para a esquerda.
EH
EH
Se a corrente na tira for de cargas positivas: as cargas se acumulam na superfície superior do
material deixando a parte de baixo da tira com excesso de carga negativa. Esta separação de
cargas gera um campo elétrico.
11
O excesso de cargas positivas e negativas, funciona como um condensador de placas paralelas,
com um campo elétrico conhecido como campo Hall.
No equilíbrio a força elétrica para baixo equilibra com a força magnética para cima
Fe  FB

qvd B  qEH
 e os portadores de carga deslocam-se através da amostra sem desvio
12
qvd B  qEH 
vd 
I
nqA
E H  vd B 

VH 
IB RH IB
VH 

nqt
t
VH  EH d  vd Bd
IBd RH IB

nqA
t
 Diferença de potencial de Hall
A  td
 Coeficiente de Hall:
 área
1
RH 
nq
Medindo-se a ddp de Hall entre os pontos a e c, pode-se determinar o sinal e a densidade
volumétrica (n) dos portadores de carga.
IB
VH 
nqt

n
IB
VH qt
13
Exemplo: Por uma placa de prata com espessura de 1 mm passa uma corrente de 2.5 A numa
região na qual existe campo magnético uniforme de módulo 1.25 T perpendicular à placa. O valor
da tensão Hall medida é de 0.334 V. Calcule:
a) A densidade de portadores.
b) Compare a resposta anterior com a densidade de portadores na prata, que possui
densidade   10 .5 g/cm3 e massa molar M= 107.9 g/mol.
eletrões/c m 3
eletrões/c m 3
Nota 

m
V
e
m
 nº de moles
M

m
nº de moles

VM
volume
14