Força magnética sobre um condutor com corrente eléctrica num

FORÇA MAGNÉTICA SOBRE UM CONDUTOR COM CORRENTE ELÉCTRICA

QUANDO COLOCADO NUM CAMPO MAGNÉTICO EXTERNO
B
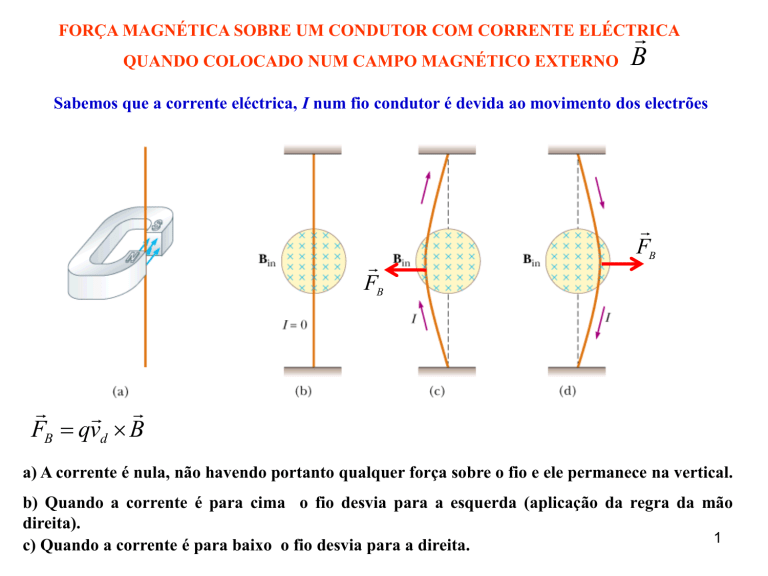
Sabemos que a corrente eléctrica, I num fio condutor é devida ao movimento dos electrões

FB

FB

 
FB  qvd  B
a) A corrente é nula, não havendo portanto qualquer força sobre o fio e ele permanece na vertical.
b) Quando a corrente é para cima o fio desvia para a esquerda (aplicação da regra da mão
direita).
1
c) Quando a corrente é para baixo o fio desvia para a direita.
REGRAS DA MÃO DIREITA

 
FB  qvd  B
ou

 
FB  I   B
2
Força magnética sobre um condutor com corrente eléctrica num campo magnético externo

B
3
FORÇA MAGNÉTICA NUM SEGMENTO DE FIO RECTO CONDUZINDO UMA CORRENTE I E QUE SE
ENCONTRA NUM CAMPO MAGNÉTICO UNIFORME
Considerando que
n
N
V
V  A
 número de cargas por volume
 volume do segmento
 N  nV
 número de cargas no fio
Força magnética sobre o fio de comprimento


mas
I  nqvd A
é


 
FB  qvd  B nA


 
FB  I   B

  vector na direcção da corrente
Esta expressão se aplica somente à um fio recto que se encontra num campo magnético uniforme
4
FORÇA MAGNÉTICA NUM SEGMENTO DE FIO DE FORMA ARBITRÁRIA,
CORRENTE I, E QUE SE ENCONTRA 
CONDUZINDO UMA
• NUM CAMPO MAGNÉTICO NÃO UNIFORME
O fio tem uma secção uniforme. A força magnética sobre
um segmento muito pequeno é

 
dFB  Ids  B
A força sobre o fio todo é
b

 
FB  I  ds  B
a
• NUM CAMPO MAGNÉTICO UNIFORME
b

 
FB  I  ds  B
a
'

 b  
FB  I   ds   B
a 

 

FB  I 'B
5
FORÇA MAGNÉTICA NUMA ESPIRA DE FORMA ARBITRÁRIA
NUM CAMPO MAGNÉTICO UNIFORME
 

 
FB  I  ds  B

 ds  0
 porque a soma dos vectores
um polígono fechado

ds é

FB  0
Nenhuma força magnética actua sobre a espira
6
MOMENTO (TORQUE) SOBRE UMA ESPIRA DE CORRENTE NUM CAMPO MAGNÉTICO
UNIFORME

 
FB  I  ds  B
• O CAMPO MAGNÉTICO É PARALELO AO PLANO DA ESPIRA
b
 
ds  B  dsB sin 
Lembrando que 
a
Para os lados 1 e 3 
 
 
 ds // B  ds  B  0

 FB  0
Para os lados 2 e 4 
F2  F4  IaB sin 90   IaB
Essas duas forças provocam um momento da força (torque)
em relação a O que provoca uma rotação no sentido horário.
b
2
 IaB b
 max  F2  F4
 max
b
b
b
 IaB   IaB 
2
2
2
A área da espira é
A  ab
 max  IAB
7