Unidade 6

Problema 1
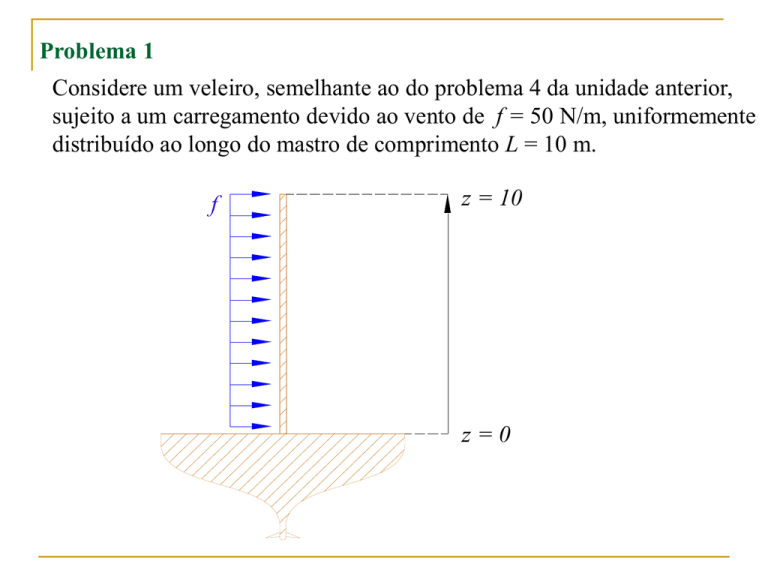
Considere um veleiro, semelhante ao do problema 4 da unidade anterior,
sujeito a um carregamento devido ao vento de f = 50 N/m, uniformemente
distribuído ao longo do mastro de comprimento L = 10 m.
f
z = 10
z=0
O carregamento causa uma deflexão no mastro, e a seguinte equação
diferencial, baseada nas leis da mecânica, pode ser usada para caracterizar
esta deflexão:
d2y
f
2

(
L

z
)
dz 2 2 EI
z
onde: E é o módulo de elasticidade da madeira
I é o momento de inércia do mastro.
Sabendo que E = 1.5 x 108 N/m2 e I = 0.06 m4, calcule a deflexão da
extremidade superior do mastro z = L, usando as seguintes condições
iniciais:
z  0  y  0

dy

 z  0  dz  0
y
Problema 2
Considere um pendulo simples como mostrado abaixo.
q
ℓ
A seguinte equação diferencial descreve seu movimento:
d 2q g
 senq  0
2
dt

Sabendo que ℓ = 30cm e g = 9.81 m/s2, calcule a velocidade que o pêndulo
assumirá quando q = 0º utilizando a seguinte condição inicial:
t  0 q 

3
Problema 3
Um reator de volume V é alimentado por uma vazão Q com uma
concentração de entrada Cin. Uma hélice faz a mistura da solução de
maneira que todo volume do reator se torne homogêneo.
Q
Cin
Q
c
A seguinte equação diferencial descreve a taxa de variação da concentração
da solução dentro do reator no tempo:
dc
V
 QC in  Qc
dt
Sabe-se que em t = 0 a concentração no reator é c0 = 10 mg/m3. Calcule
a concentração no tempo t = 10 min.
5 m3/min
Dados:
Q = 5 m3/min
Cin = 50 mg/m3
V = 100 m3
dc
V
 QC in  Qc
dt
50 mg/m3
5 m3/min
c
Problema 4
Um projétil é lançado verticalmente para o alto contra a resistência do ar.
Sabe-se que a força de resistência é proporcional ao quadrado da
velocidade. Aplicando a segunda Lei de Newton escrevemos a seguinte
equação do movimento:
dv
c 2
 g  v
dt
M
Determine o tempo necessário para que o projétil alcance sua altura
máxima sabendo que:
c
 2 m 1
M
g  10 m / s 2
v(0)  15 m / s
Problema 5
Numa reação química, uma molécula do reagente A combina-se com uma
molécula do reagente B para formar uma molécula do produto C. Sabe-se
que a concentração y(t) do produto C, no tempo, é solução do
seguinte (p.v.i.):
 dy
  k (a  y )(b  y )
 dt
 y (0)  0
Onde k é a constante de reação, a e b são, respectivamente, a concentração
inicial do reagente A e B. Considerando que:
k = 0.01
a = 70 milimoles/litro
b = 50 milimoles/litro
Determine a concentração do produto C no intervalo [0, 20].
Problema 6
Considere o conjunto massa – amortecedor dado abaixo.
M
F(t)
b
A equação diferencial que descreve o sistema é:
M
dv(t )
 bv(t )  F (t )
dt
Assuma que:
ti  ih,
v(0)  0
i  0,1,...,5
b  3Kg / s
h  0.4;
M  1Kg
F (t )  1N
a) Calcule v(2) pelo método de Euler
b) Calcule v(2) pelo método de Taylor de ordem 2
c) Sabendo que a solução exata é dada por:
e 3t t 1
v(t ) 
 
9 3 9
compare os resultados obtidos nos item a) e b) com a solução exata.
1 kg
3 kg/s
1N
dv(t )
M
 bv(t )  F (t )
dt
Problema 7
A corrente i(t) num circuito resistor – indutor (RL) de fonte alternada
pode ser expressa pela seguinte equação:
di
L  Ri  Vsen(wt )
dt
onde L é a indutância, R é a resistência e w é a freqüência da fonte.
R
L
V
i
Sabendo que V = 50 Volts, L = 1 Henry, w = 300 Hz e R = 50 Ohms,
resolva o (p.v.i.) por um método de Runge – Kutta considerando
que i(0) = 0.
50 W
1H
50 V
i
Problema 8
A carga q(t) armazenada no capacitor de um circuito resistor - indutorcapacitor (RLC) de fonte alternada pode ser expressa pela seguinte
equação:
2
d q
dq 1
L 2  R  q  Vsen( wt )
dt
dt C
onde L é a indutância, R é a resistência, C a capacitância e w é a
freqüência da fonte.
R
L
V
C
i
Sabendo que V = 50 Volts, L = 1 Henry, w = 300 Hz, R = 50 Ohms e
C = 0.25 Faraday. Resolva o (p.v.i.) por um método de Runge – Kutta
considerando que q(0) = 0 e i(0) = 0.
50 W
1H
50 V
0.25 F
i