Hipótese nula

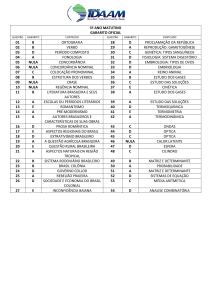
Análise Descritiva de Dados
ESTATISTICA
Aula 4
PROF: CÉLIO SOUZA
1
CURVA NORMALIDADE
• É um modelo teórico ou ideal que resulta muito
mais de uma equação matemática do que de um
real delineamento de pesquisa com posterior
coleta de dados;
UTILIDADE
• A curva normal pode ser usada na
descrição de distribuições de escores;
• Na interpretação do desvio padrão;
• Afirmações relacionadas com a noção de
probabilidade (possibilidade, predição);
A FÓRMULA
-
N
Y
e
=
1
2
(
X-X
σ
)
2
2π
onde,
Y = ordenada correspondente a um dado valor de X
π = 3,1416
e = 2,7183
Distribuição Hipotética
Simétrica
Suave
Unimodal
Forma de Sino
60
70
80
90
100
110
120
130
140
A maioria dos Q.IS situando-se entre 90 e 110 – Pouquíssimos
“gênios” > 140 e pouquíssimas criaturas menos
privilegiadas > 60;
Distribuição Assimétrica
18
Frequência
16
14
12
10
8
6
4
2
0
500
750
800
850 1000 1250 1350 1500 2000 2500
Renda (US$)
Distribuição de Renda “Per Capita” (Nações do Mundo)
Porcentagem da Área Total sob a Curva Normal Limitada
por X e por um Desvio Padrão acima de X;
9
8
7
6
5
4
3
2
1
0
1
2
3
4
5
6
7
8
9
X 10
11 + 121δ 13
14
15
16
17
18
34,17%
Porcentagem da Área Total sob a Curva Normal Limitada por X e por
Dois Desvios Padrões acima de X;
9
8
7
6
5
4
3
2
1
0
1
2
3
4
5
6
7
8
9
X
10
11
+ 121δ
13
+142δ 15 +163δ 17
34,17%
47,72%
49,87%
18
Porcentagem da Área Total sob a Curva Normal Limitada por X e por
Dois Desvios Padrões acima de X;
9
8
7
6
5
4
3
2
1
0
1
2
3
- 3δ
4
5
- 2δ
6
7
- 1δ
8
9
X
10
68,26%
95,44%
99,74%
11
+ 121δ
13
16
+142δ 15 + 3δ
17
18
Curva Normal (Escore Z)
Observando-se um no suficiente de casos, as variáveis
assumirão uma distribuição normal (Curva de Gauss)
Escore “z”
Mede o desvio em relação à média, expresso em unidades de desvio padrão;
Média
Escore
Bruto
Z=
X-X
δ
Desvio
Padrão
7.000 – 5.000
Z =
= +1.33
1.500
9
8
7
6
5
4
3
2
1
0
1
2
3
4
5
6
7
8
9
10
$5.000
11
12
13
14
15
$7.000
Z = +1.33
16
17
18
Escala Nominal
Escala Ordinal
Não-paramétricas
Não procuram estabelecer
padrões de normalidade.
Teste de Hipótese - “O resultado antecipado de um estudo ou experimento. A
solução antecipada para o problema pode ser baseada em alguma teoria, ou na
experiência e observação anteriores do pesquisador” (THOMAS & NELSON, 2002)
Escala Intervalar
Escala Racional
Possibilitam estabelecer
padrões de normalidade.
Paramétricas
Atenção: Dependendo do tipo de dados com os quais estivermos trabalhando
serão mais indicados, um ou outro tipo de análise estatística.
PROF: CÉLIO SOUZA
11








Hipótese nula (H0):
Hipótese sobre a qual o teste é montado.
Na maior parte dos casos é a hipótese de que "não
há diferença".
Em geral não é a hipótese que se deseja comprovar.
Hipótese alternativa (HA):
Hipótese que vai ser comparada à hipótese nula.
Na maior parte dos casos é a hipótese de que "há
diferença".
Em geral é a hipótese que se deseja comprovar.
PROF: CÉLIO SOUZA
12






Hipótese nula (H0):
Em geral não é a hipótese que se deseja
comprovar
"não estabelece padrão de normalidade".
.
Hipótese alternativa (HA):
"estabelece padrão de normalidade"".
PROF: CÉLIO SOUZA
13
- Se p > = 0.1, não existe evidência contra a hipótese
nula (H0), não é possível rejeitar a hipótese nula;
- Se p < 0.1, fraca evidência contra a H0;
- Se p < 0. 01, evidência altamente significativa contra
a H0, é possível rejeitar a hipótese nula;
- Se p < 0. 05, evidência significativa contra a H0,
rejeita-se a hipótese nula;
- Se p < 0. 001, evidência muito altamente
significativa contra a H0, é possível rejeitar a hipótese
nula.
PROF: CÉLIO SOUZA
14






Definir a hipótese nula (H0) e a hipótese alternativa
(H1);
Decidir qual o teste a ser usado, analisando se este é
válido para o problema;
Encontrar a probabilidade (p valor);
Avaliar a força da evidência contra H0 (quanto menor
for p-valor, maior é a força para rejeitar a hipótese nula);
Estabelecer as conclusões e interpretação dos
resultados.
O p-valor é a probabilidade que permite decidir sobre a
hipótese nula.
PROF: CÉLIO SOUZA
15
É o coeficiente numérico que indica a extensão na
qual duas variáveis se relacionam ou associam.
 A técnica utilizada para calcular a correlação é o Coeficiente de
Correlação do Momento Produto de Person (r).

Valor
Significado
0
Inexistente
0 < r < 0,2
Baixa
0,2  r < 0,4
Média baixa
0,4  r < 0,6
Média
0,6  r < 0,8
Média alta
0,8  r < 1,0
Alta
1,0
Perfeita
Fonte: Sigmound, 1964
SIGMOUND, R. Estatística não-paramétrica. SP.McGraw-Hill, 1964.
PROF: CÉLIO SOUZA
16




Escore “z” na variável X
Escore “z” na variável X
Número de casos




Somatório dos escores de X e Y
Médias
Desvios padrão

PROF: CÉLIO SOUZA
17
PROF: CÉLIO SOUZA
18
 Qualquer
dúvida, pergunte.
PROF: CÉLIO SOUZA
19