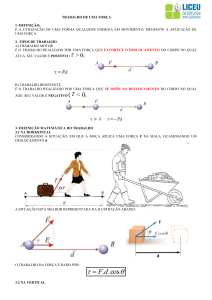
Energia cinética e trabalho
Energia
As leis de Newton permitem analisar vários movimentos. Essa análise
pode ser bastante complexa, necessitando de detalhes do movimento
simplesmente inacessíveis. Exemplo: qual é a velocidade final de um
carrinho na chegada de um percurso demontanha russa? Despreze a
resistência do ar e o atrito, mas resolva o problema usando as leis de
Newton.
v 0
v ?
Energia II
Aos poucos cientistas e engenheiros desenvolveram uma técnica
muitas vezes mais poderosa para analisar o movimento. Essa maneira
acabou sendo estendida a outras situações , tais como:
reações químicas, processos geológicos e funções biológicas.
Essa técnica alternativa envolve o conceito de energia, que aparece em
várias formas e tipos.
Definição de energia: grandeza escalar associada a um estado de um
ou mais corpos.
Essa definição é muito vaga e para chegar a algum lugar vamos
nos concentrar inicialmente em uma forma apenas de energia.
Energia III
Importância do conceito de energia:
• Processos geológicos
• Balanço energético no planeta Terra
• Reações químicas
• Balanço energético no corpo humano
Energia cinética e trabalho
Relação entre forças agindo sobre um corpo e a energia cinética:
1) A abordagem a partir do conceito de energia representa um
bom atalho para resolução de problemas,
2) A idéia de energia revela-se de fato fundamental na Física.
Problema 1 D: corpo sob ação de uma força resultante constante:
F
a
m
v v
2
2
0
F
2ax 2
x
m
1 2 1
2
F
x
mv
mv
0
2
2
Se um objeto está sujeito a uma força resultante constante está é a variação
de velocidade após um percurso Δx
Trabalho
O trabalho das forças resultantes é dado por:
Wres Fx
Unidades SI:
1 2 1
2
F
x
mv
mv
0
2
2
1 joule = 1 J = 1 N.m = 1 kg.m2.s-2
Atenção: para ter trabalho é necessário ocorrer um deslocamento!
Trabalho II:
para ter trabalho é necessário ocorrer
um deslocamento!
Trabalho realizado pelo guindaste
ao erguer a escultura:
m 2000kg
y 1,5m
W 2000 g 1,5 3,0 10 J
4
Para manter a escultura erguida o
guindaste não realiza trabalho
Trabalho em 2 ou 3 dimensões
(exemplo para uma força constante)
Trabalho devido a uma força F
em 1 dimensão:
W Fx
Trabalho devido a uma força F
em mais de uma dimensão:
W F r Fr cos
F
r
Energia cinética II
A quantidade
mv 2 , cuja variação é expressada em um
2
slide anterior em relação ao que definimos como trabalho
é a energia cinética:
1
2
K mv
2
Lembrando as unidades:
1 joule = 1 J = 1 kg.m2.s-2
A energia cinética não pode assumir valores negativos e é uma
grandeza escalar.
O trabalho também é uma grandeza escalar e pode assumir valores
negativos…
Teorema trabalho - energia cinética
Exemplo para o trabalho da força peso F = -mg
K K f K i Wres Fy
y 0
F 0
W 0
K 0
F mg
y 0
F 0
W 0
K 0
Trabalho de uma força constante
Força peso: cálculo do trabalho de uma força constante em 1 dimensão
m 10,2kg
W mgy mg( y f y i )
ou
yf
m g dy mg( y
f
yi )
yi
W 100J
Trabalho para uma força variável
Em 1 dimensão:
F F ( x)
O trabalho é a área da curva da força!
W F(x i )x i
x2
x1
Trabalho para uma força variável
Em 1 dimensão:
F F ( x)
O trabalho é a área da curva da força!
W F(x i )x i
x2
x1
No limite
x 0
x2
W F( x )dx
x1
Trabalho para uma força variável
F
F F ( x)
Em 1 dimensão:
W
X
Demonstração do teorema trabalho – energia cinética
xf
xf
vf
dv
W F ( x )dx m dx m vdv
dt
xi
xi
vi
1
m v 2f v i2 K
2
Trabalho para uma força variável
Em 1 dimensão:
F F ( x)
Teorema trabalho – energia cinética
xf
1
1
2
2
W F(x)dx mvf mvi K
2
2
x
i
ou
W K
O trabalho de uma força é igual a variação de sua energia cinética
ainda um exemplo de trabalho de forças constantes
Modelo para resolver o problema:
F
N
fa
mg
Δx
Trabalho realizado pelos carregadores:
Wc Fx
Trabalho realizado pela força de atrito:
Watr f atr x c mg x
…continuação do mesmo exemplo:
Se o carrinho se desloca com velocidade constante:
K 0
Consistente com o fato de que o trabalho total ser nulo:
Wc Watr 0
A força resultante é nula:
F F f
a
0
Forças que variam com a posição:
Exemplo a ser estudado: trabalho da força elástica:
F kx
Força para esticar uma mola
Força restauradora da mola
Fs
Trabalho realizado pela força da mola
F
xf
Wmola
xi
F ( x )dx
xi
xf
x
xf
k xdx
xi
1
k ( x 2f x i2 )
2
Se xi < xf
W<0
O trabalho sobre a mola pelo agente externo
é o valor obtido acima com sinal trocado
Forças que variam tanto de módulo quanto de direção
Trabalho dWf de uma força F agindo
ao longo de um deslocamento infinitesimal
Ausência de trabalho no movimento circular
uniforme
ds
Fc
v
dW Fc ds 0
Pelo teorema trabalho – energia cinética:
v cte
K 0 W
Potência
Trabalho realizado pelo atleta sobre o
halteres:
Trabalho realizado pelo atleta:
F
y
r
F 150 N
r 20m
W 3000J
m 75kg
y 2m
m 75kg
W Fy 3000 J
Potência II
Até agora não nos perguntamos sobre quão rápido é realizado um trabalho!
Potência, P, é a razão (taxa) de realização do trabalho por unidade de tempo:
dW
P
dt
Unidades SI:
J/s
W
Considerando o trabalho em mais de uma dimenão:
dr
dW
P
F
dt
dt
O segundo termo é a velocidade:
W F r
P F v
100 m rasos versus maratona:
trabalho
massa do atleta = 70 kg
Trabalho mecânico realizado pelo atleta:
Maratona : 140 J.m-1
Corrida de 100 m : 210 J.m-1
Trabalho realizado pelo corredor de 100 m rasos: 2,1x104 J
Trabalho realizado pelo maratonista: 5,9 x106J
Esses dados foram obtidos de:
P. A. Willems et al., The Journal of Experimental Biology 198, 379 (1995)
100 m rasos versus maratona:
potência
Trabalho realizado pelo corredor de 100 m rasos = 2,1x104 J
Trabalho realizado pelo maratonista =5,9x106J
Potência do corredor de 100 m rasos:
2,1 104 J
P100
2100W
10 s
Potência do corredor de maratona:
Pmar
5,9 106 J
816W
2 60 60 s
Um pouco de história
definição da unidade
cavalo-vapor:
1 cv =746 W
Esquema da 1a máquina
a vapor de J. Watt - 1788
James Watt 1736 - 1819
Unidade de potência criada por Watt para fazer
o marketing de sua máquina em uma sociedade
fortemente depedente do (e acostuamada ao)
trabalho realizado por cavalos.
1a motivação: retirada da água das minas de carvão.