revisão matemática

REVISÃO MATEMÁTICA
Unidades de medidas:
Medidas de comprimento
Medidas Angulares
Medidas de comprimento
A origem do metro ocorreu em 1791 quando a Academia de Ciências de
Paris o definiu como unidade padrão de comprimento. Sua dimensão era representada
por 1/10.000.000 de um arco de meridiano da Terra.
Em 1983, a Conferência Geral de Pesos e Medidas estabeleceu a definição
atual do “metro” como a distância percorrida pela luz no vácuo durante o intervalo de
tempo de 1/299.792.458 s(Veiga et al, 2007, p. 15)
Medida Angular
Radiano: Um radiano é o ângulo central que subentende um arco de circunferência
de comprimento igual ao raio da mesma. É uma unidade suplementar do SI para
ângulos planos.
2πR — 360º
arco = R = raio
Unidade Sexagesimal:
Grau
°
1° = (∏/180) rad
Minuto ‘
1’ = 1°/60 = (∏/10800) rad
Segundo “
1” = 1°/3600 = (∏/648000) rad
Unidade Decimal:
Grado
1 Grado = 1/400 da circunferencia
Exemplos e Exercícios
1) Transformação de ângulos:
Transforme os seguintes ângulos em graus, minutos e segundos para graus e frações
decimais de grau.
a) 32º 28’ 59” = 32, 48305556º
b) 17º 34’ 18,3” = 17,57175º
c) 125º 59’ 57” = 125,9991667º
2) Soma e subtração de ângulos:
30°20’ + 20° 52’ = 51º12’
28°41’ + 39°39’ = 68°20’
42°30’ – 20°40’ = 21°50’
FAÇA AS MESMAS CONTAS UTILIZANDO SUA CALCULADORA
Cuidados ao utilizar calculadora
Ao aplicar-se a função sem a transformação do ângulo pode-se incorrer em erros
nos cálculos futuros, como é possível observar no exemplo a seguir:
Para o ângulo citado: α = 22º 09’ 04”
Calculando-se o valor da função seno sem converter o valor do ângulo, obtém-se:
sen 22,0904 = 0,376069016
Já transformando-o para graus decimais obtém-se:
sen 22,1511111º = 0,377050629
Considerando uma distância de 300m, entre um vértice de uma poligonal e um
ponto de detalhe qualquer, pode-se observar a seguinte diferença no valor de Δx
calculado.
Δx = 300 . sen 22,0904 = 300 . 0,376069016 → Δx = 112,821m
Δx = 300 . sen 22,15111110 = 300 . 0,377050629 → Δx = 113,115m
Uma diferença de 29,4 cm
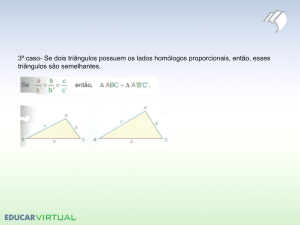
Trigonometria Plana
A soma dos ângulos internos de um triângulo é igual a 180°. A partir da figura
podem ser estabelecidas as seguintes relações:
A partir da figura ao lado, determine
os valores de Seno, Cosseno e
Tangente dos angulos α e β
Relações métricas (Triang. Retangulo)
Para um triângulo retângulo ABC pode-se estabelecer algumas relações entre as
medidas de seus elementos:
Onde:
b, c: catetos;
h: altura relativa à hipotenusa;
a: hipotenusa;
m, n: projeções ortogonais dos catetos sobre a hipotenusa.
As seguintes relações métricas podem ser definidas:
a) O quadrado de um cateto é igual ao produto da hipotenusa pela projeção desse
cateto sobre a hipotenusa.
b² = a . n
c² = a . m
b) O produto dos catetos é igual ao produto da hipotenusa pela altura relativa à
hipotenusa.
b.c = a.h
c) O quadrado da altura é igual ao produto das projeções dos catetos sobre a
hipotenusa.
h² = m . n
d) O quadrado da hipotenusa é igual a soma dos quadrados dos catetos.
a² = b² + c²
(Teorema de Pitágoras)
Relações métricas (Triang. Qualquer)
LEI DOS SENOS
“Num triângulo qualquer a razão entre cada lado e o seno do ângulo oposto é
constante e igual ao diâmetro da circunferência circunscrita”.
LEI DOS COSSENOS
“Num triângulo qualquer, o quadrado da medida de um lado é igual à soma dos
quadrados das medidas dos outros dois, menos o dobro do produto das
medidas dos dois lados pelo cosseno do ângulo que eles formam”.
A² = b² + c² – 2.b.c. cos A
A fim de medir a largura de um rio em um certo local, adotou-se o seguinte
procedimento: Marcou-se um ponto B em uma margem; 30 m à direita marcou-se um
ponto C, de tal forma que AB e BC sejam perpendiculares, do ponto C mediu-se um
ângulo de 30°, dessa forma conclui-se que a largura do rio (AB) é:
A
B
30 m
C
Exercícios
1) Um observador na margem de um rio vê o topo de uma torre na outra margem
segundo um ângulo de 56° 00’00”. Afastando-se de 20,00 m, o mesmo observador vê a
mesma torre segundo um ângulo de 35° 00’00”. Calcule a largura do rio (CEFET, 1984).
Exercício (Continuação)
2) Para determinar a largura de um rio, um topógrafo mediu, a partir de uma base de
20,00m de comprimento os ângulos A e B, conforme figura. Calcule valor de h.