Circunferência e Círculo I

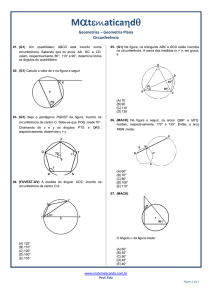
Circunferência
 Se O é um ponto do plano e r um número real positivo, chama-se
circunferência de centro O e raio r o lugar geométrico dos pontos do
plano que estão à distância r do ponto O.
A
B
P
r
r
r
r
O
r
r
E
D
C
Elementos
P
A
O
r
r
O
Q
Corda PQ
Diâmetro AB
C= 2r
D = 2r
B
Elementos
B
Arco AMB
N
M
A
Arco ANB
Arcos e ângulos
A≡B
arco completo
A≡B
arco nulo
Arcos e ângulos
B
O
Arco de meia volta
(Semicircunferência)
A
Círculo
 O conjunto constituído por uma circunferência e pelos
pontos interiores a ela é chamado círculo ou disco.
O
r
Posições relativas de ponto e circunferências
P
O
r
B
A
 O ponto A é interno à circunferência
dOA < r
 O ponto B pertence à circunferência
dOB = r
 O ponto P é exterior à circunferência
dOP > r
Posições relativas de reta e circunferências
r é tangente à circunferência
dOP = r
r
r
P
⇔
O
r e a circunferência têm um único
ponto comum.
Posições relativas de reta e circunferências
A
P
B
s é secante à circunferência
dOP < r
O
⇔
s
s e a circunferência têm dois
pontos comuns.
Posições relativas de reta e circunferências
t é exterior à circunferência
dOP > r
⇔
O
P
t
t e a circunferência não têm
ponto comum.
Propriedades da reta tangente à circunferência
 Uma reta é tangente a uma circunferência
se, e somente se, ela é perpendicular ao
raio no ponto de tangência.
r
O
r
P
 Por um ponto de uma circunferência, podese traçar uma única tangente a essa
circunferência.
Propriedade da reta secante à circunferência
 Uma reta secante que passa pelo centro da
circunferência é perpendicular a uma corda
se, e somente se, divide essa corda ao meio.
s
B
O
M
A
s ⊥ AB por O ⇔ AM = MB
Conseqüência
 Um diâmetro perpendicular a uma corda
divide essa corda ao meio.
C
B
O
M
D
A
CD ⊥ AB por O ⇔ AM = MB
Posições relativas de duas circunferências
C2
C1
A
R
r
B
C1 é externa C2
Todos os pontos de C1 são
externos a C2
⇔
dAB > r + R
Posições relativas de duas circunferências
C2
C1
B
A
R
r
P
C1 e C2 são tangentes externamente em P
C1 e C2 têm um só ponto comum
e não têm ponto interior comum
⇔
dAB = r + R
Posições relativas de duas circunferências
C2
C1
B
A
r
R
C1 e C2 são secantes
Têm dois pontos comuns
⇔
R – r < dAB < R + r
Posições relativas de duas circunferências
C1
P
A
C2
B
C1 e C2 são tangentes
internamente em P
Têm um só ponto comum e os
dAB = R – r
demais pontos de C1 são
⇔
interiores a C2
Posições relativas de duas circunferências
C2
C1
A
B
C1 é interna a C2
Todos os pontos de C1 são
interiores a C2
⇔
0 ≤ dAB < R – r
Ângulo central

Chama-se de ângulo central de uma circunferência todo ângulo
que tem como vértice o seu centro.
B
C
 O 

D
A
E
F
A cada ângulo central corresponde
um arco, interseção do ângulo com
a circunferência.
Ângulo central

Um ângulo central tem a mesma medida do arco correspondente.
A
O
AÔB é ângulo central

m(AÔB) = m(AB) = 
B
Unidade de ângulo e arco
Representação
Medida em
graus
Arco
completo
360º
Arco de
meia
volta
180º
Arco de
¼ de
volta
90º
Arco nulo
0º
Ângulo Inscrito

Chama-se ângulo em uma circunferência todo ângulo cujo
vértice é um de seus pontos e cujos lados são secantes a ele.
A
APB é ângulo inscrito
O

P
B
m(APB) =  =
AB
2
Ângulo Inscrito - Propriedade

Ângulos inscritos em um mesmo arco são congruentes.
Q
P
R
Os ângulos inscritos de vértices
P, Q e R são congruentes
B
A
m(APB) = m(AQB) = m(ARB) =
AB
2
Ângulo Inscrito - Propriedade

Todo ângulo inscrito numa semicircunferência é reto.
M
N
A
B
P
AB diâmetro da circunferência, os
ângulos de vértices M, N e P são
retos, porque o arco AB mede 180o.
Ângulo Inscrito - Propriedade

Todo triangulo inscrito numa semicircunferência e retângulo.
M
r
A
r
r
B
Como conseqüência a mediana
relativa a hipotenusa tem medida
igual a metade da hipotenusa.