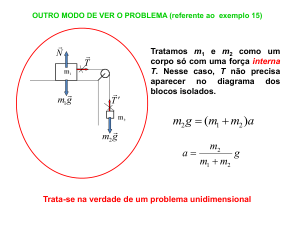
Exemplo 15. Calcular a tensão nos fios e a aceleração dos blocos. Não há atrito entre o
bloco e a superfície. Os fios e a roldana são ideais.
N
T
N m g
1
Bloco 1
x
y
T
m1 g
F 0 N m g
F ma T m a
y
1
x
F
Bloco 2
y
x
m ay
m2 g T m2 a
m2 g
T m2 g m2 a
Como
T T , igualamos (1) e (2)
m1a m2 a m2 g
a
m2
g
m1 m2
1
(2)
m1a m2 g m2 a
(m1 m2 )a m2 g
T m1 a
m1 m2
g
m1 m2
(1)
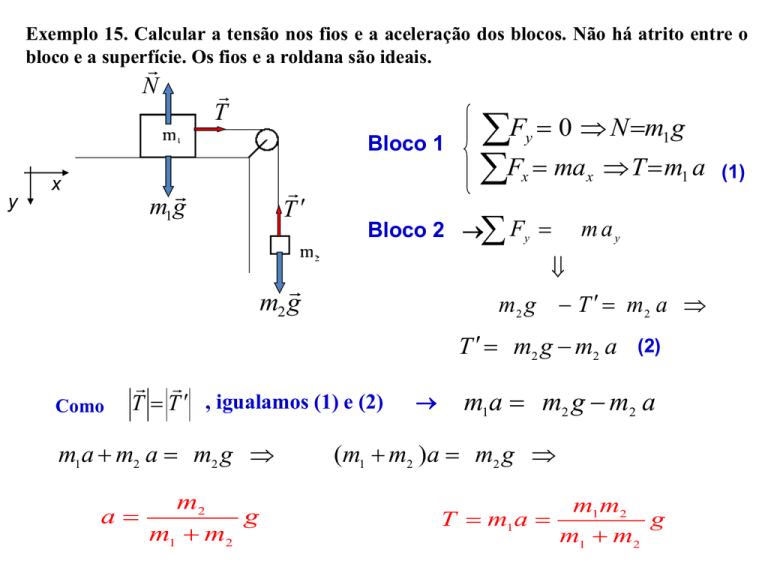
OUTRO MODO DE VER O PROBLEMA
N
m1 g
T
T
Tratamos m1 e m2 como um
corpo só com uma força interna
T. Nesse caso, T não precisa
aparecer no diagrama dos
blocos isolados.
m2 g (m1 m2 )a
m2 g
m2
a
g
m1 m2
Trata-se na verdade de um problema unidimensional !
A TERCEIRA LEI DE NEWTON
A TERCEIRA LEI DE NEWTON transmite a noção de que as forças são sempre
interacções entre dois corpos:
F12
“Se dois corpos interagem, a força
exercida pelo
corpo 1 sobre o corpo 2 é
igual em módulo , mas oposta em direcção à força F21 exercida pelo corpo 2 sobre
o corpo 1”:
Exemplo
F12 F21
As forças F e F21
12
F12
constituem um
par acção-reacção
As forças do par ação-reação:
têm mesmo módulo e mesma direcção, e
sentidos opostos
nunca actuam no mesmo corpo
nunca se cancelam
F21
1. O boxeador pode golpear um saco massivo com uma força considerável.
2. Com o mesmo golpe ele pode exercer apenas uma pequenina força sobre um lenço
de papel no ar.
(1)
Figura 1. O punho golpeia o saco (e
produz uma cavidade no saco) enquanto
o saco golpeia o punho de volta (e
interrompe o movimento do punho). Ao
atingir o saco, há uma interacção com o
saco que envolve um par de forças. O
par de forças pode ser muito grande.
(2)
Figura 2. O punho do boxeador pode
apenas exercer tanta força sobre o lenço
de papel quanto o lenço é capaz de
exercer sobre o punho.
Outros exemplos da 3ª Lei de Newton
PRINCÍPIO DA CONSERVAÇÃO DA QUANTIDADE DE MOVIMENTO
(OU LEI DA CONSERVAÇÃO DO MOMENTO LINEAR)
Na ausência de forças externas, a quantidade de movimento permanece constante
(o momento total de um sistema isolado permanece constante)
Supomos duas partículas que interagem entre si.
De acordo com a terceira lei de Newton
p1 m1v1
e
F21
F12
formam um par acção e reacção e
F12 F21
Podemos expressar essa condição como
m1
F12 F21 0
dp1 dp 2 d ( p1 p2 )
0
dt
dt
dt
F12
F21
p2 m2v2
m2
p1 p2 ptotal constante
(num instante t)
Exemplo 16. Suponha que um peixe nada em direcção a outro peixe menor. Se o
peixe maior tem uma massa de 5 kg e nada com velocidade de 1 m/s na direcção de
um peixe de 1 kg que está parado (v=0), qual será a velocidade do peixe grande logo
após o almoço? Desprezamos o efeito da resistência da água.
O momento linear total antes do almoço = O momento linear total depois do almoço
pantesdo almoço pdepoisdo almoço constante
MV mv MV 'mv ' constante
(5 kg)(1 m/s) (1 kg)(0) (5 kg 1 kg)V '
5 kg m/s (6 kg)V '
5 kg m/s (6 kg)V '
V ' (5 / 6) m/s
V ' 0.8 m/s
FORÇA GRAVITACIONAL
A força gravitacional é a força mútua de atracção entre dois corpos quaisquer do
Universo
A lei da gravitação de Newton afirma que toda a partícula do Universo atrai qualquer
outra partícula com uma força que é directamente proporcional ao produto das
massas das partículas e inversamente proporcional ao inverso do quadrado da
distância entre elas.
m1m2
Fg G 2 u
r
onde G é a constante gravitacional universal
No SI G 6.67 1011 Nm2 / kg 2
A MASSA INERCIAL que aparece na segunda lei de Newton ( f ma ) e que tem a
ver com a resistência ao movimento e a MASSA GRAVITACIONAL que aparece na lei
da gravitação universal são as mesmas.
A força gravitacional entre duas partículas é
atractiva
F12 F21
F12
F21
ACELERAÇÃO DA GRAVIDADE
Podemos reescrever a lei da gravitação Universal de
Newton usando a segunda lei de Newton
Fg mgu
Fg
onde g é a aceleração da gravidade
Comparando com a expressão da lei da
gravitação de Newton
mM T
mgu G 2 u
r
obtemos
MT
g G 2
r
O peso de um corpo na Terra é a força com
que a Terra atrai a massa com que esse
corpo é feito .
Foi Newton que esclareceu a
diferença entre a MASSA e o PESO
de um corpo
EXEMPLOS DE FORÇA GRAVITACIONAL
r
CENTRO DE MASSA
dv d dx d 2 x
a
2
dt dt dt dt
A aceleração instantânea de uma partícula é
SISTEMA DE 2 PARTÍCULAS
F1
F12
F21
F2
Para o sistema de duas partículas, temos
F1 F2 F
onde
F é a força externa resultante que actua sobre o sistema
m1a1 m2 a2 F
d 2 m1 x1 m2 x2
F
2
dt
d 2 x1
d 2 x2
m1 2 m2 2 F
dt
dt
(1)
CENTRO DE MASSA (cont)
Definimos
xCM
m1 x1 m2 x2
m1 m2
Substituindo na equação (1)
portanto
m1 x1 m2 x2 (m1 m2 ) xCM
d 2 m1 x1 m2 x2
F
2
dt
(1)
obtemos
d 2 xCM
F (m1 m2 )
(m1 m2 )aCM
2
dt
d 2 xCM
ou F M
MaCM
2
dt
onde M=m1+m2 é a massa total do sistema
O sistema se comporta como se toda massa estivesse concentrada no ponto xCM
(centro de massa) e a força externa agisse sobre ele.
xCM
M
F
d 2 xCM
F M
dt 2
Exemplo 17. Calcular o centro de massa dos seguintes sistemas de duas partículas.
xCM
m1 x1 m2 x2
m1 m2
x1
(a)
x2
xCM
xCM
mx1 mx2
2m
xCM
x1 x2
2
(b)
x1
x2
xCM
muito pequeno
xCM
m1 x1 m2 x2 m1 x1
m1 m2
m1
m1 m2
x
xCM x1
muito pequeno
x
m1 m2
EXEMPLO
Centro de massa
No caso particular em que
dxCM
vCM cte.
dt
F 0
d 2x
a 2 0
dt
m = 80 kg
m = 60 kg
Exemplo 18. Dois patinadores no gelo (sem atrito
com o chão) encontram-se inicialmente a uma
distância de 12 m. Eles puxam as extremidades de
uma corda até se encontrarem. Em que ponto eles
se encontram? O resultado depende das forças
exercidas por eles?
Só há forças internas ao sistema o centro de massa tem velocidade constante.
xCM
m1 x1 m2 x2
m1 m2
xCM
0 80 kg 12 m 60 kg
m 5.1 m
80 60
Os patinadores se encontrarão a 5.1 m da posição inicial do patinador da esquerda.
O resultado não depende das forças exercidas por eles uma vez que são forças internas
CENTRO DE MASSA PARA N PARTÍCULAS NUMA DIMENSÃO
xCM
m1 x1 m2 x2 mN xN
1
m1 m2 mN
M
N
m x
i 1
i i
CENTRO DE MASSA PARA N PARTÍCULAS EM TRÊS DIMENSÕES
ou
1
rCM
M
mi ri
N
i 1
CENTRO DE MASSA PARA CORPOS CONTÍNUOS E UNIFORMES
Se um corpo consiste de uma distribuição contínua de massa, podemos dividi-lo em
porções infinitesimais de massa dm e a soma transforma-se numa integral:
onde
A posição do centro de massa de um sistema pode ser determinada como a
posição média da massa do sistema