Chapter 2

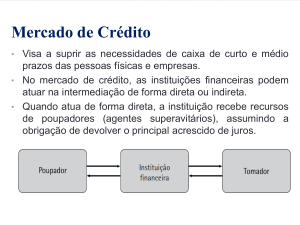
Sistemas Numéricos e Códigos
Capítulo 2
Prof. Gustavo Fernandes de Lima
<[email protected]>
Os temas abordados nesse capítulo são:

Conversão entre sistemas numéricos.



Representação de números decimais com o código BCD.



Decimal, binário, hexadecimal.
Contagem hexadecimal.
Prós e contras do uso do BCD.
Diferenciação entre o BCD e o binário puro.
Finalidade dos códigos alfanuméricos (ex., o código ASCII).
slide 2
© 2011 Pearson Prentice Hall. Todos os direitos reservados.
2.1 Conversões de Binário para Decimal

Converter binário em decimal através da soma das posições
que contêm um 1:

Exemplo com um maior número de bits:
slide 3
© 2011 Pearson Prentice Hall. Todos os direitos reservados.
2.1 Conversões de Binário para Decimal

Com o método double-dabble evita-se a adição de números
grandes e o acompanhamento dos pesos das colunas,
através do seguinte procedimento:
1.
2.
3.
4.
slide 4
Anote o 1 da extrema esquerda no número binário.
Dobre-o e acrescente o bit seguinte da direita.
Anote o resultado sob o próximo bit.
Continue com as etapas 2 e 3 até terminar o número binário.
© 2011 Pearson Prentice Hall. Todos os direitos reservados.
2.1 Conversões de Binário para Decimal

slide 5
Os números binários verificam o método double-dabble.
© 2011 Pearson Prentice Hall. Todos os direitos reservados.
2.1 Conversões de Binário para Decimal
Questões para revisão
 Converta o binário 1000110110112 em seu equivalente
decimal somando os produtos dos dígitos e pesos.
2.048+0+0+0+128+64+0+16+8+0+2+1=2.26710
 Qual é o peso do MSB de um número de 16 bits?
215 = 32.768
 Repita a conversão na questão 1 usando o método doubledabble.
12 4 8 17 35 70 141  283 566 1.133
2.26710
slide 6
© 2011 Pearson Prentice Hall. Todos os direitos reservados.
2.2 Conversões de Decimal para Binário

Trata-se de um processo inverso ao descrito em 2.1.
Todas as posições devem ser contabilizadas.

Outro exemplo:
slide 7
© 2011 Pearson Prentice Hall. Todos os direitos reservados.
2.2 Conversões de Decimal para Binário

Divisão repetida

Divida o número decimal por 2. Escreva o restante após cada
divisão até obter o quociente 0. O primeiro restante é o LSB. O
último é o MSB.
slide 8
© 2011 Pearson Prentice Hall. Todos os direitos reservados.
2.2 Conversões de Decimal para Binário
slide 9
© 2011 Pearson Prentice Hall. Todos os direitos reservados.
2.2 Conversões de Decimal para Binário

Converta 3710 em binário:
slide 10
© 2011 Pearson Prentice Hall. Todos os direitos reservados.
2.2 Conversões de Decimal para Binário
Questões de revisão
 Converta 8310 em binário usando os dois métodos
apresentados.
8310 = 64 + 0 + 16 + 0 + 0 + 2 + 1 = 10100112
 Converta 72910 em binário usando os dois métodos
apresentados. Verifique sua resposta, fazendo a conversão
de volta para decimal.
72910 = 512+0+128+64+0+16+8+0+0+1=10110110012
 Quantos bits são necessários para contar até 1 milhão em
decimal?
219 = 524.288 e 220 = 1.048.576
slide 11
© 2011 Pearson Prentice Hall. Todos os direitos reservados.
2.3 Sistema de Numeração Hexadecimal

O hexadecimal permite a manipulação de longas cadeias
binárias, utilizando grupos de 4 bits - base 16.
Possui dezesseis símbolos possíveis: 0-9 e A-F.
slide 12
© 2011 Pearson Prentice Hall. Todos os direitos reservados.
2.3 Sistema de Numeração Hexadecimal

Relações entre os números
binários.
slide 13
hexadecimais, decimais e
© 2011 Pearson Prentice Hall. Todos os direitos reservados.
2.3 Sistema de Numeração Hexadecimal
Conversão de hexa em decimal

A conversão de hexa para decimal é feita através da
multiplicação de cada dígito hexadecimal por seu peso
posicional.

Em um segundo exemplo, o valor 10 é substituído por A e o
15 é substituído por F.
slide 14
© 2011 Pearson Prentice Hall. Todos os direitos reservados.
2.3 Sistema de Numeração Hexadecimal
Conversão de decimal em hexadecimal

A conversão de decimal para hexadecimal, utilizando-se o
método de divisão repetida (idem 2.2), ocorre através da
divisão do número decimal por 16.

O primeiro restante é o LSB. O último é o MSB.
slide 15
© 2011 Pearson Prentice Hall. Todos os direitos reservados.
2.3 Sistema de Numeração Hexadecimal
Conversão de decimal em hexadecimal

Converta 42310 para hexadecimal:
slide 16
© 2011 Pearson Prentice Hall. Todos os direitos reservados.
2.3 Sistema de Numeração Hexadecimal
Conversão de decimal em hexadecimal

Converta 21410 para hexadecimal:
slide 17
© 2011 Pearson Prentice Hall. Todos os direitos reservados.
2.3 Sistema de Numeração Hexadecimal
Conversão de hexa em binário

Cada dígito hexa é convertido no equivalente bináiro de 4
bits (Tabela 2.1).

Os zeros à esquerda podem ser adicionados à esquerda do
MSB para preencher o último grupo.
slide 18
© 2011 Pearson Prentice Hall. Todos os direitos reservados.
2.3 Sistema de Numeração Hexadecimal
Conversão de binário em hexa

Para converter binário para hexadecimal, deve-se agrupar
os bits em quatro, começando-se com o LSB. Cada grupo é,
então, convertido no hexadecimal equivalente.

Os zeros à esquerda podem ser adicionados à esquerda do
MSB para preencher o último grupo.
slide 19
© 2011 Pearson Prentice Hall. Todos os direitos reservados.
2.3 Sistema de Numeração Hexadecimal
Questões para revisão
 Converta 24CE16 em decimal.
24CE16 = 2 x 163+4 x 162+C x 161+E x 160 = 9.42210
 Converta 311710 em hexa e, em seguida, em binário.
311710 = C2D16 = 1100 0010 11012 = 1100001011012
 Converta 10010111101101012 em hexa.
1001 0111 1011 01012 = 97B516
slide 20
© 2011 Pearson Prentice Hall. Todos os direitos reservados.
2.4 Código BCD
BCD (binary-coded-decimal) é uma maneira muito utilizada
de apresentar números decimais em formato binário.
 Combina características dos sistemas decimal e binário.
 Cada dígito é convertido em um binário equivalente.
 BCD não é um sistema numérico. É um número decimal
com cada dígito codificado para seu equivalente binário.
 Um número BCD não é o mesmo que um número binário
direto.
 A principal vantagem do BCD é a relativa facilidade de
conversão em decimal e vice-versa.

slide 21
© 2011 Pearson Prentice Hall. Todos os direitos reservados.
2.4 Código BCD



Converta o número 87410 para BCD.
Cada dígito decimal é representado por 4 bits.
Cada grupo de 4 bits não pode ser superior a 9.
Outro exemplo:
slide 22
© 2011 Pearson Prentice Hall. Todos os direitos reservados.
2.4 Código BCD

Converta 0110100000111001 (BCD) em seu equivalente
decimal.
slide 23
© 2011 Pearson Prentice Hall. Todos os direitos reservados.
2.4 Código BCD
Comparação entre BCD e binário puro
Exemplo:
13710 = 100010012 (binário)
13710 = 0001 0011 0111 (BCD)
slide 24
© 2011 Pearson Prentice Hall. Todos os direitos reservados.
2.4 Código BCD
Questões para revisão
 Represente o valor decimal 178 no seu equivalente binário
puro. Em seguida, codifique o mesmo nº em BCD.
101100102 e 0001 0111 1000 (BCD)
 Quantos bits são necessários para representar, em BCD, um
nº decimal de oito dígitos?
32
 Qual a vantagem da codificação em BCD de um nº decimal
quando comparada com o binário puro? E qual é a
desvantagem?
Conversão mais fácil/código BCD requer mais bits.
slide 25
© 2011 Pearson Prentice Hall. Todos os direitos reservados.
2.6 Relações entre as Representações
Numéricas

Números decimais 1 – 15 em binário, hexa, BCD e Gray.
slide 26
© 2011 Pearson Prentice Hall. Todos os direitos reservados.
2.8 Códigos Alfanuméricos



O código alfanumérico representa todos os caracteres e as
funções encontrados em um teclado de computador: 26
letras minúsculas e 26 maiúsculas, 10 dígitos, 7 sinais de
pontuação, de 20 a 40 outros caracteres.
O código alfanumérico mais utilizado é o ASCII - American
Standard Code for Information Interchange (Código Padrão
Americano para Intercâmbio de Informações).
Trata-se de um código de 7 bits: 27 = 128 possíveis grupos
de código. Pode ser utilizado para transferir informações
entre computadores, entre computadores e impressoras
e para armazenamento interno.
slide 27
© 2011 Pearson Prentice Hall. Todos os direitos reservados.
2.8 Códigos Alfanuméricos
ASCII - American Standard Code for Information Interchange
(Código Padrão Americano para Intercâmbio de Informações)
slide 28
© 2011 Pearson Prentice Hall. Todos os direitos reservados.
Bibliografia

TOCCI, Ronald J.; WIDMER, Neal S.; MOSS, Gregory L..
Sistemas digitais: princípios e aplicações. 11. ed. São
Paulo : Pearson Prentice Hall, 2011.
slide 29
© 2011 Pearson Prentice Hall. Todos os direitos reservados.
Fim
OBRIGADO
<[email protected]>
slide 30
© 2011 Pearson Prentice Hall. Todos os direitos reservados.