Material de apoio: cinemática

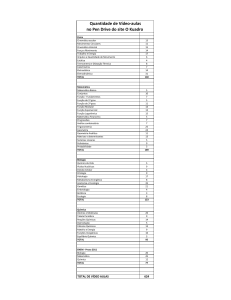
Material de apoio: cinemática
z (t )
S

r (t )

ux
x (t )

uz
P

uy
y (t )
O




r ( t )  x ( t ) u x  y ( t )u y  z ( t ) u z
Vector posição do ponto P
x (t )
y (t )
z (t )
Componentes do vector posição
Coordenadas do ponto P
Dimensões : L
Unidades SI : m
Material de apoio: cinemática

vector velocidade


dr (t )
v (t ) 
dt



 v x (t )u x  v y (t )u y  v z (t )u z


v (t )  v(t )uT (t )

norma de v (t )
v(t )  v2x (t )  v2y (t )  v2z (t )
dx

v x (t )  dt (t )

dy

(t )
v y (t ) 
dt

dz

v z (t )  dt (t )

versor tangente à trajectória:
• norma unitária
•direcção da tangente à trajectória
•sentido do movimento
Dimensões : LT-1
Unidades SI : m s-1
Material de apoio: cinemática
Movimento
curvilíneo geral

ur

u

dr ur
d

r'
O

dr (t )

rd u



dr  dr ur  rd u




dr
dr
d
v (t ) 
(t ) 
(t ) ur (t )  r (t )
(t ) u (t )
dt
dt
dt




vr (t )
v (t )
Material de apoio: cinemática

uT (t1 )

r (t1 ) 
r (t2 )
O

uT (t )

uN (t )
versor tangente à trajectória

r

r (t3 )

dr
(t )

uT (t )  dt
dr
(t )
dt
versor normal principal à trajectória

du T
(t )

u N (t )  dt

du T
(t )
dt
Material de apoio: cinemática
raio
de curvatura
v(t )
 (t )  
duT
(t )
dt



centro de curvatura rc (t )  r (t )   (t )uN (t )

 ( t )u N ( t )

r (t )
O

rc (t )
c
Material de apoio: cinemática

vector aceleração

2

dv
d r
a (t ) 
(t )  2 (t )
dt
dt



 a x (t )u x  a y (t )u y  a z (t )u z


dv x
d 2x
(t )  2 (t )
a x (t ) 
dt
dt


dv y
d2y

(t )  2 (t )
a y (t ) 
dt
dt


dv z
d 2z
(t )  2 (t )
a z (t ) 
dt

dt

componentes tangencial e normal, ou centrípeta



a (t )  aT (t )  a N (t )


 aT (t )uT  a N (t )uN
dv

aT (t )  dt (t )


2
v
a (t )  (t )
N

 (t )

Dimensões : LT-2
Unidades SI : m s-2
Material de apoio: cinemática
Movimento
curvilíneo geral

aT (t )

v (t )

a (t )

r (t )
O

a N (t )
Material de apoio: cinemática

movimento uniforme – norma da velocidade constante

aT (t )  0

movimento rectilíneo – direcção da velocidade constante

a N (t )  0
Material de apoio: cinemática

Movimento rectilíneo – requer apenas um eixo coordenado
com a direcção do movimento

v (t )



u x  uT  ur
independente do tempo



r (t )  x(t )u x  x(t )uT




v (t )  v(t )u x  vT (t )uT  vr (t )ur
a (t )  a(t )u  a (t )u
x
T
T

Material de apoio: cinemática


Movimento circular : r (t )  r , t - independente do tempo

y
v (t )
 velocidade angular

aT (t )

ds
d
a (t )

 (t ) 
(t )
a N (t )
dt
d
ds  r d


r (t )
x

ds
d
(t )  r
(t )  v(t )  r (t )
dt
dt
norma da velocidade
Dimensões : T-1
Unidades SI : rad s-1
Material de apoio: cinemática

 Movimento circular : r (t )  r , t - independente do tempo
y

 vector velocidade angular
v (t )

• norma :  (t )   (t )

r (t )
• direcção do eixo de rotação – eixo zz


perpendicular a r (t ) e v (t )

z
• sentido do eixo zz se movimento no sentido directo
sentido oposto ao eixo zz se movimento no sentido retrógrado




v (t )  v (t )u (t )   (t )  r (t )

r (t )  r  dr  0  vr  0
x
Material de apoio: cinemática


Movimento circular : r (t )  r , t - independente do tempo

vector aceleração angular

d
 (t ) 
(t )
dt


Dimensões : T-2
Unidades SI : rad s-2
relação entre as acelerações linear e angular







dv
d  (t )  r (t )  
a (t ) 
(t ) 
  (t )  r (t )   (t )  v (t )
dt
dt
• aceleração tangencial


aT (t )  aT (t )uT (t )
dv 

(t )uT (t )
dt


  (t )  r (t )
• aceleração normal


a N (t )  a N (t )u N (t )

v(t ) 2

(t )u N (t )
r


  (t )  v (t )
Material de apoio: cinemática


 cálculo de r (t ) a partir v (t )

1 condição inicial : r (t0 )
t 


r (t )  r (t0 )   v (t ' )dt '
t0


 cálculo de v (t ) a partir a (t )
t 


v (t )  v (t0 )   a (t ' )dt '

1 condição inicial : v (t0 )
t0


 cálculo de r (t ) a partir a (t )
t t'


 '
r (t )  r (t0 )  v (t0 )(t  t0 )    ' a (t ' ' )dt ' 'dt '
t0 t0

 '
2 condições iniciais : r (t0 ) ; v (t0 )
Material de apoio: cinemática

Movimento com velocidade constante: independente do tempo
t 


r (t )  r (t0 )   v (t ' )dt '


v (t )  v
t
t0

 t

v dt '  v  dt '  v t  t0 
t0
t0



r (t )  r (t0 )  v t  t0 






r (t )  r (t0 )  v t  t0   r (t )  r (t0 )  v t  t0 


r (t )  r (t0 )

r (t0 )
O

r (t )

S  vt
espaço percorrido é igual ao produto
da norma da velocidade pelo tempo
que demora a percorrê-lo
Material de apoio: cinemática

Movimento com norma da velocidade constante:

independente do tempo
v (t )  v(t )  v
t
dS
(t )  v(t )  S (t )  S (t0 )   v(t ' )dt '
t0
dt
t0vdt'  v t0dt '  vt  t 
t
t
0
S (t )  S (t0 )  vt  t0 

S  vt
espaço percorrido é igual ao produto
da norma da velocidade pelo tempo
que demora a percorrê-lo
Material de apoio: cinemática

Movimento com aceleração constante: independente do tempo


a (t )  a
t
t 


v (t )  v (t0 )   a (t ' )dt '

 t

adt '  a  dt '  a t  t0 
t0
t0
variação do vector velocidade é
igual ao produto da aceleração pelo
intervalo de tempo correspondente a
essa variação
t0



v (t )  v (t0 )  a t  t0 

 
v  a t
Material de apoio: cinemática
Movimento com aceleração constante: independente do tempo



a (t )  a
t t' 



r (t )  r (t0 )  v (t0 ' )(t  t0 )    ' a (t ' ' )dt ' 'dt '
t0 t0
t' 
 t'
 ' '
adt ' '  a ' dt ' '  a (t  t0 )
'
t0
t0

t
t0



 ' '
 t '
' t
1 2 1 2 '
a (t  t0 )dt '  a  t dt '  at0  dt '  a 2 t  2 t0  at0 t  t0 
t0
t0





1 2 1 2 '
r (t )  r (t0 )  v (t0 ' )(t  t0 )  a 2 t  2 t0  at0 t  t0 

condições iniciais conhecidas no mesmo instante de tempo: t0  t0'



1 
r (t )  r (t0 )  v (t0 )(t  t0 )  2 a t  t0 2
Material de apoio: cinemática

Movimento com aceleração constante: independente do tempo



1 2 1 2 '
r (t )  r (t0 )  v (t0 ' )(t  t0 )  a 2 t  2 t0  at0 t  t0 





1 
r (t )  r (t0 )  v (t0 )(t  t0 )  2 a t  t0 2
t0  t0'
 
 
 a e v0 paralelos - trajectória rectilínea com a direcção de a e v0
 
 a e v0 não paralelos - trajectória parabólica descrita no plano

 
formado por a e v0 e que passa por r0
 
 
  '
r0  r (t0 ) ; v0  v (t0 ) ou v0  v (t0 )

 
Movimento de projécteis: a  g independente do tempo
Material de apoio: cinemática

S z
Movimento relativo
vector posição relativa

rA (t )




rBA  rB  rA  rAB
B relativamente a A
A relativamente a B
A

rBA (t )

rB (t )
O
x
B
y
vector velocidade relativa




drBA 
v BA 
 vB  v A  v AB
dt
B relativamente a A
A relativamente a B
vector aceleração relativa

a BA
B relativamente a A




dvBA

 aB  a A  a AB
dt
A relativamente a B
Material de apoio: cinemática

Transformadas de Galileu
S’ y’
S
y
P
r , (t )

r (t )

rO, (t )
O’
z’
O
x
z
Velocidade de S’ relativamente
aS


constante 
x’
ro, (t )  Vt
t ,  t


,


r (t )  r (t )  Vt
 ,


v (t )  v (t )  V
 ,


a
(
t
)

a
(t )

Distâncias são invariantes
Intervalos de tempo são invariantes
Princípio da relatividade de Galileu
Leis da Mecânica são invariantes:
as mesmas em todos os referenciais inerciais
Todos os referenciais inerciais são equivalentes