UNIVERSIDADE DO ESTADO DE SANTA CATARINA

UNIVERSIDADE DO ESTADO DE SANTA CATARINA - UDESC
CENTRO DE CIÊNCIAS TECNOLÓGICAS – CCT
DEPARTAMENTO DE FÍSICA – DFIS
NOTA
Prova de Física Geral A – 25/04/2003
Profs. José Fernando Fragalli e César Henrique Wanke
2a
Nome do Aluno: ..................................................................................
1) Um bloco é lançado para cima, com velocidade inicial de 5,0 m/s, sobre uma
rampa de 45 de inclinação. O coeficiente de atrito cinético entre o bloco e a
rampa vale 0,30. Determine
a) a distância máxima atingida pelo bloco ao longo da rampa; (1,5)
b) a velocidade final com que ele chega de volta ao pé da rampa. (1,0)
2) Um bloco de massa 1,0 kg é lançado para cima com velocidade inicial de 2,0
m/s. No local em que ocorre este evento, o ar executa uma força de resistência
ao movimento do bloco. Consideremos que o módulo desta força seja
proporcional ao módulo da velocidade instantânea do bloco, e que a constante de
proporcionalidade seja igual a 2,5 Ns/m. Determine
a) o tempo que o bloco demora para atingir a altura máxima; (1,5)
b) O valor desta altura máxima. (1,0)
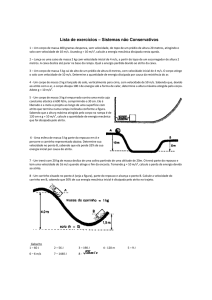
3) Uma partícula de massa m = 1,0 kg está sujeita a uma força associada com a
energia potencial cuja expressão matemática é U(x) = 3x2 – x3, onde x é dado em
metros e U em Joule. O gráfico de U(x) está mostrado abaixo.
a) Determine o sentido da força nos intervalos apropriados da variável x.
(0,5)
b) Determine analiticamente o ponto onde o equilíbrio é estável; da mesma
forma, determine analiticamente o ponto onde o equilíbrio é instável. (1,0)
c) Admitindo que em x = - 3,0 m a partícula esteja em repouso, determine a
sua velocidade em x = 3,0 m. (1,0)
4) Uma bolinha de massa 2,0 kg, amarrada a um fio de comprimento igual a 1,0
m executa um movimento circular num plano vertical. Determine
a) a velocidade da bolinha no ponto mais baixo da trajetória, para que ela
descreva um círculo completo. (1,5)
b) a tensão no fio quando ela passa no ponto mais baixo da trajetória. (1,0)
5) Um carrinho, partindo do repouso, desliza do alto de uma montanha russa,
com atrito desprezível. Ao chegar no sopé da montanha, ele percorre uma
distância d quando atinge a velocidade de 2,0 m/s. Admitindo que o coeficiente
de atrito entre o carrinho e o piso horizontal seja 0,50, determine
a) a distância d percorrida pelo carrinho; (1,5)
b) a energia dissipada pelo atrito. (1,0)


 dv

dU
a
F 
(T  U )  0
Fat    N
F ma
dt
dx
BOA SORTE!!!
W  T