1) Construa (utilizando régua, esquadro e transferidor) um triângulo

9º ano
Geometria
Junior
Aval. Trimestral
07/11/12
1) Construa (utilizando régua, esquadro e transferidor) um triângulo RST, retângulo
em S, com ângulo de 40° , no vértice R. Com uma régua, meça os catetos do triângulo
que você construiu. Anote as medidas no desenho, com base nessas medidas calcule
o seno , o cosseno e a tangente do ângulo R.
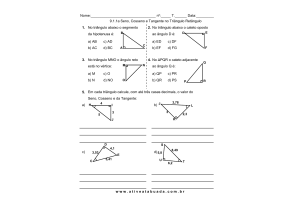
2) Calcule com base na figura, o seno, o cosseno e a tangente do ângulo de vértice
G.
3
G
4
3) Dado o triângulo ABC, escreva as razões indicadas:
ᵠ
a) senᵠ =
b) cos ᵠ =
c) tg ᵠ =
3
4
4) Construa um triângulo retângulo de catetos medindo 6 cm e 8 cm.
a) Meça os ângulos agudos desse triângulo.
b) Quanto mede a hipotenusa do triângulo?
c) Determine as razões trigonométricas de cada ângulo agudo.
5) Um papagaio, ou pipa, é preso a um fio esticado que forma um ângulo de 45° com
o solo. O comprimento do fio é de 100m. Determine a altura do papagaio em relação ao
solo. (Use seno 45° = 0,7071, cosseno 45° = 0,7071 e tangente 45° = 1)
6) Num triângulo retângulo, sabe-se que o cosseno de um ângulo ᵠ
vale 21/29.
Determine as menores medidas possíveis, em números inteiros, para os três lados do
triângulo.
7) Uma rampa plana, de 36 m de comprimento, faz ângulo de 30° com o plano
horizontal (chão). A que altura do chão fica uma pessoa que sobe toda a rampa?
8) Uma escada apoiada em uma parede, num ponto que dista 3 m do solo, forma,
com essa parede, um ângulo de 30°. Determine a distância a que o pé da escada se
encontra da parede.
9) Prove que qualquer diagonal de um paralelogramo o divide em dois triângulos
congruentes. Seja o paralelogramo ABCD e suas diagonais AC e BD.
Hipótese:
ABCD é um paralelogramo , AC e BD são diagonais
Tese : ∆ ADC ≈ ∆ CBA e ∆ ABD ≈ ∆ CDB
B
A
C
D
Demonstração
Afirmações
Justificativas
1)AC≈AC
1)
2)<DCA ≈ <CAB
2)
3)<DAC ≈ < ACB
3)
4)∆ADC ≈ ∆ CBA
4)
5) BD ≈ BD
5)
6) < ADB ≈ ........
6)
7) < ABD ≈ ..........
7)
8) ∆ ABD ≈ ∆ CDB
8)
Logo:
10) Determine as medidas dos ângulos internos do quadrilátero. Deixe registrado
como pensou.
72°