Capacitores - Sou Vestibulando

© QUESTÕES CORRIGIDAS – PROFESSOR Rodrigo Penna
1
QUESTÕES CORRIGIDAS
CAPACITORES
ÍNDICE
CAPACITÂNCIA .......................................................................................................................................................1
CAPACITOR DE PLACAS PLANAS PARALELAS .................................................................................................6
ENERGIA ARMAZENADA .......................................................................................................................................8
ASSOCIAÇÃO DE CAPACITORES ...................................................................................................................... 10
Capacitância
1.
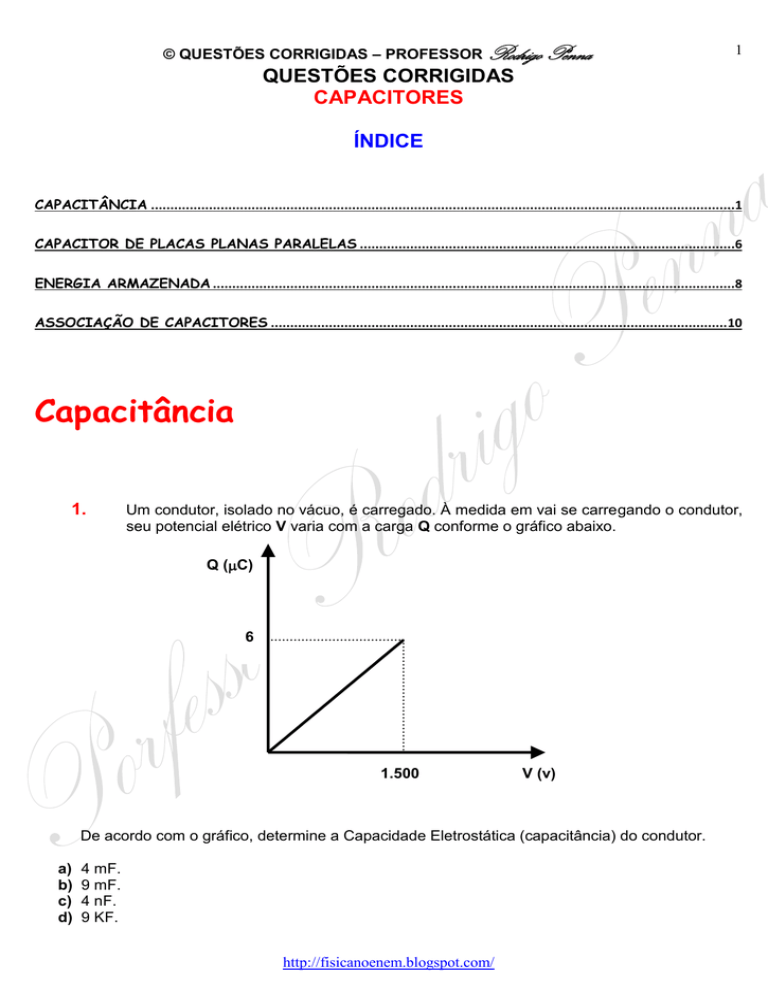
Um condutor, isolado no vácuo, é carregado. À medida em vai se carregando o condutor,
seu potencial elétrico V varia com a carga Q conforme o gráfico abaixo.
Q (C)
6
1.500
V (v)
De acordo com o gráfico, determine a Capacidade Eletrostática (capacitância) do condutor.
a)
b)
c)
d)
4 mF.
9 mF.
4 nF.
9 KF.
http://fisicanoenem.blogspot.com/
© QUESTÕES CORRIGIDAS – PROFESSOR Rodrigo Penna
CORREÇÃO
Como temos C 
2
Q
, do gráfico obtemos os valores. Atentar para a escala e para os
V
prefixos gregos.
6
6.
6
9
C
 10  4.10  4nF
1500
1500
GABARITO: C
2.
A)
B)
C)
D)
(PUC-2000) - Se dobrarmos a carga acumulada nas placas de um capacitor, a diferença
de potencial entre suas placas ficará:
multiplicada por quatro.
multiplicada por dois.
dividida por quatro.
dividida por dois.
CORREÇÃO
Q
. Como a Capacitância depende apenas da forma como o
V
2Q
Capacitor foi construído e neste caso não se altera, ao dobar a carga temos: C 
.
2V
A definição de Capacitância é: C 
GABARITO: B.
3.
Um capacitor de 6 F está ligado a uma bateria de 12V conforme o esquema
seguinte.
--
+
12V
Calculando o valor da carga elétrica armazenada no capacitor, encontramos:
a) 72C .
b) 72C.
c) 2C.
d) 2.10 6 C.
http://fisicanoenem.blogspot.com/
© QUESTÕES CORRIGIDAS – PROFESSOR Rodrigo Penna
3
CORREÇÃO
Aplicação direta da definição de Capacitância: Q = C.V .
Q = 6.10 - 6 x12 = 72. 10 – 6 C = 72C.
Tranqüilo...
OPÇÃO: A.
4.
Leia atentamente o texto abaixo, que fala sobre um tipo de memória de computador.
“Num chip de memória DRAM, cada bit é formado pelo conjunto de um transístor e um capacitor. O transistor
controla a passagem da corrente elétrica, enquanto o capacitor a armazena por um curto período. Quando o
capacitor contém um impulso elétrico, temos um bit 1 e quando ele está descarregado, temos um bit 0.
Quando falo em "capacitor", tenha em mente que não estamos falando em nada similar aos capacitores
eletrolíticos da placa-mãe. Os "capacitores" usados nos chips de memória são extremamente pequenos e simples,
basicamente dois pequenos blocos de metal ligados ao transistor, que conservam o impulso elétrico por apenas
uma fração de segundo.”
Site Guia do Hardware, http://www.guiadohardware.net/termos/memoria-ram , 18/05/09.
Com relação à utilização do capacitor no texto citado acima, podemos afirmar corretamente que finalidade de sua
utilização pode ser melhor explicada como:
a) armazenar energia.
b) fazer sintonização de radiofreqüência.
c) escrever informação digital.
d) fazer a correção da reatância indutiva.
CORREÇÃO
Pelo contexto da iformação, fica claro que o capacitor faz as vez de “caderno”, onde ocorre a “escrita digital”.
OPÇÃO: C.
http://fisicanoenem.blogspot.com/
4
© QUESTÕES CORRIGIDAS – PROFESSOR Rodrigo Penna
5.
(UFMG/11) A capacitância de um capacitor de placas paralelas é dada por C = Q/V , em
que Q é a carga em cada uma das placas e V , a diferença de potencial entre elas.
Desprezando-se os efeitos de borda, o campo elétrico entre as placas desse capacitor é
uniforme e de intensidade E = Q/εA, em que A é a área de cada uma das placas e ε é
uma constante.
1. Com base nessas informações, RESPONDA:
Que acontece com o valor da capacitância desse capacitor se a diferença de potencial entre as placas
for reduzida à metade?
2. Considere que um material isolante é introduzido entre as placas desse capacitor e preenche
totalmente o espaço entre elas. Nessa situação, o campo elétrico entre as placas é reduzido de um
fator κ , que é a constante elétrica do material.
EXPLIQUE por que, nessa situação, o campo elétrico entre as placas do capacitor diminui.
CORREÇÃO
Há 10 anos não vinha uma questão sobre Capacitores na UFMG... E já nem era cobrado antes
de se adotar o Enem, na primeira etapa de provas... http://www.slideshare.net/capitao_rodrigo/ufmg2a-etapa-2001-a-2010 . Tenho dúvidas quanto à necessidade de se ensinar este conteúdo no Ensino
Médio. Pelo visto, a própria UFMG também não dá muita importância, posto que a cobrança é rara.
Mas, também e contraditoriamente, não retira de vez do programa! Vai entender... Agora, vai ficar
mais mais 10 anos sem aparecer, ao invés de abrir espaço para dar mais tempo no estudo de outros
conteúdos, mais relevantes? Tira logo do programa, uai!
Embora seja básica, envolva o conceito de Capacitância, a 1ª pergunta pode levar a erros,
bobos. Escrevendo a fórmula de outro jeito: C = Q/V  Q = C.V . Façamos então o gráfico Carga Q
versus Voltagem V.
Q (C)
Note que, à medida que o capacitor vai
sendo submetido à maior voltagem, sua carga
aumenta. A capacitância é dada pela
inclinação da reta, constante: é uma função
Q4
do tipo y = a x. Ela é uma característica de
construção do capacitor, e depende de outros
Q3
A
fatores. A fórmula: C 
, onde C é a
Q2
d
capacitância, A a área das placas, d a
Q1
C
distância entre elas e  a permissividade do
isolante (0 seria a do vácuo), colocado entre
V1 V2 V3 V4
as placas. Veja na própria Wikipedia,
V (v)
desenhos e explicações.
A fórmula dada, do Campo Elétrico E,
entre as placas, pode levar a mais confusão, por quem
não sabe e fica inseguro... Veja o cálculo do peso.
P 2 P 3P
P  mg  g  

 ... . Se a massa dobra o
m 2 m 3m
peso dobra, se triplica o peso triplica e a gravidade
permanece constate... É o mesmo caso da
Capacitância, aqui.
No desenho acima, já ilustrei o dielétrico
(isolante) entre as placas do capacitor. A pergunta é sobre o efeito da introdução do dielétrico no
campo elétrico. Vejamos.
http://fisicanoenem.blogspot.com/
© QUESTÕES CORRIGIDAS – PROFESSOR Rodrigo Penna
5
Ao se introduzir um isolante, além do campo elétrico
entre as placas do capacitor, é criado um outro! As
moléculas sofrem um processo de polarização: se orientam,
conforme a figura, com separação de cargas! ( ver figura 10:
http://www.feiradeciencias.com.br/sala11/11_T02.asp ) As
positivas, no sentido do campo das placas e as negativas no
sentido contrário.
Atende ao detalhe das extremidades: tracejei, de
vermelho. À direita, o excesso de cargas positivas no
isolante. À esquerda, o contrário. Pela convenção da Física, o
campo elétrico “sai do mais e chega no menos”.

E
Temos, então, a soma de dois vetores, campos
elétricos: o antes, entre as placas, e o novo, devido ao isolante. O
resultado é um campo resultante, ERe s , menor que o anterior.
http://fisicanoenem.blogspot.com/
E
ERe s
E
© QUESTÕES CORRIGIDAS – PROFESSOR Rodrigo Penna
6
Capacitor de placas planas paralelas
(SP – C5 – H17) (FUVEST/94-modificado) Um capacitor é feito de duas placas
condutoras, planas e paralelas, separadas pela distância de 0,5 mm e com ar entre elas.
A diferença de potencial entre as placas é de 200 V. Substituindo-se o ar contido entre as
placas por uma placa de vidro, de constante dielétrica cinco vezes maior do que o do ar,
e permanecendo constante a carga das placas, qual será a diferença de potencial nessa
nova situação?
6.
a)
b)
c)
d)
8 V.
40 V.
1.000 V.
25.000 V.
CORREÇÃO
Temos que a capacitância de um Capacitor de placas planas e paralelas é dada por:
C
o A
d
. Na fórmula, C é a capacitância (F), o é a constante dielétrica do vácuo
(F/m), A área das placas (m2) e d a distância entre elas (m). Se, pelo problema, colocase vidro de constante 5 vezes maior, então a capacitância fica 5 vezes maior.
Da definição de Capacitância, temos: Q = C. V, onde Q é a carga elétrica e V a
voltagem. Se a capacitância aumenta sem variar a carga, teremos:
Q  5 C.
V
5
. A voltagem se reduz 5 vezes para manter a carga.
200 ÷ 5 = 40.
OPÇÃO: B.
7.
(SP – C5 – H17) (PUC-MG/99) Um capacitor de placas planas e paralelas é
totalmente carregado utilizando-se uma fonte de 12 volts em três situações
diferentes. Na situação A, ele permanece vazio. Em B, um dielétrico
preenche metade do volume entre as placas e, em C, o mesmo dielétrico
preenche todo o volume entre as placas.
Assim, com relação às cargas acumuladas, é CORRETO afirmar que:
http://fisicanoenem.blogspot.com/
© QUESTÕES CORRIGIDAS – PROFESSOR Rodrigo Penna
7
a) as cargas em A, B e C terão o mesmo valor.
b) A terá a maior carga e C, a menor.
c) A terá a menor carga e C, a maior.
d) B terá a maior carga e A, a menor.
CORREÇÃO
Sem utilizar nenhuma fórmula, quanto melhor o isolamento entre as placas, maior a
capacitância e maior a carga acumulada.
Com as fórmulas, a Capacitância depende do isolamento: C 
A
d
, constante , e
mantendo a voltagem constante a carga depende da capacitância: Q=CV.
OPÇÃO: C.
http://fisicanoenem.blogspot.com/
© QUESTÕES CORRIGIDAS – PROFESSOR Rodrigo Penna
8
Energia armazenada
8.
(SP – C5 – H17) (UFES/2001) Um capacitor ideal de placas planas paralelas é carregado
mediante a aplicação de uma d.d.p. entre suas placas. A distância entre as placas é
então duplicada, mantendo-se a mesma d.d.p. entre elas. Nessa nova situação, a carga
nas placas _________ e a energia eletrostática armazenada no capacitor __________.
Preencher CORRETAMENTE as lacunas, na seqüência em que aparecem na frase acima:
a) dobra - reduz-se à metade
b) não se altera - dobra
c) reduz-se à metade - reduz-se à metade
d) dobra - dobra
CORREÇÃO
Primeiramente, a Capacitância depende da distância entre as placas: C 
A
d
.
Dobrando a distância, a capacitância cai pela metade, já que são inversamente
proporcionais:
C o A

2 2d . Da definição de capacitância, Q=CV. Se a capacitância cai
pela metade, mantendo a voltagem constante, a carga também cai.
C.V 2
Finalmente, quanto à energia, para voltagem constante, prefiro: E 
. Vemos que
2
a energia é diretamente proporcional à capacitância, e também cai pela metade.
OPÇÃO: C.
9.
(SP – C5 – H17) (UFMG/94) Duas placas metálicas paralelas Q e P, isoladas, são
eletrizadas com uma carga de 1,0x10 – 7 C, uma negativamente e a outra, positivamente.
A diferença de potencial entre elas vale 100 V.
a) DETERMINE a energia elétrica armazenada nas placas.
http://fisicanoenem.blogspot.com/
9
© QUESTÕES CORRIGIDAS – PROFESSOR Rodrigo Penna
b) Considere que um resistor de 50  é usado para ligar uma placa à outra. À medida que as placas
se descarregam, a intensidade da corrente elétrica no resistor aumenta, diminui, ou não se altera?
JUSTIFIQUE sua resposta.
c) DETERMINE a quantidade total de calor liberado no resistor durante o processo de descarga das
placas.
CORREÇÃO
a) Aplicação direta de fórmula:
E
Q.V
2
1.107.100
E
 5,0.106 J
2
.
.
b) Podemos até desenhar, mas nem precisa...
À medida que o capacitor se descarrega, menos
menos corrente... Da fórmula, Q = CV, se a
capacitância se mantém constante, a voltagem
diminui quando a carga diminui. E, da Lei de Ohm,
i
carga,
V
R , menos voltagem, menos corrente.
c) Como a energia se conserva, toda a energia armazenada no capacitor será
convertida em calor por Efeito Joule: 5,0.10 – 6 J.
http://fisicanoenem.blogspot.com/
© QUESTÕES CORRIGIDAS – PROFESSOR Rodrigo Penna
10
Associação de capacitores
(SP – C5 – H17) (UFPE/2002) Quando dois capacitores, de capacitância C1 e C2, são
ligados a uma bateria, como mostrado na figura a seguir, adquirem cargas Q1 e Q2,
respectivamente. Sabendo que C•>C2, assinale a alternativa correta.
10.
a) Q1 > Q2
b) Q1 = 2 Q2
c) Q1 > Q2
d) Q1 < 2 Q2
CORREÇÃO
Questão até simples, para quem conhece a relação fundamental da Capacitância: Q =
CV. Já que a voltagem é a mesma – ligados na mesma bateria – a maior carga fica com
a maior capacitância.
OPÇÃO: A.
http://fisicanoenem.blogspot.com/