mat22005

Matemática 2
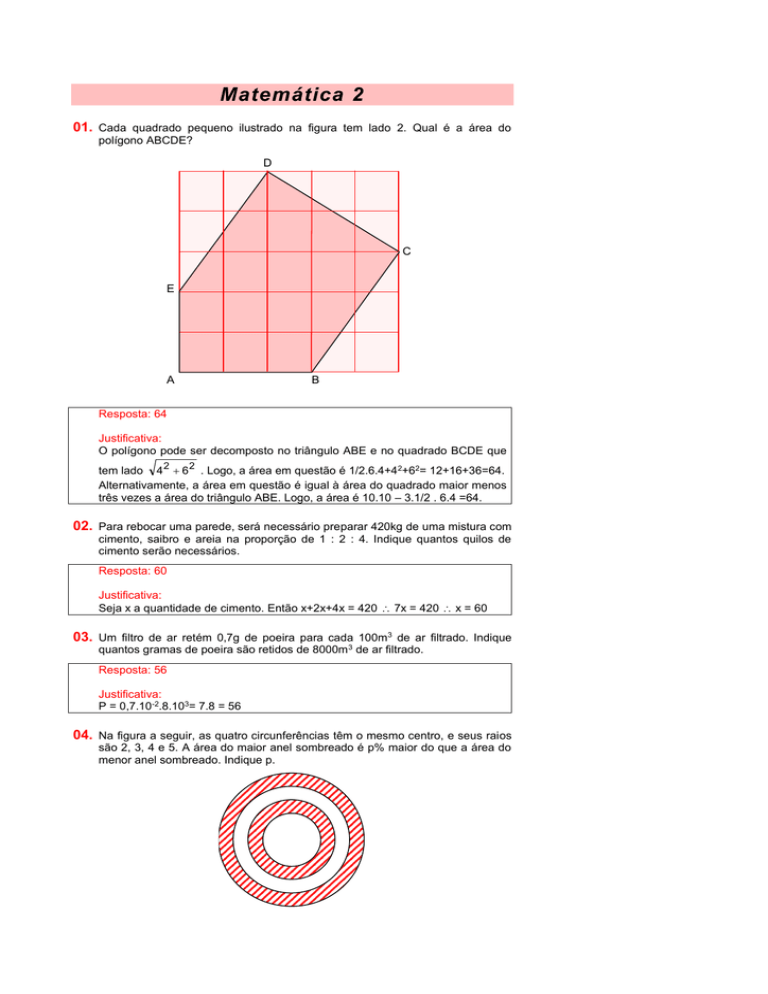
01. Cada quadrado pequeno ilustrado na figura tem lado 2. Qual é a área do
polígono ABCDE?
D
C
E
A
B
Resposta: 64
Justificativa:
O polígono pode ser decomposto no triângulo ABE e no quadrado BCDE que
tem lado 4 2  6 2 . Logo, a área em questão é 1/2.6.4+42+62= 12+16+36=64.
Alternativamente, a área em questão é igual à área do quadrado maior menos
três vezes a área do triângulo ABE. Logo, a área é 10.10 – 3.1/2 . 6.4 =64.
02. Para rebocar uma parede, será necessário preparar 420kg de uma mistura com
cimento, saibro e areia na proporção de 1 : 2 : 4. Indique quantos quilos de
cimento serão necessários.
Resposta: 60
Justificativa:
Seja x a quantidade de cimento. Então x+2x+4x = 420  7x = 420  x = 60
03. Um filtro de ar retém 0,7g de poeira para cada 100m3 de ar filtrado. Indique
quantos gramas de poeira são retidos de 8000m3 de ar filtrado.
Resposta: 56
Justificativa:
P = 0,7.10-2.8.103= 7.8 = 56
04. Na figura a seguir, as quatro circunferências têm o mesmo centro, e seus raios
são 2, 3, 4 e 5. A área do maior anel sombreado é p% maior do que a área do
menor anel sombreado. Indique p.
Resposta: 80
Justificativa:
Sejam A1, A2, as áreas dos anéis menor e maior, respectivamente. Temos
A 2 25  16 9

  1,8 e p = 80
A1
9  4
5
05. A figura abaixo ilustra a planificação de uma pirâmide de base quadrada com
lado medindo b e faces laterais formadas por triângulos isósceles com um lado
medindo b e os outros dois medindo a. Analise as afirmações.
a
b
0-0) A soma dos comprimentos das arestas da pirâmide é 4(a + b)
1-1) A área da superfície da pirâmide é b2 + 2b
a2 
b2
4
2-2) a > b/2
b2
b2
)
4
4
3-3) A altura da pirâmide é
(a 2 
4-4) O volume da pirâmide é
1 2
ba
3
Resposta: VVVVF
Justificativa:
0-0 e 2-2 são claramente verdadeiras.
1-1 e 3-3 são conseqüências do teorema de Pitágoras.
4-4 é falsa, pois a altura da pirâmide é menor do que a.
06. A figura a seguir ilustra a região sólida R de um cone reto, compreendida entre
duas seções meridianas que formam, entre si, um ângulo . Indique o volume
de R, sabendo que a altura do cone é 5, o raio de sua base é 3 e  = 2
radianos.
Resposta: 15
Justificativa:
Volume de R = 1/3 (altura x área da base) = 1/3 . 5 . 1/2.2 . (32) = 15
07. Dentre os retângulos com um vértice na origem de um sistema de coordenadas
cartesianas xOy, um vértice no semi-eixo positivo das abscissas, outro no semieixo positivo das ordenadas e o quarto vértice na reta 9x+5y=45, existe um que
tem a maior área. Assinale o perímetro deste retângulo.
Resposta: 14
Justificativa:
O vértice do retângulo que está sobre a reta situa-se no primeiro quadrante.
Se o ponto no eixo das abscissas tem coordenada x, então, a altura do
retângulo é (45-9x)/5, e sua área é x(45-9x)/5 que tem valor máximo para
x=(0+45/9)/2=5/2. A altura do triângulo de área máxima é 9-9/5.5/2=9/2 e
seu perímetro é 2(5/2+9/2)=14.
08. Os pontos F1 e F2 são os focos de uma elipse cujo eixo maior mede 10 e cujo
eixo menor mede 6. Indique a soma dos perímetros dos triângulos ACF1, BCF2
e F1F2D.
B
A
C
F2
F1
D
Resposta: 38
Justificativa:
A soma pedida é igual a BF2+BF1+AF2+AF1+DF2+DF1+F1F2 = 3.10 + F1F2.
2
F1F2
FF 
Temos  1 2  +32 = 52 e 2 = 4. A soma pedida é, portanto, 3.10 + 8 =
 2 
38
09. Determine a abscissa x0 do ponto da reta y = 7x – 3 que está a menor
distância do ponto (1,3). Indique 100x0.
Resposta: 86
Justificativa:
Justificativa: O quadrado da distância entre um ponto (x, 7x – 3) da reta e o
ponto (1,3) é (x-1)2 + (7x – 3 – 3)2 = 50x2 – 86x + 37, que tem mínimo para
x0 = 86/100 = 0,86.
10. Na ilustração abaixo, temos um cone reto com geratriz 10cm e raio da base
6cm, assim como sua planificação. Uma formiga, inicialmente no ponto A da
base do cone, poderá atingir o ponto B, caminhando sobre a superfície do cone.
Se o ponto B é o ponto médio de uma geratriz VC e o arco AC da base mede
5  /9 radianos, determine a menor distância d que a formiga percorrerá para
alcançar o ponto B. Indique d2.
Resposta: 75
Justificativa:
O arco AC na circunferência da base mede 5  /9.6 = 10  /3. Na
planificação, o ângulo AVC mede (10  /3)/10 =  /3 radianos. Usando a
Lei dos cosenos, temos d2 = 102 + 52 – 2.10.5cos(  /3) = 125 – 50 = 75.
11. O triângulo ABC ilustrado a seguir tem os lados AB e AC medindo 6 e 5,
respectivamente, e o ângulo BAC medindo 120 o . Determine o volume V do
sólido obtido quando o triângulo ABC gira em torno de uma reta contendo o
lado AC. Indique V/.
B
A
C
Resposta: 45
Justificativa:
O sólido é obtido retirando-se, de um cone de raio da base 6sen 60o = 3 3
e altura 5 + 6cos 60o = 8, um cone de mesmo raio da base e altura 3. O
sólido tem volume V = (3
3 )2(8-3)/3 = 45.
12. Seja G o baricentro do triângulo ABC e sejam I e J os pontos médios dos
segmentos AG e BG. Analise as afirmações a seguir.
C
K
L
G
I
A
J
B
0-0) O segmento IJ é paralelo ao lado AB.
1-1) O segmento KL mede metade do lado AB.
2-2) Os segmentos IJ e KL são congruentes.
3-3) Os segmentos IJ e KL são paralelos.
4-4) IJKL é um paralelogramo.
Resposta: VVVVV
Justificativa:
Como I e J são os pontos médios de AG e BG, respectivamente, segue que
IJ é paralelo a AB e mede metade de AB. Analogamente, LK é paralelo a AB
e mede metade de AB. Portanto, 0-0, 1-1, 2-2 e 3-3 são verdadeiros. Como
IJ e KL são paralelos e congruentes, temos que IJKL é um paralelogramo.
13. Quantos ângulos triedros ficam determinados por três retas não-coplanares e
concorrentes em um mesmo ponto?
Resposta: 8
Justificativa:
Temos seis semi-retas com origem na interseção das três retas. Para a escolha
da primeira semi-reta, temos seis possibilidades, da segunda, quatro
possibilidades, e da terceira, duas possibilidades, resultando em 6.4.2/6 = 8
ângulos triedros (observe que, permutando-se as três semi-retas, o triedro fica
inalterado).
As informações abaixo referem-se às duas questões seguintes:
Seja ABC um triângulo isósceles com AB = AC = 2BC e BC = 10 15 . Seja I o
incentro do triângulo, e D o ponto onde a circunferência inscrita intercepta o lado AB.
A
D
I
B
C
14. Determine o raio da circunferência inscrita no triângulo ABC.
Resposta: 15
Justificativa:
A altura do triângulo ABC mede
AB 2  BC / 22  4BC2  BC2 / 4  15BC / 2
e
sua
área
mede
BC.( 15 .BC/2)/2 = BC2 15 / 4 . Portanto, se r é o raio da circunferência
inscrita ao triângulo ABC, temos (BC+AB+AC).r/2 = BC2 15 / 4 ou 5BC.r/2 =
BC2 15 / 4 e segue que r = BC 15 /10 =
15
15 = 15.
15. Calcule BD e indique BD2/5.
Resposta: 75
Justificativa:
Temos BD2 = BI2 – r2 = r2 + (BC/2)2 – r2 = (BC/2)2 = BC2/4 = (10 15 )2/4 =
5.75. Alternativamente, tem-se que BD = BE = BC/2, onde E é o ponto de
tangência da circunferência ao lado BC.
16. Na ilustração a seguir, os pontos P1, P2, P3 e P4 são pontos médios das arestas
VA1, VA2, VA3 e VA4. Se a pirâmide VA1A2A3A4 tem volume 480, qual o volume
da pirâmide VP1P2P3P4 ?
V
P3
P4
P1
P2
A3
A4
A1
A2
Resposta: 60
Justificativa:
As pirâmides são semelhantes com razão de semelhança 2. Logo, o volume
de VP1P2P3P4 é 480/23 = 60.
17. Considerando z = (1 + 3 i)/2, analise as afirmações a seguir:
0-0) A forma trigonométrica de z é cos(/3) +isen(/3).
1-1) z6 = 1
2-2) Os afixos de z, z3, z5 são vértices de um triângulo eqüilátero.
3-3) Os afixos de z, z2, z4 e z5 são vértices de um quadrado.
4-4) z3 = 1.
Resposta: VVVFF
Justificativa:
z forma com o semi-eixo positivo das abscissas um ângulo  tal que sen  =
3 /2 e cos  = ½ logo,  = /3 e z = cos(/3) +isen(/3). Daí z3 = cos(3/3)
+isen(3/3) = -1 e z6 = 1. Segue que 0-0 e 1-1 são verdadeiras e 4-4 é falsa.
Temos também que 1, z, z2, z3, z4, z5 são vértices de um hexágono regular.
A distância entre z3 e z e entre z3 e z5 é dada por
9/43/4  3 ; a
z5
distância entre z e
é 2. 3 /2 = 3 . Portanto, os afixos de z, z3 e z5
formam um triângulo eqüilátero; logo, 2-2 é verdadeira. A distância entre z e
z2 é 1 e entre z e z5 é 3 ; logo, os afixos de z, z2, z4, z5 não são vértices de
um quadrado e 3-3 é falsa.
18. A ilustração abaixo representa parte do gráfico de um polinômio cúbico p(x)
com coeficientes reais e coeficiente dominante positivo. O gráfico do polinômio
passa pelos pontos (-1,0) e (2,0).
y
-3
-2
0
-1
1
2
3
x
-50
-100
-150
-200
Considerando as informações acima, analise as alternativas a seguir:
0-0) p(x) admite exatamente duas raízes reais.
1-1) p(x)  100, para todo x real.
2-2) p(x) é divisível por x2 – x – 2.
3-3) p(x) admite uma raiz complexa não real.
4-4) p(x)  -250, para todo x real.
Resposta: FFVFF
Justificativa:
Como p(x) é ilimitado para x positivo, temos que p(x) admite três raízes
reais; portanto, 0-0, 1-1 e 3-3 são falsas. Como –1 e 2 são raízes de p(x),
temos que p(x) é divisível por (x + 1)(x – 2) = x2 – x – 2; logo, 2-2 é
verdadeira. Para x negativo, p(x) não admite valor mínimo.
19. Encontre a raiz racional x da equação
x3
x
2 1

x3
x
2x

x2
x2  x
0
e indique -30x.
Resposta: 50
Justificativa:
Multiplicando a igualdade por (x – 1)x(x + 1), obtemos x(x + 3) + (x + 1)(x –
3) + (x – 1)(x + 2) = 0 que se simplifica como 3x2 + 2x – 5 =0 que tem raízes
x = (-2  64 )/6 = -5/3 e 1. x = 1 não é raiz da equação e
–30.(-5/3) = 50.
20. Um cilindro reto de raio da base 8cm e altura 30cm está inscrito em uma
superfície esférica. Calcule o volume V, em cm 3, da região da esfera exterior ao
cilindro e indique a soma dos dígitos do inteiro mais próximo de V. Aproxime 
por 3,14.
Resposta: 14
Justificativa:
82  152  17 cm, e o volume da região considerada
= 14540,29.
O raio da esfera mede
é
4173/3
-
.82.30
21. Na ilustração a seguir, a circunferência passa pelos vértices A e B do quadrado
ABCD e é tangente ao lado CD. Se o quadrado tem lado 12, indique o diâmetro
da circunferência.
D
C
A
B
Resposta: 15
Justificativa:
Considere o triângulo com vértices no centro da circunferência, no vértice A
e no ponto médio de AB. Se r é o raio da circunferência, temos (12-r)2+62 = r2
que se simplifica como 180-24r = 0 e daí r = 7,5.
22. Na figura abaixo, ABCD é um quadrado de lado medindo 12, e ABE e CDF são
triângulos equiláteros. Indique o inteiro mais próximo da área do quadrilátero
EGFH. (Obs.: Use a aproximação
3  1,73.)
D
C
E
G
H
F
A
B
Resposta: 22
Justificativa:
Solução: EGFH consiste de dois triângulos equiláteros congruentes: EGH e
FGH. O ângulo BCH mede 30o e, portanto, cos30o =6/CH; logo, CH=4 3 e
o lado do triângulo EGH mede 12-4 3 . A área do quadrilátero EGFH mede
2.(12-4 3 )2 3 /4=8(12-6 3 ) 3 = 96
3 -144  22,08.
23. As expressões numéricas x-5, 2x-9, 3x-13 e 4x-3 podem ser reordenadas de
modo que a soma das duas primeiras seja 30, e a soma das duas últimas seja
60. Qual o maior dos quatro números?
Resposta: 45
Justificativa:
A soma das quatro expressões é 90. Portanto, x-5+2x-9+3x-13+4x-3=90 e
daí 10x=120 e x=12. Os números são 7, 15, 23 e 45.
24. Na ilustração abaixo, os segmentos AB e EF são paralelos. Determine a soma
S, em graus, dos ângulos indicados com vértices nos pontos B, C, D e E.
Indique S/10.
B
A
C
D
E
F
Resposta: 54
Justificativa:
Seja G o pé da perpendicular a AB, passando por A . O polígono ABCDEG
tem a soma dos ângulos internos dada por (6-2).180o=4.180º A soma dos
ângulos indicados é 4.180o-180o=3.180o=540º.
25. O círculo da ilustração abaixo tem raio 6, o ângulo BOC mede 60o e os ângulos
AOB e COD medem 30o. Qual o inteiro mais próximo da área da região
colorida? (Obs.: use a aproximação   3,14.)
O
A
D
B
C
Resposta: 19
Justificativa:
A área do setor OABCD é 1/3..62=12 e a do setor OBC é 1/6. .62=6. O
triângulo OAD tem área 62.sen120o/2=9 3 e o triângulo OBC tem área
62 3 /4=9 3 . A área da região colorida é 12-9 3 -(6-9 3 )=6
18,84.

26. O poliedro convexo que inspirou a bola de futebol é formado de faces regulares
pentagonais e hexagonais. O número total de vértices é 60, e o de arestas é 90.
Quantas são as faces hexagonais?
Resposta: 20
Justificativa:
Da relação de Euler obtemos 60 – 90 + F = 2 e F = 32. Se x é o número de
faces hexagonais, temos que existem 32 – x faces pentagonais e, contando
o número de arestas, temos 6x + 5(32 – x) = 2.90, que equivale a x = 180 –
160 = 20.
27. Na ilustração a seguir, o triângulo ABC é eqüilátero, a circunferência maior está
inscrita no triângulo a as duas menores são tangentes à maior e a dois lados do
triângulo. Se o triângulo tem lado medindo 18, qual o maior inteiro menor que a
área da região colorida? (Dado: use as aproximações
A
C
B
Resposta: 36
3  1,73 e   3,14.)
Justificativa:
A circunferência maior tem raio 1/3.18. 3 /2 = 3 3 . As circunferências
menores estão inscritas em triângulos eqüiláteros de altura 9 3 - 2(3 3 ) =
3 3 ; logo, têm raio 1/3.3 3 =
3 . A soma das áreas limitadas pelas
circunferências é ((3 3
33  36,51.
2)
)2
+ 2.
3
= 33 e a área colorida é 182 3 /4 –
28. Na ilustração abaixo, o ponto P está no interior do triângulo ABC, e por P são
traçadas paralelas aos lados AB, AC e BC que interceptam estes lados nos
pontos D, E, F, G, H e I. Se ABC é eqüilátero de lado 100, DE = 25 e FG = 45,
qual a medida de HI?
C
G
H
P
I
A
D
F
E
B
Resposta: 30
Justificativa:
Os triângulos ABC, DEP, FGP e HIP são todos semelhantes. Portanto,
DE/AB + FG/BC + HI/AC = DE/AB + PF/AB + PI/AB = (EB + DE + AD)/AB =
1. Daí 25/100 + 45/100 + HI/100 = 1 e HI = 30.
29. Na ilustração abaixo, ABCD é um quadrado, e EFGHIJ é um hexágono regular
com os vértices E, G, H e J, nos lados AB, BC, CD e DA do quadrado,
respectivamente. A diagonal FI do hexágono está contida na diagonal AC do
quadrado. Se o quadrado tem lado 100, qual o inteiro mais próximo do lado do
hexágono? (Dado: use a aproximação: cos 15o  0,96.)
D
H
C
I
G
J
F
A
E
B
Resposta: 52
Justificativa:
Seja O o centro do hexágono (ou do quadrado), e seja K o pé da
perpendicular por O ao lado AB. Temos que o triângulo KOE tem o ângulo
EOK medindo 60o – 45o = 15o ; daí cos 15o = OK/OE e OE = 50/0,96  52,08.
30. Um tablete de doce de goiaba tem a forma de um paralelepípedo reto retângulo
de dimensões 10cm, 8cm e 6cm. O tablete foi embrulhado em papel celofane e
dividido em cubos de aresta 1cm. Analise as afirmações abaixo, a partir destes
dados:
0-0) Existem 480 cubos de aresta 1cm.
1-1) Existem 245 cubos sem qualquer face coberta pelo papel.
2-2) Existem 208 cubos com exatamente uma face coberta pelo papel.
3-3) Existem 36 cubos com exatamente duas faces cobertas pelo papel.
4-4) Existem 8 cubos com exatamente três faces cobertas pelo papel.
Resposta: VFVFV
Justificativa:
O número de cubos é 10.8.6 = 480, logo, 0-0 é verdadeira. O número de
cubos sem qualquer face coberta de papel é (10 - 2)(8 - 2)(6 - 2) = 192; logo,
1-1 é falsa. O número de cubos com uma face coberta pelo papel é 2(8.6 +
8.4 + 6.4) = 208; logo, 3-3 é verdadeira. O número de cubos com duas faces
cobertas de papel é 72; logo, 3-3 é falsa; existem oito cubos com três faces
cobertas de papel, o que torna 4-4 verdadeira.
31. Um jogador esteve em três casas de apostas durante uma noite: na primeira,
ele dobrou a quantia que possuía ao chegar e, posteriormente, gastou R$
30,00. Na segunda, ele triplicou a quantia que tinha ao chegar e,
posteriormente, gastou R$ 54,00 e, na terceira, ele quadruplicou a quantia que
tinha ao chegar, então gastou R$ 72,00 e observou que lhe restavam R$ 48,00.
Qual a quantia, em reais, que ele tinha ao chegar à primeira casa de apostas?
Resposta: 29
Justificativa:
Ao chegar à terceira casa de apostas, ele tinha (72 + 48)/4 = 30 reais; ao
chegar à segunda casa de apostas ele tinha (30 + 54)/3 = 28 reais e, ao
chegar à primeira casa, ele tinha (28 + 30)/2 = 29 reais.
32. No primeiro semestre de 2003, a indústria X teve um faturamento 20% superior
ao da indústria Y. No primeiro semestre de 2004, os faturamentos das
indústrias X e Y cresceram 20% e 50%, respectivamente. No primeiro
semestre de 2004, o faturamento da indústria X foi inferior em p% ao
faturamento da indústria Y. Indique 10p.
Resposta: 40
Justificativa:
Se y denota o faturamento da indústria Y no primeiro semestre de 2003,
então, o faturamento da indústria X, no mesmo período, foi de 1,2y. No
primeiro semestre de 2004, os faturamentos das indústrias X e Y foram de
1,2.1,2y=1,44y e 1,5y, respectivamente. Portanto, o faturamento da indústria
X foi inferior em (0,06./1,5).100%=4% ao faturamento da indústria Y.