Irracionalidade e Trascendencia dos números π ee - Imecc

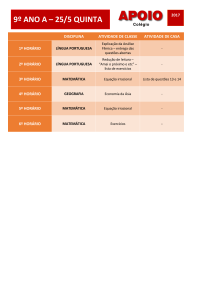
Irracionalidade e Trascendencia dos números
Leandro Cedeño Hernandes, RA 044651
María Eugenia Martin, RA 039885
MM/MA 445 Aneis e Corpos
Imecc-Unicamp
1 de outubro de 2007
1
π
e
e
Sumário
1 Alguns fatos históricos sobre os números
3
2 Irracionalidade e Transcendencia
6
3 Os números algébricos formam um corpo
7
4 Números irracionais
9
1.1
1.2
π e e.
O número π . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
O número e. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3
4
4.1
4.2
O número e é irracional . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
O número π é irracional . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
4.3
Outros números irracionais
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
5 Números transcendentes
13
5.1
O número e é transcendente . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
5.2
O número π é transcendente . .
5.2.1 Polinômios simétricos .
5.2.2 Demonstração . . . . . .
Outros números transcendentes
5.3
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
2
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
14
14
16
18
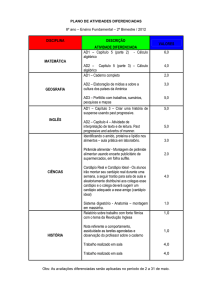
1
Alguns fatos históricos sobre os números
1.1
O número
π
e
e.
π.
A história do número π provavelmente começa com a tentativa de calcular o perímetro ou a área
de um círculo conhecendo-se seu raio. Os papiros egípcios de 2000 a.C. já apresentam indícios da
tentativa de se calcular o valor de π , denido comoo quociente do perímetro com o diâmetro de uma
2
= 3, 1604 . . . , um valor bem próximo do atual
circunferência, com valores para o mesmo de 16
9
3, 1415 . . . . Outras estimativas Babilônicas e Egípcias estimam valores como 3, 3 81 , 3 17 . Também
implícito na Bíblia, encontramos o valor 3 para π.
O interesse puramente matemático em π data da Grécia Antiga, onde se investigava o problema
da quadratura do círculo, que consiste em construir um quadrado de mesma área que um círculo
dado, questão que foi resolvida, milhares de anos depois, por Lindemann em 1822 ao demonstrar a
transcendência do número π , que implicava em resposta negativa.
Arquimedes de Siracusa (287-212 a.C.), da Grécia Antiga, conseguiu uma boa aproximação para
π através da inscrição e circunscrição de polígonos de 96 lados em uma circunferência, conseguindo
10
3 71
< π < 3 17 .
Porém, seu método de inscrição e circunscrição de polígonos regulares de cada vez mais lados
logo apresentou limitações por sua convergência demorada para π , e logo surgiram outros algorítmos
mais ecientes para o cálculo de π e a primeira expansão innita, devida a François Viéte(15401603):
v
s
r s
r u
r
u
2
1 1 1 1t1 1 1 1 1
=
+
+
+
···,
π
2 2 2 2 2 2 2 2 2
e logo vieram outras, como a devida a John Wallis(1616-1703):
π
2 · 2 · 4 · 4 · 6 · 6 · 8 · 8···
=
.
2
1 · 3 · 3 · 5 · 5 · 7 · 7 · 9···
A expansão de π na forma de fração contínua foi obtida pela primeira vez por Lord Brouncker(16201684):
π=
4
1+
1
9
2+ 2+...
.
Em 1971 James Gregiry(1638-1675) mostrou que:
Z x
dx
x3 x5 x7
arctan x =
=
x
−
+
−
+ ···
2
3
5
7
0 1+x
evaluando em x = 1 temos:
π
1 1 1
= 1 − + − + ···,
4
3 5 7
uma fórmula que foi descoberta tambémqindependentemente em 1674 por Leibniz(1646-1716).
Usando a série de Gregory com x =
1
3
temos:
π
1
1
1
1
= √ (1 −
+ 2
− 3
+ ···)
6
3·3 3 ·5 3 ·7
3
3
Com essa expansão, E. Halley obteve 71 dígitos corretos para π.
Com expansão em arcsin, Newton obteve 15 dígitos corretos de π , tal expansão é:
√
3· 3
1
1
1
1
π=
−
− 2 9 − · · · ).
+ 24( −
5
7
4
12 5 · 2
28 · 2
7 ·2
John Machin(1680-1752) obteve uma fórmula que leva o seu nome:
π
1
1
= 4 arctan( ) − arctan(
)
4
5
239
Duas identidades importantes e bonitas, devidas a Euler (1707-1783) são:
∞
∞
n=1
n=1
π2 X 1
π4 X 1
=
e
=
.
6
n2 90
n4
Com o passar do tempo, com o advento dos computadores, os dígitos de π foram calculados na
casa dos milhares e depois dos milhões, usando novas identidades descobertas nesse período.
Várias questões depois foram levantadas à respeito de π , como por exemplo se π é normal, ou
seja, se a sequência de seus innitos dígitos é uniformemente distribuída, ou seja: 10% de aparições
para cada dígito diferente, 1% de aparição para cada dezena diferente como 45, e assim por diante.
Até agora, os cálculos computacionais conrmam essa conjectura.
1.2
O número
e.
O número de Euler, assim chamado em homenagem ao matemático suíço Leonhard Euler, é a base
dos logaritmos naturais.
O número e, é denido como o número k tal que a área abaixo do gráco da função f (x) = x1
e acima do eixo x, para 1 ≤ x ≤ k , é igual a 1. Isto é, o número e pode ser denido como o único
número k > 0 tal que:
Z k
dt
= ln k .
1=
1 t
A primeira aparição da constante foi descoberta por Jakob Bernolli, quando tentava encontrar
um valor para a seguinte expressão (muito comum no cálculo de juros compostos):
1 n
e = lim 1 +
,
n→∞
n
e vale aproximadamente 2, 718281828459045235360287 · · · .
O número e também pode ser escrito como a soma da série innita:
e=
∞
X
1
1
1
1
1
1
= + + + + + ···.
n!
0! 1! 2! 3! 4!
n=0
Conjecturou-se que o número e é normal, ou seja, tem os seus innitos dígitos decimais igualmente distribuídos.
Ele aparece, junto com outras constantes fundamentais, na identidade de Euler:
eiπ + 1 = 0.
O desenvolvimento de e em frações contínua pode ser escrito como:
4
1
e=2+
1+
1
2+
1
1+
1+
1
1
1
4+ ...
A função f (x) = ex , solução da equação diferencial ẋ = x, desempenha um papel de suma
importância no cálculo diferencial e integral.
A escolha da letra e para representar a constante acima deve-se a Leonhard Euler e a primeira
aparição dessa notação ocorreu na publicação Eulers Mechanica em 1736. As verdadeiras razões
para essa escolha são desconhecidas, mas especula-se que seja porque e é a primeira letra da palavra
exponencial.
5
2
Irracionalidade e Transcendencia
a
b
Denição 1 Um número da forma , com a e b inteiros e b não nulo, é chamado de
racional. Um
número é irracional quando não é racional.
√
Vamos mostrar que existem números irracionais provando que 2 não é racional.
√
√
a
Se 2 fosse racional, ou seja, 2 = , com mdc(a, b) = 1, teríamos:
b
√
2=
a
a2
⇒ 2 = 2 ⇒ 2b2 = a2 ,
b
b
ou seja, a2 é par, logo a também é par, então podemos escrever a na forma a = 2k com k inteiro.
Logo
(2k)2
2=
⇒ 4k 2 = 2b2 ⇒ 2k 2 = b2 ,
b2
ou seja, b2 é par o que implica que b também é par, mas isso é um absurdo pois supomos que
√
√
a
mdc(a, b) = 1. Logo 2 não pode ser representado na forma , portanto temos que 2 não é
b
√
racional, ou seja, 2 é um número irracional. Assim provamos a existência dos números irracionais.
Denição 2 Um número real a é dito algébrico se é solução de alguma equação polinomial do tipo:
an xn + an−1 xn−1 + · · · + a1 x + a0 = 0,
sendo que os coecientes a0 , a1 , . . . , an são todos inteiros e a0 6= 0. Dizemos que um número a é
transcendente quando não for algébrico.
√ 10
√ √
Todas as raizes tais como
2,
3, 4 7 são claramente números algébricos, e também combiq
p
√
√
√
3
4
nações complicadas como 3 + 5 + 1 + 2 + 5 6 são algébricas. Também existem algébricos
√
complexos, por exemplo, i = −1 e −i pois são raízes de x2 + 1 = 0.
6
3
Os números algébricos formam um corpo
Vamos agora estabelecer que os números algébricos formam um corpo, ou mais especicamente
um subcorpo do corpo dos números reais. Este fato será usado posteriormente. Para tanto, vamos
demonstrar os seguintes resultados:
Lema 3 O simétrico −a de um número algébrico a, é algébrico.
Se a é algébrico, então ele é raiz de uma equação do tipo an xn + an−1 xn−1 +
· · · + a1 x + a0 = 0 , portanto −a é raíz da equação:
Demonstração.
(−1)n an xn + (−1)n−1 an−1 xn−1 + · · · + (−1)a1 x + a0 = 0
Lema 4 O inverso a−1 de um número algébrico ,com a não nulo, é algébrico.
Se a, não nulo, satisfaz a equação an xn + an−1 xn−1 + · · · + a1 x + a0 = 0, então
satisfaz a equação:
a0 xn + a1 xn−1 + · · · + an−1 x + an = 0.
Demonstração.
−1
a
Vamos necessitar de um fato sobre formas lineares com coecientes racionais.
Denição 5 Uma
forma linear com coecientes racionais é uma expressão da forma:
X = q1 x 1 + · · · + qn x n ,
onde q1 , . . . , qn são todos racionais. Os xi´s são chamados indeterminadas.
Lema 6 Dadas n + 1 formas lineares
X1 = q11 x11 + · · · + qn1 xn1
..
.
Xn+1 = q1 x1 + · · · + qn xn
elas são linearmente dependentes sobre os racionais, isto é, existem r1 , ..., rn+1 ∈ Q, com pelo menos
um ri distinto de zero, tais que
r1 X1 + · · · + rn+1 Xn+1 = 0.
Demonstração.
Substituindo os Xi´s por suas expressões dadas no enunciado do Lema, vemos que
r1 X1 + · · · + rn+1 Xn+1 = 0
estará satisfeita se os ri´s forem as soluções do sistema de equações lineares, (n equações com n + 1
incógnitas)
q11 r1 + q21 r2 ... + qn+1 rn+1 = 0
..
.
q1n r1 + q2n r2 ... + qn+1,n rn+1 = 0.
Pode-se mostrar que sistema acima tem soluções racionais r1 , ..., rn+1 uma vez que os coecientes
do sistema são também racionais.
7
Lema 7 A soma de dois números algébricos é algébrico.
Demonstração.
Sejam a e b números algébricos. Logo, existem equações polinomiais:
xn + an−1 xn−1 + · · · + a1 x + a0 = 0
m
x + bm−1 x
m−1
+ · · · + b1 x + b0 = 0
(1)
(2)
com coecientes racionais (a equação da denição de número algébrico tem coecientes inteiros, as
equações acima são obtidas dividindo-se a equação original pelo coeciente líder), tais que a seja
raiz de (1) e b seja raíz de (2). De (1) obtemos:
an = −an−1 an−1 − · · · − a1 a − a0 ,
(3)
isto é an está expresso como uma combinação linear de 1, a, ..., an−1 , usando coecientes racionais.
Multiplicando-se (3) por a e substituindo-se o an , obtido na expressão pelo seu valor dado em
(3), obtemos an+1 expresso como combinação linear dos mesmos 1, a, ..., an−1 usando-se também
coecientes racionais. E assim, sucessivamente, todas as potências aj , para j ≥ n , são expressas
como combinações lineares de 1, a, ..., an−1 usando-se coecientes racionais.
De modo análogo, podemos exprimir as potências bk , para k = m, m+1, . . . , como combinações
lineares de 1, b, ..., bm−1 usando-se coecientes racionais.
Nosso objetivo será mostrar que a + b satisfaz uma equação polinomial de grau mn com coecientes racionais, implicando então que a + b seja algébrico. Com isso em vista considere os mn + 1
números
1, a + b, (a + b)2 , . . . , (a + b)mn
(4)
Desenvolvendo as várias potências, e usando-se o que se viu acima sobre a representação de
potências aj , j ≥ n e bk , k ≥ m, obtemos que os números em (4) podem ser expressos como
combinações lineares dos mn números aj bk ,0 ≤ j ≤ n − 1, 0 ≤ k ≤ m − 1, usando-se coecientes
racionais. Agora, aplicamos o Lema acima: os Xi´s são os mn + 1 números de (4), os xi´s são os mn
números aj bk . Logo, existem racionais r0 , r1 , ..., rmn tais que
r0 + r1 (a + b) + · · · + rmn (a + b)mn = 0,
o que mostra que a + b satisfaz uma equação polinomial de grau mn com coecientes racionais.
Lema 8 O produto de dois números algébricos é algébrico.
Demonstração.
Segue as mesmas linhas da demonstração anterior. Em (4), entretanto, consideramos as potências
1, ab, (ab)2 , · · · , (ab)mn .
∴ Pelos lemas anteriores os números algébricos formam um corpo.
8
4
Números irracionais
4.1
O número
e
é irracional
O número de Euler e é transcendente, logo e é irracional. Porém, apresentaremos uma demonstação
canônica e de fácil compreensão do fato de e ser irracional, antes de apresentar a prova de que este
número é transcendente.
Teorema 9 O número de Euler, e, é irracional.
Demonstração.
Como já vimos,o número de Euler pode ser calculado através da seqüência:
e=
∞
X
1
1
1
= 1 + + + ···
n!
1! 2!
(5)
n=0
Suponhamos, por absurdo que e seja racional, isto é, e = pq com p, q ∈ Z, q 6= 1 (pois e não é
inteiro). Se assim for, como cada termo da série dada em (5) é racional, temos que o resto da série,
dado por:
q
∞
X
X
1
1
e−
=
,
(6)
n!
n!
n=0
n=q+1
também é racional.
Temos também a seguinte desigualdade para n ≥ q + 1:
1
1
1
1
1
=
≤
,
n!
q! (q + 1) · · · n
q! (q + 1)n−q
que implica:
∞
∞
X
1
1 X
1
11
≤
=
.
k
n!
q!
q! q
(q + 1)
n=q+1
(7)
k=0
A última igualdade decorre da fórmula para a soma de uma série geométrica. De (6) e (7), segue
que:
q
X
11
1
≤
,
0<e−
n!
q! q
n=0
donde
q
X
1
1
0 < q!(e −
) ≤ < 1.
n!
q
n=0
O termo central, pela nossa hipótese é inteiro pois todos os denominadores da expressão entre
parênteses são cancelados pelo q!. Mas isso é um absurdo pois não existe inteiro entre 0 e 1. Assim,
não nos resta alternativa a não ser o fato de que e é irracional.
9
4.2
O número
π
é irracional
A irracionalidade de π foi demostrada pela primeira vez pelo matemático francês Johann Heinrich
Lambert, em 1761. A prova era muito complicada e baseada em uma fração contínua para a função
tan x. Em 1794, Legendre provou um resultado mas forte, que π 2 é irracional.
A demonstração da irracionalidade de π , que daremos a seguir, é devida a I. Niven (1947), o
qual usou um método desenvolvido por Hermite para provar a transcendência do número e.
Antes da prova devemos fazer duas observações:
Primeiro considere a função
xn (1 − x)n
fn (x) =
,
n!
1
onde n é um número inteiro positivo. É claro que 0 < fn (x) < n!
para 0 < x < 1.
Considere, agora, a expressão obtida expandindo o produto xn (1 − x)n , a menor potência de x
que aparece é n e a maior potência é 2n. Logo fn pode ser escrita da forma
2n
1 X i
ci x ,
n!
fn (x) =
i=n
(k)
onde os números ci são inteiros. É claro desta expressão que fn (0) = 0 se k < n ou k > 2n. Mas
ainda,
1
[n!cn + termos envolvendo x]
n!
1
fn(n+1) (x) = [(n + 1)!cn+1 + termos envolvendo x]
n!
..
.
fn(n) (x) =
fn(2n) (x) =
1
[(2n)!c2n ].
n!
Isto signica que
fn(n) (0) = cn ,
fn(n+1) (0) = (n + 1)cn+1 ,
..
.
fn(2n) (0) = (2n)(2n − 1) · . . . · (n + 1)c2n ,
(k)
onde os números da direita são todos inteiros. Logo fn (0) é inteiro para todo k .
(k)
(k)
(k)
A relação fn (x) = fn (1 − x) implica que fn (x) = (−1)k fn (1 − x); Daí fn (1) é também um
inteiro para cada k .
A outra observação é que se a é qualquer número, e ε > 0, então para n sucientemente grande
temos
an
< ε.
n!
Para provar isto, note que se n ≥ 2a, então
an+1
a
an
1 an
=
·
< · .
(n + 1)!
n + 1 n!
2 n!
10
Agora, seja n0 qualquer número natural com n0 ≥ 2a. Então os valores sucessivos satisfazem
1 an0
an0 +1
< ·
(n0 + 1)!
2 (n0 )!
n
+2
0
a
1
an0 +1
1 1 an0
< ·
< · ·
(n0 + 2)!
2 (n0 + 1)!
2 2 (n0 )!
..
.
an0
1
an0 +k
< k·
.
(n0 + k)!
2 (n0 )!
n
n +k
0
Se k é tão grande que (na0 )!ε
< 2k , então (na 00+k)! < ε, que é o resultado desejado.
Tendo feito essas observações, estamos prontos para provar o seguinte teorema:
Teorema 10 O número π é irracional.
Demonstração.
Note que a irracionalidade de π 2 implica a irracionalidade de π , pois se π fosse
racional, então
deveria ser.
Suponha que π 2 é racional, ou seja π 2 = ab para alguns inteiros positivos a e b. Seja
π2
G(x) = bn [π 2n fn (x) − π 2n−2 f´00n (x) + π 2n−4 fn(4) (x) − . . . + (−1)n fn(2n) (x)].
(8)
(k)
Note que cada fator bn π 2n−2k = bn (π 2 )n−k = bn ( ab )n−k = an−k bk é um inteiro. Como fn (0) e
(k)
fn (1) são inteiros, isto mostra que G(0) e G(1) são inteiros.
Derivando G duas vezes obtemos:
n (2n+2)
G00 (x) = bn [π 2n fn00 (x) − π 2n−2 f´(4)
(x)].
n (x) + . . . + (−1) fn
(2n+2)
O último termo, (−1)n fn
(x), é zero. Logo somando (8) e (9) obtemos
G00 (x) + π 2 G(x) = bn π 2n+2 fn (x) = π 2 an fn (x).
Agora seja
(9)
H(x) = G0 (x) sen(πx) − πG(x) cos(πx).
Então
H 0 (x) = πG0 (x) cos(πx) + G00 (x) sen(πx) − πG0 (x) cos(πx) + π 2 G(x) sen(πx)
= [G00 (x) + π 2 G(x)] sen(πx)
= π 2 an fn (x) sen(πx), por (10).
Pelo Teorema Fundamental do Cálculo,
Z 1
π2
an fn (x) sen(πx)dx = H(1) − H(0)
0
= G0 (1) sen π − πG(1) cos π − G0 (0) sen 0 + πG(0) cos 0
= π[G(1) + G(0)].
11
(10)
Por tanto
Z
π
1
an fn (x) sen(πx)dx é um inteiro.
0
n
1
para 0 < x < 1, então 0 < πan fn (x) sen πx < πa
por outro lado, 0 < fn (x) < n!
n! para
R1 n
πan
0 < x < 1. Em conseqüencia, 0 < π 0 a fn (x) sen(πx)dx < n! .
Esse raciocínio foi completamente independente do valor de n. Agora, se n for sucientemente
grande, então
Z 1
πan
< 1,
0<π
an fn (x) sen(πx)dx <
n!
0
pela segunda observação.
Mas isso é absurdo pois a integral é um inteiro e não existe um inteiro entre 0 e 1.
provem de supor que π 2 é racional, logo π 2 é irracional e, por tanto, π é irracional.
O erro
Observação 11 Esta prova é um tanto misteriosa, quiça o mais misterioso de tudo é a forma em
que π entra na prova, pois temos provado que π é irracional sem mencionar a denição de π , mas
usamos uma propriedade de π que é essencial: sen(π) = 0.
4.3
Outros números irracionais
Problemas de irracionalidade são frequentemente difíceis, algumas√vezes intratáveis, e constituem
uma excitante área de pesquisa. A prova da irracionalidade de 2, a diagonal do quadrado de
lado 1, é atribuída a Pitágoras (569-500 a.C.) ou em alguns casos a seus discípulos. Em Theaetetus,
Platão reportou
a prova de seu mestre, Theodorus de Cyrene (450 ac), da irracionalidade
√ √
√
de 3, 5, . . . , 17, obtida usando guras geométricas.
Ainda não se sabe se a constante de Euler-Mascheroni
γ = lim (1 +
n→∞
1
1
+ · · · + − log n)
2
n
é racional ou irracional.
Em 1978, Apéry apresentou uma prova da irracionalidade de ζ(3), onde
∞
X
1
ζ(s) =
=
ns
n=1
Y
p primo
1
(s > 1),
1 − p−s
mas o problema da irracionalidade de ζ(s) para s impar > 3 ainda não foi resolvido.
Também não se sabe se π e e 2e são irracionais. Porem, o matemático russo Alexander Osipovich
Gelfond provou no ano 1929, que eπ é irracional.
Já foi demonstrado que se a > 0 é um inteiro então ea e π a são irracionais e uma conseqüência
p
p
imediata deste fato é que se pq é um número racional no nulo, então e q e π q são irracionais, logo
√
√
5
e2 , e, π 3 , π 3 são irracionais.
12
5
5.1
Números transcendentes
O número
e
é transcendente
A transcendência de e foi um desao aos matemáticos até o século XIX. A prova original da transcendência de e é devida ao matemático francês C. Hermite (1873), a qual sofreu simplicações sucessivas
por matemáticos famosos como Jordan (1882), Markho (1883), Rouché (1883), Weierstrass (1885),
Hilbert (1893), Hurwitz (1893) e Veblen (1904).
A demonstração que apresentamos a seguir é uma variação, devida a Hurwitz, da prova de
Hilbert.
Teorema 12 O número e é transcendente.
Demonstração.
Suponha que e é algébrico. Logo am em + · · · + a1 e + a0 = 0, para certos ai ∈ Q,
i = 0, ..., m e a0 6= 0. Podemos supor, sem perda da geralidade, que os ai são inteiros para todo i.
p−1
p (x−2)p ...(x−m)p
O polinômio f (x) = x (x−1) (p−1)!
, onde p é um número primo, é de grau mp + p − 1,
o que implica que f (mp+p) (x) = 0.
Seja F (x) = f (x) + f 0 (x) + · · · + f (mp+p−1) (x). Temos
d −x
{e F (x)} = e−x {F 0 (x) − F (x)} = −e−x f (x)
dx
(11)
logo, para todo j ,
Z
aj
0
j
e−x f (x)dx = aj [−e−x F (x)]j0 = aj F (0) − aj e−j F (j).
Multiplicando ambos lados por ej e somando para j = 0, 1, ..., m, obtemos
m X
aj e
j=0
j
Z
j
−x
e
m
m
X
X
f (x)dx = F (0)
aj ej −
aj F (j)
0
j=0
=−
m mp+p−1
X
X
j=0
(12a)
j=0
aj f (i) (j).
i=0
Lema 13 Para todo i e j , f (i) (j) é um inteiro divisível por p exceto se j = 0 e i = p − 1, e então
f (p−1) (0) = (−1)p ...(−m)p .
Segue-se que a expressão (12a) é da forma Kp − a0 (−1)p ...(−m)p , com K ∈ Z.
Se p > sup(m, |a0 |), o inteiro a0 (−1)p ...(−m)p não é divisível por p. Logo para um número
primo p sucientemente grande, o lado esquerdo de (12a) é um inteiro que não é divisível por p e
por tanto Kp − a0 (−1)p ...(−m)p é não nulo.
Vamos dar uma cota superior para a integral. Se 0 ≤ x ≤ m, então
|f (x)| ≤
mmp+p−1
,
(p − 1)!
13
o que implica que
X
X
Z j
Z j mp+p−1
m
m
m
−x
j
(aj ej
dx
e f (x)dx) ≤
|aj | e
0
0 (p − 1)!
j=0
j=0


m
X
mmp+p
≤
|aj | ej 
,
(p − 1)!
j=0
que tende a 0 quando p tende a innito.
Logo obtivemos uma contradição, o qual prova que e é transcendente.
Demonstração do Lema. Usando a regra de Leibniz, se j 6= 0, então o único termo não nulo vem
p!
do fator (x − j)p derivando p vezes. Desde que (p−1)!
= p, esse termos são inteiros divisíveis por p.
Se j = 0, o único termo não divisível por p é obtido para i = p − 1 e então
f (p−1) (0) = (−1)p ...(−m)p .
5.2
O número
π
é transcendente
Lindemann, em 1882, extendeu a demonstração de que e é transcendente e mostrou que π é transcendente.
5.2.1 Polinômios simétricos
Mas, antes de apresentar a demonstração de que π é transcendente, necessitamos enunciar alguns
fatos a respeito de polinômios simétricos.
Denição 14 Um polinômio p(x1 , . . . , xn ) é dito
tação σ : {1, . . . , n} → {1, . . . , n} vale:
simétrico se, e somente se, para qualquer permu-
pσ (x1 , . . . , xn ) := p(xσ(1) , . . . , xσ(n) ) = p(x1 , . . . , xn ).
Denição 15 Dado um monômio
axk11 . . . xknn , seu peso é o número
polinômio é o máximo entre os pesos de seus monômios.
Denição 16 Os polinômios simétricos dados por:
s1 =
n
X
xj ,
j=1
s2 =
X
xi xj ,
1≤i<j≤n
..
.
sn = x1 . . . xn ,
são chamados os polinômios simétricos elementares.
14
j=1 jkj .
Pn
O peso de um
Os teoremas a seguir são provados para um corpo K qualquer, e para os polinômios com coecientes em K (isto é, polinômios em K[x]), embora só precisemos deles no caso em que K = Q.
Claramente, um polinômio nas variáveis s1 , . . . , sn denidas acima são polinômios simétricos nas
variáveis x1 , . . . , xn . O teorema a seguir é a recíproca.
Teorema 17 Dado p(x1 , . . . , xn ) ∈ K[x1 , . . . , xn ] simétrico de grau d, existe q(s1 , . . . , sn ) ∈ K[s1 , . . . , sn ]
de peso menor ou igual a d, tal que
p(x1 , . . . , xn ) = q(s1 , . . . , sn ),
onde si são denidos na denição 16.
Demonstração.
Se n = 1, o teorema é óbvio. Agora, suponhamos o teorema verdadeiro para
n − 1. Para provar que o teorema vale para n, procedemos por indução em d.
Se d = 0, não há o que provar, pois p(x1 , . . . , xn ) é constante. Agora supomos o teorema válido
se o grau é menor que d.
Sejam s1 , . . . , sn−1 os polinômios elementares em x1 , . . . , xn−1 . Pela hipótese de indução existe
q1 (s1 , . . . , sn−1 ) de peso ≤ d − 1 tal que:
p(x1 , . . . , xn−1 , 0) = q1 (s1 , . . . , sn−1 ).
Denindo p1 = p − q1 , obtemos um polinômio simétrico em x1 , . . . , xn , pois p, q1 também são
simétricos. Fazendo xn = 0, pela equação acima:
p1 (x1 , . . . , xn−1 , 0) = p(x1 , . . . , xn−1 , 0) − q1 (s1 , . . . , sn−1 ) = 0.
(13)
O que implica que xn é fator comum de p1 . Mas como este é simétrico, então cada xj é fator
comum de p1 e, portanto, sn é fator comum. Resumindo:
p1 (x1 , . . . , xn ) = sn p2 (x1 , . . . , xn ).
(14)
O grau de p2 é ≤ d − n. Aplicando a indução, obtemos q2 (s1 , . . . , sn ) de peso ≤ d − n que
coincide com p2 (x1 , . . . , xn ). Usando este fato e substituindo em (14) e, depois, em (13), chegamos
à igualdade:
p(x1 , . . . , xn ) = sn q2 (s1 , . . . , sn ) + q1 (s1 , . . . , sn ) = q(s1 , . . . , sn ),
que tem grau ≤ d.
Esse teorema mostra que o conjunto dos polinômios simétricos em K[x] é um subanel.
Teorema 18 Sejam α1 , . . . , αn números algébricos, tais que os polinômios simétricos elementares
s1 =
n
X
αj ,
j=1
s2 =
X
αi αj ,
1≤i<j≤n
..
.
sn = α1 . . . αn ,
estão em K . Considere os nk elementos algebricos βi1 ,...,ik = αi1 + · · · + αik . Então os polinômios
simétricos elementares associados aos βi1 ,...,ik também estão em K .
15
Demonstração.
Por simplicidade, provaremos o teorema para k = 2, mas a demonstração no
caso geral é idêntica. Para isso, provaremos que os polinômios simétricos elementares nos βij são
simétricos nos αi .
Seja dada uma permutação σ . Vamos usar a notação σ(p) = pσ . Assim, a ação de σ é, pela
denição:
σ(Σai1 ,...,in α1i1 . . . αnin ) = Σai1 ,...,in σ(α1 )i1 . . . σ(αn )in .
Considere a permutação induzida por σ nos βij , σ̂ , ou seja:
σ̂(βij ) = σ(αi ) + σ(αj ) = σ(βij ).
Temos, portanto, que, para cada permutação elementar Sk dos βij :
σ(Sk ) = σ̂(Sk ) = Sk ,
uma vez que os Sk são simétricos em βij . Isso mostra que eles também são simétricos nos αi , e,
aplicando o teorema 17, obtemos o resultado desejado.
Corolário 19 Sejam os αi´s do teorema anterior, as raízes de um polinômio P (x) ∈ K[x] de grau
n. Então
os
n
grau
k
.
n
k
números βi1 ,...,ik = αi1 + · · · + αik são as raízes de um polinômio em K[x] que tem
Demonstração.
Basta observar que P (x) = xn − s1 xn−1 + s2 xn−2 + · · · + (−1)n sn , onde si são os
polinômios simétricos elementares em α1 , . . . , αn . Logo temos si ∈ K , e aplicamos o teorema.
5.2.2 Demonstração
A demonstração a seguir é baseada na prova de Hurwitz para transcendência de e, que é aquela
dada na seção 5.1.
Teorema 20 O número π é transcendente.
Demonstração.
Suponhamos, por absurdo, que π seja algébrico. Assim, iπ , produtos de dois
algébricos, seria também algébrico. Então iπ é raiz de um polinômio com coecientes inteiros.
Sejam α1 = iπ, α2 , . . . , αn as raízes deste polinômio.
Da conhecida igualdade de Euler eiπ + 1 = 0, segue-se:
0=
n
Y
αj
(1 + e ) = k +
j=1
m
X
eβj ,
(15)
j=1
onde k ∈ N e β1 , β2 , · · · , βm são os números não-nulos dentre:
αi ,
αi + αj ,
1≤i≤n
(16)
1≤i<j≤n
(17)
..
.
α1 + · · · + αn ,
16
(18)
e k ∈ N é obtido agrupando a soma dos termos cujos expoentes são nulos.
Os números β1 , β2 , · · · , βm dados anteriormente são as raízes de um polinômio R(x) = cxm +
cm−1 xm−1 + · · · + c1 x + c0 de coecientes inteiros devido ao corolário 19. Tomando um primo p
genérico e s = m(p − 1), denamos:
f (x) =
cs
xp−1 (R(x))p .
(p − 1)!
(19)
O grau de P é s + p. Denamos também:
F (x) = f (x) + f 0 (x) + · · · + f (s+p) (x),
que, assim como em (11), satisfaz:
d −x
e F (x) = −e−x f (x),
dx
donde:
−x
e
x
Z
F (x) − F (0) = −
e−t f (t)dt.
0
Assim, usando a mudança de variável t = λx (onde λ é variável e x é xo):
1
Z
x
F (x) − e F (0) = −x
e(1−λ)x f (λx)dλ.
0
Somando as igualdades para x = β1 , . . . , βm , obtemos:
m
X
F (βj ) + kF (0) = −
j=1
m
X
Z
βj
j=1
1
e(1−λ)βj f (λβj )dλ.
(20)
0
Notando em (19) que βj é raiz de f (x) de multiplicidade p, chegamos à conclusão que:
0≤t<p⇒
m
X
f (t) (βj ) = 0.
j=1
Se t ≥ p, apenas a p-ésima derivada de R(x) no ponto x = βj é não-nula. Derivando p vezes
o polinômio R(x) neste ponto, teremos um coeciente p! que cancelará o denominador (p − 1)! de
f (x), deixando p vezes um polinômio com coecientes inteiros calculado em βj . TudoPisso implica
(t)
que c1s f t (βj ) é polinômio em βj com coecientes inteiros divisíveis por p. Além disso, m
j=1 f (βj )
s
é simétrico nos βj de grau ≤ s. Logo, devido ao coeciente c , este polinômio é de coecientes
inteiros e grau ≤ s. Assim:
p≤t⇒
m
X
(βj ) = pkt ,
j=1
kt inteiros.
Agora examinamos F (0). Notamos que f (t) (0) = 0 se t ≤ p − 2, f (p−1) (0) = cs cp0 e f (t) (0) é
inteiro divisível por p se p ≤ t.
Portanto, o termo em (20) é da forma Kp + kcs cp0 com K inteiro; tal expressão é um inteiro.
Tomando p > max{k, |c|, |c0 |}, conseguimos em (20) um termo não divisível por p (pois kcs cp0 não
pode ser divisível), e, logo, não nulo. De (19), obtemos:
17
|f (λβj )| ≤
|c|s mpj
(p − 1)!
|βj |p−1
que segue se tomarmos mj = max0≤λ≤1 |R(λβj )|. Portanto
|−
m
X
j=1
Z
1
(1−λ)βj
e
βj
f (λβj )dλ| ≤
0
m
X
|βj |p |c|s |mj |p B
j=1
(p − 1)!
,
(21)
R1
onde B = supj 0 |e(1−λ)βj |dλ.
O lado esquerdo da equação (21) é não nulo e o lado direito tende a zero quando p → ∞, o que
é um absurdo. Logo, π é transcendente.
5.3
Outros números transcendentes
Trabalhando independentemente, A. O. Gelfond em 1934 e T. Schneider em 1935 resolveram o 7o
problema apresentado por Hilbert no Congresso Internacional de Matemática em 1900, provando o
seguinte resultado:
e α e β são números complexos algébricos, com α 6= 0, 1 e se β é irracional então αβ é um número
transcendente.
√
√ √2
Este resultado arma, por exemplo, que os números 2 2 (constante de Gelfond-Schneider), 2 ,
eπ = (eiπ )−i = (−1)i (constante de Gelfond) são transcendentes.
Entre tanto, o caso de β irracional transcendente ainda não foi resolvido, em particular não se
sabe se π e é transcendente.
Outros números transcendentes são:
1. sen(a), cos(a), tan(a) para qualquer número algébrico não nulo a.
2. ln(a) se a é positivo, racional e diferente de 1.
3. 0, 12345678910111213141516... a constante de Champernowne.
Números que ainda não se sabe se são transcendentes ou não:
1. Somas, produtos, potências, etc (exceto a constante de Gelfond) do número π e o número e:
π + e, π − e, π e , πe , π π , ee , πe.
2. A constante de Euler-Mascheroni, γ .
3. A constante de Apéry, ζ(3).
18
Referências
[BB] BORWEIN, J.M., BORWEIN, P.B.; Pi and the AGM. Canadian Mathematical Society.
[EL] EYMARD, P., LAFON J.P.; The Number π, A.M.S 2004
[FI] FIGUEIREDO, D. G. ; Números Irracionais e Transcendentes, S.B.M. 2002
[HE] HERSTEIN, I.N.; Topics in Algebra, John Wiley and Sons 1975
[SP] SPIVAK, M.; Calculus, W. A. Benjamin 1967
19