a) Condição de primeira ordem de maximização do lucro em

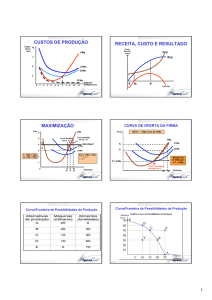
Exercício 16 – Microeconomia II – LGE108
1
a) Condição de primeira ordem de maximização do lucro em concorrência perfeita:
p = Cmg
CT = 0, 5q 3 − 10q 2 + 100q + 784
dCT
Cmg =
= 1.5q 2 − 20q + 100 ⇔ p = 1.5q 2 − 20q + 100 ⇔
dq
(6 p − 200 )
20
±
3
3
Condição de segunda ordem de maximização do lucro em concorrência perfeita:
dCmg
20
≥ 0 ⇔ 3q − 20 ≥ 0 ⇔ q ≥
dq
3
⇔ 1.5q 2 − 20q + (100 − p ) = 0 ⇔ q =
Logo:
(6 p − 200)
20
+
3
3
O empresário, no curto prazo, só produz se p ≥ min CVM
q=
CVT = 0,5q 3 − 10q 2 + 100q
CVT
CVM =
= 0,5q 2 − 10q + 100
q
Condição de primeira ordem de minimização do CVM :
dCVM
= 0 ⇔ q − 10 = 0 ⇔ q = 10
dq
CVM
= 0,5 ⋅ (10 ) − 10 ⋅ (10 ) + 100 = 50
2
q =10
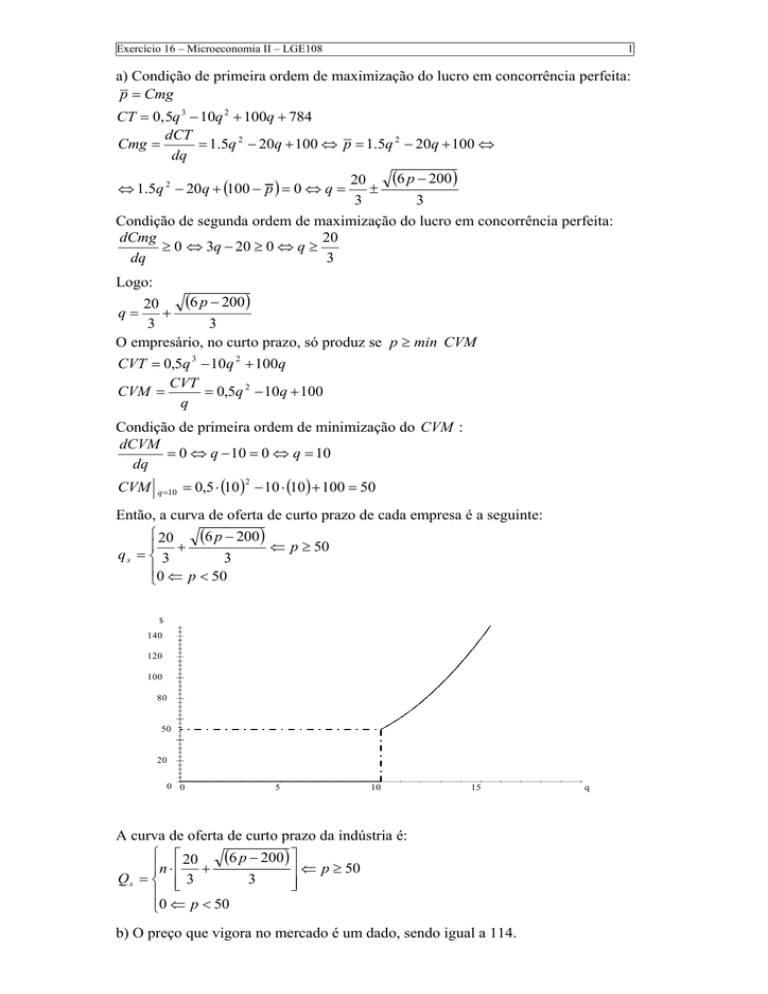
Então, a curva de oferta de curto prazo de cada empresa é a seguinte:
⎧ 20
(6 p − 200 )
⎪ +
⇐ p ≥ 50
qs = ⎨ 3
3
⎪0 ⇐ p < 50
⎩
$
140
120
100
80
50
20
0 0
5
10
15
A curva de oferta de curto prazo da indústria é:
⎧ ⎡ 20
(6 p − 200 ) ⎤
⎪n ⋅ ⎢ +
⎥ ⇐ p ≥ 50
Q s = ⎨ ⎣⎢ 3
3
⎦⎥
⎪
⎩0 ⇐ p < 50
b) O preço que vigora no mercado é um dado, sendo igual a 114.
q
Exercício 16 – Microeconomia II – LGE108
2
Em equilíbrio,
Qs = Qd
P = 114 ⇒ Q D = 612000 − 5000 ⋅ (114 ) = 42000
⎧ 20
(6(114) − 200)
⎪ +
⇔ q s = 14
qs = ⎨ 3
3
⎪0 ⇐ p < 50
⎩
Qs = Qd
n ⋅ q s = 42000 ⇔ 14n = 42000 ⇔ n = 3000
$
Cmg
CTM
140
114
CVM
50
0 0
5
14
10
q
$
Qs
140
Qd
114
80
60
40
20
0 0
10000
20000
Q
30000
42000
Q
c) Apesar da empresa estar a auferir lucros normais, essa é uma condição necessária,
mas não suficiente para a existência de equilíbrio de longo prazo. É preciso que a
empresa esteja a laborar na dimensão óptima mínima (condição necessária e
suficiente).
d.1)Vamos tentar exprimir a função oferta não em termos de preço que o produtor
recebe, mas em termos de preço que o consumidor paga.
CT ' = CT + 4.2q
CVT ' = CVT + 4.2q
CVM ' = CVM + 4.2
Cmg ' = Cmg + 4.2
Condição de primeira ordem de maximização do lucro em concorrência perfeita:
p = Cmg '
Exercício 16 – Microeconomia II – LGE108
3
p = 1.5q 2 − 20q + 104.2 ⇔
(6 p − 225.2 )
20
±
3
3
Condição de segunda ordem de maximização do lucro em concorrência perfeita:
dCmg '
20
≥ 0 ⇔ 3q − 20 ≥ 0 ⇔ q ≥
3
dq
⇔ 1.5q 2 − 20q + (104.2 − p ) = 0 ⇔ q =
Logo:
(6 p − 225.2)
20
+
3
3
O empresário, no curto prazo, só produz se p ≥ min CVM '
dCVM '
= 0 ⇔ q = 10
dq
q=
CVM '
= 0,5 ⋅ (10 ) − 10 ⋅ (10 ) + 104.2 = 54.2
2
q =10
A curva de oferta de curto prazo de cada empresa é a seguinte:
⎧ 20
(6 p − 225.2)
⎪ +
⇐ p ≥ 54.2
qs ' = ⎨ 3
3
⎪0 ⇐ p < 54.2
⎩
d.2)
No curto prazo, o imposto é repartido entre consumidores e vendedores, dependendo
essa repartição do valor da elasticidade-preço da procura e da oferta no ponto de
equilíbrio antes do lançamento do imposto. O preço de mercado (pago pelos
consumidores) pertence ao intervalo [114; 118,2], correspondendo o limite inferior ao
caso em que a elasticidade-preço da procura é perfeitamente elástica e o superior ao
caso em que é perfeitamente inelástica.
Se a curva da procura fosse perfeitamente inelástica:
$
118.2
114
54.2
50
0
30000
42000
Q
Exercício 16 – Microeconomia II – LGE108
4
Se a curva da procura fosse perfeitamente elástica:
$
114
54.2
50
0
30000
41435 42000
Q
Então, o preço pago pelo consumidor estará entre 114 (curva da procura perfeitamente
elástica) e 118,2 (curva da procura perfeitamente inelástica).
O caso presente não corresponde a nenhum destes casos limite, pelo que o preço de
mercado irá situar-se no interior desse intervalo: mais próximo do limite inferior se,
na situação de equilíbrio inicial, a elasticidade-preço da procura for maior do que a
elasticidade-preço da oferta ou mais próximo do limite superior, no caso inverso.
d.3) Como a função oferta, no período longo, é perfeitamente elástica, o preço pago
pelo consumidor aumentará em 4.2, passando a ser de 118.2.
$
P=118.2
P=114
Qd
0
21000
42000
Q