Questão Alternativa 1 E 2 B 3 E 4 A 5 C 6 B 7 E 8 A 9 E 10 C 11 D

Questão
1 de 1
http://itamaraty.ime.usp.br/mat/2457/Gabaritos/GPRec - 2010.html
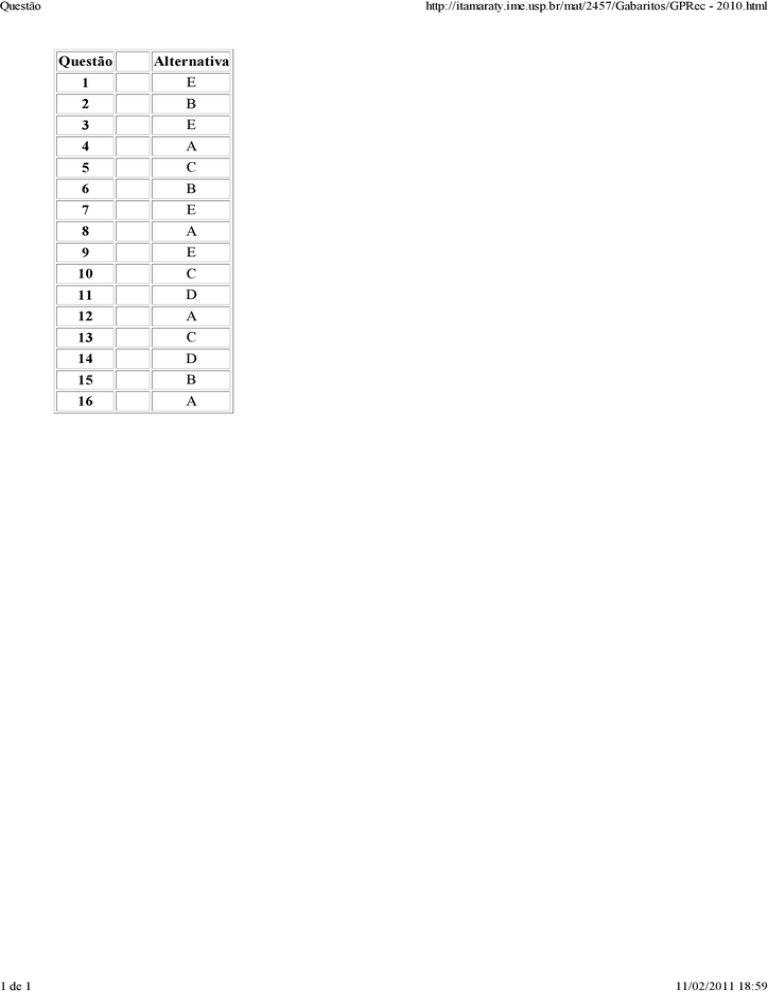
Questão
1
Alternativa
E
4
5
A
C
8
9
A
E
12
13
A
C
16
B
A
2
3
6
7
B
E
B
E
10
11
C
D
14
15
D
11/02/2011 18:59
Q1. Seja λ ∈ R e considere os vetores:
v1 = (1, 1, λ, 1),
v2 = (1, 1, λ, 2),
v3 = (1, 1, λ, 0),
v4 = (0, 0, 1, λ)
no espaço vetorial R4 . Pode-se afirmar que:
(a)
(b)
(c)
(d)
(e)
{v1 , v2 , v3 , v4 } é uma base de R4 ;
v4 ∈ [v1 , v2 , v3 ];
[v1 , v2 ] = [v3 , v4 ];
a dimensão de [v1 , v2 , v3 ] é igual a 3;
{v1 , v2 , v4 } é uma base de [v1 , v2 , v3 , v4 ].
Q2. Sejam B = {~e1 , ~e2 , ~e3 } e C = {f~1 , f~2 , f~3 } bases de V 3 tais que a matriz
de mudança de base MBC é:


1 0 1
MBC = 0 1 1  .
1 0 −1
Seja ~v ∈ V 3 um vetor cujas coordenadas na base B sejam [~v ]B = (4, 2, 6).
As coordenadas de ~v na base C são:
(a)
(b)
(c)
(d)
(e)
[~v ]C
[~v ]C
[~v ]C
[~v ]C
[~v ]C
= (8, 4, 12);
= (5, 3, −1);
= (10, 8, −2);
= (10, 6, −2);
= (4, 2, 6).
Q3. A solução da equação diferencial y 000 − 3y 00 + 3y 0 − y = 0 satisfazendo
as condições iniciais y(0) = 1, y 0 (0) = 0 e y 00 (0) = −1 é:
(a) y(t) = et + tet +
(b)
(c)
(d)
(e)
t2 t
2e ;
y(t) = et − t2 et ;
y(t) = et ;
y(t) = et + tet + t2 et ;
y(t) = et − tet .
Q4. Considere fixado um sistema de coordenadas Σ = (O, E) em E 3 , sendo
E uma base ortonormal de V 3 . Considere os planos:
π1 : 2x − y + 2z + 6 = 0,
π2 : 6x − 3y + 6z + 9 = 0.
A distância entre π1 e π2 é igual a:
(a)
(b)
(c)
(d)
(e)
1;
0;
4;
2;
3.
Q5. Considere fixado um sistema de coordenadas Σ = (O, E) em E 3 , sendo
E uma base ortonormal de V 3 . Considere as retas:
r : X = (1, 2, −1) + λ(3, 4, 0), λ ∈ R,
s : X = (0, 1, −2) + λ(3, 4, 5), λ ∈ R.
Assinale a alternativa correta:
(a)
(b)
(c)
(d)
(e)
o vetor (−4, 3, 1) é normal às retas r e s;
as retas r e s são coincidentes;
as retas r e s são reversas;
as retas r e s estão contidas num mesmo plano;
as retas r e s são concorrentes.
Q6. Considere fixado um sistema de coordenadas Σ = (O, E) em E 3 , sendo
E uma base ortonormal de V 3 . Considere os pontos:
A = (0, 0, 0),
B = (1, 1, 0),
C = (0, 1, 1),
O volume do tetraedro ABCD é igual a:
(a) 2;
(b) 31 ;
(c) 1;
(d) 23 ;
(e)
2
3.
D = (1, 0, 1).
Q7. Considere o subespaço de R4 definido por:
S = (x + 2y, x + 2y + z, x + 2y − z, 2x + 4y − z) : x, y, z ∈ R .
Assinale a alternativa em que B é uma base para S:
(a)
(b)
(c)
(d)
(e)
B
B
B
B
B
= {(1, 0, −1, 1), (2, 0, −1, 1)};
= {(0, 1, −2, 1), (1, 1, 0, 1)};
= {(1, 0, 1, 0), (1, 1, −2, 1)};
= {(2, 1, 3, −1), (2, −1, 3, 1)};
= {(2, −1, 5, 7), (2, 5, −1, 1)}.
Q8. Considere o subespaço:
S = [(1, 1, 2, 2), (2, 3, 5, 5), (0, 1, 1, 1), (1, 1, 3, 1)]
R4 .
de
Assinale a alternativa em que a união de uma base de S com o
conjunto B resulta em uma base de R4 :
(a)
(b)
(c)
(d)
(e)
B
B
B
B
B
= {(−1, 1, 0, −2)};
= {(4, 2, 6, 6)};
= {(3, 3, 6, 6)};
= {(3, 3, 7, 5)};
= {(1, 2, 1, 5)}.
Q9. Seja k ∈ R e considere o sistema linear:


 x + y − z = 1,
x − y − z = 1,

 3x − y − kz = 0.
Pode-se afirmar que:
(a)
(b)
(c)
(d)
(e)
o sistema possui infinitas soluções se e somente se k = 2;
existe um único k ∈ R tal que o sistema possui uma única solução;
existe um único k ∈ R tal que o sistema possui infinitas soluções;
o sistema possui uma única solução se e somente se k = 4;
o sistema não possui solução se e somente se k = 3.
Q10. Seja fixado um sistema de coordenadas em E 3 . Considere o vetor
~v = (1, 1, 1), a reta:
r : X = (1, 0, 1) + t(2, −1, 1), t ∈ R,
e o plano π : x − y + 2z + 1 = 0. Se ~v = p~ + ~q com p~ ∈ V 3 paralelo à reta r
e ~q ∈ V 3 paralelo ao plano π, pode-se afirmar que:
(a) ~q = 51 (9, 3, −3);
(b) ~q = 51 (−7, −1, 3);
(c) ~q = 51 (1, 7, 3);
(d) ~q = 51 (3, 1, −1);
(e) ~q = 51 (−5, −1, 2).
Q11. Considere fixado um sistema de coordenadas Σ = (O, E) em E 3 , sendo
E uma base ortonormal de V 3 . Uma equação geral para o plano π que contém
o ponto (1, −1, 2) e é perpendicular à reta:
x − 2y + z − 1 = 0,
r:
x + y − z + 2 = 0,
é:
(a)
(b)
(c)
(d)
(e)
x − 2y + 3z − 9 = 0;
x + 2y − z + 3 = 0;
2x + 3y + z − 1 = 0;
2x + 4y + 6z − 10 = 0;
2x + 2y + z − 2 = 0.
Q12. Seja fixado um sistema de coordenadas em E 3 . Seja b ∈ R e considere
as retas:
x − y + 2z = 1,
r : X = (b, 0, 1) + λ(1, b, −b), λ ∈ R, s :
y + 2z = b.
Pode-se afirmar que:
(a)
(b)
(c)
(d)
(e)
se
se
se
se
se
b=1
b = 12
b=1
b = 12
b=1
então as retas r e s são concorrentes;
então as retas r e s são reversas;
então as retas r e s são paralelas distintas;
então as retas r e s são paralelas distintas;
então as retas r e s são coincidentes.
−−→ −−→
Q13. Sejam A, B, C, D, P, Q ∈ E 3 . Sabe-se que os vetores AB e AD determinam um quadrado de lado unitário. Sabe-se também que:
−−→
−−→
−−→ −−→
4BP = 3BC, 3DQ = DC.
−→
Pode-se afirmar que a área do paralelogramo determinado pelos vetores AP
−−→
e BQ é igual a:
(a)
(b)
(c)
(d)
(e)
3
5;
1
3;
3
2;
4
5;
3
4.
Q14. Considere fixado um sistema de coordenadas Σ = (O, E) em E 3 , sendo
E uma base ortonormal de V 3 . A reta r contém o ponto P = (1, 2, 1) e é
paralela ao vetor ~v = (1, −1, 1). O plano π contém o ponto Q = (−1, 1, 1) e
é perpendicular ao vetor w
~ = (1, 1, −1). Pode-se afirmar que:
(a)
(b)
(c)
(d)
(e)
r
r
r
r
o
e π são perpendiculares;
está contida em π;
é paralela a π e r não está contida em π;
e π possuem um único ponto em comum;
ponto P pertence ao plano π.
Q15. Sejam α, β ∈ R e considere os vetores:
v1 = (1, −1, 0, 1),
v2 = (−2, 1, 3, 1),
v3 = (2, 1, α, 5),
v4 = (α, 0, β, 0)
no espaço vetorial R4 . Se S = [v1 , v2 , v3 , v4 ], pode-se afirmar que:
(a)
(b)
(c)
(d)
(e)
dim(S) = 3 se e somente se α + 3β = 0;
dim(S) = 4 se e somente se α2 − 9α − 6β 6= 0;
dim(S) = 3 se e somente se α = −9 e β = 27;
dim(S) = 3, para quaisquer α, β ∈ R;
existem α, β ∈ R tais que dim(S) = 2.
Q16. Considere os sistemas de coordenadas:
Σ1 = O1 , {~ı, ~, ~k} , Σ2 = O2 , {~e1 , ~e2 , ~e3 } ,
em E 3 . Assuma que:
~e1 = ~ı − ~ + ~k,
~e2 = −~ı + ~ + ~k,
~e3 = ~ı + ~ − ~k,
e que as coordenadas do ponto O2 no sistema Σ1 sejam O2 = (2, 3, 2)Σ1 . A
equação geral de um plano π no sistema Σ2 é x + y + z + 1 = 0. A equação
geral do plano π no sistema Σ1 é:
(a)
(b)
(c)
(d)
(e)
x + y + z − 6 = 0;
x + y + z = 0;
11x − y − z + 6 = 0;
x + y + z + 1 = 0;
2x + 3y + 2z + 1 = 0.