Inteligência Artificial
Alameda e Taguspark
Primeiro Teste
31 de Outubro de 2008
19H00-20H30
Nome:_________________________________________Número:_________
Este teste tem 7 perguntas e 7 páginas. Escreva o número em todas as páginas. Deve ter na mesa apenas
o enunciado do teste, canetas ou lápis e a sua identificação. Pode utilizar o verso das folhas como
rascunho.
As respostas das perguntas de escolha múltipla que contam para avaliação são apenas as identificadas
nesta página. Para estas perguntas é dada uma cotação negativa no caso de a resposta estar errada: se
existirem n alternativas e a cotação for c, então respostas erradas contribuem negativamente para a
classificação final com –c/(n-1).
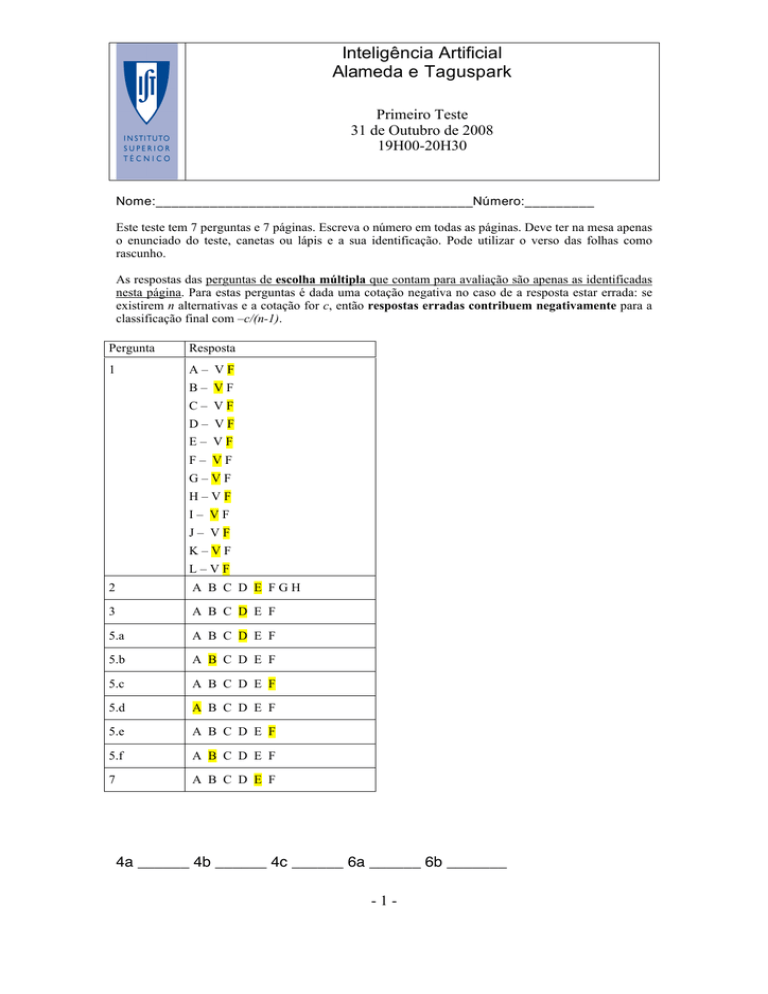
Pergunta
Resposta
1
A– VF
B– VF
C– VF
D– VF
E– VF
F– VF
G–VF
H–VF
I– VF
J– VF
K–VF
L–VF
2
A B C D E FGH
3
A B C D E F
5.a
A B C D E F
5.b
A B C D E F
5.c
A B C D E F
5.d
A B C D E F
5.e
A B C D E F
5.f
A B C D E F
7
A B C D E F
4a ______ 4b ______ 4c ______ 6a ______ 6b _______
-1-
1.
(4.8) Indique se as seguintes frases são verdadeira (V) ou falsas (F):
A) Num ambiente estático os sensores do agente dão acesso ao estado completo do ambiente em cada instante
do tempo _____ F
B) Um agente baseado em utilidade utiliza uma função de utilidade que permite estabelecer preferências entre
sequências de estados que permitem atingir os mesmos objectivos ______ V
C) Na estratégia de procura RBFS (Melhor Primeiro Recursiva), para cada nó explorado, mantém-se registo do
caminho alternativo com o maior valor retornado pela função de avaliação _____ F
D) A estratégia de profundidade limitada é óptima ______ F
E) A procura gananciosa é completa _____ F
F) A* com procura em grafo não é necessariamente óptima com uma heurística admissível ______ V
G) O Hill-Climbing (Trepa Colinas) pode ser visto como um simples ciclo que se move continuamente na
direcção de um valor melhor e que termina quando nenhum sucessor tem valores melhores ______ V
H) O Stochastic Hill Climbing (Trepa Colinas Estocástico) conduz uma séria de procuras a partir de
diferentes estados iniciais ______ F
I) Em cada iteração do Local Beam (Procura em Banda) todos os sucessores dos k estados são gerados
______ V
J) Nos algoritmos genéticos, o estado sucessor é gerado através da combinação de dois estados (pais), sendo
a nova geração produzida unicamente com base em duas operações: selecção e cruzamento ______ F
K) Em jogos, a função de utilidade atribui um valor numérico aos estados terminais ______ V
L) O Minimax pode não ser óptimo, mesmo se o jogo decorrer contra um adversário óptimo ______ F
2.
(1.0) Considere um ambiente Common-Lisp em que foram dadas as seguintes instruções:
> (defun R (x y z)
(if (null z) ()
(if (eq x (car z))
(cons y (R x y (cdr z)))
(cons (car z) (R x y (cdr z))))))
> (defun Y (y) #'(lambda (x) (R (car y) x y)))
> (setf f (Y '(A B A)))
Qual os resultados obtidos ao avaliar as expressões (funcall f 'B) seguida de (funcall f 'C)?
A) () e ()
B) (() B A) e (() B A)
C) (() B ()) e (() B ())
D) (B () B) e (C () C))
E) (B B B) e (C B C)
F) (B B B) e (C C C)
G) (B B A) e (C B A)
H) Erro
-2-
3.
(1.0) Considere agora o seguinte código em Lisp
(defun xpto (l1 l2)
(if (null l1) l2 (cons (first l1) (xpto (rest l1) l2))))
Qual o resultado de avaliar (xpto ‘(5 3) ‘(4 2 6))?
A) (3 5 2 4 6)
B) (6 2 4 3 5)
C) (2 3 4 5 6)
D) (5 3 4 2 6)
E) (3 5 6 4 2)
F) (4 5 2 3 6)
4.
(3.0) A Fofoca é uma foca que trabalha num circo. A tarefa da Fofoca é responder a diferentes
indicações do seu treinador. Assim:
− sempre que apanha 4 peixes (recebidos um de cada vez e não necessariamente consecutivos),
a Fofoca bate palmas (acção PALMAS);
− sempre que apanha uma bola, a Fofoca deve equilibrá-la no focinho (acção EQUILIBRA);
− sempre que o treinador lhe toca na cabeça, a Fofoca deve fazer o pino (acção PINO).
Assuma ainda que:
− Quando o treinador não lhe dá nenhuma indicação, a Fofoca faz “AOHAOH”;
− Faz igualmente “AOHAOH” quando recebe mais do que uma indicação do treinador ao
mesmo tempo (por exemplo, recebe uma bola e faz o pino). Nestes casos fica confusa e faz
apenas “AOHAOH”;
− Apenas de 4 em 4 peixes é que a Fofoca bate palmas, manifestando-se com o “AOHAOH”,
enquanto não chegar ao 4º elemento de cada grupo de peixes (por exemplo, recebe o segundo
peixe e faz “AOHAOH”).
Considere agora que vários circos virtuais encomendaram agentes focas com a mesma
funcionalidade da Fofoca.
a.
(0.5) Defina o tipo percepcao para este agente.
(defstruct percepcao peixe bola cab)
b.
(2.0) Implemente o agente-foca em Lisp.
(defun cria-fofoca ()
(let ((num-px 0))
#'(lambda (p)
(cond ((or (and (percepcao-peixe p)(percepcao-toque p))
(and (percepcao-peixe p)(percepcao-bola p))
(and (percepcao-toque p)(percepcao-bola p))) 'AOHAOH)
((percepcao-bola p) 'EQUILIBRA)
((percepcao-toque p) 'PINO)
((percepcao-peixe p) (if (= num-peixes 3)
(progn (setf num-peixes 0) 'PALMAS)
(progn (incf num-peixes) 'AOHAOH)))
(t 'AOHAOH)))))
c.
(0.5) Que tipo de agente deve ser o agente-foca? Justifique.
É um agente de reflexos com estado interno, dado que necessita de manter informações obre o estado
(nomeadamente sobre o número de peixes apanhado) de modo a poder tomar decisões.
-3-
5.
(6.0) Considere o seguinte espaço de estados com os estados de A a G, representado na figura a
seguir:
Os estados são representados por um círculo com o seu nome e um número, que corresponde à função
de avaliação heurística do estado. Os números nos arcos que ligam dois estados representam os custos
de transição entre os dois estados. O problema que estamos a considerar tem como estado inicial o
estado A e como estados objectivo os estados E e G. Considere que os sucessores de um nó são
gerados pela ordem alfabética dos estados (por exemplo, o primeiro sucessor de A é o nó B e não o nó
C) e que em caso de empate na ordem de colocação de nós na fila de nós por tratar vigora a ordem
alfabética.
a.
(1.0) Considere a procura em largura primeiro e escolha a única opção correcta:
A) São feitos 2 testes a nós para verificar se são soluções do problema.
B) São feitos 3 testes a nós para verificar se são soluções do problema.
C) São feitos 4 testes a nós para verificar se são soluções do problema.
D) São feitos 5 testes a nós para verificar se são soluções do problema.
E) São feitos 6 testes a nós para verificar se são soluções do problema.
F) São feitos 7 testes a nós para verificar se são soluções do problema.
b.
(1.0) Considere a procura em profundidade iterativa e escolha a única opção correcta:
A) O nó A é testado como solução 2 vezes.
B) O nó A é testado como solução 3 vezes.
C) O nó A é testado como solução 4 vezes.
D) O nó B é testado como solução 3 vezes.
E) O nó C é testado como solução 3 vezes.
F) O nó F é testado como solução 1 vez.
c.
(1.0) Considere a procura de custo uniforme e escolha a única opção correcta:
A) O nó F é testado como solução e quando é encontrada a solução há exactamente 3 nós na fila de
nós por testar.
B) O nó F é testado como solução e quando é encontrada a solução há exactamente 2 nós na fila de
nós por testar.
C) O nó E é testado como solução e quando é encontrada a solução há exactamente 3 nós na fila de
nós por testar.
D) O nó E é testado como solução e quando é encontrada a solução há exactamente 2 nós na fila de
nós por testar.
E) O nó D é testado como solução e quando é encontrada a solução há exactamente 2 nós na fila de
nós por testar.
F) O nó D é testado como solução e quando é encontrada a solução há exactamente 1 nó na fila de
nós por testar.
-4-
d.
(1.0) Considere a procura gananciosa e escolha a única opção correcta:
A) O nó com estado D é testado como solução antes do nó com estado E e ambos os nós são testados
como soluções.
B) O nó com estado D é testado como solução antes do nó com estado G e ambos os nós são testados
como soluções.
C) O nó com estado E é testado como solução antes do nó com estado F e ambos os nós são testados
como soluções.
D) O nó com estado G é testado como solução antes do nó com estado E e ambos os nós são testados
como soluções.
E) O nó com estado C é testado como solução antes do nó com estado D e ambos os nós são testados
como soluções.
F) O nó com estado E é testado como solução antes do nó com estado D e ambos os nós são testados
como soluções.
e.
(1.0) Considere a procura A* e escolha a única opção correcta:
A) O nó com estado E é testado como solução antes do nó com estado G e ambos os nós são testados
como soluções
B) O nó com estado D é testado como solução antes do nó com estado F e ambos os nós são testados
como soluções.
C) O nó com estado D é testado como solução antes do nó com estado G e ambos os nós são testados
como soluções.
D) O nó com estado E é testado como solução antes do nó com estado F e ambos os nós são testados
como soluções.
E) O nó com estado D é testado como solução antes do nó com estado E e ambos os nós são testados
como soluções.
F) O nó com estado B é testado como solução antes do nó com estado G e ambos os nós são testados
como soluções.
f.
(1.0) Considere a procura IDA* e escolha a única opção correcta, assumindo que na
primeira iteração o valor do limite é f(A):
A) O nó com estado A é gerado 4 vezes.
B) O nó com estado B é gerado 3 vezes.
C) Os sucessores do nó com estado A são gerados 2 vezes.
D) Os sucessores do nó com estado B são gerados 1 vez.
E) Os sucessores do nó com estado C são gerados 3 vezes.
F) Os sucessores do nó com estado C são gerados 2 vezes.
-5-
6.
(3.0) Considere a seguinte árvore de procura de dois agentes, em que estão assinalados os valores
da função de avaliação para os estados terminais (MAX, oval, MIN rectângulo).
A jogada do Max é a que lhe garante 14 pontos
a.
(1.5) Aplique o algoritmo Minimax com cortes alfa-beta da esquerda para a direita,
indicando, na árvore anterior: a) os valores mínimax para cada nó; b) as folhas visitadas;
c) a jogada escolhida pelo Max.
b.
(1.5) Ordene a árvore anterior de modo a garantir o maior número de cortes alfa-beta,
indicando os cortes alfa-beta efectuados na nova árvore.
-6-
7.
(1.2) Considere a seguinte árvore de procura de dois agentes (MAX oval, MIN rectângulo), em que
os valores f assinalados correspondem a valores da função de avaliação para estados terminais e
em que os nós terminais assinalado com X e Y não têm valor de f atribuído. Quer para X, quer
para Y, existe um conjunto de valores que, se forem atribuído à função de avaliação destes nós,
minimizam o número de nós visitados durante a execução do algoritmo minimax alfa-beta da
esquerda para a direita. Qual o menor destes valores para X e o qual o maior para Y que permitem
realizar os cortes assinalados?
A) X = 4, Y = 2
B) X = 10, Y = 10
C) X = 2, Y = 4
D) X = 3, Y = 10
E) X = 3, Y = 3
F) X = 11, Y = 9
-7-










