
Sistemas Eléctricos e Electromecânicos
Colectânea de Problemas Resolvidos
2010
DEEC – Área de Especialização em Energia
Gil Marques
Maria José Resende
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
2
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
Índice
Problema Nº 1 – Introdução aos Circuitos Resistivos .............................................................................. 5
Problema Nº 2 - Circuitos Resistivos ....................................................................................................... 8
Problema Nº 3 - Circuito RL série (regime permanente) ....................................................................... 10
Problema Nº 4 – Circuitos em AC - Regime Permanente Circuito RLC série ................................. 12
Problema Nº 5 – Circuitos em AC - Regime Permanente + Compensação F.P. .................................... 15
Problema Nº 6 – Circuitos Trifásicos ..................................................................................................... 18
Problema Nº 7 – Circuitos Trifásicos com C. Factor Potência .............................................................. 20
Problema Nº 8 – Circuito Magnético I ................................................................................................... 22
Problema Nº 9 – Circuito Magnético II .................................................................................................. 24
Problema Nº 10 - Circuito Magnético – Cálculo de forças .................................................................... 27
Problema Nº 11 – Cálculo da Força electromecânica numa armadura .................................................. 29
Problema Nº 12 – Problema do conversor electromecânico rotativo elementar .................................... 33
Problema Nº 13 – Circuito Magnético ................................................................................................... 36
Problema Nº 14 – Transformador de distribuição monofásico .............................................................. 38
Problema Nº 15 - Máquinas Eléctricas - Transformador ....................................................................... 43
Problema Nº 16 – Determinação das características de uma máquina de indução a partir do circuito
equivalente.............................................................................................................................................. 45
Problema Nº 17 – Funcionamento da Máquina de indução na zona de pequenos escorregamentos. .... 47
Problema Nº 18 –Máquina de indução controlada com o método u/f. ................................................... 49
Problema Nº 19 – Métodos de arranque da máquina Assíncrona de rotor em gaiola ............................ 52
Problema Nº 20 – O gerador de indução ................................................................................................ 54
Problema Nº 21 - Máquina de Indução ou Assíncrona .......................................................................... 56
Problema Nº 22 – Conversor de frequência rotativo com duas máquinas síncronas ............................. 58
Problema Nº 23 – Motor de Excitação em série..................................................................................... 61
Problema Nº 24 - Maquina DC – Veículo Eléctrico .............................................................................. 63
Problema Nº 25 - Máquina de corrente contínua de Excitação Separada ............................................. 65
Problema Nº 26 - Máquina de Corrente Contínua de Excitação em Série ............................................. 68
Problema Nº 27 Máquina de Corrente Contínua .................................................................................... 70
3
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
4
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
PROBLEMA Nº 1 – INTRODUÇÃO AOS CIRCUITOS RESISTIVOS
Considere o circuito eléctrico representado na figura. Os valores das fontes e resistências encontram-se
representados na mesma figura.
Pretende-se resolver este circuito, isto é, determinar os valores das as corrente tensões e potências em todos
os elementos do circuito.
a) Estabeleça as equações resultantes da aplicação das leis dos nós necessárias para a resolução
do circuito.
Apenas interessam os nós com mais do que dois ramos. Do nó A tira-se:
i1 i 2 i3
do nó B tira-se:
i 2 i3 i1
que é equivalente à obtida na aplicação ao nó A o que ilustra que basta escrever N-1 equações dos nós.
b) Estabeleça as equações resultantes da aplicação das leis das malhas.
Escolham-se as malhas segundo a figura:
5
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
Na malha 1 tem-se:
12 u1 u3 0
Na malha 2 tem-se:
u3 u2 8 0
Se estas duas equações forem verificadas, então a equação que resulta da circulação da malha exterior
também será verificada. Na realidade obter-se-ia:
12 u1 u2 8 0
Que resulta também da soma das duas equações anteriores. Isto quer dizer que esta terceira equação é
linearmente dependente das outras duas. Com efeito:
(12 u1 u3 ) (u3 u2 8) 0
c) Escreva as equações dos elementos do circuito
Tem-se:
us1 12
us 2 8
u1 R1i1
u R i
12
2
u3 R1i 3
Com R1, R2 e R3 os valores indicados na figura
d) Resolva o circuito utilizando o método das correntes fictícias.
Definam-se as malhas
Por inspecção, tem-se:
i J J
1
2
3
i1 J1
i 2 J2
(o que equivalea escrever a lei dos nós no nó A)
Circulando nas malhas e introduzindo ao mesmo tempo as leis dos elementos tem-se:
12 R1J1 R3 (J1 J2 ) 0
R2J2 8 R3 (J2 J1) 0
Colocando na forma matricial, obtém-se:
6
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
R3 J1
12 R1 R3
.
R
R2 R3 J2
3
8
Numericamente obtém-se:
12 11 10 J1
.
8 10 12 J2
Resolvendo o sistema de equações obtém-se como solução:
J1 2
J 2 1
Aplicando a relação entre as correntes de ramo e as correntes de malha, tem-se:
i1 2
i 2 1
i 2 1 1
3
As tensões nos ramos será:
u1 R1i1 1 2 2V
u2 R2i 2 2 1 2V
u R i 10 1 10V
33
3
e) Calcule as potências em todos os ramos.
A tabela apresenta os valores das correntes, tensões e potências.
Elementos
I [A]
U [V]
P [W]
Us1
2
12
-24
Us2
1
8
8
R1
2
2
4
R2
1
2
2
R3
1
10
10
Pode verificar-se que a soma das potências é nula o que verifica o princípio de conservação de energia.
A fonte de 12V está a fornecer potência ao circuito.
As resistências estão a consumir potência eléctrica.
A fonte de 8V está a receber potência do circuito.
7
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
PROBLEMA Nº 2 - CIRCUITOS RESISTIVOS
Considere o circuito representado na figura com os valores das fontes e resistências indicados.
R1 2,5
R1
Vs 12VVs
R2
R2 10
R3 10
R3
R4
R4 20
Js
Js
0,8 A
a) Determine todas as correntes nos ramos e tensões nas fontes utilizando o método das correntes
fictícias
Escolham-se as correntes de malha como se indica na figura. Não é necessário escolher uma corrente de
malha no ramo da fonte de corrente pois esta corrente já é conhecida neste ramo.
Circulando na malha 1, obtém-se:
Vs R1J1 R2 J1 J 2 0
Circulando na malha 2, obtém-se:
R2 J1 J 2 R3 J 2 R4 J 2 J s 0
Colocando na forma matricial, tem-se:
R1 R2
R2
R2
R 2 R3 R 4
J1 Vs
J 2 R 4 J s
Substituindo valores:
12,5 10 J1 12
10 40 J 2 16
Usando a matriz inversa tem-se:
J1 12,5 10
J 2 10 40
1
0,025 12 0,1x12 0,025x16
J1 0,8
12 0,1
J
16 0,025 0,0312 16 0,025x12 0,0312x16
2 0,2
8
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
b) Calcule as potências em todos os elementos e verifique o princípio de conservação de energia.
O cálculo das correntes e tensões nos elementos faz-se a partir do valor das correntes fictícias. Vamos arbitrar
as tensões como se representa na figura e as correntes no sentido do terminal + para o terminal -.
As correntes, tensões e potências serão:
Elemento
Corrente [A]
Tensão [V]
Potência [W]
Vs
I s J1 0,8
Vs 12
Vs I s 9,6
R1
I1 J1 0,8
V1 I1R1 2
V1I1 1,6
R2
I 2 J1 J 2 1
V2 R2 I 2 10
V2 I 2 10
R3
I 3 J 2 0,2
V3 R3 I 3 2
V3 I 3 0,4
R4
I 4 J 2 J s 0,6
V4 R4 I 4 12
V4 I 4 7,2
Js
J s 0,8
VJ s V4 12
VJ s J s 9,6
Verifica-se que, por coincidência, ambas as fontes estão a fornecer ao circuito 9,6W.
Pelo princípio da conservação de energia,
Energia Fornecida Energia Dissipada
9,6 9,6 1,6 10 0,4 7,2
Processo simplificado
Aplicando a conversão Norton-Thevenin, tem-se o circuito:
Cujas equações são:
R1 R 2
R2
R2
J1 Vs
R 2 R3 R 4 J 2 R 4 J s
9
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
PROBLEMA Nº 3 - CIRCUITO RL SÉRIE (REGIME PERMANENTE)
Determine a evolução temporal em regime permanente das tensões e correntes em cada um dos elementos,
quando aplica uma fonte de tensão alternada sinusoidal de valor eficaz Eef 230 V , f 50 Hz .
u R (t )
i
R
R 20
e(t )
e(t ) 2 Eef sin(t )
u L (t )
L
L 300 mH
E E ef e jo º
Z Z R Z L R jL Z e j
2
2
sendo Z R L
e
I
subs.v alores
L
arctan
R
E
Z
E ef e j 0
Z e j
Z
202 250 300 10 3
subs.v alores
E ef j
e
I ef e j
Z
U R R I R I ef e j
250 300 10 3
arctan
20
subs.v alores
subs.v alores
2
I
96
78º
230 j 78
e
2,4 e j 78 A
96
U R 20 2,4 e j 78 48 e j 78 V
U L jL I L e j 90I ef e j L I ef e j 90º
subs. valores U L 2 50 300 103 2,4 e j 9078 225 e j12 V
A evolução temporal das grandezas será, então:
i (t ) 2 2,4 sin(t
78º )
180
u R (t ) 2 48 sin(t
78º )
180
u L (t ) 2 225 sin(t
12º )
180
10
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
[V]
e(t)
uR(t)
i(t) [A]
5
uL(t)
400
4
300
3
200
2
UL
UR
UR
78º
E
100
1
0
0
0
-100
90
180
270
360
450
540
630
720 -1
-2
I
-200
-3
-300
-4
-400
-5
11
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
PROBLEMA Nº 4 – CIRCUITOS EM AC - REGIME PERMANENTE CIRCUITO RLC SÉRIE
Resolução do circuito RLC em série
i
u R (t )
uC (t )
R
C
e(t )
L
Impedância da resistência
ZR R
Impedância da bobine
Z L jL
Impedância do condensador
ZC j
u L (t )
1
C
Como estas 3 impedâncias estão em série
ZT Z R ZC Z L R j 1C jL
1
ZT R j L
C
1º Caso
L
1
0
C
ZT R
I
E
ZT
Circuito com carácter Resistivo
2º Caso
1
L
0
C
ZT
E
ZT R j X
I
Circuito com carácter Indutivo
3º Caso
L
1
C
ZT R j X
I
0
E
ZT
Circuito com carácter Capacitivo
Substituindo valores: Eef 230 V , f 50 Hz , R 20 , C 300 F e L 300 mH
12
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
Z
202 2 50 300 10 3
6
2 50 300 10
1
2
202 842 86
1
L
C arctan 84 77º
arctan
R
20
Z 86 e j 77
A impedância não é uma grandeza sinusoidal
Não faz sentido falar no seu valor eficaz nem na sua evolução temporal!!!
I ef
E ef
Z
230 e j 0
86 e j 77
2,7 e j 77 A
U R ef R I ef 20 2,7 e j 77 53 e j 77 V
U Lef j L I ef L 2,7 e j 90 77 252 e j13 V
U C ef j
1
1
I ef
2,7 e j 77 90 28 e j167 V
C
C
ZT
13º
UC
UC U L
UL
UR
UC
UR
13º
E
13º
I
13
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
[V]
400
e(t)
uR(t)
uC(t)
uL(t)
i(t)
[A]
5
4
300
3
200
2
100
1
0
0
0
-100
90
180
270
360
450
540
630
720
-1
-2
-200
-3
-300
-400
-4
-5
14
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
PROBLEMA Nº 5 – CIRCUITOS EM AC - REGIME PERMANENTE + COMPENSAÇÃO F.P.
Considere o seguinte circuito, alimentado a partir de uma rede de corrente alternada
frequência
Eef 230 V e
f 50 Hz . Considere: R1 R2 ' 0,5 , L1 5 mH , L2 ' 4 mH , LM 50 mH
e
RExt 10 .
R1
L1
R2'
L2'
a
R Ext
LM
b
Determine:
a)
A impedância equivalente do circuito, observada a partir dos terminais ab.
Z 1 é a série de R2 ' , L2 ' e RExt :
R1
L1
a
LM
Z1
b
Z1 R2 'RExt jL2 '
Z1 10,5 j1,26 10,6 e j 6,8
Z 2 é o paralelo de Z 1 e LM :
R1
a
L1
Z2
b
Z2
jL2 Z1
jL2 Z1
15,7 e j 90 10,6 e j 6,8
15,7 e j 90 10,6 e j 6,8
8,34 e j 38,6 6,52 j 5,2
15
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
Finalmente, ZT é a série de R1 , L1 e Z 2 :
a
ZT
b
ZT R1 jL1 Z 2 0,5 j1,57 6,52 j 5,2 7,02 j 6,77 9,75 e j 44
b)
a corrente fornecida pela fonte, bem como as potências activa e reactiva.
I
V
ZT
230 e j 0
9,75 e j 44
23,6 e j 44 A
*
Potência Complexa
S V I 230 e j 0 23,6 e j 44 5 428 e j 44 VA
Potência Activa
P Re S 5 428 cos 44 3 805 W
Q Im S 5 428 sin 44 3 771VAr
Potência Reactiva
o valor da capacidade de um condensador , a colocar à entrada do circuito, de modo a assegurar um factor de
potência unitário.
No problema tem-se:
factor de potência cos 44 0,72 indutivo
e pretende-se que cos ' 1 ' 0º
circuito com um carácter resistivo, globalmente, P 0
e
Q 0.
A potência fornecida por um condensador com uma tensão V c aos seus terminais e que está a ser percorrido
por uma corrente I c , é:
Ic
Vc
Sabendo que a impedância do condensador é Z c j
Tem-se: I c
Vc
Zc
1
C
C Vc e j 90
A potência complexa será então: S c V c I c * C Vc 2 e j 90
16
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
Pc Re S c C Vc 2 cos 90 0
Qc Im S c C Vc 2 sin 90 C Vc 2
o condensador fornece Q
O problema pretende que se dimensione C que forneça toda a energia reactiva que está a ser consumida pelo
circuito; deverá ser então:
Qc Q
C Vc 2 3771
250 C 2302 3771
C 227 F
17
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
PROBLEMA Nº 6 – CIRCUITOS TRIFÁSICOS
Considere o circuito representado na figura
A fontes de tensão constituem um sistema simétrico e equilibrado de tensões de valor eficaz
230 / 400 V e
frequência f 50 Hz . O valor dos parâmetros é:
R1 10
a)
R2 6
C 354F
L 25,5 mH
R3 4,36
Calcule as 3 correntes nas fases bem como a corrente de neutro.
V s1 230 e j 0º
V s 2 230 e j120º
V s3 230 e j 240º
As impedâncias de carga de cada fase são:
Z1 Z R R
subs. valores
Z 1 10
Z 2 Z R Z L R jL
subs. valores
Z 2 6 j100 25,5 103
j
C
subs. valores
Z 3 4,36
Z 3 Z R ZC R
I1
V s1
I2
V s2
I3
Z1
Z2
V s3
Z3
subs. valores
I1
subs. valores
I2
subs. valores
I3
Z 3 10 e j 64,1º
j
100 354 10 6
230 e j 0º
23 e j 0º
10
230 e j 120º
10 e
Z 2 10 e j 52,6º
j 52,6º
230 e j 240º
10 e j 64,1º
A
23 e j 172,6º
A
23 e j 175,9º
A
A corrente de neutro será:
I N I1 I 2 I 3
subs. valores
I N 23 e j 0º 23 e j172,6º 23 e j175,9º
I N 22,8 j 4,4 24,2 e j169º
b)
Desenhe um diagrama vectorial representando as amplitudes complexas das tensões e das
correntes
18
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
c)
Considere agora que todas as cargas são iguais à da fase 2 (carga trifásica equilibrada). Calcule
as amplitudes complexas das correntes nas fases e no neutro. Desenhe o respectivo diagrama
vectorial
Z 1 Z 2 Z 3 Z 10 e j 52,6º
I1
V s1
I2
V s2
I3
Z
Z
V s3
Z
subs. valores
I1
subs. valores
I2
230 e j 0º
10 e j 52,6º
230 e j 120º
10 e
subs. valores
I3
23 e j 52,6º
j 52,6º
230 e j 240º
10 e
j 52,6º
A
23 e j 172,6º
23 e j 67,4º
A
A
A corrente de neutro será:
I N I1 I 2 I 3
subs. valores
I N 23 e j 52,6º 23 e j172,6º 23 e j 67,4º
IN 0
19
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
PROBLEMA Nº 7 – CIRCUITOS TRIFÁSICOS COM C. FACTOR POTÊNCIA
Considere um circuito trifásico simétrico ligado em triângulo, alimentado a partir da rede eléctrica nacional
230/400V, 50Hz. Cada fase da carga pode ser representada pelo seguinte circuito eléctrico:
R
Z
L
R = 2
R
L = 20 mH
a) Determine o valor da impedância Z , de modo a que o valor da impedância total em cada fase
j50º
seja 7e
;
Z L jL 6,3 e j 90
ZR R 2
Z 1 Z L em paralelocom Z R
jLR
12,6 e j 90
1,9 e j 18 1,8 j 0,6
R jL
6,6 e j 72
Z total Z R Z Z1
Z Z total Z R Z1 7 cos 50 j 7 sen 50 2 1,8 j 0,6
Z 0,7 j 4,8 4,85 e j 82
b) Calcule o valor das correntes na linha e as potências activa e reactiva fornecidas pela fonte
I Fase
Como
V Fase
Z total
400
7 e j 50
57 e j 50 A
I Linha 3 I Fase
I Linha 3 57 98,7 A
P 3 VComp ILinha cos 3 400 98,7 cos 50 43 955 W
Q 3 VComp ILinha sin 3 400 98,7 sin 50 52 383 VAr
20
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
c) Determine o valor dos condensadores, a colocar em paralelo com cada fase, de modo a
assegurar um factor de potência de 0,85.
Na nova situação (com condensadores) o circuito consumirá P’ e Q’
e o factor de potência é cos ' 0,85
Será então P P'
e
' 31,8º
Q' S' sin ' P' tan '
Pelo que: Q' 43 955 tan31,8 27 253 VAr
A potência reactiva fornecida pelos condensadores será:
Q Q Q' 52 383 27 253 25 130 VAr
Vcond
Por outro lado, 3 condensadores alimentados com uma tensão
a uma frequência , fornecem
Qcond 3 C Vcond 2 de potência reactiva.
Deverá ser então:
Qcond Q
Como os condensadores deverão estar ligados em , será Vcond 400 V
3 2 50 C 4002 25 130
Tem-se então:
C 167 106 167 F
Represente num diagrama vectorial as tensões e as correntes nas fases, antes e depois de compensar o factor
de potência.
As componentes activas das correntes, antes e depois da compensação, são iguais
I1 cos 50 I '1 cos 31,8
V2
I2
^
I '2
V1I1 50º
^
V1I '1 31,8º
O
31,8º
V1
50º
I3
I '3
^
^
^
^
^
V1V2 V2V3 V1V3 120º
^
I '1
I1I 2 I 2 I 3 I1I 3 120º
I1
I '1 I '2 I '2 I '3 I '1 I '3 120º
^
^
^
V3
21
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
PROBLEMA Nº 8 – CIRCUITO MAGNÉTICO I
Considere o circuito magnético representado na figura.
Considere que o ferro tem permeabilidade relativa igual a
2 cm
10000, que o entreferro é de 1 mm e que a bobine de 400
espiras é percorrida por uma corrente de 1 A.
1 mm
A permeabilidade magnética do ar pode ser aproximada à
i
do vazio.
6 cm
N
rFe 10000
g 1 mm
2 cm
I 1 A
4 cm
2 cm
a)
2 cm
N 400 espiras
ar 0 4 107 H / m
2 cm
Determine os parâmetros do esquema eléctrico equivalente, calculando as reluctâncias
magnéticas.
O circuito eléctrico equivalente é:
Rarmadura
Rentreferro
Rentreferro
Fmm
Rnúcleo
As relutâncias magnéticas são:
Rentreferro
Rarmadura
Rnúcleo
g
ar S
arm
1 103
4 10
rFe ar S
7
2 4 10
4
994718 Ae.Wb 1
6 102
104 4 10 7 2 4 10 4
5968 Ae.Wb 1
núcleo
18 102
17904 Ae.Wb 1
rFe ar S 104 4 10 7 2 4 10 4
As relutâncias magnéticas devidas aos entreferros são cerca de 80 vezes superiores às dos troços em ferro,
mesmo sendo o percurso no entreferro 240 vezes inferior ao no ferro!!
A relutância magnética total será:
22
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
RTotal 2 Rentreferro Rarmadura Rnúcleo 2 013 308 Ae.Wb1
b)
Calcule a relação
2 Rentreferro
.
RTotal
2 Rentreferro 1 989 436
0,988
RTotal
2 013 308
c)
Calcule o fluxo e o campo de indução
B
Fmm N i 400 1 400 Ae
Fmm
400
0,199 10 3 Wb 0,199 mWb
RTotal 2 013 308
B
0,199 103
0,248 T
S
8 10 4
Se se tivesse desprezado a relutância dos troços em ferro face à relutância dos entreferros, os valores seriam:
Fmm
400
0,2 10 3 Wb 0,2 mWb
RTotal 1989436
B
0,2 103
0,251T
S
8 10 4
23
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
PROBLEMA Nº 9 – CIRCUITO MAGNÉTICO II
Considere o circuito magnético representado na figura.
N 400 espiras
rFe 10000
I 1A
ar 0 4 107 H / m
Considere que o ferro tem permeabilidade relativa igual a
10000, que a bobine de 400 espiras é percorrida por uma
corrente contínua de 1 A.
A permeabilidade magnética do ar pode ser aproximada à
do vazio.
Considere duas situações distintas: entreferro de 10 mm e
entreferro de 2 mm
a)
Determine o modelo de circuito magnético, os respectivos parâmetros e os valores dos fluxos e
campo de indução.
2
1
As diversas relutâncias magnéticas para g 2mm são:
l [m]
Rb
Rc1
Rc2
Rar
0,05
0,07
0,01
0,002
S [m2]
0,0008
0,0008
0,0008
0,0008
R [Ae/Wb]
4974
6963
995
1989437
Do circuito magnético equivalente obtém-se:
Ni
Ni
Rc1 Rar Rc 2
R b Rc 2 Rar Rc1 R b 2 2 2
Rc1 Rar Rc 2
2
2
2
Rc1 Rar Rc 2
1
2
2
2
Rc1 Rar Rc 2 2
R b Rc 2 Rar Rc1 R b
2
2
2
Para g 2mm resulta:
24
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
400 3006039 998697 1
400 998697 3006039
2
1 3006039 998697
2 998697 3006039
1
400
400
1 2 0,1 mWb
central 2 0,2 mWb
Bar
Sar
Bcentral
0,1 103
8 10 4
0,1245 T
central 0,2 103
0,1245 T
Scentral 16 10 4
Para g 10mm resulta:
400 10963786 4977571 1
400 4977571 10963786
2
1 10972739 4980555
2 4980555 10972739
1
400
400
1 2 0,025 mWb
central 2 0,05 mWb
Bar
Sar
Bcentral
0,025 103
8 10 4
0,03 T
central 0,05 103
0,03 T
Scentral
16 10 4
25
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
Método alternativo: Este método usa a simetria do circuito magnético para simplificar as equações; o
esquema equivalente é o representado na figura seguinte:
Ni Rar Rc 2 Rb Rc 2 Rar Rc1 Rb Rc1
Ni 2Rar 2Rc 2 2Rb 2Rc1
Substituindo valores para g 2mm :
400 4016673
Substituindo valores para
400 19932167
b)
10 105 Wb 0,1 mWb
g 10mm :
2 105 Wb 0,02 mWb
Repita a) desprezado as relutâncias do ferro face às do ar.
Para g 2mm resulta:
400 2984155 994718 1
400 94718 2984155
2
1 2 0,105 mWb
Para g 10mm resulta:
400 10941902 4973592 1
400 4973592 10941902
2
1 2 0,025 mWb
26
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
PROBLEMA Nº 10 - CIRCUITO MAGNÉTICO – CÁLCULO DE FORÇAS
Considere o seguinte sistema electromagnético. Admita que não há dispersão.
10 cm
R2
R1
c
a
C
10 cm
N1
N2
d
b
1 mm
S 4cm2
N1 200esp.
R1 1
C 1F
rFe 800
N2 100esp.
R2 1
Vab 10V
0 4 x107 Hm 1
Determine:
o valor da relutância magnética do circuito magnético;
l Fe lar
lar
rFe ar S ar S
Rm
4 10 102 2 103
Rm
800 4 x10 7 4 10 4
lar
ar S
Rm
Ae Wb 1
2 103
4 x10 7 4 10 4
5 106 Ae Wb 1
Ae Wb 1
os valores dos coeficientes de auto-indução das bobinas;
L1
N12
2002
0,008H
Rm 5 106
L2
N2 2
1002
0,002H
Rm
5 106
o valor da corrente solicitada à fonte, quando a bobina 2 está em vazio e aos terminais ab é aplicada
uma tensão alternada sinusoidal, com um valor eficaz de 10 V e uma frequência de 50 Hz;
Z eq R jL em paralelocom
1
jC
Z1 R jL 1 j 2 50 0,01 1 j 3,3 e j 72
Zc
1
1
j 3 183 3 183 e j 90
6
jL j 2 50 10
Zeq
Z1 Zc
Z1 Zc
3,3 e j 72
O Condensador é, praticamente, um circuito aberto
27
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
I
V
Z eq
10
3,3 e j 72
3,3 e j 72
A
o valor médio da força a que fica sujeita a peça 2, nas condições da alínea anterior e para valores de
entreferro de 1 mm.
Para I = constante é:
N12
Rm ( x )
F
i 2 L
2 x
F
i2 d
i 2 d N12
i 2 2 d 0S i 2 2 0S 1
L1( x)
N1
N1
2 dx
2 dx Rm ( x) 2
dx 2x
2
2 x 2
L L1
F ( x 1mm )
32
2
7 4 10 4
2 4 10
200
2
Rm ( x )
2x
0S
1
2
10 3
45 N
28
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
PROBLEMA Nº 11 – CÁLCULO DA FORÇA ELECTROMECÂNICA NUMA ARMADURA
Considere o dispositivo do problema nº8 redesenhado na figura
2
abaixo. A área da secção recta é igual a 8cm .
A. Considere a armadura alinhada com o núcleo.
A1. Calcule a relutância magnética do entreferro.
Rar
g
Rentref
0 A
2g
0 A
A2. Determine uma expressão para o coeficiente de auto-indução
da bobina desprezando a dispersão.
Por definição
Li
N
Tem-se
N
Ni
Rm
L
N2
Rm
Desprezando a contribuição do ferro no cálculo da relutância total
L
A N2
N2
0
2Rar
2g
A3. Calcule uma expressão para a força electromecânica que se exerce na direcção vertical, em função
da corrente e da espessura do entreferro. Determine o valor desta força considerando:
Espessura do entreferro igual a 2 mm e a corrente i=1A.
Espessura do entreferro igual a 10 mm e corrente i=1A.
Sendo a corrente imposta, a expressão da força deverá ser determinada através da co-energia magnética.
fx
Wm '
1 2 1 2 dL
Li i
x
x 2
2 dx
fx
1 2 dL
i
2 dx
L em função da espessura do entreferro é
A força será dada por
f x ( x)
L( x )
0 A N 2
2x
1 2
d 1
i 0 AN 2
4
dx x
f x ( x)
1 2
1
i 0 AN 2
4
x2
29
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
f x ( x)
k
x2
i2
com
Substituindo valores:
k
0 AN 2
4
k 4,021 105
para x 2 103 m e i 1A
f x 10,05 N
para x 10 103 m e i 1A
f x 0,40 N
A4. Considere agora que a corrente é alternada sinusoidal de valor eficaz igual a 1A e de frequência
igual a 50Hz.
Com a espessura do entreferro igual a 2 mm, calcule a expressão da força que se exerce sobre a
armadura e o seu valor médio. Compare com o resultado alcançado na alínea A3. Se a frequência
passar para 400Hz, qual a influência no valor médio desta força?
Sendo
i 2I sint
pelo que será:
i 2 2I 2 sin 2 t I 2 1 cos( 2t )
f x ( x)
k
x2
I 2 1 cos( 2t )
f xav ( x )
cujo valor médio é dado por:
k
x2
I2
A expressão do valor da força média, em termos de valor eficaz, é igual à expressão da força na situação de
corrente contínua.
Não depende da frequência, mas depende do valor do entreferro
x.
A5. Considere que esta bobina se encontra alimentada com uma fonte de tensão sinusoidal de
frequência igual a 50Hz e de valor eficaz igual a 60V. Calcule uma expressão para a força
electromecânica que se exerce sobre a armadura. Despreze o valor da resistência da bobina e
considere a espessura do entreferro igual a 2 mm. Se a frequência passar para 400Hz, qual a influência
no valor médio desta força?
Se a bobina se encontrar alimentada por uma fonte de tensão a força terá de ser determinada através da
expressão da energia magnética:
fx
Wm
1 2
x
x 2 L( x )
Sendo desprezável a resistência da bobine, tem-se:
donde
u
d
dt
u dt
u 2U sint
U
2 cost
30
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
Wm
A força poderá ser obtida através da expressão da energia magnética:
AN
L( x ) 0
2x
como já se tinha calculado
pelo que a força será:
fx
2
Wm
obtém-se:
Wm '
2
x
AN 2
1 2
2 L( x )
1 2
1 2x 2
2 L( x ) 2 AN 2
0
Esta força não depende da posição da armadura
x.
0
2
U
1 cos2t
O quadrado do fluxo será dado por
2
Substituindo a expressão do fluxo, tem-se:
fx
f xav
Cujo valor médio é dado por:
2
U
1 cos2t
2
0 AN
1
2
U
A força depende agora da frequência.
2
0 AN
1
Aumentando a frequência 8 vezes (400 Hz) a força diminui 64 vezes.
Para os valores indicados, obtém-se:
Valor médio da força
f xav 227 N
coeficiente de auto-indução
L 0,04 H
com x 2 mm
reactância
X L 12,6
corrente
I
U
4,7 A
X
B. O entreferro é agora constante e igual a 2mm, mas a armadura
y
está desalinhada do núcleo segundo a direcção longitudinal como
g
se mostra na figura.
B
B1. Calcule uma expressão para a força segundo y em função de
C
g e y . Comente o resultado.
x
Nesta situação uma das relutâncias magnéticas do entreferro vai variar
com y. A outra vai ficar constante.
R m1
g
0CB
Rm2
g
0 BC y
O coeficiente de auto-indução será dado por:
fy
L(g, y )
N2
g
g
0CB 0 BC y
1 2 dL(g, y )
I
2
dy
31
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
C. O entreferro é agora constante e igual a g mas a armadura está
desalinhada do núcleo segundo a direcção transversal como se mostra na
figura.
Calcule uma expressão para a força segundo a direcção
z considerando
B
que a bobina se encontra alimentada com uma fonte de corrente contínua
de amplitude igual a 1 A. Comente o resultado. Calcule o valor da força
para g=1mm e I=1A.
Nesta situação ambas as relutâncias magnéticas vão variar com z.
Rar
g
0C B z
O coeficiente de auto-indução será dado por:
L(g, z)
N2
N2
0C(B z)
2Rar
2g
Daqui resulta a força:
fz
1 2 dL
I
2 dz
1 N2
fz I 2
0C
2
2g
Para
g 1 mm e I 1 A
obtém-se fz 1 N
32
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
PROBLEMA Nº 12 – PROBLEMA DO CONVERSOR ELECTROMECÂNICO ROTATIVO ELEMENTAR
Considere um sistema electromagnético constituído por duas bobinas como o indicado na figura
Fr
Fs
Os coeficientes de indução destas bobinas são:
Ls=1H,
Lr=1H,
Msr()=0,9cos().
a) Determine uma expressão para a co-energia magnética.
A expressão para a co-energia magnética toma a forma:
'
Wm
( , i s , i r )
1
1
Ls i s2 Lr i r2 Mi s i r
2
2
Substituindo valores, tem-se:
'
Wm
( , i s , i r )
1 2 1 2
i s i r 0,9i s i r cos
2
2
b) Determine uma expressão para o binário electromagnético.
O binário pode ser obtido através da derivada da co-energia magnética. Obtém-se:
Mem
' ( , i , i )
Wm
s r 0,9i i sin
s r
c) Sabendo que as correntes são dadas por: i s=10A, ir=10A, determine a expressão do binário em
função da posição .
Substituindo os valores das correntes, obtém-se: Mem 0,9i s i r sin 90 sin
33
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
d) Calcule o binário máximo.
O binário máximo será 90Nm obtendo-se para = -/2.
e) Determine a posição de equilíbrio quando o binário exterior aplicado for 45Nm. Analise a estabilidade
dos pontos encontrados
O movimento é regido pela segunda lei de Newton. Para o movimento de rotação, na convenção motor, temse:
I
dm
Mem Mext
dt
O ponto de equilíbrio obtém-se quando o binário acelerador, dado pela diferença entre Mem e Mext se igualar a
zero, ou seja, quando Mem = Mext.
Desenhando ambos os binários no mesmo gráfico, o ponto de equilíbrio obter-se-á quando os gráficos destes
se cruzarem. Obtêm-se os pontos A e B. Para o ponto A tem-se =-/6. Para o ponto B tem-se =-+/6.
Mem
B
-
A
/6
Mext
O ponto A constitui um ponto de equilíbrio estável. Com efeito, se houver uma perturbação no sistema e a
posição se deslocar para a direita, o binário acelerador fica negativo acelerando o rotor no sentido negativo,
isto é, no sentido de regressar ao ponto de equilíbrio. O mesmo se passa para a deslocação à esquerda. A
análise está feita graficamente na figura onde as setas a preto indicam o binário acelerador obtido depois da
perturbação e as setas a azul indicam o sentido de deslocamento do rotor. Pode verificar-se que para o ponto
A, depois da perturbação desaparecer, o sistema regressa ao ponto de equilíbrio. Para o ponto B o sistema
afasta-se do ponto de equilíbrio.
34
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
Mem
B
-
A
-/6
Mext
A figura ilustra o funcionamento do sistema nestas condições. Quando o binário exterior aplicado for nulo, o
ponto de funcionamento será dado por =0, isto é, as duas bobinas estão alinhadas. O binário
electromagnético será nulo também. Quando se aplicar um binário que faça rodar a peça móvel no sentido
negativo de , o rotor rodará para um novo ângulo negativo e surge um binário electromagnético em
oposição que vai equilibrar o sistema. Obtém-se um ponto de equilíbrio de modo que os dois binários sejam
iguais e de sinais opostos. Estas duas situações estão ilustradas nas figuras seguintes.
Fr
Fs
Fs
Fr
Posição de equilíbrio com Mext=0
Posição de equilíbrio com Mext>0
Uma vez que o binário é função da posição, pode fazer-se uma analogia mecânica considerando que tudo se
passa como se existisse uma mola entre o estator e o rotor. Quanto maior for o binário aplicado maior será o
ângulo de equilíbrio.
35
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
PROBLEMA Nº 13 – CIRCUITO MAGNÉTICO
Considere um circuito magnético em que a peça móvel se desloca perpendicularmente às linhas de
força do campo. Admita para dimensões da figura os seguintes valores:
g=1 mm
d=10 cm
I=15 cm
N=500 espiras
Determine, em função da coordenada x:
a) a expressão da relutância magnética do circuito;
d
I
g
I
g
I
x
x0
d
x
2
Sd l
x
S
Para ,
d
x0 Sd l
2
Então
S( x ) I d x para
Admitindo que
Fe
0x
d
2
d
l
2
Para , 0 x
0x
d
2
e
d
S( x ) I d x
2
S( x) S(0)
para
d
x0
2
Rmag Rmag
ar
2g
2 10 3
10,61 103
Rmag Rmag
ar
0 S x 4 10 7 15 10 2 10 10 2 x 10 10 2 x
para
x
x0
Ae Wb 1
d
2
36
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
b) a expressão do coeficiente de auto-indução da bobine;
admitindo linearidade magnética
L( x )
N2
Rmag ( x )
N 2 0 l d x
23,6 10 102 x
2g
H
c) A expressão da co-energia magnética ou da energia magnética armazenada na bobine;
admitindo linearidade magnética
Wmag f , x
1 1 2
2 L( x )
Wmag ' f i , x
1
L( x ) i 2
2
N 2 0 l d x 2
i
4g
2651 10 102 x
J
d) O valor e sentido da força a que fica sujeita a peça móvel.
d
Wmag '
dx
d N 2 0 l d x 2
i
dx
4g
d
2
2651 10 10 x
dx
2651 N
f
Força que tenderá a colocar a peça móvel por forma a que seja S d l . Note-se que o valor desta força é
independente de x.
37
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
PROBLEMA Nº 14 – TRANSFORMADOR DE DISTRIBUIÇÃO MONOFÁSICO
Considere um transformador monofásico com as seguintes características nominais:
SN=100kVA
10kV/400V
No ensaio em curto-circuito, aplicando a tensão ao enrolamento de 10kV, obtiveram-se os seguintes
resultados:
U=500V
I=10A
P=1kW
No ensaio em vazio, aplicando a tensão aos terminais de 400V, obteve-se:
U=400V
I=2,5A
P=250W
NOTA: Os valores usados neste problema estão próximos dos valores encontrados nos transformadores de
distribuição trifásicos.
a) Calcule os valores das correntes nominais do transformador.
Pela definição de potência nominal, tem-se:
S N U1N I1N U 2 N I 2 N
donde:
I1N
100000
10 A
10000
I 2N
100000
250 A
400
b) Qual o valor da tensão de curto-circuito em percentagem?
A tensão de curto-circuito é o valor da tensão a aplicar a um dos enrolamentos de modo a obter-se a
sua corrente nominal quando o outro enrolamento se encontrar em curto-circuito. Neste caso,
atendendo aos dados do enunciado, para o enrolamento de 10kV aplicou-se 500V para se obter 10A
que é o valor da corrente nominal deste enrolamento. A tensão de curto-circuito será igual a 500V. Em
percentagem da tensão nominal será:
U cc
500
5%
10000
que é um valor vulgar para transformadores desta dimensão.
c) Qual o valor da corrente em vazio em percentagem?
A corrente em vazio foi medida no ensaio em vazio. Como esta medida foi efectuada no enrolamento
de 400V que tem uma corrente nominal de 250A, tem-se:
I0
2,5
1%
250
38
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
d) Determine os parâmetros do circuito equivalente deste transformador reduzido ao
enrolamento de 10kV.
O circuito equivalente de um transformador reduzido ao primário representa-se como:
Rcc jXcc
I1
U1 R1fe
I'2
I2
U'2
jX1m
U2
A determinação dos parâmetros deste circuito é feita através dos ensaios em curto-circuito e em vazio.
Para o ensaio em curto-circuito, atendendo à forma como foi feito, tem-se:
Rcc jXcc
I1
U1 R1fe
I'2
I2
U'2
jX1m
Como U2=0, tem-se U’2=0, e o circuito fica:
Rcc jXcc
I1
U1 R1fe
I'2
jX1m
O ensaio em curto-circuito permite determinar o ramo Rcc +jXcc. Para isso recorre-se a uma
simplificação: a impedância do ramo de magnetização é muito superior em valor óhmico à impedância
do ramo de curto-circuito. Esta simplificação permite desprezar a corrente que circula no ramo de
magnetização neste ensaio. Note-se que em vazio, à tensão nominal, a corrente de magnetização é da
ordem de 1%. À tensão reduzida de 5% será ainda menor, pelo que esta simplificação se torna
perfeitamente admissível. Assim o circuito ficará:
I1=10A
Rcc jXcc
U1=500V
P1=1000W
O valor da resistência Rcc será dada por:
Rcc
P
I2
1000
10 2
10
39
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
O valor da impedância será:
Z cc
U 500
50
I
10
A reactância será dada por:
X cc 50 2 10 2 49
Note-se que este ramo é essencialmente indutivo. O termo indutivo Xcc é quase igual ao módulo da
impedância Zcc.
Para o ensaio em vazio, tem-se:
I1=0
U1 R1fe
Rcc jXcc
I2=2,5A
I'2
U2=400V
U'2
jX1m
Aplicando ao secundário uma tensão de 400V vai corresponder U’2=10000V. À corrente 2,5A vai
corresponder uma corrente de 0,1A dado que a razão de transformação é U1/U2=25. O circuito ficará:
Rcc jXcc
R1fe
I'2=0,1A
jX1m P=250W
U'2=10000V
Agora pode fazer-se uma outra simplificação: a queda de tensão no ramo de curto-circuito pode ser
desprezada face à tensão aplicada. Note-se que esta queda de tensão será aproximadamente igual a
50×0.1=5V que é muito inferior a 10000V aplicados. Assim, tem-se o circuito:
I'2=0,1A
R1fe
jX1m P=250W
U'2=10000V
Pode determinar-se os parâmetros a partir das potências activa e reactiva. A potência activa será
representada na resistência e a potência reactiva na reactância. Assim:
R1 fe
U 2 10000 2
400k
P
250
A potência reactiva é dada por:
Q S 2 P2
10000 0,12 250 2
968 var
40
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
X 1m
U 2 10000 2
103k
Q
968
Se, para a representação da magnetização do transformador, em vez do circuito RL em paralelo se
tivesse utilizado o circuito RL série, ter-se-ia:
Rs
Zs
P
I2
250
0,12
25k
U 10000
100k
I
0,1
X s Z 2 R 2 96,8k
e) Calcule o rendimento no ponto de carga nominal com factor de potência unitário. Considere
que a tensão do secundário é igual à tensão nominal.
O rendimento é igual à potência de saída a dividir pela potência de entrada que é igual à potência de
saída mais as perdas. Neste caso, para a potência de saída igual à potência nominal, tem-se:
f)
100000
98,77%
100000 250 1000
Determine a carga para a qual se obtém o rendimento máximo. Qual o valor do rendimento
correspondente.
A carga para a qual o rendimento é máximo será obtida quando as perdas no cobre forem iguais às
perdas no ferro. Assim, a corrente I’2 correspondente será determinada por:
2
Rcc I 2' P0
donde:
I 2'2
250
25
10
donde I 2' 5 A , o que corresponde a metade da carga nominal.
A esta carga correspondem ¼ das perdas no cobre. As perdas em vazio mantêm-se em 250W. Assim o
rendimento será:
50000
99,01%
50000 250 250
que é ligeiramente superior ao rendimento no ponto nominal. Conclui-se assim que o rendimento para cargas
superiores à carga nominal é uma função aproximadamente constante, embora ligeiramente decrescente.
41
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
g) Determine o valor da regulação de tensão com carga nominal e factor de potência cos=0,7
indutivo. Considere que a tensão no secundário é igual à tensão nominal.
Com factor de potência igual a cos=0,7 (sin=0,71) indutivo, o diagrama vectorial será:
U1
U'2
RccI'2
jXccI'2
I'2
A que corresponde o vector U1 igual a
U1 10000 Rcc jX cc 100,7 j 0,71 10418 j 272V
Este vector tem um módulo de U1=10421V. A regulação de tensão será dada por:
Re g
10421 10000
4,04%
10421
42
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
PROBLEMA Nº 15 - MÁQUINAS ELÉCTRICAS - TRANSFORMADOR
Uma caldeira eléctrica monofásica apresenta uma potência de 2 kW e tem uma tensão eficaz de alimentação
de 115 V. É necessário dimensionar um transformador monofásico, uma vez que a rede eléctrica nacional,
230/400 V, 50 Hz, é a única fonte de alimentação disponível.
a) Tendo disponível as 3 fases da rede e o neutro, mostre, esquematicamente, como ligaria o
transformador à rede;
Fase 1
Fase 2
Fase 3
Fase 1
Fase 2
Fase 3
Transformador
Neutro
Transformador
Neutro
b) Considerando como ideal o transformador necessário, determine a sua relação de transformação e
as correntes eficazes do primário e secundário;
Ligação Fase-Neutro
V1N 230 V
V2N 115 V
V
I
230
k 1N 2N
2
V2N I1N 115
V2N I2N 2 103 I2N 17,4 A
I
k 2N 2 I1N 8,7 A
I1N
Ligação Fase-Fase
V1N 3 230 V 400 V
V2N 115 V
k
400
3,5
115
I1N 5 A
I 2N 17,4 A
c) Sabendo que os dois enrolamentos são semelhantes e que apresentam iguais resistências
r1 r2 1 , e iguais coeficientes de fugas, 1 2 1 mH , determine a potência activa absorvida
num ensaio em curto-circuito através do secundário;
Ensaio cc efectuado através do secundário
43
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
I 2N
r1 '
r2
X1'
X2
V2cc
r2 1
X 2 2 0,314
r
r1 ' 1 0,25
k2
X1'
I 2N
Z eq 2
V2cc
X1
k
2
0,0785
Z eq r1 ' r2 j ( X 1 ' X 2 ) 1,25 j 0,3925 1,31 e j17
V 2cc Z eq 2 I 2 N 1,31 e j17 x 17,4 22,8 e j17 V
P2cc V2cc I 2 N cos 22,8 x 17,4 x cos 17 380 W
Se o ensaio cc fosse efectuado através do primário
I1N
r1
X1
r2 '
X2'
V1cc
r2 ' r2 k 2 4
r1 1
X 1 1 0,314
X 2 ' X 1 k 2 1,256
Z eq1 r1 r2 ' j ( X 1 X 2 ' ) 5 j1,57 5, 24 e j17
V 1cc Z eq1 I 1N 5,24 e j17 x 8,7 45,6 e j17 V
P1cc V1cc I1N cos 45,6 x 8,7 x cos 17 380 W
d)
Determine o rendimento do transformador ideal e o rendimento do transformador real, isto é,
considerando as resistências e as fugas referidas na alínea c).
ideal 100%
Pout PN 2000 W
Pin Pout Pperdas 2000 380 2380 W
P
2000
real out
84 %
Pin
2380
44
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
PROBLEMA Nº 16 – DETERMINAÇÃO DAS CARACTERÍSTICAS DE UMA MÁQUINA DE INDUÇÃO A PARTIR DO
CIRCUITO EQUIVALENTE.
Uma máquina assíncrona de 400V, 50Hz, dois pares de pólos, tem o circuito equivalente indicado na figura.
Sabe-se que o ponto nominal de funcionamento se obtém com a velocidade de N=1491rpm.
R1
I1
jXcc
R2
I’’2
r1+rm
1-s R2
s
U1
j(X1+Xm)
rm 0,018
X m 0,890
R1 4,4 103
R2 1,8 103
X cc 44,3 103
r1 rm 22,1 103
X1 X m 911,9 103
a)
Determine o valor da corrente em vazio I 0
Em vazio tem-se
I0
I0
I ' '2 0 pelo que será:
U1
r1 rm j X1 X m
231
3
22,1 10
3
j 911,9 10
245,5 e j88,6 A
Corrente fortemente indutiva.
b)
Para o ponto nominal obtenha:
I ' '2 , I 1 , cos , e o binário
f
60 1500 rpm
p
Velocidade de sincronismo
Ns
Velocidade nominal
N n 1491 rpm
Escorregamento nominal
sn
Ns Nn
0,6 %
Ns
45
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
I ' '2n
Através do esquema equivalente obtém-se:
I ' '2n
U1
R2
R1
j X cc
sn
231
758 e j8,4 A
3
4,4 103 1,8 10 j 44,3 103
0,006
I 1n I ' '2n I 0
Através do esquema equivalente obtém-se:
I 1n 758 e j8,4 245,5 e j88,6 839 e j25,7 A
cos n cos 25,7 0,9
O factor de potência será:
n
O rendimento é:
Pout n
Pinn
A potência mecânica útil à saída da máquina é:
Pout n 3
Poutn 3
A potência eléctrica activa à entrada da máquina é:
1 sn
R2 I ' '2n 2
sn
1 0,006
1,8 1037582 514 kW
0,006
Pinn 3 U1 I1n cos n
Pinn 3 2318390,9 524 kW
n
Poutn
Pinn
98%
O binário útil é:
M outn
ou
M outn
c)
3 1 sn
R2I ' '2n 2
n sn
Poutn
n
Determine as perdas em vazio,
M out n
514 103
3292 Nm
2
1491
60
P0 , e no cobre em regime nominal, PCn
As perdas em vazio são as associadas ao ramo transversal.
P0 3 r1 rm I02
P0 3 21,3 103 245,52 4,3 kW
As perdas no cobre são as associadas aos enrolamentos quando percorridos pela corrente nominal.
PCn 3 R1 R2 I ' '2n2
PCn 3 4,4103 1,8103 7582 10,7 kW
46
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
PROBLEMA Nº 17 – FUNCIONAMENTO DA MÁQUINA DE INDUÇÃO NA ZONA DE PEQUENOS
ESCORREGAMENTOS.
Conhece-se o catálogo de um fabricante de motores eléctricos de indução de rotor em curto-circuito. A tabela
apresenta as características de alguns destes motores.
PN
Rendimento
N
[rpm]
Factor
de
I [A]
Potência
1,1
80,6
1430
0,78
2,5
2,2
86,4
1425
0,83
4,4
3
87,5
1430
0,83
6
4
89,3
1445
0,83
7,8
5,5
90,7
1465
0,85
10,3
7,5
91,7
1465
0,85
13,9
11
92,6
1470
0,8
21,4
15
92,9
1465
0,82
28,4
22
94,3
1475
0,84
40,1
Pretende-se escolher um motor para accionar uma grua, como se indica na figura.
Considere que o conjunto “Tambor – multiplicador de velocidade” tem rendimento igual a 98%.
a) Calcule a potência no veio do motor e escolha o motor mais apropriado.
A potência na massa a ser içada é determinada por:
P Fv 9,8 1000 1 9800W
No veio da máquina será:
Pm
9800
10000 W
0,98
Tendo em atenção a tabela, deverá ser escolhido o motor de 11 kW.
b) Calcule a velocidade de rotação da máquina.
Tendo em consideração que a máquina estará um pouco abaixo da potência nominal a sua velocidade de
rotação deverá ser diferente da velocidade de rotação no ponto nominal, isto é, 1470 rpm.
47
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
Dado que a velocidade de rotação não varia muito com a carga, a velocidade a calcular deverá ser um pouco
superior a 1470 rpm, podemos considerar que a potência é proporcional ao binário. Na zona de
escorregamentos baixos, pode considerar-se que a potência é função linear com a diferença entre a
velocidade de sincronismo e a velocidade de rotação. Assim, a velocidade de escorregamento (Velocidade de
sincronismo –velocidade de rotação) será:
11kW
30rpm
10kW
X
A velocidade de escorregamento será:
X
10
30 27,27
11
Ou seja
N=1500-27,27=1472,7 rpm
c) Calcule a velocidade de rotação da máquina quando elevar uma carga com metade da massa.
Nesta situação a potência será reduzida para metade.
11kW
30rpm
5kW
X
A nova velocidade de escorregamento será:
X
5
30 13,63
11
A velocidade de rotação será agora:
N=1500-13,63=1486,4 rpm
48
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
PROBLEMA Nº 18 –MÁQUINA DE INDUÇÃO CONTROLADA COM O MÉTODO U/F.
Considere um motor eléctrico de indução de 55kW, 400V, 50Hz, com dois pares de pólos e os seguintes
parâmetros do seu circuito equivalente em estrela:
r1 24m ;
r2 27m ;
x1 220m ;
x 2 200m ;
RFe 150 ;
Xm 6
A velocidade nominal da máquina é 1485 rpm.
Esta máquina vai ser alimentada através de um conversor electrónico com a lei de regulação U/f = constante.
Faça as simplificações que achar necessárias e verifique os erros cometidos.
a) Calcule o binário máximo para 50Hz e para 25 Hz com U/f constante
O binário máximo é calculado em função dos parâmetros do circuito equivalente em ângulo.
Conversão dos parâmetros do ramo transversal:
150 j 6
r m jX m
150 j 6
Parâmetro
r m 0,24
X m 5,99
a:
a a 1
x1
Xm
a 1,0367
Parâmetros do circuito equivalente para 50 Hz:
R2 a 2 r '2
R1 a r1 R1 0,02449
X cc a x 1 a 2 x 2
R 2 0,029
X cc 0,443
r1 r m 0,2636
x 1 X m 6,21
M max
Binário máximo:
f 50 Hz U1 231 V
M max
3 pU12
2 R1 R12 X cc 2
3 2 2312
1087 Nm
2 100 R1 R12 X cc 2
2
f 25 Hz U1
231
V
2
231
32
2
M max
100
X
2
R1 R12 cc
2
2
2
1028 Nm
49
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
1200
1000
M [Nm]
800
600
400
200
0
0
500
1000
1500
N [rpm]
Considere que o motor está a accionar uma carga cujo binário é constante e independente da
velocidade:
b) Para a carga referida anteriormente calcule: I 0 ,
I0
U1
r1 r m j x 1 X m
Velocidade de sincronismo
Ns
I 0 1,57 j 37,12 37,2 e j 87,57
N 1485 rpm
Escorregamento
s
U1
R
R1 2 j X cc
s
I 1 I ' '2 I 0
A
f
60 1500 rpm
p
Velocidade
I ' '2
I ' '2 , I 1 , I1ef , cos , M em , P2 , P1 e
Ns N
0,01
Ns
I ' ' 2 77,16 j 11,7 78 e j 8,6
I 1 78,7 j 49 92,6 e j 31,8
M em
A
A
cos cos 30 0,85
M em
3 p R2
I ' '2 2
s
3 2 0,029
782 338 Nm
100 0,01
2 50
52,5 kW
2
Pem M em m M em 1 s syn
Pem 338 1 0,01
P1 3U1 I1 cos
P1 3 231 92,6 0,85 54,5 kW
P
em
P1
52,5
96,2%
54,5
50
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
c) Considerando que o binário de carga se mantém constante calcule a velocidade da máquina quando
alimentada a 25Hz.
f
f 25 50
2
se
como
U / f constante
X 25
X 50
2
U 25
U 50
2
para escorregamentos pequenos (zona linear da característica electromecânica) tem-se:
3p s
U1 2
R2
M em
U1 2
3 p R2
2
s
R2
2
R1
X cc
s
M em
Será então:
f 25 Hz
U1
231
115,5 V
2
x 1 X m 3,105
X cc 0,2215
Como o binário exigido pela carga é constante e independente da velocidade a equação em
s
a resolver,
será:
M em 25 M em 50
cujas soluções são:
3p R 2U 12
s 2 R12 X cc 2 s 2R1R 2
M em50
s 1 0,0204
e
R 2 0
2
s 2 0,83
A solução s2 corresponde ao funcionamento a escorregamento elevado, pelo que a solução do problema é:
N rot (1 0,0204) 750 734,7 rpm
s 1 0,0204
Alternativamente, utilizando a expressão aproximada para escorregamentos pequenos (zona linear da
característica electromecânica) tem-se:
M em
3p s
o valor é
R2
U 1 2
s 0,02
N rot 1 0,02 750 735 rpm
51
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
PROBLEMA Nº 19 – MÉTODOS DE ARRANQUE DA MÁQUINA ASSÍNCRONA DE ROTOR EM GAIOLA
Considere uma máquina de indução de rotor em gaiola com as seguintes características: PN 5,5 kW ,
U N 400 V , f 50 Hz . Esta máquina está construída para funcionar em regime normal, ligada em
triângulo.
Sabe-se que no arranque directo absorve da rede 66A apresentando um cos 0,6 . Nesta situação tem um
tempo de arranque em vazio igual a 1,5 seg.
a)
Qual a corrente e o tempo de arranque que se irão verificar se a máquina for ligada em estrela.
U Fase Z ( s ) I Fase
Do esquema equivalente obtém-se:
No arranque
s 1
Uc
arranque em Y
3
I F arr 3 I F arrY
Na fase
IL 3 IF
I L arr 3 I L arrY
Na linha
M U F 2
t arr
I F arrY I L arrY
(para um mesmo valor de
Pelo que deverá ser:
b)
Z (1) I FarrY
U c Z (1) I Farr
arranque em
como:
Z ( s ) Z (1) = constante
66
22 A
3
s) M 3 M
Y
1
t arrY
3
t arrY 3 1,5 4,5 seg
Dimensione uma reactância para colocar em série de modo a reduzir a corrente de arranque
para 22A quando a máquina arranca em triângulo. Calcule a tensão aplicada à máquina nos
instantes iniciais e estime o valor do tempo de arranque.
em
I Larr 66 A
A impedância equivalente em estrela desta situação é:
Pretende-se que
Z
400 3
3,5
66
I Larr 22 A com introdução de uma reactância em série.
Será então:
Z jX
400 3
3 Z
22
52
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
Z jX 3 Z
jX
sin 0,8
como cos 0,6
0,6Z 2 0,8Z X 2 3 Z
X
VS
9 0,36 0,8 Z
Como
c)
M U
1
tarr
Z
X 7,5
Vmotor
A tensão aos terminais do motor será:
2
V motor
U
tU 2 1
U2
2
Z
VS
Z jX
3,5
231 77 V
10,5
2
231
tU1
1,5 13,5 seg
77
A máquina vai ser posta em serviço utilizando um transformador auxiliar. Determine o valor
nominal da tensão do secundário deste transformador de modo a reduzir a corrente pedida à
rede para 22A quando a máquina arranca em triângulo. Estime o tempo de arranque. Considere
o conceito de transformador ideal.
I motor
I rede
U rede
U motor
Z
Admitindo que o transformador é ideal e tem uma relação de transformação
m , a tensão aplicada ao motor,
U motor , será:
U motor
U rede
m
Com base no esquema equivalente e para um mesmo valor de escorregamento tem-se
a tensão foi reduzida de um factor
U motor I motor ; se
m , o mesmo acontecerá à corrente.
I
I motor arr
m
Com base no conceito de transformador ideal
I
I rede arr
m2
Se
U rede 231 V
2
Como M U
1
tarr
I motor m I rede ; a corrente pedida à rede será então:
I
66
m 2 arr
3
I rede 22
U motor
U
tU 2 1
U2
2
U rede
3
m 3
231
133 V
3
2
231
tU1
1,5 4,5 seg
133
53
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
PROBLEMA Nº 20 – O GERADOR DE INDUÇÃO
Uma máquina de indução é representada pelo circuito equivalente por fase.
I1
I2"
4,3m
j55m
I0
22,75m
1,8m
231V
j0,65
s
Admita que a máquina tem dois pares de pólos e que a frequência é igual a 50 Hz.
Para a velocidade de rotação de 1510 rpm calcule as seguintes grandezas: corrente em vazio, corrente
equivalente no rotor, corrente no estator, factor de potência, potência no eléctrica estator, potência mecânica
no veio, rendimento
Resolução
Para a velocidade de 1510 rpm corresponde o escorregamento de:
s
1500 1510
0,0067
1500
Como o escorregamento é negativo, a máquina encontra-se a funcionar como gerador.
a) A corrente em vazio será dada por:
I0
231
12,4 j 355 355e j 88 º ( A)
0,0227 j 0,65
b) A corrente equivalente do rotor vale:
I 2''
231
834 j173 851e j 168 ,3º
0,0018
0,0043
j 0,055
0,0067
c) A corrente do estator será:
54
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
I1 I0 I2'' 821 j 527 976e j147 ,28 º
O diagrama vectorial das correntes será:
I2"
U1
I0
I1
d) O factor de potência será:
cos cos(147,28) 0,84
e) A potência trocada pelo estator será:
P1 3 231 976 cos 567kW
f) A potência mecânica no veio
P2 3R2
1 s ' '2
I 591kW
s 2
g) O rendimento será dado por:
P
1 96,3%
P2
55
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
PROBLEMA Nº 21 - MÁQUINA DE INDUÇÃO OU ASSÍNCRONA
Um motor assíncrono trifásico de 4 pólos, apresenta os seguintes valores nominais:
PN 5 kW
sN 4 %
N 90 %
cosN 0,85
Estando o motor alimentado por uma rede trifásica 230/400 V a 50 Hz, determine:
a) Os valores da velocidade em vazio e em condições nominais
0 S
vazio
nominal
2 200
157,1 rad s 1 1500 rpm
p
4
N 1 sN S 1 0,04 157,1 150,7 rad s 1 1440 rpm
b) O valor do binário desenvolvido, a sua velocidade de rotação e escorregamento, quando acciona
uma carga cujo binário resistente varia linearmente com a velocidade de rotação, de acordo com a
expressão:
Mcarga( )
0,12
10
Mmotor
N , MN
Mcarga( )
Binário nominal do motor
P
5000
MN N
33,2 Nm
N 150,7
Equação da recta do motor
M
MN 0
S 5,2 815
N s
No ponto de funcionamento será: Mcarga Mmotor
0,12
Mcarga
10
Mmotor 5,2 815
1
153,7 rad s 1468 rpm
Mmotor Mcarga 15,6 Nm
O escorregamento correspondente a esta velocidade é s
s 1500 1468
2,1%
s
1500
56
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
c) Sendo o binário de arranque do motor, em ligação triângulo, de 20 Nm, justifique se o grupo
motor+carga poderá arrancar estando o motor ligado em estrela.
20
6,7 Nm
3
Marr Y
Marr 20 Nm
0,12
Marr carga
10
10 Nm
0
Como
Marr carga Tarr Y
o grupo NÃO arranca
Mmotor
N , MN
Mcarga( )
d) Para o ponto de funcionamento nominal, determine a amplitude complexa da corrente que o motor
solicita à rede
P
5000
Pabs N N
5555 W
N
0,9
Independentemente do tipo de ligação do motor ( ou Y), tem-se sempre:
Pabs 3 VComposta ILinha cos
Em regime nominal será:
5555 3 400 ILinha 0,85
ILinha 9,4 A
Como cos 0,85 e a máquina é um circuito indutivo,
arccos 0,85 31,8º
A amplitude complexa da corrente (valor eficaz) é: I Linha 9,4 e
j 31,8
A amplitude complexa da corrente (valor máximo) é: I Linha máx
A
2 9,4 e j 31,8 A
57
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
PROBLEMA Nº 22 – CONVERSOR DE FREQUÊNCIA ROTATIVO COM DUAS MÁQUINAS SÍNCRONAS
Um laboratório de ensaios de material para aeronáutica dispõe de um conversor de frequência de 50 Hz para
400 Hz . Este conversor é constituído por um motor síncrono com um par de pólos ligado à rede de 400V,
50 Hz e de um gerador síncrono de 8 pares de pólos. Ambas as máquinas, ligadas pelo veio, rodam à
velocidade de 3000 rpm. Esta velocidade é imposta pelo número de pares de pólos do motor ligado à rede de
50 HZ. Ambas as máquinas têm a mesma potência nominal, 1,5 MW e a mesma reactância síncrona
X s 0,15 , sendo desprezável a resistência. O valor da tensão nominal é 400 V .
a)
O gerador vai alimentar uma carga igual à carga nominal com factor de potência igual a
cos 0,7 indutivo. A excitação foi regulada de modo a ter-se a tensão nominal aos terminais
do gerador.
Faça um diagrama vectorial que represente o gerador nesta situação e calcule o valor da força
electromotriz em vazio.
O circuito equivalente, na convenção gerador é o que se indica na figura seguinte.
jXs
I
U
Ef
No regime de carga nominal
cos 0,7 indutivo
45,6º
O Gerador vai fornecer
P e Q . O diagrama vectorial em convenção GERADOR é:
I 2165 e j 45,6 A
b)
I IN 2165 A
E f U jX s I 463 j 227,3 515,8 e j 26,1 V
A excitação do motor foi regulada para que em regime de meia carga se tenha factor de
potência unitário.
Faça um diagrama vectorial que represente o motor a meia carga e calcule o valor da força
electromotriz em vazio. Calcule a potência máxima que o motor pode fornecer ao gerador com
esta corrente de excitação de modo a não perder o sincronismo.
58
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
A que corresponde o diagrama vectorial, também na convenção gerador
admitindo
I
I
No regime de meia carga
100%
IN
IN
2
PN
1,5 106
2165 A
400
3UN
3
3
2165
1083 A
2
Atendendo ao diagrama vectorial, e utilizando o teorema de Pitágoras, tem-se:
2
Ef
P 3
400
0,15 10832 281,4 V
U 2 X sI 2
3
U Ef
sin
Xs
com
2
2
Pmax
2
Pmax 1,3 MW
( O sinal negativo resulta de se ter um funcionamento motor em convenção gerador)
c)
Mantendo a potência no veio igual a meia carga, a excitação do motor é agora ajustada de modo
que esta forneça à rede uma potência reactiva de 500kVAr. Calcule de novo a alínea anterior.
Pmec
P
Q
admitindo 100%
Por outro lado,
M
Pmec P 3 U I cos
Q 3 U I sin
Usando convenção gerador, tem-se:
400
1,5
106 3
I cos
2
3
400
500 103 3
I sin
3
I 1300 A
146,3º
o diagrama vectorial em convenção GERADOR é:
59
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
U
jXsI
I
Ef
I 1300 e j (146,3) A
E f U jX s I 339 j162,21 375,8 e j 25,5 V
400
Pmax 3
d)
3
375,8
0,15
1,736 MW
A excitação do motor é agora ajustada de modo que este absorva da rede 500kVAr. Calcule de
novo a potência máxima do motor.
Comparando com o caso anterior, a corrente e o ângulo são iguais em módulo, apenas se tem o simétrico do
ângulo. Alterando o ângulo como anteriormente, tem-se a figura.
I
U
jXsI
Ef
I 1300 e j (18033,7) A
E f U jX s I 122,77 j162,21 203,4 e j 52,9 V
400
Pmax 3
3
203,4
0,15
0,94 MW
Da comparação entre c) e d) conclui-se que, se o motor fornecer potência reactiva à rede, a sua estabilidade
vem melhorada; é estável para uma maior gama de potência fornecida.
60
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
PROBLEMA Nº 23 – MOTOR DE EXCITAÇÃO EM SÉRIE
Um motor série, com uma resistência do induzido de ra 0,2 e com uma resistência do indutor série de
rf 0,1 encontra-se alimentado sob uma tensão DC de 220 V . A reacção do induzido é desprezável e o
circuito magnético não se encontra saturado.
À velocidade de 1000 rpm o motor absorve uma corrente de 50 A
Representação esquemática da máquina série
Enrolamento de
Campo ou Excitação
Lf
rf
La
Enrolamento do
Induzido
ra
E
Representação esquemática da máquina série quando alimentada em DC
Ia
r ra r f 0,3
N 1000 rpm
U 220 V
E
a) Qual o binário electromagnético desenvolvido?
Como se desconhecem as perdas mecânicas
E Ia M m
Cálculo de E
U r Ia E
E 205 V
O binário será:
M
205 50
97,9 Nm
2
1000
60
b) Qual será a velocidade desta máquina se a corrente consumida passar para metade?
61
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
E N
Numa máquina de corrente contínua
Na máquina série e admitindo linearidade magnética, também se tem
Ia
E N Ia
Pelo que será
Cálculo de E1
U r Ia1 E1
E1 220 0,3 25 212,5 V
E
Será então:
E1
N Ia
N1 Ia1
N1
1000 50 212,5
2073 rpm
205 25
c) Na situação da alínea b) determine qual o novo valor do binário desenvolvido.
E I
M1 1 a1
m1
M1
212,5 25
24,5 Nm
2
2073
60
d) Determine o rendimento do motor nas duas situações anteriores.
P
útil
Pabs
Pabs U Ia
Pútil M m
Pabs 220 50 11 kW
Pútil 97,9 1000
2
10,252 kW
60
93,2%
Pabs 1 220 25 5,5 kW
Pútil 1 24,5 2073
2
5,319 kW
60
1 96,7%
O rendimento melhora na segunda situação porque são menores as perdas de Joule nos enrolamentos r Ia2
e não se estão a considerar as perdas mecânicas.
62
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
PROBLEMA Nº 24 - MAQUINA DC – VEÍCULO ELÉCTRICO
Um veículo eléctrico possui uma massa de 20 000 kg. Pretende-se acelerar este veículo com um valor
constante de 1,1 m s 2 desde o arranque até uma velocidade constante de 20 m s 1 . O veículo está equipado
com um motor de comutação (motor de corrente contínua excitação independente) através de uma caixa de
transmissão com uma relação de 1 m por cada 21 rad de rotação do motor. O motor está alimentado por uma
fonte de energia eléctrica contínua de valor variável e apresenta uma resistência do induzido de 0,04 e
desenvolve um binário de 5,5 N m quando absorve uma corrente de 2 A . Despreze perdas mecânicas e
magnéticas. Recorde que Pmec M F v e dimensione:
a) A potência nominal do o motor
O motor deverá ter, no mínimo, uma potência nominal de:
Pmec F v m a v 20 000 1,1 20 440 000 W 440 kW
b) O valor do binário desenvolvido e da corrente solicitada à fonte, para atingir a aceleração desejada;
P
440 000
M mec
1 048 Nm
420
M kIa ; na máquina de excitação independente M Ia 1 048
5,5
Ia Ia 381 A
2
c) Para alimentar o motor, dispõe-se de duas fontes contínuas de valor variável; uma pode fornecer até
600 V e outra 1200 V. Qual utilizaria?
V k raIa
V raIa 600 0,04 381
213 rad s 1 equivalente a
k
5,5 2
V raIa 1200 0,04 381
430 rad s 1 equivalente a
k
5,5 2
v 213
1
10 m s 1
21
v 430
1
20,5 m s 1
21
ou
P600 600 381 228,6 kW PN a tensão da fonte não permite uma transmissão de potência suficiente para
alimentar o motor
P1200 1200 381 457,2 kW PN
Suficiente para alimentar o motor
d) Se utilizasse a fonte de 600 V, explique onde poderia actuar para que o veículo atingisse a
velocidade de 20 m s 1 .
63
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
De acordo com
ser:
k
V raIa
V raIa
dever-se-ia baixar o fluxo de excitação para poder atingir 420 rad s 1 . Deveria
k
600 0,04 381
1,39 Nm A1
420
Nestas circunstâncias deveria ter-se em atenção que a corrente do induzido seria muito superior.
e) Se arrancasse o motor com uma tensão de 400 V qual seria a corrente de arranque? Qual seria o
procedimento mais correcto para o arranque?
V
400
No arranque tem-se Ea k 0 e portanto será: V raIarranque Iarranque
10 000 A .
ra 0,04
O arranque do motor deveria ser efectuado elevando lentamente a tensão da fonte variável para que a
corrente não atinja valores tão elevados.
64
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
PROBLEMA Nº 25 - MÁQUINA DE CORRENTE CONTÍNUA DE EXCITAÇÃO SEPARADA
Uma máquina DC de 25 kW, funciona a uma velocidade constante de 3000 r.p.m., com uma corrente de
excitação constante iexc 10 A . Nestas condições tem-se E a 125 V . A resistência do induzido é de
0,02 e a do indutor é de 1 . Considere que as perdas de atrito são constantes e iguais a 1 kW .
Determinar a corrente do induzido, a potência, o rendimento, o binário e o factor de carga, quando a tensão
aos terminais do induzido é:
a)
a)
128 V
Va 128 V
b)
Ea 125 V
124 V
A máquina está a funcionar como motor
iexc 10 A
Ra 0,02
Ia
N 3000 rpm
Vexc
Va 128 V
Va Ra Ia Ea
Ea 125 V
Ia
rexc 1
128 125
150 A
0,02
Potência absorvida pelo motor Pabs Va I a Vexc i exc 128 150 1 10
2
19,3 kW
Perdas nos enrolamentos
penr Ra I a 2 rexc i exc 2 0,02 150 2 1 10 2 0,55 kW
Potência electromagnética
Pa Ea Ia 125 150 18,75 kW Pabs penrolament os
Potência útil do motor
Pútil Pmec Pa patrito 18,75 1 17,75 kW
Rendimento do motor
P
17,75
útil
92%
Binário electromagnético
Pabs
19,3
P
18,75 103
Mem a
59,7 Nm
3000
2
60
65
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
P
17,75 103
Mútil útil
56,5 Nm
3000
2
60
Binário útil
P
17,75 103
f .c. útil
71 %
PN
25 103
Factor de Carga
b)
Ea
V 124 V
não se altera de (a) para (b) pois
Ea 125 V
N
e
são constantes
A máquina está a funcionar como gerador
Ra 0,02
iexc 10 A
Ia
N 3000 rpm
Va 124 V
Ea Ra Ia Va Ia
Potência útil do gerador
Ea 125 V
Vexc
125 124
50 A
0,02
Pútil V a Ia 124 50 6,2 kW
Perdas no enrolamento do induzido
Potência electromagnética
rexc 1
penr induzido Ra Ia 2 0,02 502 0,05 kW
Pa Ea Ia 125 50 6,25 kW Pútil penr induzido
Potência mecânica absorvida pelo gerador
Pmec Pa patrito 6,25 1 7,25 kW
Potência total absorvida pelo gerador
Pabs Pmec penr indutor 7,25 103 1 102 7,35 kW
66
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
Rendimento do gerador
Binário electromagnético
Binário fornecido ao gerador
Factor de Carga
Pútil
6,2
84,3%
Pabs 7,35
P
6,25 103
Mem a
19,9 Nm
3000
2
60
P
7,25 103
M mec
23,1 Nm
3000
2
60
P
6,2 103
f .c. útil
25 %
PN
25 103
67
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
PROBLEMA Nº 26 - MÁQUINA DE CORRENTE CONTÍNUA DE EXCITAÇÃO EM SÉRIE
Um motor SÉRIE roda a 1500 rpm e absorve uma corrente de 13,6 A sob 230 V. A resistência do induzido é
igual a 0,77 e a do indutor 1,06 .
a) Calcular a f.e.m. do motor
R Ra rexc 1,83
I
N 1500 rpm
Ea
V 230 V
V Ra I Ea Ea 230 1,83 13,6 205 V
b) Calcular o binário útil no veio
Como se desconhecem as perdas mecânicas,
Pútil Pmec Pa Ea I 205 13,6 2788 kW
P
Tútil Ta a
Binário
2788
17,7 Nm
1500
2
60
c) O motor é ligado a uma fonte de 115 V. Calcular a sua velocidade para uma corrente de 13,6 A
V Ra I Ea
I
não se alterou
Na máquina série, I
V Ra I k N
Ra I não se alterou
I não se alterou
Das expressões anteriores conclui-se que
não se alterou
V RaI Ea N
68
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
Ea V 230
N
V 230
Ea V 115
NV 115
205
1500
115 1,83 13,6 NV 115
NV 115 660 rpm
d) Calcular o binário nas condições da alínea anterior
Genericamente tem-se:
P
Mútil útil
P
E I
kN Ia
a a a
k ' Ia
2
N
60
sendo k '
60 k
2
Na máquina de excitação série e admitindo linearidade magnética,
I
M k' ' I 2
Como a corrente não se alterou da alínea (b) para a alínea (c), o binário também não se alterará.
69
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
PROBLEMA Nº 27 MÁQUINA DE CORRENTE CONTÍNUA
Uma máquina de corrente contínua excitação independente é caracterizada pelos seguintes valores:
PN 2,0 kW
VN 230 V
NN 1500 rpm
Ra 2,0
La 19 mH
IN 10 A
a) Determine a velocidade do motor, quando no induzido é aplicada uma tensão de 115 V e este acciona
uma carga com binário constante e igual a metade do valor nominal.
Ea k
Máquina independen te
Ea
Ainda não é possível calcular
Ea
pois desconhece-se a corrente absorvida
P
P
E I
k Ia
M mec a a a
k Ia
Máquina independen te
M Ia
Tem-se então:
MN
IaN
MN 2
Ia
I
Ia a 5 A
2
V RaIa Ea Ea 115 2 5 105 V
Nas condições nominais tem-se:
VN RaIaN EaN EaN 230 2 10 210 V
Como Ea , será então:
EaN
Ea
NN
N
N
NN
750 rpm
2
b) Qual o valor do binário máximo que o motor pode desenvolver a 3000 r.p.m. e com a tensão nominal,
sem entrar em regime de sobrecarga?
70
Sistemas Eléctricos e Electromecânicos - Problemas – 2010
Como à velocidade de 3000rpm se está na zona de enfraquecimento de campo (3000rpm >> 1500 rpm) a
potência máxima da máquina é a sua
potência nominal. Para não entrar em sobrecarga deverá ser
Pmáx PN
P
Mmáx N
2000
6,4 Nm
3000
2
60
c) Estime o valor máximo da corrente de arranque, admitindo que ao induzido é aplicada a tensão
nominal.
No arranque tem-se N 0
Ea 0
A corrente de arranque é limitada apenas pela resistência equivalente do induzido
V
Ia arranque N
Ra
Ia arranque 115 A
e) O valor da tensão a aplicar no induzido da máquina para que, em vazio, esta rode a 1000 rpm.
Em vazio
Ia 0 0
Ea 0 V0
Viu-se anteriormente que, na máq. independente Ea . Será então:
EaN ________
NN
Ea0 ________
N0
Ea 0
205 1000
137 V V0
1500
71






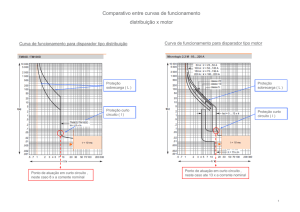




![1. [5] Um circuito integrado precisa de uma tensão de alimentação](http://s1.studylibpt.com/store/data/000892095_1-927da8bea174b016f37ec8deb83e76f0-300x300.png)