Capítulo IV: As Antenas Filamentares

42
Capítulo IV: As Antenas Filamentares - o Dipolo Elétrico
As antenas filamentares estão entre as mais antigas, simples baratas e, em muitos casos, as
mais versáteis em diversas aplicações.
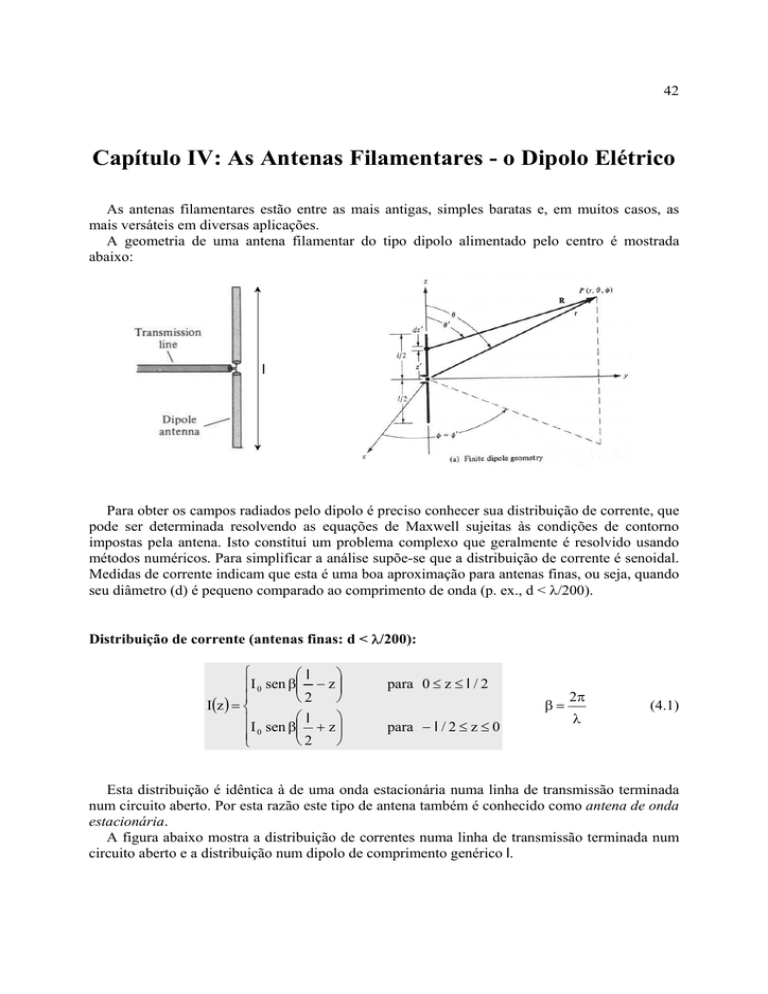
A geometria de uma antena filamentar do tipo dipolo alimentado pelo centro é mostrada
abaixo:
l
Para obter os campos radiados pelo dipolo é preciso conhecer sua distribuição de corrente, que
pode ser determinada resolvendo as equações de Maxwell sujeitas às condições de contorno
impostas pela antena. Isto constitui um problema complexo que geralmente é resolvido usando
métodos numéricos. Para simplificar a análise supõe-se que a distribuição de corrente é senoidal.
Medidas de corrente indicam que esta é uma boa aproximação para antenas finas, ou seja, quando
seu diâmetro (d) é pequeno comparado ao comprimento de onda (p. ex., d < λ/200).
Distribuição de corrente (antenas finas: d < λ/200):


l
I 0 sen β − z 


2
I(z ) = 
I sen β l + z 


 0

2

para 0 ≤ z ≤ l / 2
β=
para − l / 2 ≤ z ≤ 0
2π
λ
(4.1)
Esta distribuição é idêntica à de uma onda estacionária numa linha de transmissão terminada
num circuito aberto. Por esta razão este tipo de antena também é conhecido como antena de onda
estacionária.
A figura abaixo mostra a distribuição de correntes numa linha de transmissão terminada num
circuito aberto e a distribuição num dipolo de comprimento genérico l.
43
As figuras abaixo ilustram a distribuição de corrente em dipolos de diversos comprimentos:
l << λ
l = λ/2
λ/2 < l < λ
λ < l < 3λ/2
Cálculo dos campos radiados (na região de campos distantes):
Para calcular os campos radiados por uma antena filamentar considera-se que ela é formada
por uma sucessão de dipolos infinitesimais (elementos de corrente). O campo total é a soma
(integral) dos campos devidos a cada elemento infinitesimal.
A configuração geométrica para o cálculo dos campos distantes é mostrada na figura abaixo:
44
O campo radiado por um elemento infinitesimal de corrente é dado por:
dE θ = η 0
I(z )
2λR
dz sen θ je − jβR .
(4.2)
Na região de campos distantes, onde R // r e θ′ ≅ θ, são feitas as seguintes aproximações:
Termos de amplitude:
R≅r
Termos de fase:
R ≅ r - z cosθ.
Desta forma:
dE θ = η 0
I(z )
2λr
dz sen θ je − jβr e jβz cos θ .
O campo total é dado por Eθ = ∫dEθ, ou seja:
E θ = η0
E θ = η0
sen θ − jβr l / 2
je ∫ I(z ) e jβz cos θ dz
−l / 2
2λr
I 0 sen θ
2λr
l/2
 0

l

l

je − jβr  ∫ sen β + z  e jβz cos θ dz + ∫ sen β − z  e jβz cos θ dz .
−l / 2
0
2

2



Calculando as integrais e agrupando os termos obtém-se finalmente:
(4.3)
45
  βl
 βl  

 cos cos θ  − cos  
I
 2   je − jβr

E θ = η0 0   2
.

2πr 
sen θ




(4.4a)
Na região de campos distantes Hφ = Eθ/η0. Portanto:
  βl
 βl  

 cos cos θ  − cos  
I
 2   je − jβr

Hφ = 0   2
.


2πr
sen θ




(4.4b)
As equações (4.4a) e (4.4b) permitem calcular os campos distantes Eθ e Hφ radiados por uma
antena linear fina, de comprimento l, simétrica e alimentada pelo centro. A forma do diagrama de
campo é dada pelo fator entre colchetes.
Eis alguns exemplos de diagramas de campo para antenas com diferentes comprimentos:
dipolo de meia onda
dipolo com l = 1,5λ
dipolo de onda completa
Densidade de potência e intensidade de radiação:
O valor médio da densidade de potência é dado por: Pmed =
1
E (t ) H (t ) dt = Re{E
∫
T
2
1
θ
φ
θ
}
H *φ .
T
Usando (4.4a) e (4.4b) obtém-se:
2
Pmed
  βl

 βl  
cos cos θ  − cos  
2 
ηI

 2 
= 0 0  2
. [W/m2]
2 2 

8π r
sen θ




A intensidade de radiação é dada por:
(4.5)
46
2
U(θ, φ) = r 2 Pmed
  βl
 βl  

cos cos θ  − cos  
2 
ηI
 2 

= 0 0  2
.
2 

8π
sen θ




[W/sr]
(4.6)
Para obter a potência total radiada pela antena pode-se integrar (4.5) através da superfície de
uma esfera de raio r na região de campos distantes:
PT = ∫
S
r
r
2π π
η0 I 02
2
Pmed ⋅ dS = ∫ ∫ Pmed r sen θ dθ dφ =
φ = 0 θ =0
4π
∫
  βl
 βl 

cos cos θ  − cos 
π 
 2 
2

0
sen θ
2
dθ . (4.7)
A integral anterior pode ser avaliada tanto analítica quanto numericamente, o que permite
calcular a potência total radiada pela antena.
Resistência de radiação:
Como R r = 2PT / I 02 , a resistência de radiação pode ser obtida diretamente a partir do cálculo
da integral em (4.7).
Diretividade:
Sabendo-se que D = Umax/Umed e Umed = PT/4π, pode-se calcular a diretividade também a partir
da integração em (4.7).
A figura abaixo mostra a diretividade e a resistência de radiação em função do comprimento
da antena (normalizado em relação ao comprimento de onda).
47
Por exemplo, para o dipolo de meia onda a diretividade é de 1,64 (ou 2,15 dBi) e a resistência
de radiação é de 73 Ω.
Resistência de entrada:
A impedância de entrada é definida como a razão entre a tensão e a corrente nos terminais de
entrada da antena. A parte real desta impedância é a resistência de entrada a qual, para uma
antena sem perdas, corresponde à sua resistência de radiação. Esta é calculada dividindo o dobro
da potência total radiada pela corrente máxima na antena ao quadrado. Entretanto, dependendo do
comprimento da antena, o máximo de corrente pode não corresponder ao ponto de alimentação.
Isto acontece, por exemplo, para l = 3λ/4, λ, 2λ, etc. A figura abaixo ilustra este fato.
Para referir a resistência de radiação aos terminais de entrada, deve-se igualar à potência nos
terminais de entrada à potência no máximo de corrente:
1
2
R in I in2 =
1
2
R r I 02 ,
(4.8)
onde Rr é a resistência de radiação referida ao máximo de corrente, Rin é a resistência de radiação
referida aos terminais de entrada, I0 é a corrente máxima e Iin é a corrente nos terminais de
entrada. Pode-se mostrar que, para l ≥ λ/2, estas correntes estão relacionadas por:
 βl 
I in = I 0 sen   .
2
(4.9)
De (4.8) e (4.9) obtém-se finalmente:
R in =
Rr
 βl 
sen  
2
2
.
(para l ≥ λ/2)
(4.10)
48
A aplicação de (4.10) para um dipolo de onda completa (l = λ), por exemplo, dá uma
resistência de entrada infinita (Rin = ∞). Isto implica que a antena seria vista como um circuito
aberto pelos circuitos de alimentação a ela conectados e não haveria assim transferência de
energia destes circuitos para antena, tornando a radiação impossível. Na realidade a resistência de
entrada desta antena é elevada mas não infinita uma vez que a distribuição senoidal de corrente é
apenas uma aproximação. Na prática, a corrente nos terminais de alimentação nunca será nula, de
forma que a radiação é possível.
O Dipolo de Meia Onda
Uma das antenas mais usadas é o dipolo de meia onda, que consiste em dois segmentos
metálicos alinhados, com comprimento total igual a λ/2.
⇒ Distribuição de corrente: a partir de (4.1), com l = λ/2 e lembrando que β = 2π/λ, tem-se:
π

I(z ) = I 0 sen ± β z  = I 0 cos β z .
2

(4.11)
⇒ Campos distantes: A partir de (4.4a) e (4.4b) obtém-se:
 π

 cos cos θ  
I
  je − jβr
E θ = η0 0   2

2πr 
sen θ




e
 π

 cos cos θ  
I
  je − jβr
Hφ = 0   2
.

2πr 
sen θ




(4.12)
49
⇒ Diagrama de radiação:
⇒ Resistência de radiação: a partir de (4.7), a potência total radiada pelo dipolo de meia onda é
dada por:
2
 π



cos
cos
θ


η0 I 02 π   2

dθ .
PT =
∫
4π 0
sen θ
(4.13)
Pode-se mostrar que o valor da integral entre colchetes é igual a 1,218. Desta forma:
PT =
1,218 η 0 I 02
4π
=
1
2
R r I 02 ,
R r ≅ 73 Ω .
ou seja,
⇒ Diretividade: a diretividade de uma antena é dada por D =
U max
U med
(4.14)
= 4π
U max
PT
.
De (4.6), com l = λ/2 tem-se
 π

cos cos θ  
2 
ηI

U(θ, φ) = 0 0   2
2 

8π
sen θ




2
⇒
U max =
η 0 I 02
8π 2
.
(4.15)
De (4.14) e (4.15) tem-se, portanto:
D = 4π
U max
PT
 η I2
= 4π 0 0
2
 8π
⇒ Abertura efetiva:

4π


2
 1,218η 0 I 0
Ae =
λ
⇒
D = 1,64 ou 2,15 dBi .
(4.16)
0,361 λ
2
4π




D
⇒
A e = 0,131 λ2 = 0,522 l 2
0,361 λ
50
⇒ Impedância de entrada: para um dipolo de meia onda sem perdas, a parte real da impedância
de entrada é idêntica à sua resistência de radiação (uma vez que o máximo de corrente coincide
com seus terminais de alimentação). Para calcular a parte reativa da impedância de entrada devese integrar a densidade de potência radiada na região de campos próximos (numa superfície
fechada envolvendo a antena e muito próxima a ela). Para o dipolo de meia onda este cálculo
resulta numa parte reativa de 42,5 Ω. Assim:
Z in = 73 + j42,5 Ω
(4.17)
De forma a casar o dipolo com uma linha de transmissão (p. ex., com Z0 = 50 Ω), em primeiro
lugar deve-se fazer sua impedância de entrada puramente resistiva. Para isto pode-se usar um
capacitor de modo a eliminar a parte indutiva de sua impedância na freqüência de operação.
Entretanto, na prática é mais comum encurtar ligeiramente o comprimento do dipolo de forma a
torná-lo ressonante, isto é, com impedância de entrada puramente resistiva. Por exemplo, um
dipolo fino, com l ≅ 0,49λ, tem impedância de entrada puramente real (Zin ≅ 70 Ω).
Tabela comparativa:
Antena isotrópica
Diretividade Diretividade [dBi] HPBW
1
0
----
Ae
0,08λ2
Dipolo infinitesimal
1,5
1,76
90°
0,12λ2
Dipolo λ/2
1,64
2,15
78°
0,13λ2
Rr [Ω]
---2
2
80 π (l / λ )
73
A Antena Cilíndrica (dipolos espessos)
Até aqui foram consideradas as antenas finas (filamentares), cujos diâmetros são desprezíveis
comparados ao comprimento de onda. Neste caso, a distribuição de corrente é senoidal. Para uma
antena espessa, entretanto, o diâmetro não é desprezível (por exemplo, d > λ/200) e a distribuição
senoidal de corrente não é exata. Para obter a distribuição exata de corrente devem-se resolver as
equações de Maxwell sujeitas às condições de contorno impostas. Pode-se mostrar que o
diâmetro (ou raio) finito tem um efeito maior sobre a impedância de entrada da antena, com
pouca influência sobre seu diagrama de radiação.
51
Influência do raio finito sobre a distribuição de corrente:
Como ilustração, a figura abaixo mostra a distribuição de corrente num dipolo de onda
completa (l = λ) cujo raio representa um centésimo do comprimento de onda (a = 0,01λ). A curva
tracejada corresponde à distribuição senoidal e a curva contínua foi obtida através da resolução
do problema usando uma técnica numérica (método dos momentos).
Observa-se uma grande discrepância entre as duas distribuições no ponto de alimentação da
antena. A distribuição senoidal prevê um zero de corrente neste ponto, o que implicaria numa
impedância de entrada infinita, o que não é correto. A distribuição obtida com o método dos
momentos aproxima-se bem mais da distribuição real.
Influência do raio finito sobre o diagrama de radiação:
A figura abaixo mostra os diagramas de radiação em função da relação de comprimento total
para o diâmetro (l/2a) para diversas antenas cilíndricas de diferentes comprimentos.
l
=∞
2a
l
= 450
2a
l
= 50
2a
l
2a
= 8,7
52
Observa-se que o efeito principal do aumento do raio é o preenchimento de alguns dos zeros
do diagrama e o cancelamento de alguns dos lobos menores (particularmente para l = 1,5λ).
Influência do raio finito sobre a impedância de entrada:
As figuras abaixo mostram a variação da resistência e da reatância de entrada de um dipolo
espesso em função de seu comprimento elétrico (l/λ) para diversos valores da relação entre seu
comprimento e seu diâmetro (l/2a).
l/λ
l/λ
Pode-se observar que a antena de meia onda será ressonante (Xin = 0) para comprimentos
ligeiramente inferiores a λ/2, os quais diminuem com o aumento da espessura da antena. Neste
caso, a espessura tem pouca influência sobre o valor da resistência de entrada. Por outro lado,
para o dipolo de onda completa (l = λ), tem-se uma variação muito grande da resistência de
entrada com a espessura da antena. Observa-se também que antenas muito curtas (l << λ) têm
reatância de entrada fortemente capacitiva.
A figura abaixo permite ver com mais clareza a variação da impedância de entrada de uma
antena fina em função de seu comprimento (l/λ) e de sua espessura ( a 2 / λ ).
53
a 2 /λ =
Uma representação alternativa consiste em mostrar a resistência e a reatância de entrada em
diagramas espirais no plano complexo como função da espessura da antena. Na figura a seguir, os
eixos horizontal e vertical correspondem, respectivamente, à resistência e à reatância de entrada
da antena. A espiral em linha contínua representa a variação de impedância de entrada para uma
antena fina (l/a = 4000) e a espiral em linha tracejada para um dipolo espesso ((l/a = 120). Em
ambos os casos, o semicomprimento do dipolo é variável sobre a espiral, desde l/2 = 0,1λ até
l/2 = 1,1λ. Obviamente, para uma antena de comprimento fixo, esta variação pode representar o
comportamento de sua impedância de entrada com relação à freqüência.
54
Observa-se que as variações de impedância de entrada com a freqüência são bem menores
para a antena espessa do que para a antena fina. Isto mostra que se pode aumentar a largura de
faixa de operação de um dipolo simplesmente aumentando seu diâmetro.
Impedância mútua entre antenas lineares
Sejam duas antenas próximas, conforme a figura abaixo:
antena 1
antena 2
I1
I2
V1+
_
+
_ V2
55
A presença de uma antena altera a impedância de entrada da outra e vice-versa. O sistema
pode ser representado por uma rede de quatro terminais (quadripolo) descrita pelas seguintes
relações tensão-corrente:
V1 = Z11 I1 + Z12 I 2
V2 = Z 21 I1 + Z 22 I 2
,
(4.18)
onde Z11 é a impedância própria da antena 1, Z22 é a impedância própria da antena 2 e Z12 = Z21 é
a impedância mútua entre as antenas.
Na presença da antena 2, a impedância de entrada da antena 1 (Zin 1) é dada por:
Z in 1 =
I
= Z11 + Z12  2
I
I1
 1
V1

.


(4.19)
Para casar a antena 1 com seu circuito de alimentação, Zin 1 deve estar casada com a
impedância da linha. Isto mostra que o casamento deve levar em conta não somente a impedância
da antena isolada no espaço mas também seu acoplamento com antenas próximas.
As figuras abaixo mostram as curvas de resistência mútua (R21) e reatância mútua (X21) de
dois dipolos de meia onda em diferentes configurações como função da distância entre eles.
dipolos lado a lado
dipolos colineares
56
Verifica-se que a configuração lado a lado apresenta efeitos mútuos mais intensos já que as
antenas estão posicionadas na direção de máxima radiação. Como esperado, observa-se que os
valores de impedâncias mútuas diminuem com o aumento da separação entre as antenas para
ambas as configurações.
Exercício: Dois dipolos de meia onda idênticos estão colocados lado a lado e são alimentados
com correntes de mesmo valor. Se a separação entre eles é de 0,35λ, calcule a impedância de
entrada de cada um deles.
Solução: De (4.19), com correntes iguais, tem-se que Zin 1 = Z11 + Z12.
Da figura precedente (dipolos lado a lado) com d = 0,35λ obtém-se: Z12 = 25 - j38 Ω.
Como Z11 = 73 + j42,5 Ω, vem: Z in 1 = 98 + j4,5 Ω . (Idem para Zin 2)
Antenas lineares em presença de planos condutores: o método das imagens
Até aqui se considerou a radiação de antenas no espaço livre ilimitado. Na prática, entretanto,
as antenas estão geralmente colocadas sobre ou a pouca distância da terra ou de alguma outra
superfície refletora. A presença destas superfícies pode alterar significativamente as propriedades
de radiação da antena assim como sua impedância de entrada.
Antena radiando em presença da terra:
A figura abaixo mostra uma antena colocada a uma distância h acima da terra. Para simplificar
a análise, considera-se a terra como um plano condutor perfeito.
57
No ponto P1 chegam duas ondas: uma vindo diretamente da antena (onda direta) e outra que
chega após sofrer uma reflexão no ponto R1 (onda refletida). A onda refletida pode ser vista como
uma onda emitida por uma fonte virtual colocada a uma distância h abaixo do plano de terra
(fonte imagem). Para um ponto P2, o ponto de reflexão é R2 mas a fonte virtual é a mesma. Isto é
verdadeiro para todos os pontos acima do plano condutor. Desta forma, a análise de uma antena
próxima a um plano condutor pode ser feita substituindo o plano por fontes virtuais que
representam as reflexões neste plano. Acima do plano condutor, os campos gerados pelo sistema
equivalente são idênticos aos do sistema real. Abaixo do plano condutor, os campos são nulos.
A figura a seguir ilustra o método das imagens. A direção das setas indica o sentido da
corrente na antena real e na antena imagem.
Como ilustração dos efeitos da terra na radiação de uma antena, a figura abaixo mostra os
diagramas de radiação (plano vertical) de um dipolo de meia onda colocado verticalmente a
diversas distâncias h acima da terra (considerada perfeitamente condutora).
Os efeitos sobre a impedância do dipolo são mostrados na figura abaixo.
58
O monopolo de quarto de onda
Consiste num fio metálico retilíneo, com comprimento igual a λ/4, colocado sobre um plano
condutor infinito (plano de terra). O campo produzido na região acima do plano de terra pelo
monopolo e por sua imagem é o mesmo que seria produzido por um dipolo de meia onda sem a
presença do plano de terra.
⇒ Diagrama de radiação: acima do plano de terra, é idêntico ao do dipolo de meia onda.
 π


θ
 
cos
cos

η0 I 02   2

U(θ, φ) =
2 

8π
sen θ




2
(0° ≤ θ ≤ 90°)
⇒ Resistência de radiação: como o monopolo de quarto de onda só radia no hemisfério
superior, a potência total radiada corresponde à metade da potência radiada pelo dipolo de meia
onda alimentado com a mesma corrente. Desta forma, sua resistência de radiação será à metade
da do dipolo.
PT =
0,609 η 0 I 02
4π
=
1
2
R r I 02 ,
R r ≅ 36,5 Ω .
ou seja,
(4.20)
⇒ Diretividade : a partir de (4.16) e (4.20), tem-se que a diretividade do monopolo é o dobro da
do dipolo:
D = 4π
U max
PT
 η I2
= 4π 0 0
2
 8π

4π


2
 0,609η 0 I 0




⇒
D = 3,28 ou 5,16 dB .
(4.21)
59
⇒ Abertura efetiva: A e =
λ2
4π
D
⇒
A e = 0,261 λ2 = 4,176 l 2
0,511 λ
0,511 λ
⇒ Impedância de entrada: assim como com a resistência de radiação, a impedância de entrada
do monopolo é a metade da do dipolo.
Z in =
73 + j42,5 Ω
2
⇒
Z in = 36,5 + j21,25 Ω .
(4.22)
Antenas do tipo monopolo têm larga aplicação prática, por exemplo, em radiodifusão,
telefonia móvel, radioamadorismo, etc. Na transmissão de rádio em ondas médias (de 300 kHz a
3 MHz), o monopolo consiste numa torre alta colocada diretamente sobre a terra. Neste caso, para
melhor simular um plano metálico, geralmente a antena é instalada em regiões de solo úmido, de
baixa resistividade. Além disso, usa-se uma malha de terra feita com fios de cobre dispostos
radialmente a partir da base da antena (tipicamente 120 radiais de comprimento em torno de λ/4).
Para monopolos instalados num veículo, a própria estrutura metálica deste atua como plano de
terra. Para obter um diagrama onidirecional, pode-se instalar a antena no teto do veículo. Caso se
deseje um diagrama direcional, é possível instalá-la nas laterais do veículo ou nos pára-choques.
A alimentação do monopolo pode ser feita através de um cabo coaxial tendo seu condutor externo
conectado ao plano de massa e o condutor interno conectado ao fio metálico.
Em algumas aplicações, as configurações mostradas abaixo podem ser utilizadas.
O plano de terra circular tem diâmetro de cerca de meio comprimento de onda. Na figura do
centro, o plano circular foi substituído por quatro condutores radiais. A inclinação destes
condutores permite alterar os níveis de impedância e o ângulo de cobertura dos diagramas
verticais.