Última Aula
6872 - Fundamentos de
Eletrônica
Elvio J. Leonardo
Lei de Ohm
Associação de Resistores
Análise de Circuitos
Universidade Estadual de Maringá
Departamento de Informática
Bacharelado em Ciência da Computação
Leis de Kirchhoff
Circuitos Equivalentes de Thévenin e Norton
2014
2
Roteiro
Capacitor
Capacitor & Indutor
Capacitor
Componente com 2 terminais que armazena energia em
um campo elétrico
Indutor
Contém duas placas condutoras separadas por dielétrico
Capacitor e Indutor em Corrente Contínua
Capacitor e Indutor em Corrente Alternada
– Placas de filme ou disco metálico (alumínio)
– Dielétrico (isolante) de vidro, cerâmica, ar, papel, mica, etc.
Não dissipa energia (como os resistores)
– Energia é armazenada em campo elétrico
Transformador
Unidade de Capacitância: Farad [F], pelo cientista inglês
Michael Faraday
Valor da capacitância e tolerância
– Indicado no corpo do componente, com números impressos ou
faixas de cores
3
4
Capacitor & Indutor
Capacitor
Capacitor
Símbolos
– Fixo
Capacitor & Indutor
Relação Tensão/Corrente em um capacitor
Fixo com polaridade
Variável
– ௗ௩ ௧
ௗ௧
» Em regime, a corrente no capacitor é nula se a tensão é constante
௧
ଵ
– ௧ τ τ
బ
Associação de Capacitores
– Série:
ଵ
ଵ
భ
ଵ
మ
⋯
ଵ
– Paralelo: C ଵ ଶ ⋯
5
6
Capacitor & Indutor
Indutor
Capacitor & Indutor
Indutor
Componente com 2 terminais que armazena energia em
um campo magnético
Consiste de um condutor (fio) enrolado em forma de
espiras
Símbolos
– Fixo, núcleo de ar Fixo, núcleo de ferro
Não dissipa energia (como os resistores)
– Energia é armazenada em campo magnético
Unidade de Indutância: Henry [H], pelo cientista
americano Joseph Henry
Valor da indutância
– Indicado no corpo do componente, com números impressos
7
8
Variável
Capacitor & Indutor
Análise em Corrente Contínua
Capacitor em Circuito CC
Indutor
Relação Tensão/Corrente em um indutor
Carga do Capacitor
ͳǤ
ோ ʹǤ
– ௧ τ τ
͵Ǥ
Associação de indutores
ͶǤ
1 ିೃ ͷǤ
ିೃ
– ௗ ௧
ௗ௧
» Em regime, a tensão no indutor é nula se a corrente é constante
ଵ
௧
బ
ௗ௩ ௧
ௗ௧
– Série: ଵ ଶ ⋯
– Paralelo:
ଵ
ଵ
భ
ଵ
మ
⋯
ଵ
ா
ோ
9
Análise em Corrente Contínua
Capacitor em Circuito CC
Descarga do Capacitor
ͳǤ
0 ோ ʹǤ
0 ͵Ǥ
0 ௗ௩ ௧
ௗ௧
10
Análise em Corrente Contínua
Capacitor em Circuito CC
Mudando a chave
rapidamente
– Carga e descarga se
alternam
ͶǤ
ͷǤ
ିೃ
௩ ሺ௧ ሻ
బ ோ
Alterando R e C
αͲǡͷ
– Tempo de carga (e de
descarga) mudam
ିೃ
αͳ
αʹ
αͷ
11
12
Análise em Corrente Contínua
Capacitor em Circuito CC
Constante de Tempo: τ – Determina os
tempos de carga e
descarga do
capacitor
Análise em Corrente Contínua
Indutor em Circuito CC
Carga do Indutor
ͳǤ
ோ ʹǤ
1 ି ಽ ௧ ͵Ǥ
ି ಽ ௧
ೃ
ா
ோ
ೃ
– Para efeitos
práticos, carga (ou
descarga) completa
com 5τ
– Unidade: segundo
[s]
ͳǤ
0 ோ ʹǤ
ି ಽ ௧
͵Ǥ
ି ಽ ௧
ா
ோ
ೃ
ೃ
13
Análise em Corrente Contínua
Indutor em Circuito CC
Constante de Tempo: τ Descarga do Indutor
ࡸ
ࡾ
– Determina os
tempos de carga e
descarga do
capacitor
14
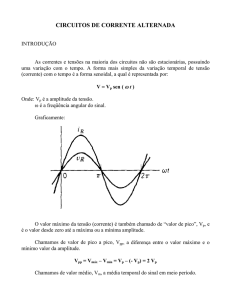
Análise em Corrente Alternada
Resistor em Circuito CA
Análise do Circuito
– Fonte de tensão
sinω
– Tensão no resistor
sinω
– Corrente no resistor
– Para efeitos
práticos, carga (ou
descarga) completa
com 5τ
sinω
– Corrente e tensão em fase
– Potência sempre positiva
– Unidade: segundo
[s]
15
16
Análise em Corrente Alternada
Capacitor em Circuito CA
Análise do Circuito
Análise em Corrente Alternada
Capacitor em Circuito CA
Representação Vetorial
– Fonte de tensão
Reatância
sinω
– Corrente no resistor
– Tensão no capacitor
sinω
– Corrente no capacitor
E
sinω
R
– Corrente no capacitor
ω cos ω
π
ωsin ω 2
ωsin ω – Corrente adiantada relação à
tensão em 90°
– Potência positiva (carga) e
negativa (descarga)
– Portanto,
ଵ
ω
π
2
é equivalente a – Reatância Capacitiva: 17
Análise em Corrente Alternada
Indutor em Circuito CA
18
Análise em Corrente Alternada
Indutor em Circuito CA
Representação Vetorial
Análise do Circuito
– Fonte de tensão
Reatância
sinω
– Corrente no resistor
– Tensão no indutor
sinω
– Corrente no capacitor
1
cos ω
ω
π
sin ω ω
2
– Corrente atrasada relação à
tensão em 90°
– Potência positiva (carga) e
negativa (descarga)
ଵ
ω
– Reatância varia inversamente com frequência
19
E
sinω
R
– Corrente no indutor
π
sin ω ω
2
– Portanto, ω é equivalente a – Reatância Indutiva: ω
– Reatância varia diretamente com frequência
20
Análise em Corrente Alternada
Impedância Elétrica (ࢆ)
Análise em Corrente Alternada
Impedância Elétrica (ࢆ)
É a oposição que o circuito faz a passagem da corrente
elétrica
Estende o conceito de resistência elétrica a circuitos CA
Possui magnitude (módulo) e fase (argumento)
Representações
– Cartesiana: – Polar: θ
É representada como um número complexo: – Parte real é a resistência Associação Série
ଵ ଶ ⋯
– Parte imaginária é a reatância » Reatância indutiva, quando parte imaginária é positiva: 0
» Reatância capacitiva, quando parte imaginária é negativa: 0
Associação Paralelo
1
1
1
1
⋯
ଵ ଶ
21
22
Análise em Corrente Alternada
Circuito R-C Série
Circuito R-C Série (cont.)
Resposta com a Frequência
Análise do Circuito
– Se a frequência aumenta, a
reatância capacitiva diminui
– Fonte de tensão:
sin ω sin2π
V
– A frequência não altera o
valor da resistência
– Impedância:
» Associação série de 2 impedâncias
– Portanto, para ଵ
» Resistor: » Capacitor: Análise em Corrente Alternada
ω
» Impedância equivalente: » Módulo da impedância: » Argumento da impedância: arg arctan
23
ω
మ
భ
ଷ
» o módulo da impedância
equivalente diminui | | | | | |
θ
ω ଶ
arctan ω » o argumento da impedância
equivalente fica menos
negativo
24
Análise em Corrente Alternada
Circuito R-C Série (cont.)
Resposta com a Frequência
– Filtro Passa-Baixa
Análise em Corrente Alternada
Circuito R-C Série (cont.)
Resposta com a Frequência
– Filtro Passa-Alta
25
Análise em Corrente Alternada
Circuito R-C Série (cont.)
Análise em Corrente Alternada
Circuito R-C Paralelo
Análise do Circuito
Exemplo
– Para 10 V, 60 Hz, 5Ω, e 100μF
ͳǤ 10sin120π
V, 10&0&
ʹǤ | | 26
π
π××
26,5Ω, 26,5∠ 90°Ω
͵Ǥ 5 26,5& 27& 79,3&&
ͶǤ 10∠0° - 27∠ 79.3° 0,37∠79,3°A 0,07 0,36 A
ͷǤ 5∠0° 0 0,37∠79,3° 1,85∠79,3° V
Ǥ 26,5& 90& 0 0,37∠79,3° 9,83∠ 10,7° V
– Fonte de tensão:
sin ω sin2π
V
– Impedância:
» Associação paralelo de 2 impedâncias
» Resistor: » Capacitor: ω
» Impedância equivalente: Ǥ 0,34 1,82 9,66 1,82 10 10&0& V
భ
మ
భమ
ω
θ
» Módulo da impedância: మమ
» Argumento da impedância: arg arctan
27
28
మ
భ
మ
ω
arctanω
Análise em Corrente Alternada
Circuito R-C Paralelo (cont.)
Exemplo
ͳǤ 10sin120π
V, 10&0& V
ʹǤ | | ͶǤ π
Circuito R-L Série
Análise do Circuito
– Para 10 V, 60 Hz, 5Ω, e 100μF
͵Ǥ Análise em Corrente Alternada
π××
,
26,5Ω, 26,5∠ 90°Ω
– Fonte de tensão:
sin ω sin2π
V
– Impedância:
» Associação série de 2 impedâncias
4,83 0,91& 4,91& 10,7&&
10∠0° - 4,91∠ 10,7° 2,04∠10,7°A 2 0,38 A
» Resistor: » Indutor: ω
» Impedância equivalente: ω θ
» Módulo da impedância: ͷǤ 10∠0° - 5∠0° 2∠0° A
Ǥ 10∠0° - 26,5∠ 90° 0,377∠90° A
Ǥ 2 0,377 2,04&10,7& A
» Argumento da impedância: arg arctan
29
Análise em Corrente Alternada
Circuito R-L Série (cont.)
Resposta com a Frequência
– Se a frequência aumenta, a
reatância indutiva aumenta
ଶ
మ
భ
arctan
ω
Análise em Corrente Alternada
Circuito R-L Série (cont.)
Resposta com a Frequência
– Filtro Passa-Baixa
- Filtro Passa-Alta
ଷ
» o módulo da impedância
equivalente aumenta
| | | |
» o argumento da impedância
equivalente fica mais positivo
31
ω
30
– A frequência não altera o
valor da resistência
– Portanto, para ଵ
32
Análise em Corrente Alternada
Circuito R-L Série (cont.)
Exemplo
ͳǤ 10sin120π
V, 10&0& V
ʹǤ | | 2π 2π 0 60 0 10m 3,77Ω, 3,77∠90°Ω
͵Ǥ 5 3,77& 6,26&37,0&&
ͶǤ Circuito R-L Paralelo
Análise do Circuito
– Para 10 V, 60 Hz, 5Ω, e 10 mH
Análise em Corrente Alternada
10∠0° - 6,26∠37,0° 1,60∠ 37,0°A 1,28 0,96 A
ͷǤ 5∠0° 0 1,60∠ 37,0° 7,98∠ 37,0° V
Ǥ 3,77&90& 0 1,60∠ 37,0° 6,02∠53,0° V
– Fonte de tensão:
sin ω sin2π
V
– Impedância:
» Associação série de 2 impedâncias
» Resistor: » Indutor: ω
» Impedância equivalente: భ
Ǥ 6,38 4,81 3,62 4,81 10 10&0& V
మ
భమ
మమ
» Argumento da impedância: arg arctan
33
Circuito R-L Paralelo (cont.)
మ
θ
మ
భ
ω మ
arctan
ω
34
Análise em Corrente Alternada
Circuito R-L-C Série
Análise do Circuito
Exemplo
– Para 10 V, 60 Hz, 5Ω, e 10 mH
ͳǤ 10sin120π
V, 10∠0° V
ʹǤ | | 2π 2π 0 60 0 10m 3,77Ω, 3,77∠90°Ω
͵Ǥ ω » Módulo da impedância: Análise em Corrente Alternada
,
3,01∠53,0°Ω
ͶǤ 10∠0° - 3,01∠53,0° 3,32∠ 53,0°A
ͷǤ 10∠0° - 5∠0° 2∠0° A
Ǥ 10∠0° - 3,77∠90,0° 2,65∠ 90,0° V
ಽ
– Fonte de tensão:
sin ω sin2π
V
– Impedância:
» Associação série de 3 impedâncias
» Resistor: » Indutor: ω
» Capacitor: ω » Impedância equivalente: Ǥ 2 2,65 3,32& 53,0& A
35
36
ω ω θ
Análise em Corrente Alternada
Circuito R-L-C Série (cont.)
Exemplo
– Para 120 V, 60 Hz, 250Ω, 650 mH, e 1,5μF
ͳǤ 120sin120π
V, 120∠0° V
ʹǤ | | 2π 2π 0 60 0 650m 245Ω
͵Ǥ | | π
1768Ω
π××,
ͶǤ 250 245 1768 250 1523& 1544& 80,7&Ω
ͷǤ 120∠0° - 1544∠ 80,7° 77,7∠80,7° mA
Ǥ 250∠0° 0 77,7m∠80,7° 19,4∠80,7° V
Ǥ 245&90& 0 77,7m∠80,7° 19,0∠170,7° V
ͺǤ 1768∠ 90° 0 77,7m∠80,7° 137,5∠ 9,3° V
ͻǤ 3,1 19,2 18,8 3,1 135,7 22,3 120&0&V
Transformador
Dispositivo que transfere energia elétrica entre 2
ou mais circuitos através de indução
eletromagnética
Compõe de 2 ou mais indutores (denominados
enrolamentos) acoplados magneticamente
A corrente por cada um dos enrolamentos altera o campo
magnético resultante influenciando a corrente induzida
nos outros enrolamentos
São usados para transformar tensão e corrente
alternadas, isto é, alterar valores de tensão e
corrente, mas mantendo a mesma potência
& & ou ' ( ' (
37
38
Transformador
Na maioria dos casos tem 2
enrolamentos denominados
de primário e secundário
Transformador
Análise
Relação de transformação é dada pela relação entre os
números de espiras de cada enrolamento
ು
ೄ
Enrolamento primário é
conectado à fonte de energia
– Relação de tensão:
Enrolamento secundário é
conectado à carga
– Relação de corrente:
ூು
ூೄ
ேು
ேೄ
ேೄ
ேು
– Balanço de potência: ) * )ௌ *ௌ
Símbolos
Núcleo de ar
Núcleo de Ferro
39
40