Tensões

Tensor tensão e vetor tensão
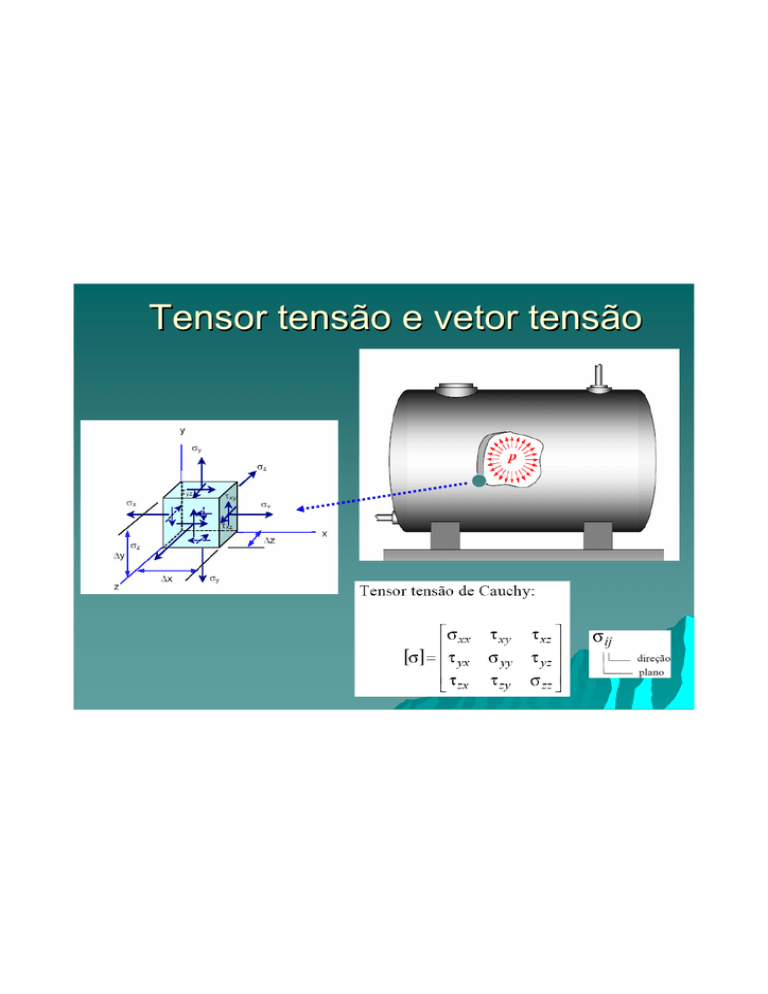
Tensor tensão e vetor tensão
y
C
dA
dA
Sy
y
n
θx
σx
τxz
x
z
τxy
τyz
A
z
σz
n
θx
τzx
Sx
τzy
Sz
τyx
x
B
σy
n = vetor unitário pertencente ao plano ABC
S (Sx, Sy, Sz) = vetor tensão no plano ABC
σx, σy, σz = componentes escalares de
tensão normal
vetor tensão:
r
r
S = σn
Estado de tensão num ponto
- designando por dA a área onde atua a tensão
desconhecida S (de componentes Sx, Sy, e Sz) e por l, m
e n os cossenos diretores do vetor unitário n, pode-se
demonstrar que:
σ x .l + τ yx .m + τ zx .n = S x
τ xy .l + σ y .m + τ zy .n = S y
τ xz .l + τ yz .m + σ z .n = S z
Estado de tensão num ponto
- ou, na forma matricial:
σ x τ yx

τ xy σ y
τ
 xz τ yz
τ zx  l  S x 
   
τ zy  m = S y 
 
σ z  n 
S 
z
Estado de tensão num ponto
• Tensão é uma grandeza tensorial: [σ] - chamado tensor
de tensões;
• Uma vez conhecidas as nove componentes do tensor de
tensões, pode-se determinar o vetor tensão atuando sobre
qualquer plano que passa pelo ponto;
• Pode-se mostrar que o tensor de tensões é simétrico, ou
seja, σxy = σyx,σxz = σzx e σyz = σzy . Logo, [σ] possui
apenas seis componentes independentes.
Estado uniaxial de tensão
Ex. – ensaio de tração
σ x
[σ ] =  0
 0
0 0
0 0

0 0
Estado plano de tensões
Ex. – peças de pequena espessura
σ x τ yx
[σ] = τ xy σ y

0 0
0

0
0
Estado triplo de tensões
σ x

[σ ] = τ xy
τ
 xz
τ yx
τ zx 
σy
τ zy 
τ yz

σ z 
Tensões principais e planos
principais
Dado o estado de tensão num ponto, os planos principais
são definidos como aqueles planos onde a componente
tangencial (cisalhante) do vetor tensão é nula.
Nestes planos, atuam as tensões principais (σp), as quais
correspondem às máximas tensões normais existentes.
Matematicamente, a solução do sistema a seguir permite
identificar tais tensões:
(σ x − σ p ) τ yx
τ zx 


 τ xy (σ y − σ p ) τ zy
 =0
 τ

(
)
τ
σ
σ
−
xz
yz
z
p 

Tensões principais e planos
principais
o que leva a uma equação do 3º grau em σp, cujas raízes
correspondem às tensões principais - σp1 > σp2 > σp3:
∴ σ p − I1.σ p + I2.σ p − I3 = 0
3
2
onde:
I1 = σ x + σ y + σ z
I2 = σ x .σ y + σ x .σ z + σ z .σ y − τ xy − τ xz − τ yz
2
2
2
I3 = σ x .σ y .σ z − σ x .τ yz − σ y .τ xz − σ z .τ xy + 2.τ xy .τ xz .τ yz
2
2
2
Exercicios – Tensões principais
Determine as tensões principais e os planos principais
correspondentes:
Exercicios – Tensões principais
Exercicios – Tensões principais
No ponto P do plano de uma dada seção transversal de
uma viga atuam as tensões: 40MPa (tração) e 48MPa (no
sentido oposto ao do eixo y).
Para tal ponto, pede-se determinar:
a) as tensões normal e tangencial em um plano
perpendicular ao plano xy, e cuja normal n forme com o
eixo x um ângulo de 30º como indicado;
b) as máximas tensões normais de tração e de compressão,
indicando a orientação dos planos onde ocorrem.
Exercicios – Tensões principais
Circulo de Mohr
Embora não seja mais usado como era até
algumas décadas atrás, o Círculo de Mohr constitui
uma maneira rápida e versátil de se analisar o
estado de tensões em um ponto.
Circulo de Mohr - Exemplos
Circulo de Mohr - Exemplos
Circulo de Mohr - Exemplos
Circulo de Mohr - Exemplos
Circulo de Mohr - Exemplos
Exercicios – Circulo de Mohr
Num certo ponto de uma viga são conhecidas as seguintes
tensões: σx = + 50MPa; σy = -10MPa; τxy = τyx = 40MPa.
Utilizando o Círculo de Mohr, pede-se determinar:
- as tensões principais;
- a máxima tensão tangencial
- a orientação dos planos principais.
Exercicios – Circulo de Mohr
Exercicios – Circulo de Mohr
São conhecidas as tensões atuantes no ponto K da viga
esquematizada. Utilizando o círculo de Mohr, determine
as tensões e as direções principais.
Exercicios – Circulo de Mohr