RECUPERAÇÃO FINAL / 2013 – MATEMÁTICA – prof. HAWLEY
1ª Série do Ensino Médio
LISTA DE EXERCÍCIOS
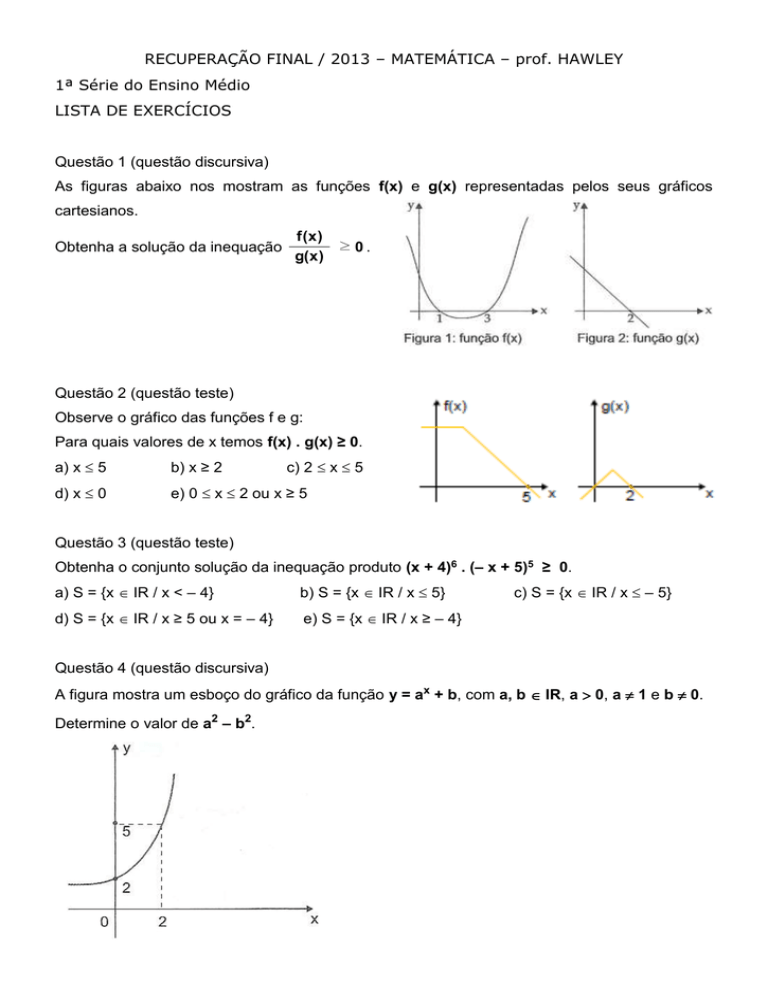
Questão 1 (questão discursiva)
As figuras abaixo nos mostram as funções f(x) e g(x) representadas pelos seus gráficos
cartesianos.
Obtenha a solução da inequação
f (x )
≥ 0.
g( x )
Questão 2 (questão teste)
Observe o gráfico das funções f e g:
Para quais valores de x temos f(x) . g(x) ≥ 0.
a) x 5
b) x ≥ 2
c) 2 x 5
d) x 0
e) 0 x 2 ou x ≥ 5
Questão 3 (questão teste)
Obtenha o conjunto solução da inequação produto (x + 4)6 . (– x + 5)5 ≥ 0.
a) S = {x IR / x < – 4}
b) S = {x IR / x 5}
d) S = {x IR / x ≥ 5 ou x = – 4}
e) S = {x IR / x ≥ – 4}
c) S = {x IR / x – 5}
Questão 4 (questão discursiva)
A figura mostra um esboço do gráfico da função y = ax + b, com a, b IR, a 0, a 1 e b 0.
Determine o valor de a2 – b2.
Questão 5 (questão teste)
A inflação anual de um país decresceu no período de sete anos. Esse fenômeno pode ser
representado por uma função exponencial do tipo f(x) = a . b x, conforme o gráfico abaixo.
Determine a taxa de inflação desse país no quarto ano de declínio.
a) 100%
b) 60%
c) 10%
d) 195%
e) 450%
Questão 6 (questão discursiva)
Resolver, no conjunto dos reais, a equação 3x + 1 – 3x = 3x – 2 + 51.
(não se esqueça de escrever como resposta o conjunto solução!)
Questão 7 (questão teste)
Qual o valor de x que torna verdadeira a equação 2x + 2x + 3 – 2x – 1 = 34?
a) x = 3
b) x = 2
c) x = 1
d) x = 0
e) x = – 1
Questão 8 (questão discursiva)
Resolver a inequação (0,3) 3x – 1 (0,09)5 no conjunto dos números reais.
(não se esqueça de escrever como resposta o conjunto solução!)
Questão 9 (questão discursiva)
Num filme de ficção cientifica, foi dito que o crescimento populacional de uma certa bactéria,
em condições experimentais e controladas, obedeceria à seguinte fórmula: f(t) = 1.000 2t,
sendo f(t) o número de bactérias e t o tempo (em horas).
a) Qual o número de bactérias no instante inicial do experimento?
b) Após 3 horas, qual será o número de bactérias?
Questão 10 (questão discursiva)
Calcule:
a)
b) 5 –
– 3 =
d) – 3,15 =
=
c) 2 –
=
e) – 3,14 =
Questão 11 (questão teste)
Um método para se estimar a ordem de grandeza de um número positivo N é usar uma
pequena variação do conceito de notação cientifica. O método consiste em determinar o valor x
que satisfaça a equação 10x = N e usar as propriedades dos logaritmos para saber o número
de casas decimais desse numeral.
= x bx = a, determine qual dos números abaixo
Usando a definição de logaritmo:
mais se aproxima de N = 2120 . 330 .
Dados log 2 = 0,30 e log 3 = 0,47.
a) 1050
b) 1045
c) 1055
d) 1060
e) 1065
Questão 12 (questão teste)
Usando as propriedades dos logaritmos determine o valor da soma:
.
a) – 1
b) – 2
c) 0
d) 2
e) 3
Questão 13 (questão teste)
Em Química, o pH é definido por: pH = – log [H+], em que [H+] é a concentração de hidrogênio,
em íons-grama, por litro de solução.
Para uma solução com [H+] = 1,0 . 10 – 8, obtenha o valor do pH.
a) – 8
b) 0,8
c) 8
d) 8 – 1
e) – 0,8
Questão 14
Num laboratório, foi feito um estudo sobre a evolução de uma população de vírus. Ao final de
um minuto do início das observações, existia 1 elemento na população; ao final de dois
minutos, existiam 5, e assim por diante. A seguinte sequência de figuras apresenta as
populações do vírus (representado por um círculo), ao final de cada um dos quatro primeiros
minutos.
Supondo que se manteve constante o ritmo de desenvolvimento da população, determine o
número de vírus no final de 1 hora.
a) 232
b) 241
c) 233
d) 237
e) 238
Questão 15
Em 5 de junho de 2004, foi inaugurada uma pizzaria que só abre aos sábados. No dia da
inauguração, a pizzaria recebeu 40 fregueses. A partir daí, o número de fregueses que passou
a frequentar a pizzaria cresceu em progressão aritmética de razão 6, até que atingiu a cota
máxima de 136 pessoas, a qual tem se mantido. Determine o número de sábados que se
passaram, excluindo-se o sábado da inauguração, para que a cota máxima de fregueses fosse
atingida pela primeira vez.
a) 26
b) 30
c) 20
d) 10
e) 16