Apostila1 de Introdução à Probabilidade e Variáveis Aleatórias

UNIVERSIDADE FEDERAL DE CAMPINA GRANDE
UNIDADE ACADÊMICA DE MATEMÁTICA E ESTATÍSTICA
Apostila1
de
Introdução à Probabilidade
e
Variáveis Aleatórias
Prof. Dr. Gilberto S. Matos
(http://sites.google.com/site/gilbertosmatos1)
Campina Grande - PB
Março / 2012
1
Esta apostila foi iniciada em 2002 através de notas de aula desenvolvidas pelos professores Alexsandro B. Cavalcanti e Gilberto S. Matos sob a assessoria do professor Francisco M. de Souza. Desde
então, vários professores da Área de Estatística da UAME/CCT/UFCG vêm gentilmente contribuindo
para o seu desenvolvimento.
2
Sumário
1 Probabilidade
7
1.1
Objetivo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7
1.2
Introdução . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7
1.3
Definições Básicas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
8
1.4
Abordagens para Definir Probabilidade . . . . . . . . . . . . . . . . . .
12
1.4.1
Pela Freqüência Relativa - (Lei dos Grandes Números) . . . . .
12
1.4.2
Definição Clássica de Probabilidade . . . . . . . . . . . . . . . .
13
1.4.3
Definição Axiomática de Probabilidade . . . . . . . . . . . . . .
18
1.5
Eventos Independentes . . . . . . . . . . . . . . . . . . . . . . . . . . .
19
1.6
Exercícios . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
20
1.7
Probabilidade Condicional . . . . . . . . . . . . . . . . . . . . . . . . .
22
1.7.1
Teorema do Produto . . . . . . . . . . . . . . . . . . . . . . . .
23
1.8
Eventos Independentes . . . . . . . . . . . . . . . . . . . . . . . . . . .
23
1.9
Teorema da Probabilidade Total . . . . . . . . . . . . . . . . . . . . . .
24
1.10 Teorema de Bayes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
24
1.11 Exercícios . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
26
2 Variáveis Aleatórias: Discretas e Contínuas
29
2.1
Introdução . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
29
2.2
Variáveis Aleatórias Discretas . . . . . . . . . . . . . . . . . . . . . . .
31
2.3
Variáveis Aleatórias Contínuas . . . . . . . . . . . . . . . . . . . . . . .
32
2.4
Função de Distribuição Acumulada . . . . . . . . . . . . . . . . . . . .
33
2.4.1
Propriedades da Função de Distribuição . . . . . . . . . . . . .
35
Exercícios . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
36
2.5
3 Caracterização Adicional das Variáveis Aleatórias
3
37
4
SUMÁRIO
3.1
Introdução . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
37
3.2
O Valor Esperado ou Esperança de Uma Variável Aleatória . . . . . . .
37
3.3
Esperança de uma Função de uma Variável Aleatória . . . . . . . . . .
39
3.4
Propriedades do valor esperado . . . . . . . . . . . . . . . . . . . . . .
40
3.5
A Variância de uma Variável Aleatória . . . . . . . . . . . . . . . . . .
41
3.6
Propriedades da variância . . . . . . . . . . . . . . . . . . . . . . . . .
42
3.7
Exercícios: Valor Esperado e Variância . . . . . . . . . . . . . . . . . .
43
4 Relação de Exercícios
47
5 Modelos Probabilísticos para Variáveis Aleatórias Discretas
49
5.1
Introdução . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
49
5.2
Distribuição de Bernoulli . . . . . . . . . . . . . . . . . . . . . . . . . .
49
5.3
Distribuição Binomial . . . . . . . . . . . . . . . . . . . . . . . . . . . .
50
5.4
Distribuição Hipergeométrica . . . . . . . . . . . . . . . . . . . . . . .
51
5.5
Distribuição de Poisson . . . . . . . . . . . . . . . . . . . . . . . . . . .
52
5.6
Exercícios: Modelos Probabilísticos Discretos . . . . . . . . . . . . . . .
54
6 Modelos Probabilísticos para Variáveis Aleatórias Contínuas
57
6.1
Distribuição Uniforme . . . . . . . . . . . . . . . . . . . . . . . . . . .
57
6.2
Distribuição Exponencial . . . . . . . . . . . . . . . . . . . . . . . . . .
58
6.3
Distribuição Normal (Gaussiana) . . . . . . . . . . . . . . . . . . . . .
59
6.3.1
Propriedades da Distribuição Normal . . . . . . . . . . . . . . .
60
6.3.2
Exemplos do Uso da Tabela Normal Padrão . . . . . . . . . . .
61
6.3.3
Aproximação da Binomial pela Normal . . . . . . . . . . . . . .
61
6.4
Exercícios: modelos de variáveis contínuas . . . . . . . . . . . . . . . .
64
6.5
Exercícios: Distribuição Normal . . . . . . . . . . . . . . . . . . . . . .
69
7 Variáveis Aleatórias Bidimensionais
73
7.1
Introdução . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
73
7.2
Variáveis Aleatórias Discretas . . . . . . . . . . . . . . . . . . . . . . .
73
7.2.1
Função de Probabilidade Conjunta . . . . . . . . . . . . . . . .
74
7.2.2
Distribuições Marginais de Probabilidades . . . . . . . . . . . .
76
7.2.3
Distribuição Condicional . . . . . . . . . . . . . . . . . . . . . .
76
7.2.4
Independência . . . . . . . . . . . . . . . . . . . . . . . . . . . .
77
SUMÁRIO
7.3
5
7.2.5
Função de Variáveis Aleatórias Discretas . . . . . . . . . . . . .
78
7.2.6
Esperança de uma função de duas variáveis aleatórias . . . . . .
79
7.2.7
Medida de Correlação entre duas Variáveis . . . . . . . . . . . .
79
7.2.8
Exercícios . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
82
Variáveis Aleatórias Contínuas . . . . . . . . . . . . . . . . . . . . . . .
84
7.3.1
Função Densidade Conjunta . . . . . . . . . . . . . . . . . . . .
84
7.3.2
Densidades Marginais . . . . . . . . . . . . . . . . . . . . . . . .
84
7.3.3
Independência . . . . . . . . . . . . . . . . . . . . . . . . . . . .
84
7.3.4
Distribuições Condicionais . . . . . . . . . . . . . . . . . . . . .
85
7.3.5
Função de Variáveis Aleatórias Contínuas . . . . . . . . . . . . .
85
7.3.6
Exercícios . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
86
8 Relação de Exercícios
89
I ANEXO
Tabelas
93
6
SUMÁRIO
Capítulo 1
Probabilidade
1.1
Objetivo
Definir modelos matemáticos probabilísticos que sejam convenientes para a descrição
e interpretação de fenômenos aleatórios.
1.2
Introdução
Ao jogarmos uma moeda para o ar, de modo geral, não podemos afirmar se ocorrerá
cara ou coroa. Da mesma forma, quando lançamos um dado não sabemos qual das
faces 1, 2, 3, 4, 5, ou 6 ocorrerá. No campo dos negócios e do governo há numerosos
exemplos de tais situações. Por exemplo, a incerteza existe quando desejamos realizar
uma previsão sobre a procura de um novo produto, a opinião pública em relação a
determinado assunto, o sucesso de um novo plano econômico, etc - tudo isso contém
algum elemento de acaso.
Na Estatística, a incerteza existe quando se quer fazer alguma afirmação a respeito de alguma característica populacional baseada em informações extraídas de dados
amostrais. Neste caso, a aplicação da Teoria das Probabilidades é de fundamental
importância para a solução de problemas de Inferência Estatística.
Independente de qual seja a aplicação em particular, a utilização das probabilidades indica que existe um elemento de acaso, ou de incerteza, quanto à ocorrência ou
não de um evento futuro. Assim é que em muitos casos, pode ser impossível afirmar
com antecipação o que ocorrerá. No entanto, é possível dizer o que pode ocorrer.
O ponto central em todas essas situações é a possibilidade de quantificar quão
provável é determinado evento.
Em suma, podemos dizer que, as probabilidades são utilizadas para exprimir a
chance de ocorrência de determinado evento.
7
8
CAPÍTULO 1. PROBABILIDADE
1.3
Definições Básicas
Definição 1.3.1 (Experimentos Aleatórios ou Fenômenos Aleatórios). são
aqueles onde o processo de experimentação está sujeito a influências de fatores casuais
e conduz a resultados incertos.
Notação: E.
Exemplos:
E1 : Jogar uma moeda e observar a face superior.
E2 : Lançar um dado e observar o número da face superior.
E3 : Numa linha de produção, conta-se o número de peças produzidas com defeito
em um dia.
E4 : Uma lâmpada é fabricada. Em seguida é testada a duração da vida útil dessa
lâmpada.
Observações:
a) Cada experimento poderá ser repetido um grande número de vezes sob as mesmas
condições;
b) Não podemos afirmar que resultado particular ocorrerá, porém podemos descrever o conjunto de todos os possíveis resultados do experimento;
c) Quando o experimento é repetido um grande número de vezes, surgirá uma regularidade nos resultados. Esta regularidade, chamada de regularidade estatística,
é que torna possível construir um modelo matemático preciso com o qual se analisará o experimento.
Definição 1.3.2 (Espaço Amostral). é o conjunto de todos os possíveis resultados
de um experimento aleatório.
Notação: S ou Ω.
Exemplos:
Os espaços amostrais associados aos experimentos aleatórios E1 , E2 , E3 e E4 são:
S1 =
S2 =
S3 =
S4 =
1.3. DEFINIÇÕES BÁSICAS
9
Definição 1.3.3 (Evento). Dado um espaço amostral S associado a um experimento
E, definimos como evento, qualquer subconjunto desse espaço amostral, ou seja, é
qualquer coleção de resultados do experimento E.
Notação: A, B, C, D, etc.
Exemplos:
1 - Considerando o espaço amostral S2 , exemplos de eventos seriam:
A: Ocorre face par =
B: Ocorre um número menor que 4 =
C: Ocorre um número maior que 0 =
D: Ocorre o número 10 =
2 - Considerando o espaço amostral S3 , um exemplo de evento seria:
A: A vida útil de uma lâmpada é menor que 10 horas =
Observações:
i) Dizemos que um evento A ocorre se o resultado do experimento, s ∈ S, pertencer
ao evento, ou seja, s ∈ A. Caso contrário, dizemos que o evento A não ocorre.
ii) Como os eventos de um espaço amostral são conjuntos, todas as operações da teoria dos conjuntos são válidas para obter novos eventos. Considere, por exemplo,
dois eventos A e B, então o evento:
a) A∪B ocorrerá se, e somente se, A ocorrer, ou B ocorrer, ou ambos ocorrerem;
b) A ∩ B ocorrerá se, e somente se, A e B ocorrerem simultaneamente;
c) A ocorrerá se, e somente se, A não ocorrer;
Um recurso gráfico, conhecido como Diagrama de Venn, poderá ser vantajosamente
empregado quando estivermos combinando conjuntos. Para ilustrar, vejamos como fica
este diagrama representando os eventos descritos nos itens a, b e c:
(Desenhar os Diagramas de Venn, para cada evento)
10
CAPÍTULO 1. PROBABILIDADE
Definição 1.3.4 (Eventos Mutuamente Excludentes). Dois eventos, A e B, são
denominados, mutuamente excludentes, se eles não puderem ocorrer simultaneamente,
ou seja, A ∩ B = φ.
Exercício: Esboce um Diagrama de Venn, representando dois eventos mutuamente
excludentes.
Exemplo 1.3.1. Ao lançar um dado e observar o número da face superior temos que
o evento A: observar face par é mutuamente excludente do evento B: observar face
ímpar, pois é impossível observar a ocorrência simultânea destes dois eventos, ou seja,
A ∩ B = φ.
Observação: Leis de D’Morgan
(i) A ∪ B = A ∩ B
(ii) A ∩ B = A ∪ B
Exemplos:
1 - Lança-se um dado e observa-se o número da face superior. Considerando este
experimento aleatório E e eventos associados ao espaço amostral S =
determine em notação de conjuntos os seguintes eventos:
a) A: Ocorre face par =
b) B: Ocorre um número menor que 4 =
c) C: ocorre face menor que 7 =
d) D: ocorre face cujo valor é maior que 6 =
e) A ∪ B
f) A ∩ B
g) A
h) B
i) A ∪ B
j) A ∩ B
k) A ∪ B
l) A ∩ B
,
1.3. DEFINIÇÕES BÁSICAS
11
m) A − B = A ∩ B
n) B − A = B ∩ A
15 - Sejam A e B dois eventos. Expresse as sentenças a seguir em termos de operações
entre eventos:
a) A e B ocorrem simultaneamente;
b) Pelo menos um dos eventos ocorre;
c) Nenhum dos eventos ocorre;
d) Apenas A ocorre;
e) Apenas B ocorre;
f) Exatamente um dos eventos ocorre.
12
CAPÍTULO 1. PROBABILIDADE
1.4
1.4.1
Abordagens para Definir Probabilidade
Pela Freqüência Relativa - (Lei dos Grandes Números)
Definição 1.4.1 (Freqüência Relativa). Suponha que um experimento é repetido n
vezes, e seja A e B dois eventos associados ao experimento. Sejam nA e nB o número
de vezes que o evento A e o evento B ocorram nas n repetições. A freqüência relativa
do evento A, representada por fA , é definida como
nA
fA =
.
n
Propriedades:
(i) 0 ≤ fA ≤ 1;
(ii) fA = 1, se, e somente se, A ocorrer em todas as n repetições;
(iii) fA = 0, se, e somente se, A nunca ocorrer nas n repetições;
(iv) Se A e B forem eventos mutuamente excludentes, e se fA∪B for a freqüência
relativa associada ao evento A ∪ B, então,
fA∪B = fA + fB .
Teorema 1.4.1 (Lei dos Grandes Números). Ao repetir um experimento um grande
número de vezes, a probabilidade de um evento A é aproximada pela freqüência relativa,
isto é,
nA
, quando n → ∞.
P (A) ∼
= fA =
n
Observação: Esta aproximação será tanto melhor quanto maior for o número
de repetições do experimento.
Exemplos:
1 - Ao lançar uma moeda honesta 5 vezes, ocorreram 4 caras. Baseado neste resultado, qual a probabilidade (aproximada) do evento A : ocorrer cara?
2 - Considere as seguintes situações:
(i) Numa pesquisa de mercado, 5 pessoas foram entrevistadas das quais 4
disseram que comprariam um novo produto a ser lançado.
(ii) Numa outra pesquisa de mercado, 300 pessoas foram entrevistadas das
quais 140 disseram que comprariam um novo produto a ser lançado.
a) Para cada pesquisa, determine a probabilidade de que uma pessoa qualquer
compre o novo produto.
b) Em qual das duas probabilidades estimadas você confia mais?
1.4. ABORDAGENS PARA DEFINIR PROBABILIDADE
1.4.2
13
Definição Clássica de Probabilidade
Definição 1.4.2 (Evento Simples e Evento Composto). Cada um dos possíveis
resultados que compõe o espaço amostral s1 , s2 , s3 , . . . é um evento simples, enquanto
um evento composto, A, é uma coleção de eventos simples.
Exemplo 1.4.1. Ao lançar um dado, os eventos simples serão: {1}, {2}, {3}, {4}, {5}
e {6} e um evento composto seria A : número par = {2, 4, 6}.
Definição 1.4.3 (Definição Clássica de Probabilidade). Suponha que um experimento tenha n eventos simples diferentes, cada um dos quais pode ocorrer com a
mesma chance. Se r eventos simples são favoráveis à ocorrência do evento A, então
Número de eventos simples favoráveis à ocorrência do evento A
#A
r
P (A) =
=
= .
Número total de resultados possíveis
#S
n
Observações:
(1) Nesta definição é fundamental que os eventos simples sejam igualmente prováveis, e, neste caso, é evidente que:
(i) P (e1 ) = P (e2 ) = ... = P (en ) = n1 , e
(ii) P (e1 ) + P (e2 ) + ... + P (en ) =
1
n
+
1
n
+ ... +
1
n
= n. n1 = 1.
(2) Espaços amostrais com as características acima descritas são conhecidos como
Espaços Amostrais Finitos e Equiprováveis.
(3) O evento S é denominado evento certo pois P (S) =
#S
= 1.
#S
(4) O evento φ é denominado evento impossível pois P (φ) =
#φ
0
=
= 0.
#S
#S
Exemplos:
1 - Considere o experimento E: lançar um dado equilibrado e observar o número da
face superior. Considere também, os seguintes eventos:
. A: Ocorre face par =
. B: Ocorre um número menor que 4 =
. C: ocorre face menor que 7 =
. D: ocorre face cujo valor é maior que 6 =
. A∩B =
. A∪B =
. B=
Determine a probabilidade de ocorrência de cada um dos eventos acima definidos.
14
CAPÍTULO 1. PROBABILIDADE
Noções Básicas de Técnicas de Contagem
Nem sempre a tarefa de calcular a probabilidade de um evento aleatório, da forma
P (A) = r/n, é simples. Em algumas situações é necessário alguns procedimentos
sistemáticos de contagem ou enumeração para se obter o número de maneiras, r, pelas
quais A pode ocorrer, bem como o número total de maneiras, n, pelas quais o espaço
amostral S pode ocorrer.
É no contexto descrito acima, que as técnicas de contagem são de fundamental
importância. Neste curso, veremos apenas alguns dos principais procedimentos de
contagem.
Princípio Fundamental da Contagem (P.F.C.) - Regra da Multiplicação
Suponha que um experimento possa ser realizado em k etapas, de modo que, para
a primeira etapa existem n1 resultados possíveis, para a segunda etapa n2 resultados
possíveis, e assim sucessivamente, até que para a k −ésima etapa existem nk resultados
possíveis. Então, existe um total de
n1 × n2 × .... × nk
resultados possíveis para este experimento.
Exemplos:
1 - Ao lançar um dado e uma moeda, quantos resultados possíveis podem ser obtidos?
Resp.: 12
2 - Uma companhia produz fechaduras que usam segredos numéricos para serem
abertas. Se cada segredo consiste de três números(dígitos) distintos, escolhidos
dentre os inteiros de 0 a 9, quantos segredos diferentes poderão ser fabricados?
a) Considerando a possibilidade de repetir os dígitos? E sem permitir a repetição de dígitos?
b) Sendo número par?
c) Sendo número par e divisível por 5?
3 - Quantos números naturais de 4 algarismos podem ser formados usando-se apenas
os algorismos 2, 3, 4 e 5, de forma que sejam menores do que 5000 e divisíveis
por 5? Resp.: 48
1.4. ABORDAGENS PARA DEFINIR PROBABILIDADE
15
Permutação
Dizemos que permutações de n elementos distintos são as sequências formadas com
todos os n elementos e que se destinguem umas das outras pela ordem de seus elementos. Assim, permutar os n objetos equivale a colocá-los dentro de uma caixa com n
compartimentos, em alguma ordenação.
Notação: Pnn ou, simplesmente, Pn .
Assim, aplicando a regra da multiplicação, temos que n elementos distintos podem
ser distribuídos em n caixinhas de n × (n − 1) × (n − 2) × · · · × 3 × 2 × 1 maneiras e,
portanto
Pn = n × (n − 1) × (n − 2) × · · · × 3 × 2 × 1.
Definição 1.4.4 (Fatorial). Sendo n um inteiro positivo, definimos n! = n(n−1)(n−
2) · · · 3.2.1 e o denominamos de fatorial de n. Também definimos 0! = 1.
Desta maneira, temos que:
Pn = n!
Arranjo
Dado um conjunto de n elementos, chama-se de arranjo simples dos n elementos tomados k a k (0 ≤ k ≤ n) a toda sequência de k elementos distintos do conjunto, que se
destingue das demais pela ordem dos seus elementos. Assim, arranjar n objetos equivale a colocá-los dentro de uma caixa com n compartimentos, em alguma ordenação,
um em cada compartimento, até que o k-ésimo compartimento seja preenchido.
Notação: Ank .
Desta forma, aplicando-se a regra da multiplicação, temos que:
Ank = n(n − 1)(n − 2) · · · (n − (k − 1)).
= n(n − 1)(n − 2) · · · (n − k + 1).
Agora, note que:
Ank = n(n − 1)(n − 2) · · · (n − k + 1)
(n − k)!
(n − k)!
E, portanto
Ank =
n!
.
(n − k)!
Observação: Note que, se k = n, temos
n!
n!
Ann =
=
= n! = Pn ,
(n − n)!
0!
ou seja, permutação é caso particular de arranjo (quando k = n).
16
CAPÍTULO 1. PROBABILIDADE
Exemplo 1.4.2. De um baralho com 52 cartas, 3 cartas são retiradas sucessivamente
e sem reposição. Quantas sequências de cartas são possíveis de se obter?
Exemplo 1.4.3. De quantas maneiras podemos dispor 8 pessoas em um banco com 8
lugares?
Exemplo 1.4.4. Quantos são os anagramas da palapra ALUNO?
Combinação
Quando uma amostra de k elementos for retirada (sem importar a ordem entre si) de
um conjunto
den elementos. O número de diferentes amostras possíveis é denotado
n
por Ckn =
e é igual a:
k
n!
n
=
k
k!(n − k)!
onde o símbolo ! significa que:
n! = n(n − 1)(n − 2)(n − 3) . . . (3)(2)(1)
Por exemplo, 5! = 5.4.3.2.1 [Nota: A quantidade 0! é definida como sendo igual a
1.]
Dedução da fórmula da combinação
Observe que Ank leva em consideração um experimento em que a ordem em que k
elementos são escolhidos dentre n é importante. Deste modo, podemos imaginar que
um experimento com estas características pode ser pensado como ocorrendo em duas
etapas (lembre-se do P.F.C.), de maneira que:
1 - Na 1a Etapa escolhemos k elementos dentre n sem nos preocuparmos com a ordem
de tais elementos (Ckn possibilidades), e
2 - Na 2a Etapa passamos a nos preocupar com o número de possibilidades que existe
para ordenar os k elementos (permutação dos k elementos = k!).
Desta forma temos que:
Ank = Ckn × k!
E, portanto,
Ckn
=
n
k
=
Ank
n!
=
.
k!
k!(n − k)!
1.4. ABORDAGENS PARA DEFINIR PROBABILIDADE
17
Exemplos:
1 - Qual é o número de possíveis empreendimentos quando desejamos selecionar dois
dentre quatro? Resp: 6
2 - Suponha que num lote com 20 peças existem cinco defeituosas. Escolhemos 4
peças do lote ao acaso, ou seja, uma amostra de 4 elementos, de modo que a
ordem dos elementos seja irrelevante:
a - Quantas amostras possíveis existem? Resp: 4845
b - Dentre todos os possíveis resultados, quantos levam à escolha de duas peças
defeituosas? Resp.: 1050
c - Qual é a probabilidade de sair duas peças defeituosas? Resp.: 0,217
18
CAPÍTULO 1. PROBABILIDADE
1.4.3
Definição Axiomática de Probabilidade
Definição 1.4.5 (Definição Axiomática de Probabilidade). Dado um espaço
amostral S, a probabilidade de um evento A ocorrer, representado por P (A) , é uma
função definida em S, que associa a cada evento A um número real, satisfazendo os
seguintes axiomas:
(A1) 0 ≤ P (A) ≤ 1;
(A2) P (S) = 1;
(A3) Se A e B forem mutuamente excludentes (A ∩ B = φ), então
P (A ∪ B) = P (A) + P (B) .
Observação: A probabilidade de um evento A, denotada por P (A) , indica a
chance de ocorrência do evento A. Quanto mais próxima de 1 é P (A), maior é a
chance de ocorrência do evento A, e quanto mais próxima de zero, menor é a chance
de ocorrência do evento A.
Principais Teoremas (Propriedades):
T1. Se φ denota o conjunto vazio (Evento Impossível), então
P (φ) = 0.
T2. Se A é o evento complementar de A, então
P (A) = 1 − P (A) .
T3. Se A e B são dois eventos quaisquer, então
P (A ∪ B) = P (A) + P (B) − P (A ∩ B) .
Exercício: Utilizando conhecimentos da teoria dos conjuntos e os axiomas A1,
A2 e/ou A3, demonstre os três (3) Teoremas ou Propriedades acima.
Exemplo 1.4.5. Considere um experimento aleatório com espaço amostral S e os
eventos A e B associados tais que: P (A) = 1/2, P (B) = 1/3 e P (A ∩ B) = 1/4.
Determine:
a) P (A)
b) P (B)
c) P (A ∪ B)
d) P (A ∩ B)
e) P (A ∪ B)
1.5. EVENTOS INDEPENDENTES
1.5
19
Eventos Independentes
A probabilidade da ocorrência de dois eventos simultaneamente, P (A∩B), depende
da natureza dos eventos, ou seja, se eles são independentes ou não.
Dois ou mais eventos são independentes quando a ocorrência ou não-ocorrência de
um não influencia a ocorrência do(s) outro(s).
Definição 1.5.1 (Eventos Independentes). Dois eventos A e B são independentes
se, e somente se
P (A ∩ B) = P (A)P (B).
Exemplo 1.5.1. Se duas moedas equilibradas (sem vício) são lançadas, determine
qual a probabilidade de ambas darem cara? E se três moedas fossem lançadas, qual a
probabilidade de ocorrer três caras?
Exemplo 1.5.2. Uma urna contém duas bolas brancas e cinco pretas. Qual a probabilidade de sair duas bolas pretas se os sorteios são feitos com reposição?
Exemplo 1.5.3. A probabilidade de que A resolva um problema é de 2/3, e a probabiliddae de que B o resolva é de 3/4. Se ambos tentarem independentemente, qual a
probabilidade de:
a) Ambos resolverem o problema?
b) O problema ser resolvido?
20
1.6
CAPÍTULO 1. PROBABILIDADE
Exercícios
1 - De uma linha de produção são retirados três (3) artigos e cada um é classificado
como bom (B) ou defeituoso (D). Determine o espaço amostral deste experimento
aleatório e expresse também o evento A: obter dois artigos defeituosos.
2 - Pedro tem dois automóveis velhos. Se nas manhãs frias, há 20% de probabilidade
de um deles não funcionar e 30% de outro não funcionar,
a) qual a probabilidade de nenhum funcionar?
b) qual a probabilidade dos dois funcionarem?
c) qual a probabilidade de pelo menos um funcionar?
d) qual a probabilidade de exatamente um funcionar?
3 - Considere o lançamento de dois dados equilibrados com o interesse de observar o
número das faces superiores.
a) Calcule a probabilidade dos eventos:
i) A: sair face par nos dois dados
ii) B: sair face par no primeiro dado
iii) C: sair face par no segundo dado
d) Os eventos B e C são independentes?
4 - De 120 estudantes, 60 estudam Francês, 50 Espanhol e 20 estudam Francês e
Espanhol. Se um estudante é escolhido ao acaso, encontre a probabilidade de
que ele:
a) estude Francês e Espanhol?
b) estude pelo menos uma das línguas?
c) não estude nem Francês nem Espanhol?
5 - Ao escolher entre diversos fornecedores de computadores, um comprador deseja
saber a probabilidade de um computador falhar durantes os dois primeiros anos.
Sabendo-se que só existem duas possibilidades; ou o computador falha durante
os dois primeiros anos ou não falha, qual é essa probabilidade? Agora se você
conhecesse o resultado de uma pesquisa do PC World feita com 4000 usuários
de computadores, na qual revela que 992 computadores falham durantes os dois
primeiros anos, qual será a probabilidade estimada? Resp.: 0,5 e 0,248.
6 - Um terço dos eleitores de certa comunidade é constituido de mulheres, e 40% dos
eleitores votaram na última eleição presidencial. Supondo que esses dois eventos
sejam independentes, determine a probabilidade de escolher um eleitor da lista
geral, que seja mulher e que tenha votado na última eleição presidencial.
7 - Uma urna contém duas bolas brancas e cinco pretas. Qual a probabilidade de
sair duas bolas pretas supondo que os sorteios são feitos com reposição?
1.6. EXERCÍCIOS
21
8 - Se cada carta de um baralho de 52 cartas tem a mesma chance de ser escolhida,
então qual é a probabilidade de:
a) se extrair cada uma delas?
b) de se extrair uma dama?
9 - Qual a probabilidade de se obter três ou menos pontos no lançamento de um
dado?
10 - Uma urna contém duas bolas brancas, três pretas e cinco azuis.
a) Qual a probabilidade de se extrair uma bola branca?
b) Qual a probabilidade de se extrair uma bola preta ou uma azul?
11 - No lançamento de dois dados qual a probabilidade de sair o par (5,2)?
22
CAPÍTULO 1. PROBABILIDADE
1.7
Probabilidade Condicional
Em algumas situações, a probabilidade de ocorrência de um certo evento pode ser
afetada se tivermos alguma informação sobre a ocorrência ou não de um outro evento.
Considere, por exemplo, o seguinte experimento:
E : Lançar um dado.
Seja o evento A: sair o no 3 =
Então, P (A) =
Considere, agora, o seguinte evento:
B: sair um número ímpar =
Logo, P (B) =
Suponha, agora, que soubéssemos da ocorrência de B e que quiséssemos calcular
a probabilidade de A. Iremos denotar essa probabilidade como P (A | B). Assim,
P (A | B) =
Formalmente definimos probabilidade condicional da maneira a seguir.
Definição 1.7.1 (Probabilidade Condicional). Dados dois eventos, A e B, denotaremos P (A | B) a probabilidade condicionada do evento A, quando B tiver ocorrido,
por:
P (A ∩ B)
P (A | B) =
P (B)
com P (B) 6= 0.
Exemplo 1.7.1. Dois dados são lançados e os seguintes eventos são considerados:
A = {(x1 , x2 ); x1 + x2 = 10}, e
B = {(x1 , x2 ); x1 > x2 }.
Baseado nestas informações, obtenha as seguintes probabilidades:
a) P (A)
c) P (A ∩ B)
b) P (B)
d) P (A | B)
e) P (B | A)
Observação: observe no exemplo acima que calcular probabilidade condicional
é equivalente à calcular a probabilidade do evento de interesse sob um novo espaço
amostral o qual é restrito de acordo com a informação fornecida. Caso não visualize
isto, descreva o conjunto(evento) dito conhecido e depois calcule a probabilidade do
evento de interesse sob este novo conjunto(espaço amostral).
1.8. EVENTOS INDEPENDENTES
1.7.1
23
Teorema do Produto
A partir da definição de probabilidade condicional, poderemos enunciar o teorema
do produto:
Teorema 1.2 (Teorema do Produto)
P (A ∩ B)
⇒ P (A ∩ B) = P (B)P (A | B).
P (B)
Analogamente,
P (A | B) =
P (B | A) =
P (A ∩ B)
⇒ P (A ∩ B) = P (A)P (B | A).
P (A)
Exemplos:
1 - Em um lote de 12 peças, 4 são defeituosas. Se duas peças são retiradas uma após
a outra sem reposição, qual a probabilidade de que:
a) ambas sejam boas?
b) ambas sejam defeituosas?
c) pelo menos uma seja defeituosa?
2 - Uma urna contém duas bolas brancas, três vermelhas e cinco azuis. Qual a probabilidade de se retirar sem reposição uma bola azul, uma branca e uma vermelha
exatamente nessa ordem?
1.8
Eventos Independentes
Um evento A é considerado independente de um outro evento B se a probabilidade
condicional de A dado B é igual a probabilidade de A, isto é, se
P (A | B) = P (A).
É evidente que se A é independente de B, então B é independente de A. Assim,
P (B | A) = P (B).
Logo, considerando o Teorema do Produto, observamos que a probabilidade da
ocorrência de dois eventos simultaneamente, P (A ∩ B), depende da natureza dos eventos, ou seja, se eles são independentes ou não e, no caso dos eventos serem independentes, já sabemos que
P (A ∩ B) = P (A)P (B).
Observação: A recíproca é verdadeira, isto é, se P (A ∩ B) = P (A)P (B), então
A e B são eventos independentes.
24
CAPÍTULO 1. PROBABILIDADE
Exercício
1 - Demonstre o que está sendo afirmado nesta seção, ou seja, que:
P (A ∩ B) = P (A)P (B) se, e somente se A e B são independentes.
1.9
Teorema da Probabilidade Total
Definição 1.9.1 (Partição do Espaço Amostral). Dizemos que os eventos B1 , B2 , ..., Bk
representam uma partição do espaço amostral S, quando
a) Bi ∩ Bj = φ, para todo i 6= j,
b) ∪ki=1 Bi = S,
c) P (Bi ) > 0, para todo i.
Considere, agora, um evento A referente a S, e B1 , B2 , ..., Bk uma partição de S.
Assim, podemos escrever
A = (A ∩ B1 ) ∪ (A ∩ B2 ) ∪ (A ∩ B3 ) ∪ ... ∪ (A ∩ Bk ).
Logo,
P (A) = P (A ∩ B1 ) + P (A ∩ B2 ) + P (A ∩ B3 ) + ... + P (A ∩ Bk ).
Então, como P (A ∩ Bj ) = P (Bj )P (A | Bj ), obteremos o que se denomina o
Teorema da Probabilidade Total:
P (A) = P (B1 )P (A | B1 ) + P (B2 )P (A | B2 ) + ... + P (Bk )P (A | Bk ).
1.10
Teorema de Bayes
Sob as mesmas hipóteses do teorema da probabilidade total, podemos calcular a
probabilidade de Bi dada a ocorrência de A da seguinte forma
P (Bi | A) =
P (Bi )P (A | Bi )
P (Bi ∩ A)
=P
.
P (A)
j P (Bj )P (A | Bj )
Este resultado é o que chamamos de Teorema de Bayes. Esse teorema é útil
0
quando conhecemos as probabilidades dos Bi s e a probabilidade condicional de A dado
Bi , mas não conhecemos diretamente a probabilidade de A.
Exemplos:
1.10. TEOREMA DE BAYES
25
1 - A proporção de peças produzidas pelas máquinas I, II e III é 30%, 30% e 40%,
respectivamente. Dentre estas peças, 4%, 3% e 2%, respectivamente, são defeituosas. Uma peça escolhida aleatoriamente, foi testada e verificou-se ser defeituosa. Qual é a probabilidade de que a peça tenha sido produzida pela máquina I?
E pela máquina II? E pela III?
2 - Suponha três urnas com as seguintes configurações: a urna 1 contém 3 bolas
pretas, 1 branca e 5 vermelhas; a urna 2 contém 4 bolas pretas, 3 brancas e 2
vermelhas; a urna 3 contém 2 bolas pretas, três brancas e 3 vermelhas. Escolheuse uma urna ao acaso e dela extraiu-se uma bola ao acaso, verificou-se que a bola
é branca. Qual a probabilidade da bola ter vindo da urna 1, 2? E da 3?
26
1.11
CAPÍTULO 1. PROBABILIDADE
Exercícios
1 - Suponha que a probabilidade de que ambas crianças gêmeas sejam meninos é 0,30
e que a probabilidade de que sejam meninas é 0,26. Dado que a probabilidade
de uma criança seja menino é 0.52, qual é a probabilidade de que:
a) A segunda criança seja um menino, sabendo-se que o primeiro é um menino?
Resp.: 0,577.
b) A segunda criança seja uma menina, sabendo-se que a primeira é uma menina? Resp.: 0,542.
2 - Uma urna contém duas bolas brancas, três verdes e cinco azuis. Se três bolas são
retiradas ao acaso, sem reposição, determine a probabilidade de:
a) três bolas verdes ocorrerem. Resp.: 0,0083.
b) exatamente uma bola verde ocorrer.Resp.: 0,175.
3 - A probabilidade de que um time de futebol vença seu próximo oponente é estimada em 0,7 se não chover, mas só em 0,5 se chover. Se os registros meteorológicos
mostrarem que choveu 40 por cento das vezes, na data do jogo, nos anos passados,
qual a probabilidade de que o time vença seu próximo oponente? Resp.: 0,62.
4 - Suponhamos que seja de 0,005 a probabilidade de que o motor de um monomotor
de combate falhe na decolagem e que a taxa de falha técnica do motor de um
bimotor de combate seja de 0,003. Se o bimotor não puder decolar a não ser que
ambos os motores estejam operando adequadamente, que avião é mais seguro na
decolagem? Resp.: P (bimotor falhar na decolagem) = 0, 006.
5 - Empregados de certa firma são submetidos a um teste de aptidão quando empregados pela primeira vez. A experiência mostrou que dos 60 por cento que
passaram no teste, 80 por cento deles eram bons trabalhadores, enquanto dos 40
por cento dos que não conseguiram passar só 30 por cento foram avaliados como
bons trabalhadores. Qual a probabilidade de que um empregado escolhido ao
acaso seja um bom trabalhador? Use aqui a técnica da árvore. Resp.: 0,60.
6 - Suponhamos que seja p a probabilidade de que o tempo (com sol ou nublado)
seja o mesmo do dia anterior. Se hoje for dia de sol, qual a probabilidade de que
depois de amanhã tenhamos também um dia de sol? Resp.: 2p2 − 2p + 1
1.11. EXERCÍCIOS
27
Teorema de Bayes
7 - Um saco contém três moedas, uma das quais foi cunhada com duas caras, enquanto as outras duas são normais e não viciadas. Uma moeda é retirada ao
acaso e jogada. Dado que o resultado foi cara, qual a probabilidade de que essa
seja a moeda de duas caras? Resp.: 0,5.
8 - As probabilidades de que três homens atinjam um alvo são, respectivamente,
1 1
, e 13 . Cada um atira uma vez em direção ao alvo.
6 4
a) Determine a probabilidade p de que exatamente um deles atinja o alvo.
Resp.: 0,431.
b) Se apenas um atinge o alvo, qual a probabilidade de ele ser o primeiro
homem? Resp.: 0,194.
28
CAPÍTULO 1. PROBABILIDADE
Capítulo 2
Variáveis Aleatórias: Discretas e
Contínuas
2.1
Introdução
Ao descrever um espaço amostral S associado a um experimento E, podemos observar que os resultados possíveis não são, necessariamente, núméricos. Consideremos,
por exemplo, o seguinte experimento:
E1 : Lançar duas moedas e observar a face superior de cada uma.
Neste experimento, temos S = {CC, CK, KC, KK} e, na prática, o que realmente
podemos estar interessados em observar é, por exemplo, o número de vezes que ocorre
cara (K), ou seja, temos interesse num número real que está associado a cada resultado
do espaço amostral S.
Definição 2.1.1 (Variável Aleatória). Seja E um experimento aleatório e S um
espaço amostral associado ao experimento. Dizemos que a função X é uma variável
aleatória quando associa a cada elemento do espaço amostral, s ∈ S, um número real,
x = X(s).
Notação: X, Y , Z, etc.
Esquematicamente, temos:
(Esboçar a função (ou variável aleatória) que associa a cada elemento
do espaço amostral, s ∈ S, um número real, x = X(s) )
29
30
CAPÍTULO 2. VARIÁVEIS ALEATÓRIAS: DISCRETAS E CONTÍNUAS
Exemplo 2.1.1. Considere o experimento E1 : Lançar duas moedas e observar a
seqüência de caras (K) e coroas (C).
Se X é a variável aleatória que representa o número de vezes que ocorre cara (K):
a) Descreva o espaço amostral, S, e obtenha os possíveis valores que a variável
aleatória X pode assumir.
b) Represente através de um gráfico o espaço amostral e a função X = X(s), isto
é, a variável aleatória X.
Solução:
Através do Exemplo 2.1.1, podemos notar que, ao descrever um espaço amostral
S associado a um experimento E, não necessariamente, um resultado individual é um
número. Neste exemplo, vimos que S = {KK, CK, KC, CC} e, na prática, o que
realmente podemos estar interessados em observar é o número de vezes que ocorre cara
(K), ou seja, temos interesse num número real que está associado a cada resultado do
espaço amostral S.
Definição 2.1.2 (Eventos Equivalentes). Sejam um experimento E e seu espaço
amostral S. Seja X uma variável aleatória definida em S e seja RX seu contradomínio.
Seja B um evento definido em relação a RX , isto é, B ⊂ RX . Defina o evento A como
A = {s ∈ S; X(s) ∈ B}.
Neste caso dizemos que A e B são eventos equivalentes.
Definição 2.1.3 (Probabilidade de Eventos Equivalentes). Seja B um evento
no contradomínio RX . Nesse caso, definimos P (B) da seguinte maneira:
P (B) = P (A),
onde A = {s ∈ S; X(s) ∈ B}.
2.2. VARIÁVEIS ALEATÓRIAS DISCRETAS
31
Exemplo 2.1.2. A partir do exemplo anterior, temos RX = {0, 1, 2}, onde cada um
desses valores ocorre com as seguintes probabilidades:
2.2
Variáveis Aleatórias Discretas
Definição 2.2.1 (Variável Aleatória Discreta). Dizemos que uma variável aleatória é discreta se o número de valores possíveis é finito ou infinito enumerável
(contável), de maneira que podemos listar todos os resultados como x1 , x2 , x3 , ....
Definição 2.2.2 (Função de Probabilidade). É a função p = p(xi ) que associa
uma probabilidade a cada valor xi da variável aleatória X.
Notação:
X
x1
P (X = xi ) = p(xi ) p(x1 )
x2
x3
...
p(x2 ) p(x3 ) . . .
Definição 2.2.3 (Distribuição de Probabilidades). Ao conjunto de todos os pares
[xi , p(xi )], i = 1, 2, ..., n, ... damos o nome de Distribuição de Probabilidades da
variável aleatória X, desde que:
1. p(xi ) ≥ 0, ∀i;
2. Σ∞
i=1 p(xi ) = 1.
Exemplo 2.2.1. A partir do Exemplo 2.1.1, obtenha a distribuição de probabilidades
da variável aleatória X e represente-a através de um gráfico.
32
CAPÍTULO 2. VARIÁVEIS ALEATÓRIAS: DISCRETAS E CONTÍNUAS
Exemplo 2.2.2. Considerando a variável aleatória (v.a.) X cuja função de probabilidade é dada por:
1
P (X = x) = x , x = 1, 2, 3, ...
2
a ) Mostre que X tem realmente uma distribuição de probabilidades.
b ) Faça um gráfico representando o comportamento desta distribuição.
c ) Obtenha:
i . P (X ser par)
ii . P (X ≥ 3)
iii . P (X ser múltiplo de 3)
2.3
Variáveis Aleatórias Contínuas
Definição 2.3.1 (Variável Aleatória Contínua). A variável aleatória X é contínua
se existir uma função f , denominada função densidade de probabilidade (f.d.p.) de X
que satisfaça às seguintes condições:
a) f (x) ≥ 0 para todo x;
R +∞
b) −∞ f (x)dx = 1.
Observações: Se X é uma variável aleatória contínua, então:
(i) P (X = k) = 0, onde k é qualquer valor real.
(ii) Para quaisquer a, b, com −∞ < a < b < +∞, teremos
2.4. FUNÇÃO DE DISTRIBUIÇÃO ACUMULADA
33
P (a ≤ X ≤ b) = P (a < X ≤ b)
= P (a ≤ X < b)
= P (a < X < b)
Z b
f (x)dx.
=
a
Probabilidade essa, que pode ser representada pela área sob o gráfico da função f
no intervalo [a, b], tal como ilustrado abaixo:
(Esboçar o gráfico representando a área definida por P (a < X < b) =
Rb
a
f (x)dx)
Exemplos:
1 - Suponha que estamos atirando dardos em um alvo circular de raio de 10 cm, e
seja X a distância do ponto atingido pelo dardo ao centro do alvo. A f.d.p. de
X é
kx, 0 ≤ x ≤ 10
f (x) =
0, c.c
a) Qual a probabilidade de acertar a mosca, se ela é um círculo de raio 1 cm?
b) Mostre que a probabilidade de acertar qualquer círculo concêntrico é proporcional a sua área.
2 - Uma variável aleatória contínua X é dita ter distribuição uniforme se a sua f.d.p.
é da forma
k, se a < x < b
f (x) =
0, caso contrário
a) Encontre o valor de k para que a função f seja realmente uma f.d.p.
b) Esboce o gráfico da distribuição de X.
2.4
Função de Distribuição Acumulada
Definição 2.4.1 (Função de Distribuição Acumulada - f.d.a.). A função de
distribuição acumulada F , ou simplesmente função de distribuição (f.d.) de uma
variável aleatória X qualquer é definida como
F (x) = P (X ≤ x),
∀ x ∈ <.
34
CAPÍTULO 2. VARIÁVEIS ALEATÓRIAS: DISCRETAS E CONTÍNUAS
Observação:
a) Se a variável aleatória X for discreta, então a função de distribuição será dada
por
F (x) = P (X ≤ x) =
X
p(xi ),
i ; xi ≤x
b) Se a variável aleatória X for contínua, então a função de distribuição será dada
por
Z
x
F (x) = P (X ≤ x) =
f (t)dt.
−∞
Exemplos:
1 - Suponhamos que a variável aleatória X tome os três valores 0,1 e 2, com probabilidades 1/3, 1/6 e 1/2, respectivamente. Encontre a função de distribuição F e
represente-a graficamente.
2 - Encontre a função de distribuição de X cuja f.d.p. é dada por
f (x) =
2x, 0 < x < 1,
0, c.c.
Esboçe os gráficos da f.d.p., f (x), e da função de distribuição F .
3 - Se a variável aleatória X tem distribuição uniforme obtenha a função de distribuição de X e represente-a graficamente.
2.4. FUNÇÃO DE DISTRIBUIÇÃO ACUMULADA
2.4.1
35
Propriedades da Função de Distribuição
A seguir veremos algumas propriedades importantes da função de distribuição
acumulada F de uma variável aleatória X qualquer:
(i) A função F é não decrescente.
(ii) F é contínua à direita.
(iii)
F (−∞) ≡ lim F (x) = 0
x→−∞
e
F (+∞) ≡ lim F (x) = 1.
x→+∞
Alguns Teoremas importantes relacionados à função de distribuição acumulada,
também são apresentados a seguir:
Teorema 2.4.1. Seja X uma variável aleatória discreta, com valores possíveis x1 , x2 , ...,
e suponha-se que esses valores tenham sido indexados de modo que x1 < x2 < .... Seja
F a função de distribuição de X. Então,
p(xi ) = P (X = xi ) = F (xi ) − F (x−
i ),
onde F (x−
i ) ≡ limh→0− F (xi + h).
Teorema 2.4.2. Seja F a função de distribuição de uma variável aleatória contínua,
com f.d.p. f . Então,
dF (x)
,
f (x) =
dx
para todo x no qual F seja derivável.
Observações:
1) Se X for uma variável aleatória discreta, o gráfico da função de distribuição
será constituído por segmentos de reta horizontais. Além disso, a função F é contínua,
exceto nos valores possíveis de X: x1 , ..., xn , ...; pois, para cada valor xi o gráfico
apresenta um salto de magnitude p(xi ) = P (X = xi ).
2) Se X for uma variável aleatória contínua, então
(i) P (a < X < b) = F (b) − F (a).
(ii) P (X > a) = 1 − F (a).
36
2.5
CAPÍTULO 2. VARIÁVEIS ALEATÓRIAS: DISCRETAS E CONTÍNUAS
Exercícios
1 - Sabendo-se que a v.a. X assume os valores 1,2 e 3 e que sua função de distribuição
F (x) é tal que
F (1) − F (1− ) = 1/4,
F (2) − F (2− ) = 1/2,
F (3) − F (3− ) = 1/4.
Obter a distribuição de X, a função de distribuição acumulada e seu respectivo
gráfico.
2 - Dada a seguinte função de distribuição
0,
x < 0,
F (x) =
−x
1 − e , x > 0.
a ) Encontre a probabilidade da variável X assumir os seguintes valores:
i . P (X = 1);
ii . P (0.5 < X < 1);
iii . P (X > 1);
d ) Esboçe um gráfico ilustrando cada uma das situações descritas acima.
e ) Determine o valor de α tal que F (α) = 1/4.
f ) Encontre a f.d.p. da variável X.
7 - Suponhamos que uma válvula eletrônica seja posta em um soquete e ensaiada.
Admitamos que a probabilidade de que o teste seja positivo seja 34 ; daí, a probabilidade de que seja negativo é igual a 14 . Adimitamos também que estejamos
ensaiando uma partida grande dessas válvulas. Os ensaios continuam até que a
primeira válvula positiva apareça. Considere a variável aleatória X: no de testes
necessários para concluir o experimento. Assim
S=
P (X = n) =
8 - Seja X o tempo até a desintegração de alguma partícula radioativa e suponha
que a função de distribuição de X seja dada por
0,
x < 0,
F (x) =
1 − e−λx , x > 0.
Suponha que λ seja tal que P (X ≥ 0, 01) = 1/2. Obtenha um número t tal que
P (X ≥ t) = 0, 9.
Capítulo 3
Caracterização Adicional das Variáveis
Aleatórias
3.1
Introdução
De maneira análoga ao que acontece na estatística descritiva (resumo de dados),
no estudo de variáveis aleatórias precisamos de algumas características numéricas
que possam nos fornecer uma idéia sobre o comportamento da distribuição de probabilidade. A estas características denominamos de parâmetros da distribuição.
Dois dos principais parâmetros são: o valor esperado e a variância. O valor
esperado de uma distribuição de probabilidades nos dá uma idéia de um valor médio
ou central da distribuição. Por outro lado, a medida que nos dá o grau de dispersão (ou
de concentração) dos valores assumidos pela variável em torno da média é a variância.
3.2
O Valor Esperado ou Esperança de Uma Variável
Aleatória
Definição 3.2.1 (Valor Esperado de uma Variável Aleatória).
Caso 1: Variável Aleatória Discreta
Seja X uma variável aleatória discreta, com valores possíveis x1 , x2 , ..., xn , ... Seja
p(xi ) = P (X = xi ), i = 1, 2, ..., n, ... Então, o valor esperado de X (ou esperança
matemática de X), denotado por E(X) é definido como
E(X) = Σ∞
i=1 xi p(xi ),
se a série definida acima convergir absolutamente, isto é, se
Σ∞
i=1 |xi | p(xi ) < ∞.
Este número é também denominado o valor médio de X, ou expectância de X.
37
38CAPÍTULO 3. CARACTERIZAÇÃO ADICIONAL DAS VARIÁVEIS ALEATÓRIAS
Caso 2: Variável Aleatória Contínua
Seja X uma variável aleatória contínua com f.d.p. f . Então, o valor médio de X
ou o valor esperado de X é definido como
Z
+∞
xf (x)dx.
E(X) =
−∞
Pode acontecer que esta integral (imprópria) não convirja. Conseqüentemente,
diremos que E(X) existirá se, e somente se,
Z
+∞
|x| f (x)dx
−∞
for finita.
Exemplos:
1 - Um fabricante produz peças tais que 10% delas são defeituosas e 90% delas são
não-defeituosas. Se uma peça defeituosa for produzida, o fabricante perde R$ 1,
enquanto uma peça não-defeituosa lhe dá um lucro de R$ 5. Se X for o lucro
líquido por peça, qual o valor esperado de X?
2 - Uma variável aleatória contínua X definida num intervalo [a, b] é dita ter distribuição uniforme se possui a seguinte f.d.p.
f (x) =
1
,
b−a
0,
a ≤ x ≤ b,
c.c.
Encontre a esperança dessa variável aleatória.
3 - Seja a variável aleatória X definida como segue. Suponha que X seja o tempo
(em minutos) durante o qual um equipamento elétrico seja utilizado em carga
máxima, em um certo período de tempo especificado. Suponha ainda, que X
seja uma variável aleatória contínua com a seguinte f.d.p.:
f (x) =


x
,
15002
−(x−3000)
,
15002

0,
0 ≤ x ≤ 1500,
1500 < x ≤ 3000,
c.c.
Encontre o tempo médio (em minutos) que o equipamento elétrico é utilizado em
carga máxima.
3.3. ESPERANÇA DE UMA FUNÇÃO DE UMA VARIÁVEL ALEATÓRIA
3.3
39
Esperança de uma Função de uma Variável Aleatória
É intuitivamente evidente a idéia de que qualquer função de uma variável aleatória
X, Y = H(X), também é uma variável aleatória, pois qualquer resultado aleatório,
X = x, resultará num resultado também aleatório Y = h(x) = y. Desta forma, terá
sentido calcular E(Y ).
Para se obter o valor esperado de Y = H(X) existem duas maneiras que se mostram equivalentes. A primeira requer que se obtenha primeiramente a distribuição de
Y ; problema este que será abordado posteriormente. Uma segunda maneira requer,
simplesmente, o conhecimento da distribuição de probabilidade de X.
Definição 3.3.1 (Esperança de uma Função de uma de uma Variável Aleatória). Seja
X uma variável aleatória e seja Y = H(X). Então,
(a) Se Y for uma variável aleatória discreta com valores possíveis y1 , y2 , ... e se
q(yi ) = P (Y = yi ), o valor esperado de Y é definido por
E(Y ) = Σ∞
i=1 yi q(yi ).
(b) Se Y for uma variável aleatória contínua com f.d.p. g, o valor esperado de Y
é definido por
Z +∞
E(Y ) =
yg(y)dy.
−∞
Teorema 3.3.1. Seja X uma variável aleatória e seja Y = H(X). Então,
(a) Se X for uma variável aleatória discreta e p(xi ) = P (X = xi ), tem-se que o
valor esperado de Y será dado por
E(Y ) = E[H(X)] = Σ∞
j=1 H(xj )p(xj ).
(b) Se X for uma variável aleatória contínua com f.d.p. f , tem-se que o valor
esperado de Y será dado por
Z
+∞
E(Y ) = E[H(X)] =
H(x)f (x)dx.
−∞
40CAPÍTULO 3. CARACTERIZAÇÃO ADICIONAL DAS VARIÁVEIS ALEATÓRIAS
3.4
Propriedades do valor esperado
Se X é uma v.a. e k é um valor qualquer, constante, então:
1. E[k] = k.
2. E[X + k] = E(X) + k.
3. E[kX] = kE(X).
4. E[X − µ] = 0, onde µ = E(X).
Demonstrações:
Exemplos:
1 - Um fabricante produz peças tais que 10% delas são defeituosas e 90% delas são
não-defeituosas. Se uma peça defeituosa for produzida, o fabricante perde R$
1,0, enquanto uma peça não-defeituosa lhe dá um lucro de R$ 5,0. Se X for o
lucro líquido por peça, determine:
a) O valor esperado de X.
b) Se houver um aumento de 10% nos valores de X, qual será o lucro líquido
esperado?
c) E Se houver um acréscimo de R$ 0,10 nos valores de X, em média, quanto
será o lucro líquido?
2 - Suponhamos que X seja uma variável aleatória com a seguinte f.d.p.
ex
, se x ≤ 0,
2
f (x) =
e−x
, se x > 0.
2
Se Y = |X|, qual será o valor de E(Y )?
3.5. A VARIÂNCIA DE UMA VARIÁVEL ALEATÓRIA
3.5
41
A Variância de uma Variável Aleatória
Definição 3.5.1 (Variância de uma Variável Aleatória).
Caso 1: Variável Aleatória Discreta
Dada a variável aleatória discreta X e a respectiva função de probabilidade p(x),
a variância de X é dada por
2
V ar(X) = E[(X − µ)2 ] = Σ∞
i=1 (xi − µ) p(xi ),
onde µ = E(X).
Caso 2: Variável Aleatória Contínua
Seja X uma variável aleatória contínua com f.d.p. f . Então, a variância de X é
dada por
R +∞
V ar(X) = E[(X − µ)2 ] = −∞ (x − µ)2 f (x)dx
A raiz quadrada da Variância de X é denominada Desvio Padrão de X, ou
seja,
DP (X) =
p
V ar(X).
Exercício:
1 - Mostre que
V ar(X) = E(X 2 ) − E 2 (X),
2
onde E(X 2 ) = Σ∞
i=1 xi p(xi ).
Exemplos:
1 - Um fabricante produz peças tais que 10% delas são defeituosas e 90% delas são
não-defeituosas. Se uma peça defeituosa for produzida, o fabricante perde R$
1,0, enquanto uma peça não-defeituosa lhe dá um lucro de R$ 5,0. Se X for o
lucro líquido por peça, determine o desvio padrão da v.a. X.
2 - Se X é uma variável aleatória uniforme num intervalo [a, b], ou seja, X ∼ U (a, b),
qual é o valor de V (X)?
3 - Seja V a velocidade do vento (em milhas por hora) e suponha-se que V seja
uniformemente distribuída sobre o intervalo [0, 10]. A pressão, digamos W (em
libras/pé quadrado), na superfície da asa de um avião é dada pela relação: W =
0, 003V 2 . Encontre o valor esperado de W .
42CAPÍTULO 3. CARACTERIZAÇÃO ADICIONAL DAS VARIÁVEIS ALEATÓRIAS
4 - Se X é uma variável aleatória contínua com f.d.p.
f (x) =
1 + x, −1 ≤ x ≤ 0,
1 − x. 0 ≤ x ≤ 1.
Obtenha a variância de X.
3.6
Propriedades da variância
Se X é uma v.a. e k é um valor qualquer, constante, então:
1. V ar(k) = 0.
2. V ar(X + k) = V ar(X).
3. V ar(kX) = k 2 V ar(X).
Demonstrações:
3.7. EXERCÍCIOS: VALOR ESPERADO E VARIÂNCIA
3.7
43
Exercícios: Valor Esperado e Variância
1 - Uma urna contém 4 bolas brancas e 6 pretas. 3 bolas são retiradas com reposição.
Seja X o número de bolas brancas. Calcular E(X) e D.P.(X). Resp.: E(X) =
1, 2.
2 - A função de probabilidade da variável aleatória X é: P (X = x) = 15 , para
X = 1, 2, 3, 4, 5. Calcular E(X) e E(X 2 ), e usando esses resultados calcular:
a) E(X + 3)2 ;
b) V ar(3X − 2).
Resp.: E(X) = 3, V ar(X) = 2, a) 38 b) 18.
3 - Um investidor julga que tem 0, 40 de probabilidade de ganhar R$25.000,00 e 0, 60
de probabilidade de perder R$15.000,00 num investimento.
a) Qual é o ganho esperado deste investidor?
b) Se G é o ganho líquido do investidor, qual será o ganho esperado de Y =
10G − 1000?
4 - Uma seguradora paga R$30.000,00 em caso de acidente de carro e cobra uma
taxa de R$1.000,00. Sabe-se que a probabilidade de que um carro sofra acidente
é de 3%. Quanto espera a seguradora ganhar por carro segurado? Resp.: E(L) =
100, 00
5 - Num jogo de dados, o jogador J1 paga R$ 20,00 ao jogador J2 e lança 3 dados.
E a seguinte regra é adotada:
(A) Se sair face 1 em um dos dados apenas, J1 ganha R$ 20,00
(B) Se sair face 1 em dois dados apenas, J1 ganha R$ 50,00
(C) Se sair 1 nos três dados, J1 ganha R$ 80,00
(A) Se nenhuma face 1 sair, J1 não recebe valor algum.
Nestas condições, qual o lucro líquido esperado pelo jogador J1 em uma jogada?
Você considera este jogo honesto? Por que? Resp.: R$ − 9, 21
44CAPÍTULO 3. CARACTERIZAÇÃO ADICIONAL DAS VARIÁVEIS ALEATÓRIAS
6 - Um banco pretende aumentar a eficiência de seus caixas. Para isto, o banco
está oferecendo um prêmio de R$ 150,00 para cada cliente atendido, além de 42
clientes por dia. O banco tem um ganho operacional de R$ 100,00 para cada
cliente atendido além de 41. As probabilidades de atendimento são:
no de clientes
Probabilidade
Até 41 42
0,88
0,06
43
0,04
44
0,01
45
0,006
46
0,004
Qual o ganho esperado do banco, se este novo sistema for implantado? O sistema
é vantajoso para o banco? Resp.: E(X) = 7, 30.
7 - Suponhamos que dez cartas estejam numeradas de 1 até 10. Das dez cartas,
retira-se uma de cada vez, ao acaso e sem reposição, até retirar-se o primeiro
número par. Se X é uma variável aleatória que expressa o número de retiradas
necessárias.
a) Qual é a função de probabilidade de X?
b) Em quantas retiradas espera-se obter o primeiro número par?
8 - Um vendedor de equipamentos pesado pode visitar, num dia, um ou dois clientes, com probabilidade de 1/3 ou 2/3, respectivamente. De cada contato, pode
resultar a venda de um equipamento por R$ 50.000,00(com probalidade 1/10)
ou nenhuma venda (com probabilidade 9/10). Indicando por Y o valor total de
vendas diárias desse vendedor:
a) Escreva a função de probabilidade de Y ;
b) Qual é o valor total esperado de vendas diárias?
Resp.: a) Y = {0, 50.000, 100.000} com probabilidades 126/150, 23/150, 1/150.
b) E(Y ) = 8.333, 33
9 - Calcule a variância do problema anterior.
10 - O tempo T , em minutos, necessário para um operário processar certa peça é uma
v.a. com a seguinte distribuição de probabilidade.
T =t
P (T = t)
2
0,1
3
0,1
4
0,3
5
0,2
6
0,2
7
0,1
a) Calcule o tempo médio de processamento.
Para cada peça processada, o operário ganha um fixo de R$ 2,00, mas, se ele
processa a peça em menos de seis minutos, ganha R$ 0,50 em cada minuto
poupado. Por exemplo, se ele processa a peça em quatro minutos, recebe a
quantia adicional de R$ 1,00.
b) Encontre a distribuição, a média e a variância da v.a. G: quantia ganha por
peça.
3.7. EXERCÍCIOS: VALOR ESPERADO E VARIÂNCIA
45
Resp.: a) E(T ) = 4, 6 b) E(G) = 2, 75 e V ar(G) = 0, 4125
11 - O serviço de meteorologia classifica o tipo de céu que é visível, em termos de
“graus de nebulosidade”. Uma escala de 11 categorias é empregada: 0,1,2,...,10,
onde 0 representa um céu perfeitamente claro, 10 representa um céu completamente encoberto, enquanto os outros valores representam as diferentes condições
intermediárias. Suponha-se que tal classificação seja feita em uma determinada
estação meteorológica, em um determinado dia e hora. Seja X a variável aleatória que pode tomar um dos 11 valores acima. Admita que a distribuição de
probabilidade de X seja
X=x
P (X = x)
0
1
2
3
4
5
6
7
8
9
10
0,05 0,15 0,15 0,06 0,06 0,06 0,06 0,06 0,15 0,15 0,05
Encontre E(X), E(X 2 ) e V ar(X).
12 - A percentagem de álcool (100X) em certo composto pode ser considerada uma
variável aleatória, onde X, tem a seguinte função densidade:
f (x) = 2x3 (1 − x), 0 < x < 1.
a) Obtenha a função de distribuição acumulada de X.
b) Calcule P (X ≤ 2/3)
c) Suponha que o preço de venda desse composto dependa do conteúdo de
álcool. Especificadamente, se 1/3 < X < 2/3, o composto é vendido por C1
u.m/galão; caso contrário, é vendido por C2 u.m/galão, determine o lucro
líquido médio por galão.
46CAPÍTULO 3. CARACTERIZAÇÃO ADICIONAL DAS VARIÁVEIS ALEATÓRIAS
Respostas
1)
2 ) E(X) = 1, 2 e V ar(X) =
3)
a) 38 ou 36?
b) 18.
4 ) E(X) = 7, 30
5)
6)
a) Y = {0, 50.000, 100.000} com probabilidades 126/150, 23/150, 1/150.
b) E(Y ) = 8.333.33
7)
8)
a) E(T ) = 4, 6
b) E(G) = 2, 75 e V ar(G) = 0, 4125
9)
Capítulo 4
Relação de Exercícios
Livro: "Estatística Básica". Wilton O. Bussab e Pedro A. Morettin. 5a. Edicão.
Capítulo 5 (Probabilidades):
Problema
1e2
5e6
8 e 12
15, 16, 18, 19 e 21
25
26, 27, 28 e 30
34 e 36
40 e 41
Página
105
106
110
115
121
122
123
124
Capítulo 6 (Variáveis Aleatórias Discretas):
Problema Página
1, 2 e 3
135
13 e 14
139
19
140
29 e 30
157
Capítulo 7 (Variáveis Aleatórias Contínuas):
Problema Página
2
166
5
171
10
172
28
194
47
48
CAPÍTULO 4. RELAÇÃO DE EXERCÍCIOS
Capítulo 5
Modelos Probabilísticos para Variáveis
Aleatórias Discretas
5.1
Introdução
Em muitas situações, alguns experimentos aleatórios apresentam características bastante peculiares. Este fato possibilita que, uma vez identificadas estas características,
um particular modelo probabilístico seja proposto para modelar o fenômeno em estudo.
É neste contexto, que passaremos ao estudo de alguns dos principais modelos
probabilísticos.
5.2
Distribuição de Bernoulli
Em muitos experimentos os resultados são tais que ocorre ou não ocorre determinada característica. Por exemplo:
1. Ao lançar uma moeda: o resultado ou é cara, ou não (ocorrendo, então, coroa);
2. Ao lançar um dado: ocorre número par ou não (ocorrendo número ímpar);
3. Uma pessoa é escolhida ao acaso dentre 1000: ou ela é do sexo masculino ou não
(é do sexo feminino);
4. Uma pessoa é escolhida ao acaso dentre 1000: ou ela é favorável a um determinado
projeto governamental ou não.
Em todas estes casos, estamos interessados na ocorrência (sucesso) ou não (fracasso) de determinada característica. Então, para cada experimento acima podemos
definir uma v.a. X, que assume valores: 1, se ocorrer sucesso, e 0, se ocorrer fracasso. E, indicaremos por p a probabilidade de sucesso, isto é, P (sucesso) = P (S) = p,
0 < p < 1.
49
50CAPÍTULO 5. MODELOS PROBABILÍSTICOS PARA VARIÁVEIS ALEATÓRIAS DISCRETAS
Definição 5.2.1 (Distribuição de Bernoulli). Uma variável aleatória X, que assume
apenas os valores 0 e 1; é dita ter distribuição de Bernoulli com parâmetro p, 0 < p < 1,
se sua função de probabilidade é dada por
p,
se x = 1
P (X = x) =
1 − p, se x = 0
Notação: X ∼ Ber(p).
Observação: Experimentos que resultam numa v.a. de Bernoulli são chamados
ensaios de Bernoulli.
Propriedades:
E(X) = p
V ar(X) = p(1 − p)
Exemplo 5.2.1.
1 - Ao lançar um dado perfeito, considere a variável X: ocorre
número menor que 3. Qual a distribuição de X. Obtenha os valores de E(X) e
V ar(X).
5.3
Distribuição Binomial
Definição 5.3.1 (Experimento Binomial). Um experimento binomial consiste de n
tentativas independentes de um mesmo experimento aleatório, onde cada tentativa adimite apenas dois resultados: sucesso com probabilidade p e fracasso com probabilidade
1 − p. Pode-se dizer ainda, que um experimento binomial consiste de n ensaios independentes de Bernoulli, cuja probabilidade de sucesso em cada ensaio é constante e
igual a p, 0 < p < 1.
Definição 5.3.2 (Variável Aleatória Binomial). Uma variável aleatória definida como
X: número de sucessos num experimento binomial é dita ser uma Variável aleatória
Binomial com parâmetros n e p.
Teorema 5.3.1. Se X é uma variável aleatória binomial com parâmetros n e p. Então
n
P (X = k) =
pk (1 − p)n−k , k = 0, 1, ..., n.
k
Notação: X ∼ B(n, p).
Propriedades:
E(X) = np
V ar(X) = np(1 − p)
5.4. DISTRIBUIÇÃO HIPERGEOMÉTRICA
51
Exemplo 5.3.1.
1 - Dos estudantes de um certo colégio, 41% fumam cigarro.
Numa pesquisa, pretende-se escolher seis estudantes ao acaso para darem sua
opinião sobre o fumo. Nesta pesquisa, qual é a probabilidade de
a) nenhum dos seis ser fumante?
b) todos serem fumantes?
c) pelo menos um fumar?
d) Quantos fumantes são esperados nesta pesquisa?
5.4
Distribuição Hipergeométrica
Considere uma população (conjunto) composta de N objetos, r dos quais têm
uma certa característica A, logo, N − r não têm a característica A (A). Suponha que
n desses objetos são escolhidos ao acaso sem reposição e que estamos interessados na
variável
X : número de elementos que possuem a característica A dentre os n.
Então, a variável definida desta forma é dita ter distribuição hipergeométrica com
parâmetros N , r e n e função de probabilidade dada por
r N −r x
n−x
P (X = x) =
, x = 0, 1, 2, ..., min(r, n).
N n
Notação: X ∼ hip(N, r, n).
Propriedades:
E(X) = np
−n
V ar(X) = np(1 − p) N
,
N −1
onde p = Nr é a probabilidade de se obter um objeto com a característica A numa
única extração.
Observação: Quando a população é muito grande, ou seja, N → ∞, quando
comparado com n, a retirada ao acaso, com ou sem reposição, serão praticamente
equivalentes, de modo que a distribuição hipergeométrica se aproxima da distribuição binomial.
52CAPÍTULO 5. MODELOS PROBABILÍSTICOS PARA VARIÁVEIS ALEATÓRIAS DISCRETAS
Exemplo 5.4.1.
1 - Em problemas de controle de qualidade, lotes com N itens
são examinados. O número de itens com defeito (atributo A), r, é desconhecido,
mas, digamos que, por experiências passadas, você sabe que em lotes de N = 100
peças, 10% são defeituosas. Se num certo lote de 100 peças você escolhe ao acaso
5 itens, sem reposição, qual é a probabilidade de:
a) nenhum item ser defeituoso?
b) não mais do que um item ser defeituoso?
c) Qual é o número esperado de itens defeituosos?
5.5
Distribuição de Poisson
Suponha, agora, que o interessse num certo experimento seja contar o número de
ocorrência de um certo evento, o qual pode ocorrer durante um intervalo de tempo, ao
longo de uma superfície ou volume. Por exemplo:
1. Durante o intervalo de uma hora, observar o número de carros que passam numa
rodovia;
2. Ao inspecionar a pintura de um carro, deseja-se observar o número de falhas;
3. Ao realizar o controle de qualidade de um produto alimentício, deseja-se conhecer
o número de bactérias.
Em todas estas condições poderemos trabalhar com a seguinte distribuição de
probabilidade.
Definição 5.5.1 (Distribuição de Poisson). Dizemos que a variável aleatória X :
número de ocorrência de um certo evento num determinado intervalo de tempo, superfície ou volume, tem distribuição de Poisson com parâmetro λ (λ > 0) se sua função
de probabilidade é dada por
P (X = x) =
e−λ λx
, x = 0, 1, 2, ...
x!
Notação: X ∼ P oisson(λ).
Propriedades:
E(X) = λ
V ar(X) = λ
Observação: Se X tem distribuição Binomial, ou seja, X ∼ B(n, p), em que n é
bastante grande com p pequeno, de sorte que np ≤ 7, então a distribuição de X se
aproxima da distribuição de Poisson com parâmetro λ = np, isto é, X ∼ P oisson(np).
Exemplos:
5.5. DISTRIBUIÇÃO DE POISSON
53
1 - Num livro de 800 páginas há 800 erros de impressão. Qual a probabilidade de
que uma página contenha pelo menos 3 erros?
2 - Seja X ∼ B(200, 0, 01). Calcular P (X = 10) usando a distribuição binomial e
compare com o valor aproximado pela Poisson.
54CAPÍTULO 5. MODELOS PROBABILÍSTICOS PARA VARIÁVEIS ALEATÓRIAS DISCRETAS
5.6
Exercícios: Modelos Probabilísticos Discretos
1 - Se X tem distribuição binomial com parâmetros n e p, utilize o fato de X ser a
soma de n ensaios de Bernoulli para calcular a média e a variância de X.
2 - Para os exercícios (a) a (e) abaixo, considere o enunciado:
Das variáveis abaixo descritas, assinale quais são binomiais, e para essas dê os
respectivos campos de definição e função de probabilidade. Quando julgar que a
variável não é binomial, aponte as razões de sua conclusão.
a) De uma urna com dez bolas brancas e 20 pretas, vamos extrair, com reposição, cinco bolas. X é o número de bolas brancas nas cinco extrações.
b) Refaça o problema anterior, mas dessa vez as n extrações são sem reposição.
c) Temos cinco urnas com bolas pretas e brancas e vamos extrair uma bola de
cada urna. Suponha que X seja o número de bolas brancas obtidas no final.
d) Vamos realizar uma pesquisa em dez cidades brasileiras, escolhendo ao acaso
um habitante de cada uma delas e classificando-o em pró ou contra um certo
projeto federal. Suponha que X seja o número de indivíduos contra o projeto
no final da pesquisa.
e) Em uma indústria existem 100 máquinas que fabricam determinada peça.
Cada peça é classificada como boa ou defeituosa. escolhemos ao acaso um
instatnte de tempo e verificamos uma peça de cada uma das máquinas.
Suponha que X seja o número de peças defeituosas.
3 - Sabendo-se que doze por cento dos que reservam lugar num vôo sistematicamente
faltam ao embarque e que o avião comporta 15 passageiros:
a) Determine a probabilidade de que todos os 15 que reservaram lugar compareçam ao embarque.
b) Se houve 16 pedidos de reserva, determine a probabilidade:
i) de uma pessoa ficar de fora;
ii) de nenhuma ficar de fora;
iii) de mais de uma ficar de fora.
4 - Se 3% dos habitantes de uma grande cidade são empregados do Governo, determine a probabilidade de:
a) Nenhum ser empregado do Governo numa amostra aleatória de 50 habitantes?
b) Encontrar no máximo 3 empregados do governo na amostra do item anterior?
5 - Um fabricante de peças de automóvel garante que uma caixa de suas peças conterá, no máximo, duas defeituosas. Se a caixa contém 20 peças, e a experiência
tem demonstrado que, em seu processo de fabricação, 6% das peças são defeituosas, qual é a probabilidade de que uma caixa satisfaça a garantia?
5.6. EXERCÍCIOS: MODELOS PROBABILÍSTICOS DISCRETOS
55
6 - Numa certa cidade, nascem por ano 40% de crianças do sexo masculino. Nas
famílias com 4 crianças, qual a probabilidade de:
a) todas serem homens;
b) todas serem mulheres;
c) todas serem do mesmo sexo;
d) haver a mesma quantidade de homens e mulheres.
7 - De acordo com as estimativas de uma companhia de seguros, a probabilidade de
incêndio numa casa é de 1% ao ano. A firma segura 400 casas.
a) Se muitos dos segurados vivem em casas adjacentes, por que tal circunstância pode invalidar o uso da distribuição binomial?
b) Suponha que os segurados morem em casas distantes umas das outras. Qual
a probabilidade de:
i) 0 incêndio?
ii) 1 incêndio?
8 - A probabilidade de um atirador acertar o alvo é 1/3. Se ele atirar 6 vezes, qual
a probabilidade de:
a) acertar exatamente 2 tiros;
b) não acertar tiro algum.
Resp.: a) 80/243 b) 64/729.
9 - Em seis lançamentos de um dado equilibrado, qual a probabilidade de ocorrer:
a) nenhuma vez a face 6;
b) 6 vezes a face 2;
c) pelo menos uma vez a face 4.
Resp.: a) 33.49% b) 0.0021% c) 66.51%
10 - Em Campina Grande, nascem por ano 52% de crianças do sexo masculino. Nas
famílias com 4 crianças, qual a probabilidade de:
a) todas serem homens;
b) todas serem mulheres;
c) todas serem do mesmo sexo;
d) haver a mesma quantidade de homens e mulheres.
Resp.: a) 7.31% b) 5.31% c) 12.62% d) 37.38%
11 - Uma prova é composta de 10 questões objetivas, onde cada questão possui 5
alternativas com apenas uma correta. Sabendo-se que um estudante não sabe
respondê-las e irá apelar inteiramente pela sorte. Qual a probabilidadede que:
56CAPÍTULO 5. MODELOS PROBABILÍSTICOS PARA VARIÁVEIS ALEATÓRIAS DISCRETAS
a) acerte 5 questões;
b) erre todas as questões;
c) acerte no mínimo 3 e, no máximo 5 questões;
d) qual o número esprerado de questões corretas?
Resp.: a) 2.64% b) 10.74% c) 31.58% d) 2
12 - Suponha que, em um determinado vôo, motores de avião falhem comprobabilidade igual a 0.4, e independente. Suponha ainda que um avião voa com segurança
se, pelo menos, metade dos seus motores não falha. Nestas condições, um avião
quadrimotor deverá ser preferido a um bimotor? Justifique sua resposta!
Resp.: Não! O vôo com segurança do bimotor é de 84%, contra 82.02% do
quadrimotor.
13 - Num determinado processo de fabricação 10% das peças são consideradas defeituosas. As peças são armazenadas em caixas com 5 unidades cada uma.
a) qual a probabilidade de haver, pelo menos 1, defeituosa numa caixa?
b) Se a empresa paga uma multa de R$ 10,00 por cada caixa em que houver,
pelo menos, uma peça defeituosa, qual o valor esperado da multa num total
de 1000 caixas?
Resp.: a) 40.95% b) R$4.095, 10
14 - Um produtor de sementes vende pacotes com 10 sementes cada. Os pacotes que
apresentarem mais de uma semente sem germinar serão indenizados. A probabilidade de uma semente germinar é de 0.8.
a) Qual a probabilidade de um pacote ser indenizado?
b) Se o produtor vender 1000 pacotes, qual o número esperado de pacotes indenizados?
c) Quando um pacote é indenizado, o produtor tem um prejuízo de R$ 1,20, e
se o pacote não for indenizado, tem um lucro de R$ de 2,50. Qual o lucro
líquido esperado por pacote?
Resp.: a) 62.42% b) 624 c) R$0, 19
Capítulo 6
Modelos Probabilísticos para Variáveis
Aleatórias Contínuas
6.1
Distribuição Uniforme
Definição 6.1.1 (Distribuição Uniforme). Uma variável aleatória contínua X é dita
ter distribuição uniforme se a sua f.d.p. é da forma
1
, se a < x < b
b−a
f (x) =
0, caso contrário
Notação: X ∼ U (a, b).
Propriedades:
E(X) =
a+b
2
e V ar(X) =
(b−a)2
12
(Construa um gráfico que ilustre a forma da f.d.p.
de uma uniforme qualquer)
Exemplo 6.1.1. Suponha que uma pane pode ocorrer em qualquer ponto de uma rede
elétrica de 10 Km. Obtenha a probabilidade de que uma pane ocorra em um ponto cuja
distância seja no máximo 1 Km das extremidades.
57
58CAPÍTULO 6. MODELOS PROBABILÍSTICOS PARA VARIÁVEIS ALEATÓRIAS CONTÍNUAS
6.2
Distribuição Exponencial
Definição 6.2.1 (Distribuição Exponencial). Uma variável aleatória contínua X,
assumindo todos os valores não negativos, terá distribuição exponencial com parâmetro
α > 0, se sua f.d.p. é dada por
f (x) =
αe−αx , x > 0
0, c.c.
Notação: X ∼ Exp(α).
Propriedades:
(i) E(X) =
1
α
e V ar(X) =
1
α2
(ii) A função de distribuição acumulada F de uma exponencial com parâmetro α é
dada por
F (x) = 1 − e−αx , x > 0.
(iii) (Falta de memória) Para todo s, t > 0, teremos
P (X > s + t | X > s) = P (X > t) .
(Construa um gráfico que ilustre a forma da f.d.p.
qualquer)
de uma exponencial
Exemplo: O tempo de vida (em horas) de um transistor pode ser considerado
uma variável aleatória com distribuição exponencial cuja média é igual a 500 horas.
De acordo com essas características, qual é a probabilidade de que um determinado
transistor dure mais do que a média?
6.3. DISTRIBUIÇÃO NORMAL (GAUSSIANA)
6.3
59
Distribuição Normal (Gaussiana)
A distribuição Normal é talvez a mais importante das distribuições de probabilidade, por razões que possivelmente ficarão claras ao longo deste curso. Erros de
mensuração de fenômenos físicos ou econômicos são freqüentemente modelados pela
distribuição Normal, mas esta não é a única aplicação desta densidade. Por exemplo,
a distribuição dos pesos, alturas e QI’s das pessoas numa população também já foram
modelados com sucesso por esta distribuição. A distribuição Normal tem a forma de
um sino, e possui dois parâmetros, µ e σ 2 .
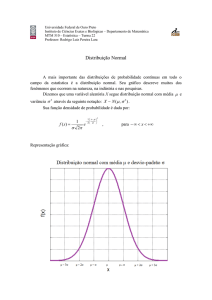
A distribuição Normal é também chamada de Gaussiana em homenagem ao matemático Carl Friederich Gauss (1777 - 1855), que a utilizou pela primeira vez na
modelagem de erros de medida. A distribuição Normal também funciona como uma
boa aproximação para outras densidades. Por exemplo, sob algumas condições pode-se
provar que a densidade Binomial pode ser aproximada pela Normal.
Definição 6.3.1 (Densidade Normal com média µ e variância σ 2 ). Seja X uma
variável aleatória contínua definida nos números reais. Dizemos que X tem densidade
Normal com média µ e variância σ 2 se a densidade de X é:
f (x) = √
1 x−µ 2
1
e− 2 ( σ ) .
2πσ
Notação: X ∼ N (µ, σ 2 )
Devemos dizer que o primeiro parâmetro, µ (lê-se: mi), é a média ou o valor
esperado de X, enquanto que o segundo parâmetro, σ 2 (lê-se: sigma dois), é a variância
de X. A seguir exibimos gráfico das distribuições Normais com média zero e variâncias
1, 2 e 4.
(Esboçar o gráfico de Distribuições Normais com média zero e variâncias
1, 2 e 4)
Note que o máximo das densidades é encontrado quando x = 0, isto é, quando x é
igual à média da distribuição. Isto vale para qualquer distribuição Normal: o máximo
de f (x) é obtido fazendo-se x = µ, onde µ é a média da Normal. Também, quanto
maior o valor da variância σ 2 , mais “espalhada” é a distribuição.
60CAPÍTULO 6. MODELOS PROBABILÍSTICOS PARA VARIÁVEIS ALEATÓRIAS CONTÍNUAS
6.3.1
Propriedades da Distribuição Normal
(1) f (x) dada pela expressão acima integra a 1, ou seja, a área sob a curva da normal
é igual a 1.
(2) f (x) ≥ 0, para qualquer valor real.
(3) Os limites de f (x) quando x tende a −∞ e +∞ são iguais a zero.
(4) A densidade N (µ, σ 2 ) é simétrica em torno de µ, ou seja: f (µ + x) = f (µ − x).
(5) O valor máximo de f (x) ocorre em x = µ.
(6) Os pontos de inflexão de f (x) são x = µ − σ e x = µ + σ.
Teorema 6.3.1. Se X ∼ N (µ, σ 2 ), então a variável aleatória definida por
Z=
X −µ
∼ N (0, 1),
σ
tem distribuição normal reduzida ou normal padrão.
Observações:
1) Se quisermos calcular a probabilidade de P (a < X < b), onde X ∼ N (µ, σ 2 ),
devemos resolver a seguinte integral:
Z b
1 x−µ 2
1
√
P (a < X < b) =
e− 2 ( σ ) dx,
2πσ
a
a qual não apresenta fácil solução. Por isso, a solução é reduzir (ou transformar) a
variável X para uma variável:
X −µ
,
Z=
σ
que tem distribuição normal padrão, e, assim obter a probabilidade de interesse na
Tabela da distribuição Normal Padrão.
2) Uma das Tabelas da distribuição Normal Padrão apresenta a seguinte probabilidade:
Z z
x2
1
√ e− 2 dx
P (0 < Z < z) =
2π
0
onde z é um valor real positivo.
A probabilidade dada por P (0 < Z < z) corresponde a seguinte área:
(Esboçar o gráfico representando a área referente a P (0 < Z < z))
6.3. DISTRIBUIÇÃO NORMAL (GAUSSIANA)
61
3) Uma outra Tabela da distribuição Normal Padrão apresenta a seguinte
probabilidade:
Z z
x2
1
√ e− 2 dx
P (−∞ < Z < z) =
2π
−∞
onde z é um valor real qualquer.
A probabilidade dada por P (−∞ < Z < z) corresponde a seguinte área:
(Esboçar o gráfico representando a área referente a P (−∞ < Z < z))
6.3.2
Exemplos do Uso da Tabela Normal Padrão
1. Considere X : N (100, 25), calcular:
a) P (100 ≤ X ≤ 106)
b) P (89 ≤ X ≤ 107)
c) P (112 ≤ X ≤ 116)
d) P (X ≥ 108)
2. Sendo X : N (50, 16), determinar xα , tal que:
a) P (X ≤ xα ) = 0, 05
b) P (X ≥ xα ) = 0, 99
6.3.3
Aproximação da Binomial pela Normal
Quando dispomos de uma amostra de tamanho n grande, e quando o produto da
proporção de sucesso na população (p) pelo tamanho da amostra resulta um valor
maior que cinco (np ≥ 5), o Teorema Central do Limite nos garante que a distribuição
normal constitui uma boa aproximação para a binomial, o que permite tratar uma
variável aleatória X ∼ Bin(n, p) como uma variável aleatória APROXIMADAMENTE
normal. Essa garantia facilita sobremaneira os cálculos de probabilidades, tendo em
62CAPÍTULO 6. MODELOS PROBABILÍSTICOS PARA VARIÁVEIS ALEATÓRIAS CONTÍNUAS
vista que podemos usar o fato de que, se X ∼ Bin(n, p), temos que E(X) = np e
V ar(X) = np(1 − p), e assim temos que
X − np
Z=p
≈ N (0, 1),
np(1 − p)
de onde temos que
P (a ≤ X ≤ b) ∼
=P
b − np
a − np
p
<Z< p
np(1 − p)
np(1 − p)
!
.
Do contrário, teríamos que encontrar tal probabilidade calculando
X n P (a ≤ X ≤ b) =
px (1 − p)n−x ,
x
o que, para n grande, se torna bastante inviável. No entanto, por aproximarmos
uma distribuição discreta por uma distribuição contínua, é necessário introduzir uma
correção, chamada de correção de continuidade. Esta correção consiste em subtrair 0,5
do valor inferior e somar 0,5 ao valor superior. Assim, temos:
!
a
−
0,
5
−
np
b
+
0,
5
−
np
P (a ≤ X ≤ b) ∼
<Z< p
.
=P p
np(1 − p)
np(1 − p)
Para justificar a correção de continuidade, basta atentar para a figura a seguir,
sem perda de generalidade, que representa uma variável aleatória X ∼ Bin(10, 1/2).
Neste caso, temos que E(X) = 10 ×
P (6 ≤ X ≤ 8) ∼
=
Observações importantes:
1
2
= 5 e, por exemplo:
6.3. DISTRIBUIÇÃO NORMAL (GAUSSIANA)
63
1) Note que P (5 < X ≤ 8) = P (6 ≤ X ≤ 8), pois a distribuição Binomial é discreta;
2) Para calcular a probabilidade P (X = a), criamos um intervalo artificial, pois
com variáveis contínuas essa probabilidade seria zero. Assim,
!
a
−
0,
5
−
np
a
+
0,
5
−
np
P (X = a) ∼
<Z< p
.
=P p
np(1 − p)
np(1 − p)
Aplicação:
O câncer uterino em cadelas pode ser curado através de procedimento cirúrgico
em 40% dos casos. Dentre as cadelas que têm essa doença, selecionamos 15, as quais
serão submetidas à cirurgia. Fazendo alguma suposição adicional que julgar necessária,
responda qual é a probabilidade de:
a) Todas serem curadas?
b) Pelo menos duas não serem curadas?
c) Ao menos 10 ficarem livres da doença?
64CAPÍTULO 6. MODELOS PROBABILÍSTICOS PARA VARIÁVEIS ALEATÓRIAS CONTÍNUAS
6.4
Exercícios: modelos de variáveis contínuas
1 ) Escolhe-se, aleatoriamente, um ponto no intervalo [0;10]. Qual a probabilidade
de que o ponto esteja entre 3/2 e 7/2? E entre 7/2 e 23/2? Resp.: 20% e 65%
2 ) Com o objetivo de verificar a resistência à pressão de água, os técnicos de qualidade de uma empresa inspecionam os tubos de PVC produzidos. Os tubos
produzidos têm 6 metros de comprimento e são submetidos a grandes pressões
até o aparecimento do primeiro vazamento, cuja distância a uma das extremidades (fixada a priori) é anotada para fins de análise posterior. Escolhe-se um tubo
ao acaso para ser inspecionado. Seja X a variável aleatória que indica a distância correspondente ao vazamento. Admita que a probabilidade de ocorrência de
vazamento em todos os pontos são iguais.
a) Calcule a probabilidade de que o vazamento esteja, no máximo, a 1 metro
da extremidade fixada;
b) Calcule a probabilidade de que o vazamento esteja a uma distância entre 3
metros e 4 metros da extremidade fixada;
c) Existe alguma coincidência entre os resultados obtidos em (a) e (b)? Justifique sua resposta.
Resp.: a) 16, 7% b) 16, 7%
3 ) Consideremos um relógio eletrônico, onde o ponteiro dos segundos tem um movimento contínuo. Definamos a variável aleatória X = ângulo formado pelo
ponteiro dos segundos e pelo eixo que passa pelo número 12 e vai até o centro.
a) Identifique o conjunto dos possíveis valores de X.
b) Calcule a probabilidade de que, olhando para este relógio em um momento
escolhido ao acaso, encontrar ângulo X entre 120 graus e 240 graus.
Resp.: a) RX = [0, 360◦ ) b) 33, 3%
4 ) O tempo necessário para um medicamento contra dor fazer efeito foi modelado
de acordo com a densidade Uniforme no intervalo de 5 a 15 minutos, tendo por
base experimentos conduzidos em animais. Um paciente, que esteja sofrendo dor,
recebe o remédio e, supondo válido o modelo mencionado acima, pergunta-se a
probabilidade da dor:
a) Cessar em até 10 minutos?
b) Demorar pelo menos 12 minutos?
c) Durar mais de 7 minutos, sabendo-se que durou menos de 10?
Resp.: a) 50% b) 30% c) 60%
5 ) Admite-se que uma pane pode ocorrer em qualquer ponto de uma rede elétrica
de 10 quilômetros.
6.4. EXERCÍCIOS: MODELOS DE VARIÁVEIS CONTÍNUAS
65
a) Qual é a probabilidade da pane ocorrer nos primeiros 500 metros? E de
ocorrer nos 3 quilômetros centrais da rede?
b) O custo de reparo da rede depende da distância do centro de serviço ao local
da pane. Considere que o centro de serviço está na origem da rede e que o
custo é de R$ 200 para distâncias até 3 quilômetros, de R$ 400 entre 3 e 8
quilômetros e de R$ 1.000 para distâncias acima de 8 quilômetros. Qual é
o custo médio do conserto?
Resp.: a) 5% e 30% b) R$460, 00
6 ) Suponha que o valor esperado de uma variável aleatória com distribuição Uniforme contínua é igual a 1 e a variância é 1/12. Encontre a probabilidade da
variável assumir valores menores que 3/4. Resp.: 25%
7 ) Seja V a velocidade do vento (em milhas por hora) e suponha-se que V seja
uniformemente distribuída sobre o intervalo [0, 10]. A pressão, digamos W (em
libras/pé quadrado), na superfície da asa de um avião é dada pela relação: W =
0, 003V 2 . Encontre o valor esperado de W . Resp.: 0, 1
8 ) O tempo de vida (em horas) de um transistor é uma variável aleatória T com
f.d.p.
1 − 1 t
e 500 , t > 0
500
f (t) =
0, c.c.
Encontre:
a) A vida média do transistor;
b) A probabilidade de que seu tempo de vida seja maior do que a média.
Resp.: a) 500 horas b) 36, 79%
9 ) Estima-se que o tempo de falha de um tubo de televisão seja distribuído exponencialmente, com uma média de três anos. Uma companhia oferece seguro para
esses tubos no primeiro ano de uso. Qual a porcentagem de apólices que terão
que pagar? Resp.: 28, 35%
10 ) Suponha que, em determinado período do dia, o tempo médio de atendimento em
um caixa de banco seja de 5 minutos. Admitindo que o tempo para atendimento
tenha distribuição exponencial, determinar a probabilidade de um cliente:
a) Esperar mais de 5 minutos para ser atendido;
b) Esperar até 5 minutos para ser atendido;
c) Esperar entre 3 e 8 minutos para ser atendido.
Resp.: a) 36, 79% b) 63, 21% c) 34, 69%
11 ) O tempo de atendimento em uma oficina é aproximadamente exponencial com
parâmetro α = 1/4. Qual a probabilidade de:
66CAPÍTULO 6. MODELOS PROBABILÍSTICOS PARA VARIÁVEIS ALEATÓRIAS CONTÍNUAS
a) Esperar no mínimo 4 minutos?
b) Espera inferior a 5 minutos?
c) Espera de exatamente 4 minutos?
Resp.: a) 36, 79% b) 71, 35% c) Zero
12 ) O tempo, em minutos, de utilização de um caixa eletrônico por clientes de um
certo banco, foi modelado por uma variável aleatória T com distribuição Exponencial cuja média é igual a 1/3. Determine:
a) P(T < 1).
b) P(T > 1 | T ≤ 2).
c) Um número a tal que P(T ≤ a) = 0,4.
Resp.: a) 95, 02% b) 4, 74% c) 0, 1703
13 ) Para uma variável aleatória com distribuição Exponencial de parâmetro igual a
1, determine a probabilidade de sorteamos um valor que se distancie no máximo
0,5 da média. Resp.: 38, 34%
14 ) Uma v.a X tem Distribuição Normal, com média 50 e desvio padrão 10, isto é,
X ∼ N (50; 102 ), determine o valor de A, B e C, nos seguintes casos:
a) P(X > A) = 0, 0228;
b) P(X < B) = 0, 0668;
c) P(|X − µ| < C) = 0, 6826;
Resp.: a) 70 b) 35 c) 10
15 ) Uma fábrica de carros sabe que a duração (X) dos motores de sua fabricação
tem distribuição aproximadamente normal, com média de 150.000 km e desvio
padrão de 5.000 km, ou seja, X ∼ N (150.000; 5.0002 ). Qual a probabilidade de
que um carro, escolhido ao acaso, dos fabricados por essa firma, tenha um motor
que dure:
a) menos de 170.000 km?
b) entre 140.000 km e 165.000 km?
c) se a fábrica substitui o motor que apresenta duração inferior à garantia (g),
qual deve ser esta garantia, para que a porcentagem de motores substituídos
seja aproximadamente igual a 0, 2%?
Resp.: a) 99, 997% b) 97, 59% c) g = 135600km
16 ) Foi feito um estudo sobre a altura (X) dos alunos de uma faculdade, observandose que ela se distribuia com média 160 cm e variância 64 cm2 . Determinar:
a) P (X ≤ 176) ;
6.4. EXERCÍCIOS: MODELOS DE VARIÁVEIS CONTÍNUAS
67
b) P(|X − 160| ≤ 8) ;
c) a porcentagem dos alunos com altura acima de 180 cm.
Resp.: a) 97, 725% b) 68, 268% c) 0, 621%
17 ) Um fabricante de máquinas de lavar sabe, por longa experiência, que a duração
de suas máquinas tem distribuição normal com média 1000 dias e desvio padrão
de 200 dias. Se este fabricante oferece uma garantia de 1 ano (365 dias) e produz
mensalmente 2000 máquinas, quantas máquinas ele espera trocar pelo uso da
garantia dada, mensalmente? Resp.: Aproximadamente uma.
18 ) Avaliou-se que o tempo médio desperdiçado em cirurgias de longa duração (mais
de 4 horas) é uma variável aleatória Normal com média de 90 min. e desvio
padrão de 50 min.
a) Qual é a probabilidade de uma determinada cirurgia ter um desperdício de
tempo de pelo menos 60 min. ?
b) Qual é a probabilidade de haver um desperdício de tempo de até 50 min.?
c) 15% das cirurgias tem um tempo de desperdício muito alto. Acima de que
valor esse tempo é considerado muito alto?
d) Em 100 cirurgias de longa duração realizadas em um certo mês, quantas
esperamos encontrar com um desperdício superior a 2 horas?
e) Em um determinado dia, foram realizadas 4 cirurgias de longa duração.
Qual é a probabilidade de nenhuma ter tido um desperdício superior a 50
min.?
Resp.: a) 72, 575% b) 21, 186% c) 142 minutos d) Aproximadamente 27 e) 0, 201%
19 ) Numa fábrica foram instaladas 1.000 lâmpadas novas. Sabe-se que a duração
média das lâmpadas é de 800 horas e desvio padrão de 100 horas, com distribuição
normal. Qual o número esperado de lâmpadas que durarão:
a) menos de 500 horas;
b) mais de 700 horas;
c) entre 516 e 814.
Resp.: a) Aproximadamente 1 b) Aproximadamente 841 c) Aproximadamente
553
20 ) O preço de um produto se distribui normalmente com preço médio µ e desvio
padrão σ. Sabe-se que 81,98% dos preços estão situados entre (µ − 10) e (µ +
10), sendo que, 42,07% dos preços são superiores a 600 reais. Baseado nessas
informações, determine µ e σ. Resp.: µ ∼
= 599, 41 e σ ∼
= 7, 463
21 ) A vida útil (em anos) de um computador pessoal tem distribuição aproximadamente normal com média de 3,9 anos e desvio padrão de 1,96 anos.
68CAPÍTULO 6. MODELOS PROBABILÍSTICOS PARA VARIÁVEIS ALEATÓRIAS CONTÍNUAS
a) Que proporção dos computadores falhará no primeiro ano?
b) Que proporção dos computadores durará quatro anos ou mais?
c) Que proporção dos computadores durará no mínimo dois anos?
d) Que proporção dos computadores durará mais de 2,5 anos, porém menos de
quatro anos?
e) Se o fabricante adota uma política de garantia segundo a qual apenas 5%
dos computadores têm de ser substituídos, qual é o período dessa garantia?
Resp.: a) 6, 944% b) 48, 006% c) 83, 398% d) 28, 109% e) g = 0, 6856 ano
6.5. EXERCÍCIOS: DISTRIBUIÇÃO NORMAL
6.5
69
Exercícios: Distribuição Normal
1 ) Se a variável Z tem distribuição normal padrão, isto é, Z ∼ N (0; 1), obtenha:
a) P (0 ≤ Z ≤ 1, 96);
b) P (Z < 1, 64);
c) P (Z < −2, 57);
d) o valor z, na tabela da normal padrão, tal que, P (Z < z) = 0, 025.
Resp.: a)
2 ) Seja X uma v.a, tal que, X ∼ N (100; 25), determinar:
a) P (X ≥ 108);
b) P (X = 100);
c) P (89 ≤ X ≤ 107);
d) P (12 < X − µ < 16);
e) P (112 < X < 116);
f) P (X < 100 ou X > 106);
Resp.: a)
3 ) Uma v.a X tem Distribuição Normal, com média 50 e desvio padrão 10, i.é,
X ∼ N (50; 102 ), determine o valor de A, B e C, nos seguintes casos:
a) P(X > A) = 0, 0228;
b) P(X < B) = 0, 0668;
c) P(|X − µ| < C) = 0, 6826;
Resp.: a)
70CAPÍTULO 6. MODELOS PROBABILÍSTICOS PARA VARIÁVEIS ALEATÓRIAS CONTÍNUAS
4 ) Uma fábrica de carros sabe que a duração (X) dos motores de sua fabricação
tem distribuição aproximadamente normal, com média de 150.000 km e desvio
padrão de 5.000 km, ou seja, X ∼ N (150.000; 5.0002 ). Qual a probabilidade de
que um carro, escolhido ao acaso, dos fabricados por essa firma, tenha um motor
que dure:
a) menos de 170.000 km?
b) entre 140.000 km e 165.000 km?
c) se a fábrica substitui o motor que apresenta duração inferior à garantia (g),
qual deve ser esta garantia, para que a porcentagem de motores substituídos
seja inferior a 0, 2%?
Resp.: a)
5 ) Foi feito um estudo sobre a altura (X) dos alunos de uma faculdade, observandose que ela se distribuia com média 160 cm e variância 64 cm2 . Determinar:
a) P (X ≤ 176) ;
b) P(|X − 160| ≤ 8) ;
c) a porcentagem dos alunos com altura acima de 180 cm.
Resp.: a)
6 ) Um fabricante de máquinas de lavar sabe, por longa experiência, que a duração
de suas máquinas tem distribuição normal com média 1000 dias e desvio padrão
de 200 dias. Se este fabricante oferece uma garantia de 1 ano (365 dias) e produz
mensalmente 2000 máquinas, quantas máquinas ele espera trocar pelo uso da
garantia dada, mensalmente?
7 ) Avaliou-se que o tempo médio desperdiçado em cirurgias de longa duração (mais
de 4 horas) é uma variável aleatória Normal com média de 90 min. e desvio
padrão de 50 min.
a) Qual é a probabilidade de uma determinada cirurgia ter um desperdício de
tempo de mais de 60 min. ?
b) Qual é a probabilidade de haver um desperdício de tempo de no máximo 50
min.?
c) 15% das cirurgias tem um tempo de desperdício muito alto. Acima de que
valor esse tempo é considerado muito alto?
d) Em 100 cirurgias de longa duração realizadas em um certo mês, quantas
esperamos encontrar com um desperdício superior a 2 horas?
e) Em um determinado dia, foram realizadas 4 cirurgias de longa duração.
Qual é a probabilidade de nenhuma ter tido um desperdício superior a 50
min.?
6.5. EXERCÍCIOS: DISTRIBUIÇÃO NORMAL
71
f) Cada hora ou fração da hora desperdiçada em uma cirurgia custa ao hospital
R$ 56,00. Sabendo que acima de 2 horas de desperdício o prejuízo é fixo no
valor de R$ 200,00, obtenha o prejuízo esperado.
8 ) Numa fábrica foram instaladas 1.000 lâmpadas novas. Sabe-se que a duração
média das lâmpadas é de 800 horas e desvio padrão de 100 horas, com distribuição
normal. Qual a quantidade de lâmpadas que durarão:
a) menos de 500 horas;
b) mais de 700 horas;
c) entre 516 e 814.
Resp.: a)
9 ) O preço de um produto se distribui normalmente com preço médio µ e desvio
padrão σ. Sabe-se que 81,98% dos preços estão situados entre (µ − 10) e (µ + 10),
sendo que, 42,07% dos preços são superiores a 600g. Baseado nessas informações,
determine µ e σ. Resp.: a)
10 ) A vida útil (em anos) de um computador pessoal tem distribuição aproximadamente normal com média de 2,9 anos e desvio padrão de 1,96 anos.
a) Que proporção dos computadores falhará no primeiro ano?
b) Que proporção dos computadores durará quatro anos ou mais?
c) Que proporção dos computadores durará no mínimo dois anos?
d) Que proporção dos computadores durará mais de 2,5 anos, porém menos de
quatro anos?
e) Se o fabricante adota uma política de garantia segundo a qual apenas 5%
dos computadores têm de ser substituídos, qual é o período dessa garantia?
Resp.: a)
11 ) Mostre que, em qualquer distribuição normal, a área sob a curva, determinada
pelos intervalos abaixo, é sempre a mesma e independe dos parâmetros da distribuição:
a) (µ − σ; µ + σ);
b) (µ − 2σ; µ + 2σ);
c) (µ − 3σ; µ + 3σ);
Esboce um gráfico para cada uma dessas situações.
Resp.: a)
72CAPÍTULO 6. MODELOS PROBABILÍSTICOS PARA VARIÁVEIS ALEATÓRIAS CONTÍNUAS
Respostas a serem confirmadas
1)
a) 0, 0547 = 5, 47%
b) 0%
c) 0, 9053 = 90, 53%
d) 0, 0075 = 0, 75%
e) 0, 6151 = 61, 51%
2)
a) A = 70;
b) B = 35;
c) C = 10.
3)
a) 0, 999968 = 99, 99% ∼
= 100%
b) 0, 976 = 97, 6%
c) g = 135.650 km
4)
a) 97, 72%
b) 68, 26%
c) 0, 62%
5)
a) 1, 4 ∼
=1
b) 841, 3 ∼
= 841
c) 553, 4 ∼
= 553
Capítulo 7
Variáveis Aleatórias Bidimensionais
7.1
Introdução
Na maioria das situações dificilmente trabalhamos com apenas uma variável aleatória.
É muito comum estarmos interessados no comportamento conjunto de várias variáveis
aleatórias. Trataremos aqui apenas de duas variáveis, porém, os conceitos estudados
aqui podem ser expandidos de maneira análoga para mais de duas variáveis.
7.2
Variáveis Aleatórias Discretas
Iniciaremos nosso estudo de variáveis aleatórias bidimensionais considerando o caso
discreto e através do seguinte exemplo:
Uma amostra de 20 alunos do primeiro ano de uma faculdade foi escolhida. Perguntouse aos alunos se trabalhavam, variável que foi representada por X, e o número de vestibulares prestados, variável representada por Y . Os dados obtidos estão na tabela
abaixo.
X
Y
não sim
1
1
X
Y
não
2
não não não
2
1
1
não sim
2
1
não sim
3
2
sim
2
sim
3
não sim
1
1
sim
1
não não
2
2
não sim
1
3
não
2
Podemos coletar as freqüências de ocorrência dos possíveis pares, construindo uma
tabela de freqüência conjunta de X e Y .
73
74
CAPÍTULO 7. VARIÁVEIS ALEATÓRIAS BIDIMENSIONAIS
(X, Y )
freqüência
Total
Esta mesma tabela pode ser apresentada de maneira mais conveniente através da
tabela de dupla entrada, da seguinte forma:
X|Y
Total
Total
Dessa forma, fica facilitada a tarefa de obter a tabela de freqüência individual
para cada variável que, pela posição em que seus valores aparecem na tabela de dupla
entrada, é chamada de tabela marginal de freqüência da variável X (ou Y ), ou simplesmente marginal de X (ou Y ). Temos então para as variáveis X e Y , do exemplo
anterior, as seguintes tabelas de freqüência:
X
Total
freqüência
Y
freqüência
Total
Observe que podemos construir as mesmas tabelas considerando as freqüências
relativas.
7.2.1
Função de Probabilidade Conjunta
Iremos considerar agora o caso de variáveis aleatórias discretas, definidas a partir das
suas funções de probabilidades. Iniciamos estendendo a definição de função de probabilidade para o caso de duas variáveis.
Definição 7.2.1 (Função de probabilidade conjunta(bidimensional)). Seja X
uma variável aleatória que assume os valores x1 , x2 , ..., xn e Y variável aleatória que
assume os valores y1 , y2 , ..., ym . A função de probabilidade conjunta é definida,
para todos os possíveis pares de valores (xi , yj ), i = 1, 2, ..., n e j = 1, 2, ..., m, da
seguinte forma:
p(xi , yj ) = P [(X = xi ) ∩ (Y = yj )] = P (X = xi , Y = yj ),
isto é, p(xi , yj ) representa a probabilidade de (X, Y ) ser igual a (xi , yj ).
7.2. VARIÁVEIS ALEATÓRIAS DISCRETAS
75
Definição 7.2.2 (Distribuição conjunta(bidimensional) de probabilidades).
Ao conjunto de pares
{(xi , yj ), p(xi , yj ), i = 1, 2, ..., n j = 1, 2, ..., m},
damos o nome de distribuição conjunta de probabilidades da variável aleatória bidimensional (X, Y ), onde:
n X
m
X
p(xi , yj ) = 1
i=1 j=1
A distribuição conjunta de probabilidades da variável (X, Y ) pode ser representada, também, através de uma tabela de dupla entrada.
Exemplo 7.2.1. Uma região foi subdividida em 10 sub-regiões. Em cada uma delas,
foram observadas duas variáveis: número de poços artesianos (X) e número de riachos
ou rios presentes na sub-região (Y ). Os resultados são apresentados na tabela a seguir:
Sub-região 1 2
X
0 0
Y
1 2
3 4 5 6
0 0 1 2
1 0 1 0
7 8 9
1 2 2
0 1 2
10
0
2
Considerando que escolhemos uma das sub-regiões ao acaso, isto é, cada sub-região
tem mesma probabilidade 1/10 de ser escolhida, podemos construir a distribuição de
probabilidades conjunta de (X, Y ), tal como:
(X, Y ) P (X, Y )
Total
Cuja tabela de dupla entrada é dada por:
X|Y
Total
Total
76
CAPÍTULO 7. VARIÁVEIS ALEATÓRIAS BIDIMENSIONAIS
7.2.2
Distribuições Marginais de Probabilidades
Quando trabalhamos com uma variável aleatória bidimensional podemos ter o interesse
em estudar o comportamento de uma única variável; ou seja; em conhecer a distribuição
de probabilidade de X ou de Y . Para isto precisamos considerar a distribuição de
probabilidades conjunta de (X, Y ) representada em uma tabela de dupla entrada, tal
como:
Tabela 1: tabela de dupla entrada para
(X,Y).
Y
y1
...
yn
X
x1
p(x1 , y1 ) ... p(x1 , yn )
p(x2 , y1 ) ... p(x2 , yn )
x2
...
...
...
...
...
...
...
...
xm
p(xm , y1 ) ... p(xm , yn )
Total
p(y1 )
...
p(yn )
apresentar a distribuição conjunta de
Total
p(x1 )
p(x2 )
...
...
p(xm )
1,0
Desta maneira, a distribuição de X ou comumente denominada de distribuição
marginal de X, pode ser obtida a partir de
p(xi ) = P [(X = xi , Y = y1 )ou(X = xi , Y = y2 )ou...ou(X = xi , Y = ym )] = Σm
j=1 p(xi , yj ).
De modo análogo, a distribuição marginal de Y é obtida a partir de
p(yj ) = P [(X = x1 , Y = yj )ou(X = x2 , Y = yj )ou...ou(X = xn , Y = yj )] = Σni=1 p(xi , yj ).
Exemplo 7.2.2. Considerando o exemplo das sub-regiões, podemos calcular, através
da distribuição conjunta, as seguintes distribuições marginais:
X = xi
0
P (X = xi )
7.2.3
1
Y = yj
P (Y = yj )
2
0
1
2
Distribuição Condicional
Definição 7.2.3 (Probabilidade condicional). Seja xi um valor de X, tal que
P (X = xi ) = p(xi ) > 0. A probabilidade
P (Y = yj |X = xi ) =
P (X = xi , Y = yj )
,
P (X = xi )
j = 1, . . . , m,
é denominada probabilidade condicional de Y = yj , dado que X = xi .
7.2. VARIÁVEIS ALEATÓRIAS DISCRETAS
77
Caso P (X = xi ) = 0, a probabilidade condicional pode ser definida arbitrariamente e adotaremos P (Y = yj | X = xi ) = P (Y = yj ).
Podemos observar que para xi fixado, os pares (yj , P (Y = yj |X = xi )), j =
1, . . . , m, definem a distribuição condicional de Y , dado que X = xi (Verifique que
além das probabilidades serem não-negativas a soma das probabilidades é igual a 1).
Definição 7.2.4 (Esperança condicional). A esperança condicional de X, dado
que Y = yj , é definida por
E(X|Y = yj ) =
n
X
xi P (X = xi |Y = yj )
i=1
De modo análogo define-se E(Y |X = xi )
7.2.4
Independência
Definição 7.2.5 (Variáveis aleatórias independentes). As variáveis aleatórias X
e Y , assumindo os valores x1 , x2 , . . . e y1 , y2 , . . ., respectivamente, são independentes
se a ocorrência de qualquer valor de uma delas não altera a chance de ocorrência de
valores da outra. Ou seja,
P (X = xi | Y = yj ) = P (X = xi ),
para todos os possíveis valores (xi , yj ) das variáveis (X, Y ). Como definição alternativa
podemos usar:
P (X = xi , Y = yj ) = P (X = xi )P (Y = yj ),
para quaisquer (xi , yj ).
Caso P (Y = yj ) = 0, a probabilidade condicional pode ser definida arbitrariamente
e adotaremos P (X = xi | Y = yj ) = P (X = xi ).
Observação: X e Y são independentes ⇐⇒ p(xi , yj ) = p(xi )p(yj ), ∀ (xi , yj ).
Se existe pelo menos um par (x0 , y0 ) tal que:
p(xo , y0 ) 6= p(x0 )p(y0 )
então, X e Y não são independentes.
Exemplo 7.2.3. Suponhamos que X e Y tenham distribuição conjunta dada pela seguinte tabela:
78
CAPÍTULO 7. VARIÁVEIS ALEATÓRIAS BIDIMENSIONAIS
X|Y
1
2
3
1
2
3
0 1/5 0
1/5 1/5 1/5
0 1/5 0
Determine as distribuições marginais de X e Y e verifique se estas variáveis são
independentes.
Exemplo 7.2.4. A partir do exemplo 7.2.1 verifique se as variáveis X e Y são independentes e caso não sejam, obtenha uma das distribuições condicionais.
7.2.5
Função de Variáveis Aleatórias Discretas
Em algumas situações poderá surgir o interesse em estudar o comportamento de uma
função das variáveis aleatórias, tal como: soma, produto ou alguma outra relação
entre elas. Para melhor compreender os procedimentos para se realizar tal estudo,
consideremos o seguinte exemplo:
Exemplo 7.2.5. Em uma cidade do Estado de São Paulo, admite-se que o número
de anos para completar o ensino fundamental (variável F ) e o número de anos para
completar o ensino médio (variável M ) têm distribuição conjunta dada por:
(F, M )
(8,3)
(8,4)
(8,5)
(9,3)
(9,4)
(9,5)
(10,4)
(10,5)
Total
p(f, m)
3/10
1/10
1/10
2/10
1/20
1/10
1/10
1/20
1
Suponha agora que exista o interesse em estudar as variáveis F + M e F.M .
Para isto, podemos acrescentar, à tabela anterior, algumas colunas correspondentes
aos valores dessas novas variáveis. Vejamos:
(F, M )
(8,3)
(8,4)
(8,5)
(9,3)
(9,4)
(9,5)
(10,4)
(10,5)
p(f, m) F + M
3/10
1/10
1/10
2/10
1/20
1/10
1/10
1/20
F.M
7.2. VARIÁVEIS ALEATÓRIAS DISCRETAS
79
Através dessa tabela podemos construir a distribuição da variável Z = F + M e
W = F.M , para isso basta somar as probabilidades nos valores comuns, por exemplo:
P (Z = 13) = P (8, 5) + P (9, 4) =
1
3
1
+
= .
10 20
20
Procedendo de modo similar com os outros valores obtemos as funções de probabilidade de Z e de W :
Z=z
11
P (Z = z)
W =w
P (W = w)
7.2.6
24
12
27
13
32
14
36
15
40
45
50
Esperança de uma função de duas variáveis aleatórias
Um resultado que pode ser bastante útil por não ser necessário obter a distribuição de
uma nova variável que é função de duas variáveis para assim obter o valor esperado é
dado pelo seguinte Teorema.
Teorema 7.2.1. Se X for uma v.a. com valores x1 , . . . , xn e probabilidades p(x1 ), . . . , p(xn ),
Y for uma v.a. com valores y1 , . . . , ym e probabilidades p(y1 ), . . . , p(ym ), se p(xi , yj ) =
P (X = xi , Y = yj ), i = 1, . . . , n, j = 1, . . . , m, e se g(X, Y ) for uma função de X e Y ,
então
n X
m
X
E[g(X, Y )] =
g(xi , yj )p(xi , yj )
i=1 j=1
Este Teorema é diretamente aplicável para o caso de duas variáveis contínuas, além
de mais de duas variáveis(variável multivariada). Este Teorema é uma extensão direta
do Teorema 3.3.1 o qual é aplicado ao caso de uma função de uma única variável.
7.2.7
Medida de Correlação entre duas Variáveis
Quando as variáveis não são independentes isto quer dizer que existe uma certa relação
entre as variáveis. Esta relação pode ser de qualquer tipo, como por exemplo uma
relação linear, quadrática, exponencial, etc. Nosso objetivo aqui não será o de determinar qual o tipo de relação que existe entre as variáveis em questão e sim o de medir
o grau de correlação entre as variáveis. Neste curso iremos medir o grau de correlação
linear entre variáveis quantitativas discretas. Na literatura existem outras medidas de
correlação, inclusive entre variáveis qualitativas, porém este não será o nosso objetivo
neste curso.
80
CAPÍTULO 7. VARIÁVEIS ALEATÓRIAS BIDIMENSIONAIS
Antes de definirmos a medida de correlação linear entre as variáveis vamos enunciar
algumas propriedades envolvendo o valor esperado de funções de variáveis aleatórias.
Propriedade 1: Para variáveis aleatórias X e Y , vale sempre que
E(X + Y ) = E(X) + E(Y ).
No caso do produto de duas variáveis aleatórias nem sempre é válido que o valor
esperado do produto é o produto dos valores esperados. Neste caso temos o seguinte
resultado:
Propriedade 2: Se X e Y são duas variáveis aleatórias independentes, então
E(XY ) = E(X)E(Y ).
Obs: A recíproca desta propriedade não é verdadeira, ou seja, se
E(XY ) = E(X)E(Y ),
então não necessariamente é verdade que X e Y são independentes, a não ser que a
distribuição bidimensional seja a normal.
Provas: Utilize o Teorema 7.2.1.
Exemplo 7.2.6. Considere as variáveis X e Y tendo distribuição conjunta dada por:
X|Y
-1
0
1
2
3
4
2/12
0
3/12
0
1/12 1/12
1/12 2/12 2/12
Calcule, E(X), E(Y ) e E(XY ). Depois determine se X e Y são independentes.
Definição 7.2.6. Uma medida de dependência linear entre X e Y é dada pela covariância:
Cov(X, Y ) = E[(X − E(X))(Y − E(Y ))].
Em palavras, a covariância é o valor esperado do produto dos desvios de cada
variável em relação à sua média.
Desenvolvendo a equação acima chegaremos em uma definição mais usual, que é
dada pela seguinte expressão:
Cov(X, Y ) = E(XY ) − E(X)E(Y ).
Observe que, se X e Y são independentes, então a Cov(X, Y ) = 0; mas a recíproca
nem sempre é verdadeira.
A partir da covariância, definimos uma nova medida de dependência linear.
7.2. VARIÁVEIS ALEATÓRIAS DISCRETAS
81
Definição 7.2.7 (Coeficiente de correlação linear). O coeficiente de correlação
linear entre as variáveis aleatórias X e Y é calculado pela seguinte expressão:
ρX,Y =
Cov(X, Y )
.
σX σY
Onde, σX e σY são respectivamente os desvios-padrão das variáveis X e Y .
A divisão pelo produto dos desvios-padrão, tem a função de padronizar a medida
e tornar possível a comparação com outras variáveis. Pode-se mostrar que |ρX,Y | ≤ 1.
A interpretação de sua expressão segue os mesmos passos da covariância, sendo que
valores de ρX,Y próximos de ±1 indicam correlação forte.
Propriedade 3: Sejam X e Y variáveis aleatórias quaisquer, então
V ar(X + Y ) = V ar(X) + V ar(Y ) + 2Cov(X, Y ).
Se X e Y são independentes, então
V ar(X + Y ) = V ar(X) + V ar(Y ).
Exemplo 7.2.7. Calcule a Cov(F, M ) e ρF,M onde F e M são as variáveis aleatórias
encontradas no Exemplo 7.2.5
82
CAPÍTULO 7. VARIÁVEIS ALEATÓRIAS BIDIMENSIONAIS
7.2.8
Exercícios
1 - O setor de emergência de um pronto socorro infantil anotou o número de crianças
atendidas (C), de médicos (M) e de auxiliares (A) de plantão em 15 dias de
atividades. Os dados são apresentados na tabela abaixo:
Dia
C
M
A
1
5
1
4
2
7
1
4
3
5
2
5
4
6
2
6
5
5
2
7
6
5
1
7
7
7
2
6
8
5
1
5
9 10 11 12 13 14 15
6 6 7 5 5 6 6
1 2 2 2 2 2 2
5 6 7 7 6 6 7
a) Determine as tabelas de freqüência marginais de C, M e A.
b) Obtenha a tabela de freqüência conjunta entre (C, M), (C, A) e (M, A).
c) Calcule a média das variáveis M e A.
2 - Para famílias de um certo bairro de São Paulo, apresentamos abaixo a tabela de
freqüência conjunta das variáveis: número de automóveis (A) e de TVs (T).
A\ T
0
1
2
total
0
1
2 total
110 235 120 465
51 122 178 351
15 84 162 261
176 441 460 1077
a) Calcule as marginais de A e T.
b) Determine as médias destas variáveis.
3 - Uma moeda equilibrada é lançada duas vezes de forma independente. Ao final
dos lançamentos, duas variáveis aleatórias são anotadas: o número total de caras
(C) e o número de coroas no 2ž lançamento (K).
a) Construa uma tabela com a distribuição conjunta das variáveis C e K.
b) Determine o valor esperado de C.
4 - A função conjunta de probabilidade entre as variáveis X e Y é apresentada abaixo
(com algumas entradas faltando):
X\ Y
-2
-1
1
2
P (Y )
0
2
4
P (X)
3/64 1/32
5/16
1/16 1/16
0
1/64 11/64
1/64 5/16
5/64
3/64 1/32
5/16
1/4
1
-1
a) Complete a tabela.
b) X e Y são independentes?
c) Obtenha as marginais de X e Y.
7.2. VARIÁVEIS ALEATÓRIAS DISCRETAS
83
d) Calcule a distribuição da variável W = XY.
e) Calcule ρ(X, Y ).
5 - A função de probabilidade conjunta entre as variáveis aleatórias X e Y é apresentada na tabela abaixo:
X\ Y -2
0
2
4
-1
0,1 0,2 0,1 0,2
1
0,2 0 0,1 0,1
a) Obtenha as distribuições marginais de X e Y.
b) X e Y são independentes?
c) Calcule ρ(X, Y ).
6 - Na caixa I existem duas bolas numeradas 0 e 1, enquanto que a caixa II contêm
duas bolas numeradas -1 e 0. Uma bola é retirada aleatoriamente de cada caixa,
de forma independente uma da outra. A esse experimento, associamos as variáveis
aleatórias: número da bola retirada na caixa I (X), soma dos valores das duas
bolas retiradas (Y ) e a diferença, em módulo, desses valores (Z).
a) Determine a distribuição de probabilidade conjunta entre Xe Y e entre Y e Z.
b) Verifique se Xe Y são independentes. Idem para Y e Z.
c) Calcule a Cov(X, Y ) .
d) Obtenha V ar (X + Y ) .
7 - A variável X é Bernoulli com p = 0, 4 e Y : b(3 : 0, 5). Admita que X e Y são
independentes.
a) Determine P (X = 0 | Y = 2) .
b) Obtenha a distribuição conjunta de Xe Y e do produto W = XY.
c) Calcule E (X) , E (Y ) e E (W ) e verifique que E (W ) = E (X) E (Y ) .
d) Determine o valor de Cov(X, Y ) e ρ (X, Y ) .
84
CAPÍTULO 7. VARIÁVEIS ALEATÓRIAS BIDIMENSIONAIS
7.3
Variáveis Aleatórias Contínuas
Veremos nesta seção o caso em que as duas variáveis aleatórias são contínuas.
7.3.1
Função Densidade Conjunta
Definição 7.3.1 (Densidade conjunta). No caso de duas variáveis aleatórias contínuas, a distribuição conjunta das duas variáveis é caracterizada por uma função f (x, y),
chamada função densidade conjunta de X e Y , satisfazendo:
(a) f (x, y) ≥ 0, para todo par (x, y);
R∞ R∞
(b) −∞ −∞ f (x, y)dxdy = 1;
RbRd
(c) P (a ≤ X ≤ b, c ≤ Y ≤ d) = a c f (x, y)dydx
7.3.2
Densidades Marginais
De maneira análoga ao caso de duas variáveis discretas, temos que as densidades marginais de X e Y são dadas por:
Definição 7.3.2 (Densidades marginais). Dada a v.a. bidimensional (X, Y ), com
função densidade de probabilidade conjunta f (x, y), definimos as densidades marginais
de X e Y respectivamente por
Z ∞
f (x, y)dy
(7.1)
fX (x) =
−∞
e
Z
∞
f (x, y)dx
fY (y) =
(7.2)
−∞
7.3.3
Independência
Definição 7.3.3 (Independência). As variáveis aleatórias X e Y , com densidade
conjunta f (x, y) e marginais fX (x) e fY (y), respectivamente, são independentes se
f (x, y) = fX (x)fY (y), para todo par (x, y).
As definições de covariância, coeficiente de correlação etc. continuam válidas para
o caso de v.a. bidimensionais contínuas. Portanto, se X e Y são independentes, o
coeficiente de correlação entre elas é zero, apesar da recíproca só ser válida se a função
densidade conjunta for de uma distribuição normal.
7.3. VARIÁVEIS ALEATÓRIAS CONTÍNUAS
7.3.4
85
Distribuições Condicionais
Definição 7.3.4 (Distribuições condicionais). A densidade condicional de X,
dado que Y = y é definida por
fX|Y (x|y) =
f (x, y)
,
fY (y)
fY (y) > 0,
e a densidade condicionalde Y , dado que X = x é definida por
fY |X (y|x) =
f (x, y)
,
fX (x)
fX (x) > 0,
Exemplo 7.3.1. Suponha que a densidadede (X, Y ) seja dada por
f (x, y) = 6(1 − x − y),
0 < x < 1,
0<y <1−x
O domínio de variação dos pares (x, y) é um triângulo.
Obtenha as densidades marginais e condicionais. (Obs. esboce um gráfico para
visualizar a variação das variáveis uma em função da outra).
Definição 7.3.5 (Esperança Condicional). A esperança condicional de Y , dado
que X = x, é definida por
Z
∞
E(Y |x) =
yfY |X (y|x)dy
−∞
e definição análoga vale para E(X|y).
7.3.5
Função de Variáveis Aleatórias Contínuas
Neste curso não há tempo hábil para o estudo sobre como obter uma distribuição de
uma v.a. que é função de duas variáveis aleatórias. No livro do Bussab & Morettin,
seção 8.7 (pág. 224) há uma breve descrição sobre este assunto.
86
CAPÍTULO 7. VARIÁVEIS ALEATÓRIAS BIDIMENSIONAIS
7.3.6
Exercícios
1. Para que valor de k a expressão f (x, y) = ke−(x+y) é a f.d.p. conjunta de (X, Y ),
sobre a região 0 < x < 1, 0 < y < 1?
2. Suponha que a f.d.p. conjunta de (X, Y ) seja dada por:
f (x, y) =
e−(x+y) ,
0, c.c.
x > 0, y > 0
a) Ache a f.d.p. marginal de X.
b) Ache a f.d.p. marginal de Y .
c) Verifique se as variáveis X e Y são independentes.
d) Determine as f.d.p.’s condicionadas de X e Y .
e) Calcule P (0 < X < 1, 2 < Y < 5).
f) Calcule P (0 < Y < 1).
g) Calcule P (0 < X < 34 |Y ≤
1
)
3
e P (0 < Y < 34 |X ≤
1
)
3
h) Calcule o coeficiente de correlação ρX,Y .
3. Dada a seguinte f.d.p. conjunta de (X, Y ):
f (x, y) =
3x2 y + 3y 2 x,
0, c.c.
0 < x < 1, 0 < y < 1
a) Ache as f.d.p.’s marginais de X e Y
b) Calcule P ( 21 < X < 34 , 0 < Y < 21 ).
c) Calcule P ( 21 < X < 34 ).
d) Verifique se as variáveis X e Y são independentes.
e) Determine as f.d.p.’s condicionadas de X e Y .
f) Calcule ρX,Y e classifique a dependência entre X e Y , caso haja.
4. Suponha que a f.d.p. conjunta de (X, Y ) seja dada por:
f (x, y) =
x + y, 0 < x < 1, 0 < y < 1
0, c.c.
a) Encontre as f.d.p.’s marginais de X e Y
b) Verifique se as variáveis X e Y são independentes.
c) Calcule P (0 < X < 34 , Y ≤ 13 ).
d) Calcule P (0 < X < 1, Y ≤ 21 ).
e) Calcule P (0 < X < 13 , −1 ≤ Y ≤ 2).
7.3. VARIÁVEIS ALEATÓRIAS CONTÍNUAS
f) Calcule P (0 < X < 31 , 2 ≤ Y ≤ 3).
g) Calcule P (0 < X < 34 |Y ≤ 13 ).
h) Calcule ρX,Y e classifique a dependência entre X e Y , caso haja.
5. Dada a seguinte f.d.p. conjunta de (X, Y ):
c(x2 + y 2 ), 0 < x < 1, 0 < y < 1
f (x, y) =
0, c.c.
a) Determine o valor da constante c.
b) Encontre as f.d.p.’s marginais de X e Y .
c) Verifique se as variáveis X e Y são independentes.
d) Calcule P ( 41 < X < 34 )
e) Calcule P (Y < 21 )
f) Calcule ρX,Y e classifique a dependência entre X e Y , caso haja.
Gabarito:
1. k =
2.
1
(1−e−1 )2
.
a) g(x) = e−x , x > 0
b) h(y) = e−y , y > 0
c) X e Y são independentes.
d) g(x|y) = e−x , x > 0 e h(y|x) = e−y , y > 0
e) 0,081
f) 0,632
g) 0,528 e 0,528
h) Zero
3.
a) g(x) = 23 x2 + x, 0 < x < 1 e h(y) = 23 y 2 + y, 0 < y < 1
b)
c)
29
512
39
128
ou 0,057
ou 0,305
d) X e Y não são independentes.
e) g(x|y) =
4.
6x2 +6xy
3y+2
e h(y|x) =
6y 2 +6xy
3x+2
a) g(x) = x + 12 , 0 < x < 1 e h(y) = y + 21 , 0 < y < 1
b) X e Y não são independentes
c)
d)
e)
13
ou 0,135
96
3
ou 0,375
8
2
ou 0,222
9
87
88
CAPÍTULO 7. VARIÁVEIS ALEATÓRIAS BIDIMENSIONAIS
f) 0
g)
5.
39
64
ou 0,609
a) c =
3
2
b) g(x) =
3x2
2
+ 12 , 0 < x < 1 e h(y) =
c) X e Y não são independentes.
d)
e)
29
64
5
16
ou 0,453
ou 0,3125
3y 2
2
+ 12 , 0 < y < 1
Capítulo 8
Relação de Exercícios
Livro: "Estatística Básica". Wilton O. Bussab e Pedro A. Morettin. 5a. Edicão.
Capítulo 6 (Modelos de variáveis aleatórias discretas):
Problema Página
22, 23 e 24
152
32 e 34
157
37
158
40
159
51
160
Capítulo 7 (Modelos de variáveis aleatórias contínuas):
Problema Página
13
182
19 e 20
183
35
195
40
196
Capítulo 8 (Variáveis aleatórias multidimensionais - caso discreto e bidimensional):
Problema Página
2e3
206
4e5
209
10
210
13
215
17
216
89
90
CAPÍTULO 8. RELAÇÃO DE EXERCÍCIOS
EXERCÍCIOS EXTRAS
1 - Por engano 3 peças defeituosas foram misturadas com peças boas formando um
lote de 12 peças no total. Escolhendo, ao acaso, 4 dessas peças, determine a
probabilidade de encontrar:
a) Pelo menos 2 defeituosas.
b) No máximo 1 defeituosa.
c) No mínimo uma boa.
2 - Em um estudo sobre o crescimento de jacarés, uma pequena lagoa contém 4
exemplares da espécie A e 5 da espécie B. A evolução de peso e tamanho dos 9
jacarés da lagoa é acompanhada pelos pesquisadores através de capturas periódicas. Determine a probabilidade de, em três jacarés capturados, obtermos:
a) Todos da espécie A.
b) Nem todos serem da espécie B.
c) A maioria ser da espécie A.
3 - Admite-se que uma pane pode ocorrer em qualquer ponto de uma rede elétrica
de 10 quilômetros.
a) Qual é a probabilidade da pane ocorrer nos primeiros 500 metros? E de
ocorrer nos 3 quilômetros centrais da rede?
b) O custo de reparo da rede depende da distância do centro de serviço ao local
da pane. Considere que o centro de serviço está na origem da rede e que o
custo é de R$ 200 para distâncias até 3 quilômetros, de R$ 400 entre 3 e 8
quilômetros e de R$ 1.000 para distâncias acima de 8 quilômetros. Qual é
o custo médio do conserto?
4 - Suponha que o valor esperado de uma variável aleatória com distribuição Uniforme contínua é igual a 1 e a variância é 1/12. Encontre a probabilidade da
variável assumir valores menores que 3/4.
5 - O tempo necessário para um medicamento contra dor fazer efeito foi modelado
de acordo com a densidade Uniforme no intervalo de 5 a 15 minutos, tendo por
base experimentos conduzidos em animais. Um paciente, que esteja sofrendo dor,
recebe o remédio e, supondo válido o modelo mencionado acima, pergunta-se a
probabilidade da dor:
a) Cessar em até 10 minutos?
b) Demorar pelo menos 12 minutos?
c) Durar mais de 7 minutos, sabendo-se que durou menos de 10?
6 - O tempo, em minutos, de utilização de um caixa eletrônico por clientes de um
certo banco, foi modelado por uma variável aleatória T com distribuição Exponencial cuja média é igual a 1/3. Determine:
91
a) P(T < 1).
b) P(T > 1 | T > 2).
c) Um número a tal que P(T < a) = 0,4.
7 - Para uma variável aleatória com distribuição Exponencial de parâmetro igual a
1, determine a probabilidade de sorteamos um valor que se distancie no máximo
0,5 da média.
92
CAPÍTULO 8. RELAÇÃO DE EXERCÍCIOS
Parte I
ANEXO
Tabelas
93