Capítulo 3: Fenómenos de superfície - Moodle

16/03/2016
Módulo Física dos Materiais II
2015-2016 (2º Semestre)
Unidade Curricular QUÍMICA E
FÍSICA DOS MATERIAIS II
Programa
3. Fenómenos de superfície
•
•
•
•
•
•
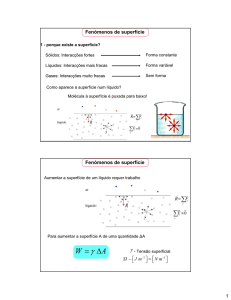
Tensão superficial
Formação de meniscos
Ângulo de contacto
Capilaridade
Equação de Young-Laplace
Fenómenos de transporte: difusão e osmose
1
16/03/2016
Tensão superficial
O fenómeno da
tensão superficial
faz com que a
superfície de um
líquido se
comporte como
uma membrana.
3
Tensão superficial

A força total sobre a
molécula A é nula.


É puxada de igual forma
em todas as direcções.
A força total sobre a
molécula B não é nula.

Não tem moléculas acima.
4
2
16/03/2016
Tensão superficial



O efeito efectivo da
resultante destas forças
em todas as moléculas da
superfície do líquido faz com
que o líquido se contraia.
A superfície tende a adquirir
a menor área possível.
Exemplo: As gotas de água
tomam a forma esférica visto a
esfera apresentar a menor razão
superfície/volume.
5
Tensão superficial sobre uma agulha



A tensão superficial
permite que uma agulha
de aço flutue embora a
sua densidade seja muito
maior que a da água.
A agulha provoca uma
pequena depressão na
superfície do líquido.
As componentes verticais
das forças exercidas pelo
líquido contrabalançam o
peso da agulha.
6
3
16/03/2016
Caminhando sobre a água
F  γL
Força total exercida de cada lado
da pata do insecto
Admitindo que a ponta da pata do insecto
é semi-esférica
Fv  γ2πr  cosθ
perímetro da
extremidade da pata
Fv
Componente vertical da
força F
Fig. 9-42b, p.299
mg
7
Equação da tensão superficial

A tensão superficial é definida como a
razão entre a intensidade das forças
exercidas pela superfície do líquido
(interface) e o comprimento ao longo da
qual são exercidas.
F
γ
L

ou

Ftot
L tot
no caso de existirem várias interfaces.
Unidade SI: N/m
8
4
16/03/2016
Tensão superficial em termos de energia

As unidades da tensão superficial
podem escrever-se em termos de
energia por unidade de área.
γ

N N m
J

 2
m m m m
Um sistema está em equilíbrio quando a
sua energia é mínima.
9
Medição da tensão superficial

A força é medida quando o
anel se liberta do líquido.


Ftot
L tot
A força F é a força exercida
descontado o peso do anel.
10
5
16/03/2016
Tensão superficial: efeito da temperatura
e da adição de surfatantes


A tensão superficial dos líquidos diminui
com o aumento da temperatura.
A tensão superficial pode diminuir por
acção de substancias adicionadas ao
líquido e que se chamam surfatantes.

O detergente é um exemplo de
surfatante.
11
12
6
16/03/2016
Um olhar mais próximo s/ a superfície
dos líquidos: adesão e coesão
Água
Mercúrio
13
Fenómenos de Capilaridade:
Formação de meniscos

A forma dos meniscos
depende:



Mesmo líquido; tubos
de materiais diferentes
das forças de coesão interiores
ao líquido
das forças de adesão entre o
líquido e as paredes dos
contentores
Surgem fenómenos de
capilaridade que resultam
na subida/descida do líquido
pelos contentores (poros)
14
7
16/03/2016
Fenómenos de Capilaridade:
Formação de meniscos

A forma dos meniscos
depende:



Líquidos diferentes; tubos
do mesmo material
das forças de coesão interiores
ao líquido
das forças de adesão entre o
líquido e as paredes dos
contentores
Surgem fenómenos de
capilaridade que resultam
na subida/descida do líquido
pelos contentores (poros)
15
Exemplos de fenómenos de Capilaridade

Infiltração da agua em estruturas verticais:
A água sobe pela estrutura devido à existência de capilares no
interior da estrutura do tijolo.
16
8
16/03/2016
Exemplos de fenómenos de Capilaridade

Infiltração da agua em estruturas verticais:
A água sobe pela estrutura devido
à existência de capilares no
interior da estrutura do tijolo.
É um problema bem conhecido na
edificação de estruturas. Requer
isolamento e materiais resistentes
às infiltrações
17
Exemplos de fenómenos de Capilaridade

Infiltração da água em frescos e pinturas:
A água penetras
nos materiais
(telas, pigmentos,
etc) também por
fenómenos de
capilaridade
18
9
16/03/2016
Exemplos de fenómenos de Capilaridade

Capilaridade em vasos sanguíneos:
Os fenómenos de capilaridade auxiliam a circulação sanguínea
nos vasos capilares do nosso sistema circulatório
19
Exemplos de fenómenos de Capilaridade

Transporte de seiva bruta nas plantas:
Um dos mecanismos de
transporte de água e
nutrientes nas plantas
ocorre justamente por
fenómenos de capilaridade!
20
10
16/03/2016
Fenómenos de Capilaridade: Forças
de adesão e de coesão



Chamam-se forças de coesão (ou coesivas)
às forças entre as moléculas do líquido.
Chamam-se forças de adesão (ou adesivas)
às forças entre as moléculas do líquido e, por
exemplo, as do contentor (forças entre
moléculas diferentes).
A forma da superfície de contacto entre o
líquido e um meio exterior depende da relação
entre essas forças.
21
Superfície de contacto Líquido-Sólido:
caso 1

No caso em que as
forças adesivas são
superiores às forças
de coesão:


O líquido sobe pelas
paredes do contentor.
Diz-se que o líquido
molha a superfície
de contacto.
22
11
16/03/2016
Superfície de contacto Líquido-Sólido:
caso 2

Se as forças de coesão
são superiores às
forças adesivas:


O líquido encurva para
baixo na interface
Diz-se que o líquido
não molha a
superfície de
contacto.
23
Capilaridade



É o fenómeno que resulta
do jogo entre as forças de
tensão superficial e as
forças adesivas.
O líquido sobe no tubo
quando as forças adesivas
são maiores que as forças
de coesão.
Na linha de contacto entre o
líquido e a superfície, as
forças resultantes apontam
para cima.
24
12
16/03/2016
Altura de subida no tubo
F = γL = γ 2 πr 
F v = γ 2 πr  cos 
 Intensidade da força de tensão/adesão
P = mg = ρVg = ρgπr 2 h
 Componente vertical da força
 Peso da coluna de líquido
Condição de equilíbrio: Se a coluna está em
equilíbrio, o peso é equilibrado pela componente
vertical das forças de tensão/adesão:
P = Fv
h=

Fv
ρgπr2h = γ2πr cos 
2γ
cos 
ρgr
φ é o angulo de
contacto entre o liquido
e a parede do recipiente.
25
Capilaridade em acção


Quando as forças de
adesão são menores
que as forças de
coesão, o líquido
desce no tubo.
As forças resultantes
apontam para baixo
neste caso.
26
13
16/03/2016
Capilaridade em acção
Pressão diferencial na zona do menisco (lei
fundamental da hidrostática):
p = ρ gh
Força de pressão exercida no sentido ascendente:
FP =pA=  gh   r 2 
Componente vertical da força de
tensão/adesão:
F v = γ 2 πr  cos 
Equilíbrio:
FP = Fv

h=
2γ
cos
ρgr
A profundidade é dada pela
mesma expressão.
27
Ângulo de contacto:
28
14
16/03/2016
Ângulo de contacto: adesão e coesão


Se o ângulo de
contacto, Φ < 90°, as
forças adesivas são
maiores que as
forças de coesão.
Se o ângulo de
contacto, Φ > 90°, as
forças de coesão são
maiores que as
forças adesivas.
Efeito Lotus
29
Molhabilidade de superfícies
A molhabilidade (wetting) de uma superfície está
relacionada com o ângulo de contacto. Quanto maior o
ângulo de contacto menos molhável é a superfície
Má molhabilidade
Φ>90º
boa molhabilidade
Φ<90º
Molhabilidade
Completa Φ=0º
Superfície hidrófobas:
São superfícies com baixa
(má) molhabilidade
Superfícies hidrófilas:
são superfícies com boa
molhabilidade ou
molhabilidade completa
30
15
16/03/2016
Ângulo de contacto, molhabilidade e balaço entre forças
de Adesão / Coesão
Em resumo, temos as seguintes relações entre o ângulo de
contacto, molhabilidade e balanço entre as forças de adesão
coesão
ÂNGULO DE
CONTACTO
(em graus)
GRAU DE
MOLHABILIDADE
φ=0
Molhabilidade
completa
0<φ<90
Molhabilidade
elevada
90≤φ<180
Baixa
molhabilidade
φ=180
Molhabilidade
nulas
FORÇAS DE
ADESÃO
(interacções sólido
líquido)
FORÇAS DE
COESÃO
(interacções
líquido - liquido)
Fortes
Fracas
Muito fortes
Muito fracas
Médias
Médias
Muito fracas
Muito Fortes
Fracas
Fortes
31
A equação de Young-Laplace
A forma de uma gotícula resulta do balanço de forças de
pressão interiores e exteriores à superfície de contacto
líquido – gas e da tensão superficial da gota.
Este balanço é descrito pela
equação de Young –
Laplace:
1 1
p     
 r 1 r2 
gas
líquido
onde r1 e r2 são os raios de
curvatura da gotícula, γ, é a
tensão superficial, e
p  plíquido  pgas
32
16
16/03/2016
A equação de Young-Laplace
A equação de Young-Laplace permite determinar experimentalmente
a tensão superficial dos líquidos, através do método da gotícula
pendente. Este método consiste em medir os raios (r1 e r2) de
curvatura de uma gota pendente e determinar a deformação da gota
para calcular a pressão diferencial Δp=ρgh

p
1/r1  1/ r2
33
TL2: Ângulos de contacto, molhabilidade e tensão superficial
Objectivos:
• Medição de ângulos de contacto de gotículas de água em superfícies com diferentes graus
de molhabilidade.
• Descrição qualitativa do grau de molhabilidade de superfícies.
• Cálculo da capacidade de infiltração da água em capilares de diferentes materiais.
Material:
• Equipamento de medida de ângulos de contacto DSA30 (Kruss, Germany)
•Amostras de materiais de diferentes graus de molhabilidade;
• Programa de analise de imagens Drop Shape Analyser DAS30;
• Água milipore; Transferidor.
34
17
16/03/2016
TL2: Ângulos de contacto, molhabilidade e tensão superficial
Descrição experimental:
Os estudos de molhabilidade das superfícies a analisar serão realizados através da medição de
ângulos de contacto estático a realizar de forma manual e automática. O método manual consiste
na medição dos ângulos de contacto com transferidor sobre imagens em formato bmp recolhidas
com o equipamento DAS30 (ver figura abaixo). A medição automática é feita pelo software do
equipamento de análise de imagem, através do método da gota séssil.
Relatório/questionário:
• Determinação automática e manual de ângulos de contacto
• Cálculo da capacidade de infiltração da água em capilares ;
• Interpretação dos fenómenos de adesão, coesão e tensão superfícial;
• Descrição qualitativa do grau de molhabilidade de superfícies.
35
Difusão
A Difusão é um mecanismo físico que consiste na
passagem espontânea de moléculas num meio fluído
para regiões onde a sua concentração é inferior.
Temos por exemplo os casos da difusão de um gás:
Lei de Grahm: razão de velocidades de difusão é dada por:
(v1, v2, ρ1 e ρ2 são as velocidades de difusão e densidades dos meios 1 e 2.
v1
2

v2
1
36
18
16/03/2016
Difusão
A efusão é um mecanismo de difusão através de
superfícies porosas.
Exemplo micro-poros na superfície um balão cheio de ar:
37
Osmose
A Osmose é um mecanismo físico que consiste na
movimentação das moléculas de água de uma solução,
entre regiões separadas por uma membrana
semipermeável.
A água movimenta-se das regiões onde a concentração
de soluto é menor (meio hipotónico) para regiões onde
a concentração de soluto é maior (meio hipertónico),
na tentativa de igualar as concertações de soluto.
38
19