W = γ ∆A

Fenómenos de superfície
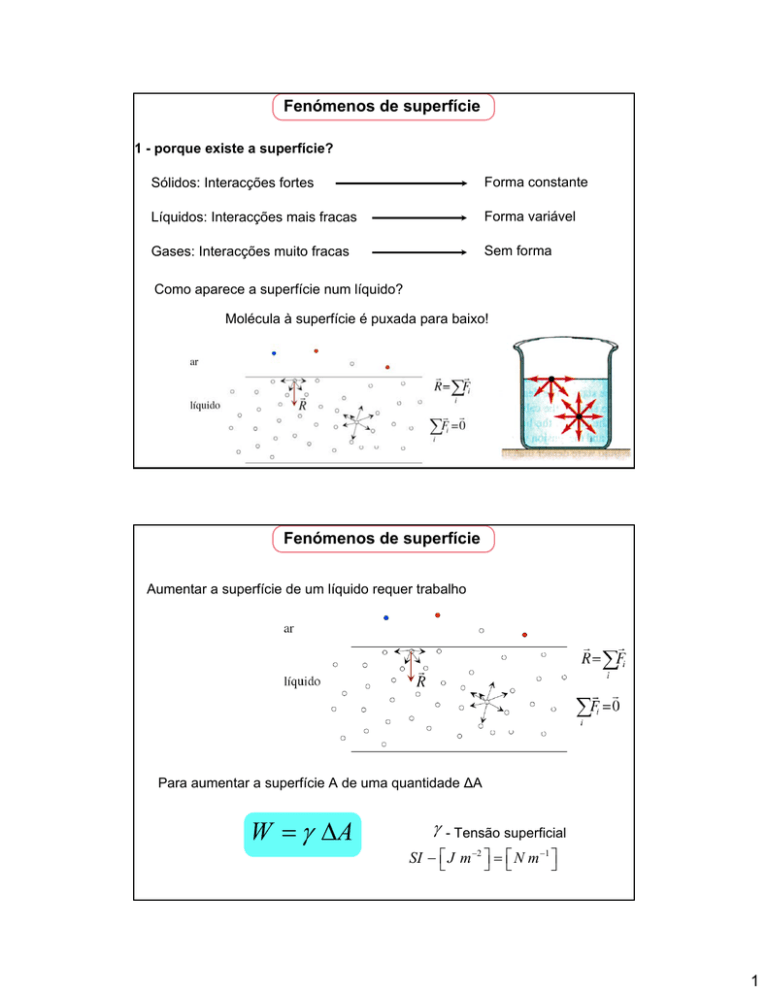
1 - porque existe a superfície?
Sólidos: Interacções fortes
Forma constante
Líquidos: Interacções mais fracas
Forma variável
Gases: Interacções muito fracas
Sem forma
Como aparece a superfície num líquido?
Molécula à superfície é puxada para baixo!
Fenómenos de superfície
Aumentar a superfície de um líquido requer trabalho
Para aumentar a superfície A de uma quantidade ∆A
W = γ ∆A
γ
- Tensão superficial
SI − ⎡⎣ J m −2 ⎤⎦ = ⎡⎣ N m −1 ⎤⎦
1
Fenómenos de superfície
Energia
potencial
da superfície
2 - Energia de coesão
Se é preciso trabalho para fazer uma superfície
igual ao trabalho realizado para formar a superfície
de
W = γ ∆A
Energia
de Gibbs
da superfície
Energia ∝ área total da superfície
Fenómenos de superfície
A Energia de Coesão (Energia de Gibbs de Superfície):
Energia mínima para romper uma coluna líquida com área unitária
γ - Energia para aumentar área 1 unidade
Energ. Gibbs = 2
γ
2
Fenómenos de superfície
3 - Tensão Superficial
Força tangente à superfície por
unidade de comprimento
F
γ =
2l
Porque atribuir F à acção das superfícies?
Película ≠ de membrana de borracha!
Experiência
⇒ arame em equilíbrio para qualquer posição
Fenómenos de superfície
Experiência
γ =
arame em equilíbrio para qualquer posição
F
2l
Quando se estica
⇒ moléculas do interior passam para
a superfície
como
F =2f
tensão superficial:
temos
γ =
f
l
força que uma superfície exerce
por unidade de comprimento
3
Fenómenos de superfície
Temos duas definições de tensão superficial:
W = γ ∆A
γ =
f
l
f é a mesma para
qualquer
posição do arame
W = f ∆x = γ ∆A = γ l∆x
Unidades de tensão superficial:
γ =
f
l
⎡⎣ Jm −2 ⎤⎦ ≡ ⎡⎣ Nm −1 ⎤⎦
Fenómenos de superfície
Tensão
Superficial
γ
⎧energia necessária para criar uma área unitária de superfície
⎨força tangencial que a superfície exerce por unidade de comprimento
⎩
4
Fenómenos de superfície
4 - Forças de adesão e de coesão
γ =
gás
f
W
=
∆A l
líquido
Forças de coesão: interacção entre as moléculas do líquido
Forças de adesão: interacção entre as moléculas do líquido e as do meio
em contacto com o líquido
Fronteira líquido—gás:
Forças de coesão >> Forças de adesão
Superfície líquida é
plana
Fronteira líquido—sólido:
Forças de coesão ≈ Forças de adesão
ângulo de contacto
Fenómenos de superfície
ângulo de contacto
⎧Forças de coesão
θ – depende da competição entre ⎨
⎩Forças de adesão
líquido– líquido
líquido– sólido
Forças que superfície do líquido exerce
na parede é tangente à superfície:
Se θ < 90° líquido sobe
Se θ > 90° líquido desce
5
Fenómenos de superfície
5 - Capilaridade
Peso da coluna = força que parede do
tubo exerce na
superfície do líquido
θ < 90°
⎧ Componente horizontal é nula
dF ⎨
⎩Componentes verticais somam-se
ρ
dFvert . = dF cos θ = γ dl cos θ
γ cos θ
Força por unidade
de comprimento
Fvert . = 2π r γ cos θ
⎧ Componente horizontal é nula
dF ⎨
⎩Componentes verticais somam-se
dFvert . = dF cos θ = γ dl cos θ
γ cos θ
Força por unidade
de comprimento
Fvert . = 2π r γ cos θ
Para a coluna de líquido no capilar:
P = π r 2 h ρg
V = π r2h
h=
2 γ cos θ
ρ gr
Lei de Jurin
6
Fenómenos de superfície
Lei de Jurin
h=
2 γ cos θ
ρ gr
h=
2 γ cos θ
ρ gd
L >> d
h L d ρ g = 2 L γ cos θ
Fenómenos de superfície
θ = 0° — líquido “molha” o sólido
θ = 180° — líquido “não molha” o sólido
7
Fenómenos de superfície
QuickTime™ and a
Video decompressor
are needed to see this picture.
Fenómenos de superfície
Um objecto pode fluctuar mesmo que
o seu peso exceda a impulsão máxima
8
Clip a fluctuar numa solução iluminada por luz polarizada
Fenómenos de superfície
Relação entre a diferença de pressão através superfície e
a Tensão superficial e forma da superfície
Lei
de
Laplace
Membrana esférica de raio r, tensão superficial γ
Forças numa metade:
- tensão superficial (2πrγ)
- diferença de pressão (P’-P)
9
- tensão superficial (2πrγ)
- diferença de pressão (P’-P)
Componentes da pressão no plano
⊥ a OZ anulam-se
Componentes no eixo OZ somam-se
dF = ( P ′ − P)dAn̂
dFz = ( P ′ − P)dAn̂ ⋅ k̂
dAn̂ ⋅ k̂
Logo:
Integrada para toda a área dá
π r2
F = ( P ′ − P)π r 2 = 2π rγ
( P ′ − P)π r 2 = 2π rγ
ou
( P ′ − P) = ∆P =
2γ
r
Lei de Laplace para membrana esférica
Para membrana cilíndrica:
( P ′ − P) =
γ
Lei de Laplace para membrana cilíndrica
r
Bola de sabão: é uma película de líquido - 2 superfícies = 2 tensões superficiais
Como os dois raios de curvatura são ~ iguais
( P ′ − P) =
4γ
r
Lei de Laplace para película de líquido esférica
10
No caso mais geral de uma superfície qualquer:
r1 e r2
são os raios de curvatura máximo e mínimo
Demonstra-se:
⎛ 1 1⎞
( P ′ − P) = γ ⎜ + ⎟
⎝ r1 r2 ⎠
Membrana esférica:
Membrana cilíndrica:
Película esférica:
r1 = r2 = r
r1 = ∞ e r2 = r
r1 = r2 = r
e 2 superfícies
Planos principais
Lei de Laplace
2γ
r
γ
( P ′ − P) =
r
4γ
( P ′ − P) =
r
( P ′ − P) =
Gotas, ou bolhas, em contacto
de
( P ′ − P) =
2γ
r
Como r1 < r2
2γ 2γ
>
r1
r2
P1′ > P2′
Matéria passa da gota pequena para a grande:
evolução é no sentido do desaparecimento das gotas menores
11
Determinação do Ângulo de Contacto e da Tensão Superficial
Tensão superficial
Um método directo
γ =
F
2l
Uma alternativa simples
Lei de Jurin
h=
2 γ cos θ
ρ gr
O problema é que requer o conhecimento simultâneo de θ
Determinação do Ângulo de Contacto
Método da Placa Inclinada
12
Determinação da Tensão Superficial
1 - Método do tubo capilar
γ=
hρ gr
2 cosθ
É preciso conhecer θ - experiência anterior!
2 - Método da Placa de Wilhelmy
13
3 - Outros métodos
a) Método da máxima pressão de bolha — Medida da pressão máxima a
que uma bolha de gás inerte
se liberta de um capilar
mergulhado no líquido.
b) Método do peso de gota —
Gotas do líquido libertadas de
um capilar são recolhidas e
pesadas.
c) Método do anel —
Mede-se a força necessária
para libertar um anel de fio do
líquido.
14
Interfaces entre líquidos imiscíveis
Energia de uma superfície
ES = WS = γ A
Quando temos dois líquidos imiscíveis em contacto
Energia da superfície de interface:
Em que
γ 12
ES12 = γ 12 A
= W12
é a tensão superficial de contacto entre os 2 líquidos
Energia (ou trabalho) de adesão
(por unidade de área)
W12 = γ 1 + γ 2 − γ 12
(aparecem duas superfícies líq-ar
e desaparece uma superf. líq-líq)
Se os líq. forem iguais = 2 Υ
Interfaces entre líquidos imiscíveis
Gota de líquido 2 sobre líq. 1
ar
Para haver equilíbrio na interface
é necessário que as 3 forças se anulem
r r
r
f1 + f2 + f12 = 0
de módulos:
f1 = γ 1l
f2 = γ 2 l
f12 = γ 12 l
15
Interfaces entre líquidos imiscíveis
ar
Se o ângulo α for muito pequeno:
f1 = f2 + f12
Mas,
f1
pode não ser anulada pelas outras duas forças
camada
monomolecular
Não há equilíbrio e o líquido 2 espalha-se por cima do 1
f1 > f2 + f12
W12 > W2
γ 1 > γ 2 + γ 12
γ 1 + γ 2 − γ 12 > 2γ 2
Energia de
adesão dos
líqs 1-2
Energia de
coesão de Gibbs
do líquido 2
Agentes tensioactivos
São moléculas polares que diminuem a tensão superficial da água
Lípidos
Detergentes
16
Agentes tensioactivos
Como diminuiem a tensão superficial?
Forma-se uma monocamada de moléculas tensioactivas
Agentes tensioactivos
Outros fenómenos associados a estas moléculas:
membranas
“bolas de sabão”
efeito detergente
17