Matemática – 9º ano
Ângulo ao Centro e Ângulo Inscrito numa Circunferência
Arcos e Cordas Correspondentes
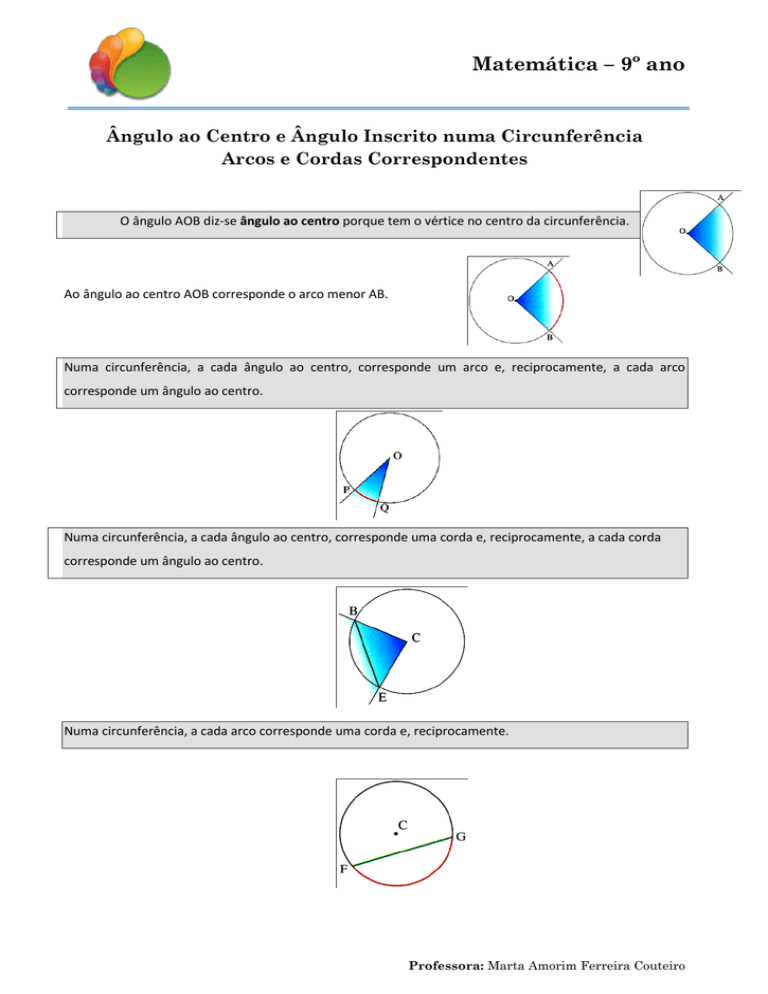
O ângulo AOB diz-se ângulo ao centro porque tem o vértice no centro da circunferência.
Ao ângulo ao centro AOB corresponde o arco menor AB.
Numa circunferência, a cada ângulo ao centro, corresponde um arco e, reciprocamente, a cada arco
corresponde um ângulo ao centro.
Numa circunferência, a cada ângulo ao centro, corresponde uma corda e, reciprocamente, a cada corda
corresponde um ângulo ao centro.
Numa circunferência, a cada arco corresponde uma corda e, reciprocamente.
Professora: Marta Amorim Ferreira Couteiro
Matemática – 9º ano
IGUALDADE DE ARCOS, CORDAS E ÂNGULOS AO CENTRO CORRESPONDENTES
Observa a figura, onde o arco AB é simétrico do arco CE, em relação à reta r.
Então:
♦ O arco AB e o arco CE são geometricamente iguais;
♦ A é simétrico de E;
♦ B é simétrico de C.
Logo,
♦ as cordas [AB] e [CE] são geometricamente iguais.
♦ os ângulos AOB e COE são geometricamente iguais.
Assim,
Numa circunferência, a arcos iguais correspondem cordas e ângulos ao centro iguais.
Numa circunferência, a ângulos ao centro iguais correspondem arcos e cordas iguais.
Numa circunferência, a cordas iguais correspondem arcos e ângulos ao centro iguais.
AMPLITUDE DE UM ARCO DE CIRCUNFERÊNCIA
̂.
A amplitude do arco AB representa-se por 𝑨𝑩
A amplitude de um arco de circunferência é igual à amplitude do ângulo ao centro que lhe corresponde.
EXERCÍCIOS
1. Assinala a outra cor o arco e o ângulo ao centro, correspondente à corda [LM].
2. Na figura seguinte a circunferência tem centro em O.
Indica:
a) um ângulo ao centro.
b) uma corda.
c) uma semicircunferência.
d) uma corda e o arco correspondente.
Professora: Marta Amorim Ferreira Couteiro
Matemática – 9º ano
3. A circunferência tem centro no ponto C e arco GH arco IJ.
a) Justifica que 𝐺𝐶̂ 𝐻 𝐼𝐶̂ 𝐽.
c) Desenha as cordas [GH] e [IJ] e justifica que são iguais.
d) Prova que [GCH] [ICJ].
4. Determina a e b. Explica o teu raciocínio.
O é o centro da circunferência
C é o centro da circunferência
5. A circunferência tem centro O.
̂.
a) Se AÔB = 35º, determina 𝐴𝐵
̂ = 42º, determina AÔB e 𝐴𝐶𝐵
̂.
b) Se 𝐴𝐵
̂ = 300º, determina AÔB.
c) Se 𝐴𝐶𝐵
ÂNGULO INSCRITO NUMA CIRCUNFERÊNCIA
Todos os ângulos representados nestas figuras possuem o vértice sobre a respetiva circunferência e os seus
lados contêm cordas.
Chama-se ângulo inscrito a um ângulo com o vértice sobre a circunferência e em que cada lado contém uma
corda dessa mesma circunferência.
Professora: Marta Amorim Ferreira Couteiro
Matemática – 9º ano
RELAÇÃO ENTRE A MEDIDA DE AMPLITUDE DE UM ÂNGULO INSCRITO E A MEDIDA DE AMPLITUDE DO ARCO COMPREENDIDO
ENTRE OS SEUS LADOS
A amplitude de um ângulo inscrito é igual a metade da amplitude do arco
correspondido entre os seus lados.
EXERCÍCIOS
̂ = 250°.
1. Calcula 𝑋𝑌̂𝑍 sabendo que o 𝑋𝑍
̂.
̂ = 80° calcula 𝐴𝑉𝐵
2. Sendo 𝐴𝑉̂ 𝐶 = 30° e 𝑉𝐵
̂ . Calcula:
̂ = 4 × 𝐴𝑉
3. Na figura, 𝑉𝐵
a) 𝐴𝑉̂ 𝐵
b) 𝑉𝐴̂𝐵
c) 𝐴𝐵̂ 𝑉
Professora: Marta Amorim Ferreira Couteiro