Lógica e Raciocínio - Universidade da Madeira

Lógica e Raciocínio
Universidade da Madeira
http://dme.uma.pt/edu/LeR/
Introdução a Teoria da Decisão
1
Conteúdos
Os tópicos que vamos abordar:
ÎDecisão sob ignorância
Î Decisão sob Risco
ÎTeoria da Probabilidade
ÎFunção de Utilidade
O que são Teoria da Decisão e
Análise da Decisão?
ÎTeoria da Decisão é o resultado de um esforço
conjunto de economistas, matemáticos, filósofos,
sociólogos e estatísticos para explicar como os
indivíduos ou grupos fazem ou devem tomar
decisões. (Resnik, 1987)
ÎOs principais objectivos da Teoria da Decisão são,
primeiramente, fornecer modelos para como nos
guiamos os nossos desejos e as nossas crenças e,
no segundo lugar para esclarecer como combinamse em decisões racionais (Gärdenfors & Sahlin,
1988)
2
O que são Teoria da Decisão e
Análise da Decisão?
ÎUma filosofia, articulada por um conjunto de
axiomas lógicos e uma metodologia e colecção de
procedimentos sistemáticos baseados nestes
axiomas, com o fim de analisar as complexidades
inerentes em problemas da decisão.” (Keeney,
1982)
ÎAnálise da Decisão é o termo utilizado para referir a
cuidadosa deliberação que precede uma decisão
Mas especificamente refere-se aos aspectos
quantitativos desta (French, 1988)
Onde aplica-se teoria da decisão?
ÎFerramentas de análise de risco e decisão
ÎInteligência Artificial
ÎAnalise Operacional
ÎModelos Económicos
ÎGrupos de Decisão
3
Componentes
ÎO problema é analizado desde as
alternativas (actos)
ÎAs alternativas conduzem aos resultados
(prémios, consequências)
ÎEstes são analisados com base num valor v
ou na utilidade u, e a probabilidade p
ÎPodem também ser considerados outros
critérios diferentes (aspectos, perspectivas)
Modelo Base
ÎUma decisão implica uma escolha
entre dois ou mais possíveis
alternativas
ÎCada alternativa leva a um o mais
futuros estados
ÎUm estado conjuntamente com a
alternativa formam uma consequência
4
Exemplo
ÎDecisão: Devo levar o guarda-chuva
ao passeio?
)Alternativas: levo o guarda-chuva, não
levo o guarda-chuva
)Estados: Começa a chover, não começa a
chover
)Consequências: Chove e não tenho
guarda-chuvas, não chove e tenho
guarda-chuva, etc
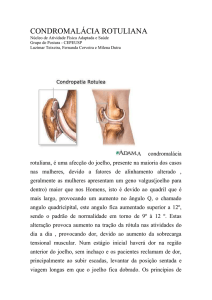
Árvore de Decisão
Î Consiste de quatro componentes
Î Nós de decisão (quadrados)
Î Nós de Probabilidade (círculos)
Î Nós de consequência triângulos
Î Eixos
Probability
node
decisão node
Consequence
node
5
Avaliação das consequências
Analisar os valores ser frequentemente difícil. Necessita
encontrar uma escala para medir as consequências.
ÎComparar Celsius, Fahrenheit, etc. para a temperatura
ÎMais como é possível, por exemplo medir os aspectos do
ambiente (nublado, instável, etc.). Na literatura e no
software convencional são necessários valores precisos
para achar estimações correctas.
Análise de planos de acção (Análise
de cenários )
Investiga que tão provável é cada um dos possíveis
resultados
ÎExaustivo: pelo menos uma das consequências vá
acontecer.
ÎDisjuntivo de a pares: no máximo uma das consequências
vá acontecer.
ÎÆ : exactamente uma das consequências vá acontecer.
Utilizamos probabilidades p com a finalidade de
quantificar as nossas crenças (Σpi = 100%).
6
Avaliação
Mesmo que possuamos conhecimento
acerca de todos os dados de fundo,
precisamos saber como escolher. Aqui
é que a teoria da decisão entra em jogo.
Algumas regras de decisão
ÎPreferência (Dominance)
ÎRegra Maximin/Maximax
ÎRegra de Optimismo – Pessimismo
ÎRegra Minimax Regret
ÎPrincipio da ração insuficiente
ÎEtc.
7
Maximizando a utilidade
esperada
A utilidade esperada e o valor da a media ponderada
Σpxiuxi = px1ux2+px2ux2+...+px(n-1)ux(n-1)+pxnuxn
Alt. 1
u11
p11
p12..
p1n
u12
.
u1n
Alt. 2
u21
p21
p22..
p2m
u22
.
u2m
Escolher a alternativa com a utilidade esperada mais
elevada..
Problema de Decisão : gangrene
Formulação da decisão :
Um paciente de 68 anos tem que escolher entre:
ÎA amputação da perna esquerda por baixo do
joelho.
ÎTratamento com medicamentos
ÎCom a amputação o risco de vida é de 1%
ÎCom o tratamento com medicamentos, a
probabilidade é, num passo posterior, de 30% de
precisar amputar a perna por cima do joelho, com
risco de morrer de 10%
8
Alternativas
As alternativas consistem em escolher o que
fazer, se amputar ou usar medicamentos
Identificando as consequências
As consequencias é o que acontece de acordo com cada
alternativa:
ÎC11: Perna amputada por baixo do joelho, saudável
ÎC12: Morte
ÎC21: saudável
ÎC22: Perna amputada por cima do joelho, saudável
ÎC23: Morte
9
Estruturando o Problema
Distribuição de Probabilidades
ÎC11: Perna amputada por baixo do joelho, saudável
0,99
ÎC12: Morte
0,01
ÎC21: saudável
0,70
ÎC22: Perna amputada por cima do joelho, saudável
0,27
ÎC23: Morte
0,03
10
Actualizamos a Estrutura
Agregamos as Probabilidades
Avaliação. Passo 1
ÎSe o paciente considera a probabilidade de
morrer como um factor determinante, então
deve escolher a amputação.
ÎSe o paciente considera a diferencia
insignificante (0,03 vs. 0,01) e a
possibilidade de ficar completamente
curado é um factor determinante, então deve
escolher a medicação.
11
Avaliação. Passo 2 – Escala de
valores
Aqui podemos considerar
ÎA utilidade da morte é a mais baixa
ÎA utilidade de ficar saudável é a mais alta
Escolhemos uma escala de valores
Îu(morte) = 0
Îu(saudável) = 1
Estimar as consequências
É difícil de quantificar, mas usualmente se utiliza um intervalo ou um
ranking
Valores Precisos:
Î Perna amputada por baixo do joelho = 0.8
Î Perna amputada por cima do joelho = 0.6
Exemplo de Intervalos :
Î Perna amputada por baixo do joelho = [0.7, 0.9].
Î Perna amputada por cima do joelho = [0.5, 0.7].
Ordem de preferência:
Î Perna amputada por baixo do joelho é melhor que Perna amputada por
cima do joelho
12
Estruturando - valores
Inserimos os valores
Utilidade Esperada
A utilidade esperada de cada alternativa:
Î A1(amp.): p(amp. bj)*u(amp. bj) + p(morte)*u(morte)
= 0,99*0,8 + 0,01*0 = 0,792
(probabilidade * utilidade de Perna amputada por baixo do joelho +
probabilidade * utilidade de morte)
Î A2 (medic.): p(saudável)*u(saudável) + p(amp. cj)*u(amp. cj) +
p(morte)*u(morte) = 0,7*1 + 0,27*0,6 + 0,03*0 = 0,862
(probabilidade * utilidade de saudável + probabilidade * utilidade de
Perna amputada por cima do joelho + probabilidade * utilidade de
morte)
13
Consequências Posteriores
Suponhamos que alguns anos depois da
medicação a doença possa voltar:
ÎC211: Saudável nos próximos 5 anos (75%)
ÎC212: Perna amputada por baixo do joelho (7%)
ÎC213: Perna amputada por cima do joelho (15%)
ÎC214: Morte (3%)
Consequências Posteriores
14
Utilidade Esperada
A utilidade esperada de cada alternativa:
ÎA1(amp.): 0,792 (não muda)
ÎA2 (medic.):
0,7*0,75*1+
p(saudável)* p(saudavél 5
nos)*u(saudável) +
0,7*0,07*0.8+p(saudavél)*p(amp. bj)*u(amp. bj) +
0,7*0,15*0.6+p(saudavél)*p(amp. cj)*u(amp. cj) +
0,7*0,03*0+
p(saudavél)*p(morte)*u(morte) +
0,27*0.6+ p(amp. cj)*u(amp. cj) +
0,03*0
p(morte)*u(morte) =
= 0,789
15