UNIVERSIDADE FEDERAL DE OURO PRETO - ICEB-UFOP

UNIVERSIDADE FEDERAL DE OURO PRETO
Disciplina: EST202
Professor: Fernando Luiz Pereira de Oliveira
Lista 6 de exercícios
Atividade 1)
Para realizar uma análise posterior no projeto KP&L, precisamos desenvolver probabilidades
para cada um dos nove resultados experimentais listados na Tabela 1.0. Com base na
experiência e julgamento, a administração concluiu que os resultados experimentais não eram
igualmente prováveis. Portanto, o método clássico de atribuição de probabilidades não
poderia ser usado. A administração decidiu então realizar um estudo de tempos de término
para projetos similares empreendidos pela KP&L nos últimos três anos. Os resultados de um
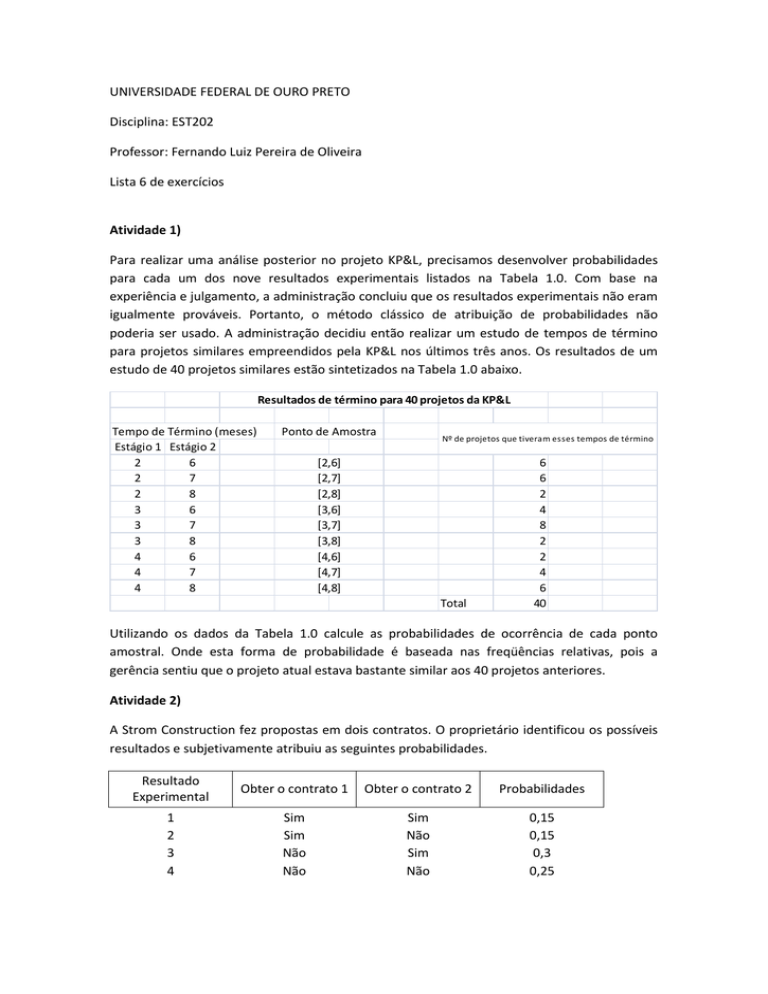
estudo de 40 projetos similares estão sintetizados na Tabela 1.0 abaixo.
Resultados de término para 40 projetos da KP&L
Tempo de Término (meses)
Estágio 1 Estágio 2
2
6
2
7
2
8
3
6
3
7
3
8
4
6
4
7
4
8
Ponto de Amostra
Nº de projetos que tiveram esses tempos de término
[2,6]
[2,7]
[2,8]
[3,6]
[3,7]
[3,8]
[4,6]
[4,7]
[4,8]
Total
6
6
2
4
8
2
2
4
6
40
Utilizando os dados da Tabela 1.0 calcule as probabilidades de ocorrência de cada ponto
amostral. Onde esta forma de probabilidade é baseada nas freqüências relativas, pois a
gerência sentiu que o projeto atual estava bastante similar aos 40 projetos anteriores.
Atividade 2)
A Strom Construction fez propostas em dois contratos. O proprietário identificou os possíveis
resultados e subjetivamente atribuiu as seguintes probabilidades.
Resultado
Experimental
Obter o contrato 1
Obter o contrato 2
Probabilidades
1
2
3
4
Sim
Sim
Não
Não
Sim
Não
Sim
Não
0,15
0,15
0,3
0,25
a) Estas atribuições de probabilidade são válidas? Explique.
b)O que teria de ser feito para tornar válidas as atribuições de probabilidade.
Atividade 3)
Na tabela 1.1 são mostradas as distribuições de freqüência percentual das contagens da
satisfação no trabalho, para uma amostra de executivos seniores de sistemas de informação e
gerentes médios de sistema de informação (Computerworld, 26 de maio de 1997). As
contagens variam de um baixo valor de 1(bastante insatisfeito) até um alto valor de 5(bastante
satisfeito).
a) Desenvolva uma distribuição de probabilidade para a contagem da satisfação de um
executivo sênior no trabalho.
b) Desenvolva uma distribuição de probabilidade para a contagem da satisfação de um gerente
médio no trabalho.
c) Qual é a probabilidade de que um executivo sênior reportará uma contagem de satisfação
de 4 ou de 5 no trabalho?
d) Qual é a probabilidade de um gerente médio estar bastante satisfeito?
e) Compare a satisfação dos executivos seniores e dos gerentes médios no trabalho global.
Tabela 1.1
Contagem de Satisfação no
Trabalho
1
2
3
4
5
Executivos Seniores de
Sistema de Informação
Gerentes Médio de Sistemas
de Informação
5
9
3
42
41
4
10
12
46
28
Atividade 4)
O diretor de admissão do Lakeville Community College avaliou subjetivamente uma
distribuição de probabilidade para x, o número de estudantes que ingressam, como segue:
x
f(x)
1.000
0,15
1.100
0,2
1.200
0,3
1.300
0,25
1.400
0,1
a) Esta é uma distribuição de probabilidade válida?
b) Qual é a probabilidade de que haverá 1.200 estudantes ou menos ingressando?
Atividade 5)
Utilizando a Tabela 1.1.
a) Qual é o valor esperado da contagem da satisfação no trabalho para os executivos seniores?
b) Qual é o valor esperado da contagem da satisfação no trabalho para os gerentes médios?
c) Calcule a variância das contagens de satisfação no trabalho para os executivos e os
gerentes?
d) Calcule a desvio padrão das contagens de satisfação no trabalho para os executivos e os
gerentes?
Atividade 6)
Dica: Se X é uma variável aleatória e a e b são constantes reais, então:
Atividade 7)
A demanda para um produto das indústrias Carolina varia grandemente de mês para mês. A
distribuição de probabilidade na seguinte tabela, baseada nos dados dos últimos dois anos,
mostra a demanda mensal da empresa.
Demanda unitária Probabilidade
300
0,2
400
0,3
500
0,35
600
0,15
a) Se a empresa baseia as ordens de compra mensais no valor esperado da demanda mensal,
qual deve ser a quantidade de ordens de compra mensais da Carolina para esse produto?
b) Considere que cada unidade demandada gera US$70 de receita e que cada unidade
comprada custa US$50. Quanto a empresa ganhará ou perderá em um mês se ela colocar uma
ordem de compra baseada em sua resposta no item (a) e a atual demanda para o item são 300
unidades?
Atividade 8)
Atividade 9)
Seja f uma função de densidade de um determinado fundo de investimento definida por:
f x
2
x 1, x
27
0,
x
a) Mostre que f(x) é uma função de densidade;
b) Calcule:
i) P X 4 ,
ii) P X
as respectivas áreas no gráfico de f(x);
c) Encontre a média e a variância de X.
3 ,
2,5
2,5
iii) P 3
X
4 , mostrando