1
UNIVERSIDADE FEDERAL DO PARANÁ
ELISA BEATRIZ DE ABREU GUIMARÃES
MARIANA TEIXEIRA PINTO NEUMANN
PROGRAMA PARA CÁLCULO DE CURTO-CIRCUITO
CURITIBA
2009
2
ELISA BEATRIZ DE ABREU GUIMARÃES
MARIANA TEIXEIRA PINTO NEUMANN
PROGRAMA PARA CÁLCULO DE CURTO-CIRCUITO
Projeto de Final de Curso apresentado à
Disciplina de Projeto de Graduação como
requisito parcial à conclusão do Curso de
Engenharia Elétrica, Setor de Tecnologia,
Departamento de Engenharia Elétrica,
Universidade Federal do Paraná.
Orientadora: Profa. Dra. Thelma S. Piazza
Fernandes
CURITIBA
2009
3
AGRADECIMENTOS
Aos nossos pais por todos os esforços realizados.
À Profa. Thelma Solange Piazza Fernandes pela orientação e paciência.
A todos os professores do curso de Engenharia Elétrica da Universidade
Federal do Paraná pelos ensinamentos transmitidos.
4
RESUMO
Este trabalho tem como objetivo desenvolver um programa computacional para
cálculo de diversos tipos de curto-circuito em Sistemas Elétricos de Potência. Os
tipos de curto-circuito analisados são trifásico, fase-terra, fase-fase e fase-fase-terra.
Além dos valores de corrente de curto-circuito também são calculados os valores de
magnitude de tensão em todas as barras, correntes circulantes por todas as linhas
de transmissão, contribuições dos geradores síncronos e correntes de neutro. Este
projeto apresenta uma solução de baixo custo, rápida, fácil e confiável, visando a
larga utilização deste recurso por estudantes e engenheiros interessados no
assunto.
5
ABSTRACT
This work aims to develop a computer program for calculating various types of shortcircuit in power systems. The types of short-circuit analyzed are three-phase, phaseground, phase-phase and phase-phase-ground. In addition to the current values of
short circuit are also calculated the values of voltage magnitude at all buses,
circulating currents for all the transmission lines, the contributions of synchronous
generators and neutral currents. This project features a low-cost solution, quick, easy
and reliable, aiming the wide use of this resource for students and engineers
interested in the subject.
6
LISTA DE FIGURAS
Figura 2.1: Diagrama Unifilar...................................................................................20
Figura 2.2: Diagrama de Reatância.........................................................................20
Figura 2.3: Modelo por fase da Linha de Trasmissão Curta.................................20
Figura 2.4: Modelo π da Linha de Transmissão Média.........................................21
Figura 2.5: Modelo T da Linha de Transmissão Média..........................................21
Figura 2.6: Circuito equivalente por fase de uma Linha de Transmissão..........22
Figura 2.7: Modelo por fase do Gerador Síncrono................................................22
Figura 2.8: Circuito equivalente por fase do Transformador...............................23
Figura 2.9: Modelo por fase do Transformador.....................................................23
Figura 3.10: Seqüência Positiva..............................................................................26
Figura 3.11: Seqüência Negativa.............................................................................26
Figura 3.12: Seqüência Zero....................................................................................27
Figura 3.13: Transformador Tipo Core....................................................................34
Figura 3.14: Transformador Tipo Shell...................................................................34
Figura 4.15: Curto-circuito trifásico no gerador....................................................38
Figura 4.16: Curto-circuito no gerador...................................................................39
Figura 4.17: Curto-circuito monofásico a terra no gerador..................................40
Figura 4.18: Circuito equivalente série do curto-circuito monofásico a terra no
gerador.......................................................................................................................41
Figura 4.19: Curto-circuito bifásico.........................................................................42
Figura 4.20: Circuito equivalente paralelo do curto-circuito bifásico.................43
Figura 4.21: Curto-circuito bifásico a terra.............................................................44
Figura 4.22: Circuito equivalente paralelo do curto-circuito bifásico a terra.....45
Figura 5.23: Circuito RL equivalente de um Gerador Síncrono...........................55
Figura 5.24: (a - esquerda) Componente de Corrente alternada. (b - direita)
Componente de Corrente Contínua........................................................................56
7
Figura 6.25: Tela MatLab..........................................................................................60
Figura 6.26: Diagrama Unifilar utilizado como exemplo.......................................61
Figura 6.27: Curto-circuito trifásico na barra 1......................................................61
Figura 6.28: Curto-circuito trifásico na barra 2......................................................62
Figura 6.29: Curto-circuito trifásico na barra 3......................................................62
Figura 6.30: Curto-circuito fase-terra na barra 1...................................................64
Figura 6.31: Curto-circuito Bifásico na barra 1......................................................65
Figura 6.32: Curto-circuito Bifásico na barra 2......................................................66
Figura 6.33: Curto-circuito Bifásico na barra 3......................................................67
8
LISTA DE TABELAS
Tabela 2.1: Linha de Transmissão Curta................................................................21
Tabela 2.2: Linha de Transmissão Média...............................................................21
Tabela 3.3: Modelo de Gerador Síncrono para as três seqüências.....................30
Tabela 3.4: Modelo de Motor de Indução para as três seqüências......................32
Tabela 3.5: Modelo de Linha de Transmissão para as três seqüências.............33
Tabela 3.6: Modelo de Transformador tipo Shell e Core para a seqüência
Positiva e Negativa....................................................................................................35
Tabela 3.7: Modelo de Transformador tipo Shell para a seqüência zero............35
Tabela 3.8: Modelo de Transformador tipo Core para a seqüência zero............36
Tabela A.9: Dados de Linhas e Transformadores.................................................74
Tabela A.10: Reatância dos Geradores...................................................................80
9
LISTA DE SIGLAS
ANAFAS
CEPEL
LT
TC
PC
PU
ANSI
IEC 909
Hp
Rms
Rpm
Análise de Falhas Simultâneas
Centro de Pesquisas de Energia Elétrica
Linha de Transmissão
Transformador de Corrente
Personal Computer
Por Unidade
American National Standards Institute
International Electrotechnical Commission 909
Horse Power
Root Means Square
Rotações por minuto
10
SUMÁRIO
1 Introdução...............................................................................................................13
1.1 INTRODUÇÃO...................................................................................................13
1.2 ESTADO DA ARTE............................................................................................14
1.2.1 ANAFAS.....................................................................................................14
1.2.2 LAKU 15
1.2.3 CCTRI........................................................................................................15
1.3 OBJETIVOS.......................................................................................................15
1.4 ESTRUTURA DA MONOGRAFIA.....................................................................16
2 Representação do Sistema Elétrico de Potência...............................................17
2.1 INTRODUÇÃO...................................................................................................17
2.2 VALORES POR UNIDADE................................................................................17
2.3 VALORES BASES DAS GRANDEZAS ELÉTRICAS........................................17
2.4 DIAGRAMA UNIFILAR.......................................................................................19
2.5 LINHAS DE TRANSMISSÃO.............................................................................20
2.6 GERADOR SÍNCRONO....................................................................................22
2.7 TRANSFORMADOR..........................................................................................23
2.8 CARGAS............................................................................................................24
3 Componentes Simétricas......................................................................................25
3.1 INTRODUÇÃO...................................................................................................25
3.2 TEOREMA DE FORTESCUE............................................................................25
3.3 EXPRESSÃO ANALÍTICA DO TEOREMA DE FORTESCUE..........................27
3.4 ANÁLISE DE SEQÜÊNCIA ZERO.....................................................................28
3.5 REPRESENTAÇÃO DOS COMPONENTES DO SISTEMA ELÉTRICO NAS
SEQÜÊNCIAS POSITIVA, NEGATIVA E ZERO.....................................................29
3.5.1 Gerador Síncrono......................................................................................30
3.5.2 Linha de Transmissão...............................................................................32
11
3.5.3 Transformador...........................................................................................33
3.6 DESLOCAMENTO DE 30° EM UM TRANSFORMADOR Y-Δ .........................37
4 Cálculo de Curto-Circuito no Gerador Síncrono................................................38
4.1 INTRODUÇÃO...................................................................................................38
4.2 CURTO-CIRCUITO TRIFÁSICO.......................................................................38
4.3 CURTO-CIRCUITO MONOFÁSICO A TERRA.................................................40
4.4 CURTO-CIRCUITO BIFÁSICO..........................................................................42
4.5 CURTO-CIRCUITO BIFÁSICO A TERRA.........................................................43
4.6 MÉTODO DA MATRIZ PARA O CÁLCULO DE CURTO-CIRCUITO...............45
4.6.1 Cálculo da Matriz ......................................................................................46
4.7 CÁLCULO CURTO-CIRCUITO FASE TERRA - MÉTODO DA MATRIZ .........46
4.8 CÁLCULO CURTO-CIRCUITO FASE-FASE - MÉTODO DA MATRIZ ............49
4.9 CÁLCULO CURTO-CIRCUITO FASE-FASE-TERRA – MÉTODO DA MATRIZ
52
4.10 CÁLCULO CURTO-CIRCUITO TRIFÁSICO - MÉTODO DA MATRIZ ..........54
5 Variação da corrente de curto-circuito em função do tempo............................55
5.1 INTRODUÇÃO [9]..............................................................................................55
5.2 GRANDEZAS CARACTERÍSTICAS DO PROCESSO DE AMORTECIMENTO
56
5.2.1 Reatâncias do Gerador..............................................................................56
5.2.2 Constantes de tempo.................................................................................57
5.3 CÁLCULO DOS VALORES INSTANTÂNEOS DAS CORRENTES DE CURTOCIRCUITO................................................................................................................57
5.4 NORMAS ANSI E IEC 909 [7]-[8]......................................................................58
6 Resultados..............................................................................................................59
6.1 INTRODUÇÃO...................................................................................................59
6.2 ENTENDENDO O PROGRAMA........................................................................59
6.3 UTILIZANDO O PROGRAMA............................................................................59
12
6.4 RESULTADOS PARA SISTEMAS DE 3 BARRAS...........................................60
6.5 EXEMPLO 291 BARRAS...................................................................................69
7 Conclusões.............................................................................................................71
7.1 INTRODUÇÃO...................................................................................................71
7.2 APRENDIZADOS...............................................................................................71
7.3 TAREFAS REALIZADAS E OBJETIVOS ALCANÇADOS................................71
7.4 FUTUROS PROJETOS.....................................................................................71
13
1 INTRODUÇÃO
1.1
INTRODUÇÃO
Um curto-circuito ocorre quando há uma redução abrupta da impedância do
circuito entre dois pontos de potenciais diferentes gerando um aumento grande do
valor da corrente.
A simulação numérica de correntes de curto-circuito em pontos da rede
elétrica tem enorme importância no planejamento e coordenação da proteção, pois
permite prever as conseqüências dos mais diversos defeitos. Esse conhecimento
possibilita a tomada das medidas necessárias para minimizar essas conseqüências,
incluindo a instalação, ajuste e coordenação de dispositivos que promovem a
interrupção dos circuitos defeituosos, mas também garantem que todos os
componentes da rede são capazes de suportar os seus efeitos enquanto elas
persistirem.
Os curtos circuitos podem ser caracterizados de várias formas:
Duração: auto–extinguível, transitório e estacionário;
Origem: mecânica, sobretensões, falha de isolamento no interior ou exterior
de equipamentos;
Tipos: fase-terra (ɸ-terra, de maior incidência), fase-fase-terra (ɸ-ɸ-terra),
fase-fase (ɸ-ɸ) e trifásico (3ɸ, menor incidência, porém maior dano quanto à
estabilidade transitória).
O valor da corrente de curto-circuito é, praticamente, independente das
cargas da instalação, dependendo, na maior parte, da fonte e capacidade do
sistema. Os cálculos são utilizados para coordenação e dimensionamento da
proteção, evitando destruições e acidentes. Por isso, sempre quando houver
aumento da capacidade geradora ou mudança do sistema eles devem ser refeitos.
De forma geral, calculam-se as correntes de curto-circuito com os seguintes
objetivos:
Determinação do poder de interrupção de disjuntores e fusíveis, com a
previsão da corrente máxima de curto-circuito no ponto da rede onde estão
instalados;
14
Previsão dos esforços térmicos e eletrodinâmicos provocados pela passagem
da corrente, pois todos os elementos da rede, sobretudo barramentos e
seccionadoras, têm que suportar os efeitos destrutivos da passagem das
correntes de curto-circuito;
Coordenação das proteções, envolvendo a especificação das correntes e
tempos de disparo das mesmas.
Assim, o estudo do curto-circuito permite dimensionar as linhas de
transmissão (LTs) em relação ao seu limite térmico, definir a capacidade de
interrupção de disjuntores, dimensionar transformadores de corrente (TCs) quanto à
saturação, definir o ajuste de relés de proteção, analisar sobre e subtensões devido
ao curto-circuito, conhecer o tempo de atuação de relés e estudar a estabilidade
dinâmica do sistema elétrico.
1.2
ESTADO DA ARTE
Alguns dos programas existentes atualmente são citados a seguir.
1.2.1 ANAFAS
Criado pelo CEPEL (Centro de Pesquisas de Energia Elétrica), o ANAFAS
[1] (Análise de Falhas Simultâneas) é um programa computacional para cálculo de
curto-circuitos que permite a execução automática de grande número de faltas e
resultados orientados a pontos de falta ou de monitoração. Possui também serviços
auxiliares como cálculo de equivalentes e estudo de superação de equipamentos.
Cálculo de impedância equivalente de seqüência positiva entre barras. Permite
avaliar a proximidade elétrica entre duas barras quaisquer, considerando ou não a
presença dos geradores do sistema.
CEPEL-DRE pode fornecer gratuitamente versões acadêmicas de alguns de
seus programas para uso exclusivo em atividades educacionais em instituições de
ensino conforme as condições a seguir:
As versões acadêmicas apresentam uma série de limitações na dimensão
máxima dos sistemas que podem ser processados pelos programas. O limite
máximo é de 15 barras para a versão acadêmica do programa HarmZs e de
30 barras para as versões acadêmicas dos demais programas;
15
As versões acadêmicas dos programas não podem ser utilizadas para fins
não educacionais, mesmo por instituições de ensino. Para utilizar um
programa em projetos, estudos, serviços de consultoria ou em qualquer
atividade remunerada deve ser contratada a respectiva Licença de Uso.
1.2.2 LAKU
Criado pelo engenheiro Hans-Detlef Pannhorst, o LAKU [2] é um programa
para calcular fluxo de cargas e curto-circuitos de redes de transmissão de energia
elétrica. O programa desenvolvido para PCs pode rodar em Windows Vista,
Windows XP e Windows 2000 e ser usado em alemão e inglês.
A inserção de dados pode ser feita com melhores resultados utilizando o
editor gráfico NETDRAW (programa gráfico para estudos de redes de energia
elétricas). Os dois programas podem se comunicar entre si, isto é, LAKU pode ser
trazido diretamente do editor de gráficos depois de serem trocados os dados da
rede.
Este programa só pode ser usado para fins educacionais, não sendo
permitido o uso comercial. Não é permitida a modificação dos códigos e dados e não
é garantida a qualidade dos resultados obtidos. Este programa deve ser distribuído
sem nenhum custo.
1.2.3 CCTRI
O CCTRI [3] é um programa disponível em micros para cálculo de curtocircuito trifásico em sistemas elétricos industriais.
A limitação do programa ao cálculo de curto-circuito trifásico torna-o
defasado em relação à concorrência. O curto-circuito trifásico apesar de mais severo
é o de mais rara ocorrência. É de essencial importância o conhecimento das
correntes de um curto-circuito fase-terra, sendo o de mais freqüente ocorrência,
tornando-se imprescindível para o cálculo das proteções.
1.3
OBJETIVOS
16
Como visto anteriormente, existem no mercado programas para cálculo de
curto-circuito, porém ou são caros ou não confiáveis e difíceis de obter informações,
justificando o desenvolvimento deste programa: custo baixo, confiável e facilmente
acessível.
O objetivo deste projeto é desenvolver um programa computacional para
cálculo de diversos tipos de curto-circuito em Sistemas Elétricos de Potência. Os
tipos de curto-circuito analisados são trifásico, fase-terra, fase-fase e fase-fase-terra.
Além dos valores de corrente de curto-circuito também são calculados os valores de
magnitude de tensão em todas as barras, correntes circulantes por todas as linhas
de transmissão, contribuições dos geradores síncronos e correntes de neutro.
1.4
ESTRUTURA DA MONOGRAFIA
Esta monografia está dividida em 6 capítulos.
No primeiro apresentam-se objetivos do trabalho e programas existentes no
mercado.
No capítulo 2 e 3 descrevem-se o problema do cálculo de curto-circuito,
valores por unidade, diagrama unifilar, componentes simétricas, representação dos
componentes do sistema elétrico e análise e dedução das equações de cálculo de
curto-circuito.
O Capítulo 4 apresenta a formulação matemática para cálculo de curtocircuito, o Capítulo 5, resultados e, finalmente no Capítulo 6 as conclusões.
17
2 REPRESENTAÇÃO DO SISTEMA ELÉTRICO DE
POTÊNCIA
2.1
INTRODUÇÃO
Este capítulo apresenta a representação do Sistema Elétrico de Potência
voltado ao estudo do curto-circuito e proteção, pois cada componente deve ser
representado sob a ótica do seu comportamento frente às correntes de curto. Como
principais componentes da representação do sistema estão às reatâncias indutivas,
e a representação nas seqüências positiva, negativa e zero
2.2
VALORES POR UNIDADE
O sistema pu consiste na definição de valores de base para as grandezas
seguida da substituição dos valores das variáveis e constantes (expressas no
Sistema Internacional de unidades) pelas suas relações com os valores de base prédefinidos. As quantidades em pu expressam valores relativos, isto é, relativas ao
valor base. A escolha do valor base é importante.
As vantagens de se utilizar os valores em pu são:
Simplifica a visualização da grandeza porque os valores em pu estão
relacionados a um percentual;
Quando os cálculos são feitos em pu não há necessidade de referir todas as
impedâncias a um mesmo nível de tensão;
Os fabricantes fornecem dados em pu;
Modifica todos os transformadores para uma relação de 1:1;
Necessita-se apenas do valor em pu da impedância do transformador, sem
referir a qualquer lado (enrolamento);
Valores em pu dos equipamentos variam em uma faixa estreita enquanto os
valores reais variam amplamente.
2.3
VALORES BASES DAS GRANDEZAS ELÉTRICAS
Todo ponto elétrico é caracterizado por sua tensão, corrente, potência e
impedância. Conhecendo apenas duas dessas grandezas as outras duas podem ser
18
calculadas. A normalização pu utiliza como referência, comumente, a potência e a
tensão.
A potência aparente total base (
) é arbitrada levando em conta a
grandeza do sistema e é a mesma para todo o circuito. A potência aparente base do
sistema trifásico é a soma das potências aparentes base de cada fase.
A tensão base (
) é arbitrada, porém, normalmente, escolhe-se a tensão
nominal. Lembrando sempre que essa tensão deve obedecer às relações de
transformação sendo utilizada a tensão de linha e não a de fase. São utilizadas as
tensões de linha, pois para cálculo de proteção utilizam-se componentes simétricas
que são equilibradas para haver uma análise por fase.
(2.1)
(2.2)
(3.3)
(2.4)
A existência da
multiplicando a
se deve ao fato do sistema ser
trifásico e a tensão utilizada ser a de linha.
(2.5)
(2.6)
(2.7)
Os dados das características das máquinas (transformadores, geradores)
são fornecidos, normalmente, em pu, referidos aos valores nominais de potência e
tensão da máquina.
A compatibilização desses valores com as bases definidas requer uma
mudança de base: primeiramente isola-se a impedância em ohms na equação 2.6. A
19
impedância em ohms na base antiga é equivalente a impedância na base nova.
Utilizando a equação 2.7 e isolando a impedância nova, tem-se:
(2.8)
Uma das vantagens do uso de grandezas em pu, como citada
anteriormente, é no caso de transformadores. Em transformadores, a impedância
em pu referida ao primário e ao secundário é igual, desde que a corrente de
excitação seja desprezada, as tensões base obedeçam à relação do transformador e
a potência base seja comum às duas impedâncias. Prova-se essa equivalência
utilizando as equações 2.6, 2.7 e as relações de transformação do transformador:
(2.9)
(2.10)
A impedância em pu para as três fases ou para uma fase só em bancos de
transformadores trifásicos é igual: para o caso Y – Y o
da tensão de linha irá
anular o 3 que multiplica a potência monofásica, para o caso Δ – Δ o 3 da
impedância em Y irá anular o 3 que multiplica a potência monofásica e para o caso
Y – Δ a análise é feita em um dos lados utilizando os cálculos Y – Y ou Δ – Δ.
(2.11)
2.4
DIAGRAMA UNIFILAR
O diagrama unifilar representa uma fase do sistema trifásico equilibrado em
Y equivalente.
Já o diagrama de reatância representa os circuitos equivalentes
desses mesmos elementos, porém com suas reatâncias conectadas em cascata.
Ambos permitem uma visualização clara e concisa do circuito.
No sistema trifásico equilibrado a soma das correntes é equivalente a zero.
20
(2.12)
Os elementos do sistema elétrico são representados por símbolos
(modelagem por fase). A seguir exemplo de diagrama unifilar e diagrama de
impedância:
FIGURA 2.1: DIAGRAMA UNIFILAR
FIGURA 2.2: DIAGRAMA DE REATÂNCIA
2.5
LINHAS DE TRANSMISSÃO
O modelo da linha de transmissão varia de acordo com seu comprimento.
o Linhas de Transmissão Curtas
Para linhas de transmissão curtas o modelo (Figura 2.3) consiste em uma
resistência em série com uma reatância, cuja impedância é igual a:
(2.13)
Onde:
RLT – Resistência da linha de transmissão;
XLT – Impedância da linha de transmissão.
FIGURA 2.3: MODELO POR FASE DA LINHA DE TRASMISSÃO CURTA
A Tabela 2.1 [4] apresenta os valores de comprimento da linha, que
depende do nível de tensão, para uma Linha de Transmissão Curta.
21
TABELA 2.1: LINHA DE TRANSMISSÃO CURTA
Tensão de Linha (VL)
VL < 150 kV
150 kV ≤ VL < 400 kV
VL ≥ 400 kV
Comprimento máximo (L)
80 km
40 km
20 km
o Linhas de Transmissão Médias
Linhas de transmissão médias possuem dois modelos, π e T. O modelo π
consiste em uma impedância série com capacitores shunt nas suas extremidades,
como apresentado na Figura 2.4.
FIGURA 2.4: MODELO Π DA LINHA DE TRANSMISSÃO MÉDIA
Onde:
– Susceptância capacitiva total da linha da linha de transmissão.
O modelo T está representado na Figura 2.5.
FIGURA 2.5: MODELO T DA LINHA DE TRANSMISSÃO MÉDIA
A caracterização de uma linha média encontra-se na Tabela 2.2 [4].
TABELA 2.2: LINHA DE TRANSMISSÃO MÉDIA
Tensão de Linha (VL)
VL < 150 kV
150 kV ≤ VL < 400 kV
VL ≥ 400 kV
Comprimento máximo (L)
80 km ≤ L ≤ 200 km
40 km ≤ L ≤ 200 km
20 km ≤ L ≤ 100 km
o Linhas de Transmissão Longas
Linhas de transmissão longas possuem uma representação mais complexa.
Por isso utilizam-se os modelos π e T das linhas médias com os valores de
modificados.
(2.14)
e
22
(2.15)
(2.16)
Onde:
– Comprimento da linha de transmissão;
– Constante de propagação;
– Admitância shunt por unidade de comprimento;
– Impedância série por unidade de comprimento.
O circuito equivalente por fase de uma linha de transmissão encontra-se na
Figura a seguir. No programa é utilizado o modelo π de linhas de transmissão
médias.
FIGURA 2.6: CIRCUITO EQUIVALENTE POR FASE DE UMA LINHA DE TRANSMISSÃO
2.6
GERADOR SÍNCRONO
O gerador síncrono converte energia mecânica em elétrica quando operado
como gerador e energia elétrica em mecânica quando operado como motor. A
origem do nome é devida à operação da máquina ser com velocidade de rotação
constante sincronizada com a freqüência da tensão elétrica alternada aplicada nos
seus terminais.
O modelo do gerador síncrono (Figura 2.7) consiste em uma fonte de tensão
em série com uma reatância subtransitória.
FIGURA 2.7: MODELO POR FASE DO GERADOR SÍNCRONO
Onde:
23
G – Fonte de tensão;
X’’d – Reatância subtransitória do eixo direito.
2.7
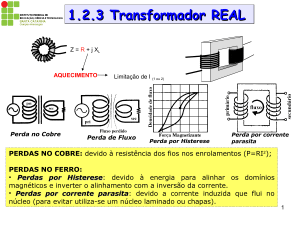
TRANSFORMADOR
O transformador transmite energia de um ponto a outro do circuito
transformando tensão, corrente ou impedância.
O circuito equivalente por fase do transformador pode ser simplificado da
Figura 2.8 para a Figura 2.9, pois como a corrente que flui para o curto-circuito é
alta, a corrente de excitação do núcleo é pequena podendo ser desprezada. O
modelo simplificado consiste em uma resistência em série com uma reatância.
FIGURA 2.8: CIRCUITO EQUIVALENTE POR FASE DO TRANSFORMADOR
Onde:
R1 – Resistência elétrica EQUIVALENTES do enrolamento primário;
X1 – Reatância equivalente do enrolamento primário, representando o fluxo disperso
na bobina;
R2 – Resistência elétrica do enrolamento secundário;
X2 – Reatância equivalente do enrolamento secundário, representando o fluxo
disperso na bobina;
Rf – Resistência elétrica equivalente que produz a mesma perda no núcleo que as
perdas por histerese e correntes parasitas;
Xm – Reatância equivalente de excitação, representando o fluxo resultante no
núcleo, necessário à operação normal do transformador.
FIGURA 2.9: MODELO POR FASE DO TRANSFORMADOR
24
(2.17)
(2.18)
Onde:
RT – Resistência equivalente do transformador;
XT – Reatância equivalente do transformador.
2.8
CARGAS
As cargas elétricas são consideradas no cálculo de curto-circuito
dependendo do tipo, tamanho, importância do sistema, e principalmente se o
sistema for isolado ou aterrado por meio de alta impedância.
25
3 COMPONENTES SIMÉTRICAS
3.1
INTRODUÇÃO
A utilização de componentes simétricas é necessária para a caracterização
do desbalanço da rede em sistemas polifásicos, ocasionado pelo curto-circuito.
Formulado por Fortescue, esse recurso é essencial no cálculo de curto-circuito para
sua simplificação, pois utiliza o cálculo monofásico.
O Teorema de Fortescue consiste na decomposição dos elementos de
tensão ou corrente das fases, em parcelas iguais, mas com ângulos de fase
diferentes. Desta forma é possível desmembrar o circuito polifásico em "n" circuitos
monofásicos, supondo válido o princípio da superposição, ou seja, que os circuitos
sejam lineares.
3.2
TEOREMA DE FORTESCUE
Fortescue por meio do teorema intitulado de “Método de componentes
simétricas aplicando a solução de circuitos polifásicos” estabeleceu que um sistema
de n fasores desequilibrados pode ser decomposto em n sistemas equilibrados,
denominado de componentes simétricas do sistema original.
Em componentes simétricas utiliza-se o operador imaginário ‘j’ e o rotacional
‘a’, que gira 120° um fasor.
(3.1)
(3.2)
Pelo foco ser sistemas trifásicos, as fases serão decompostas em três
sistemas
de
fasores
balanceados
(componentes
simétricas)
totalmente
desacoplados: seqüência positiva, negativa e zero.
A seqüência positiva ou direta (índice 1) é o conjunto de três fasores iguais
em módulo, girando no mesmo sentido e velocidade síncrona do sistema original,
defasados 120° entre si com a mesma seqüência de fases dos fasores originais.
Presentes durante condições trifásicas equilibradas.
26
FIGURA 3.10: SEQÜÊNCIA POSITIVA
(3.3)
(3.4)
(3.5)
A seqüência negativa ou indireta (índice 2) é o conjunto de três fasores
girando em uma direção contrária ao sistema original com as fases iguais em
módulo, defasadas 120° entre si com seqüência oposta à seqüência de fases dos
fasores originais. Medem a quantidade de desbalanço existente no sistema de
potência.
FIGURA 3.11: SEQÜÊNCIA NEGATIVA
(3.6)
(3.7)
(3.8)
A seqüência zero (índice 0) é o conjunto de três fasores gerados por um
campo magnético estático pulsatório com fases iguais em módulo, defasados 0°
27
entre si (em fase). Comumente associados ao fato de se envolver a terra em
condições de desbalanço.
FIGURA 3.12: SEQÜÊNCIA ZERO
(3.9)
3.3
EXPRESSÃO ANALÍTICA DO TEOREMA DE FORTESCUE
O sistema trifásico equilibrado resulta na superposição dos sistemas trifásicos
equilibrados descritos acima (seqüência positiva, negativa e zero). Sabe-se que:
(3.10)
Utilizando as equações anteriores chega-se na equação matricial:
(3.11)
Isolando as componentes simétricas da equação 3.11 teremos a equação
das componentes simétricas em função do sistema trifásico desbalanceado:
(3.12)
A mesma análise feita com a tensão pode ser realizada com a corrente.
Dessa análise pode-se retirar a expressão:
(3.13)
28
3.4
ANÁLISE DE SEQÜÊNCIA ZERO
Conclusões importantes são retiradas da análise da corrente e da tensão de
seqüência zero.
o CORRENTE
O estudo da corrente de seqüência zero tem grande importância, pois a partir
de sua interpretação são obtidas conclusões de aplicações físicas, diretamente
utilizadas na proteção de sistemas elétricos. Os próximos tópicos descrevem a
análise de cada caso da corrente de seqüência zero.
- Sistema Trifásico Estrela Aterrado
Aplicando a primeira lei de Kirchhoff no nó da estrela tem-se:
(3.14)
Substituindo-se a expressão 3.13 na equação 3.14 tem-se:
(3.15)
A partir deste resultado conclui-se que só é possível existir corrente de
seqüência zero em um Sistema de Neutro Aterrado.
- Sistema Trifásico Estrela
Aplicando a primeira lei de Kirchhoff no nó da estrela tem-se:
(3.16)
(3.17)
Em um Sistema Estrela Não Aterrado não há corrente de seqüência zero.
- Sistema Trifásico Delta (Triângulo)
Aplicando a primeira lei de Kirchhoff no delta (soma das correntes que entram
é igual à soma das que saem) tem-se:
29
(3.18)
(3.19)
Em um Sistema Delta também não há corrente de seqüência zero.
o TENSÃO
Os próximos tópicos descrevem a análise de cada caso da tensão de
seqüência zero.
- Sistema Trifásico Estrela
(3.20)
Como a expressão 3.20 não é necessariamente nula, há possibilidade de se
ter tensão de seqüência zero.
- Sistema Trifásico Delta (Triângulo)
Da equação 3.12, obtém-se a expressão:
(3.21)
Aplicando a lei das malhas no delta tem-se:
(3.22)
A partir das equações 3.21 e 3.22 conclui-se que, como o Sistema Delta não é
aterrado, não há possibilidade de se ter tensão de seqüência zero.
3.5
REPRESENTAÇÃO DOS COMPONENTES DO SISTEMA ELÉTRICO NAS
SEQÜÊNCIAS POSITIVA, NEGATIVA E ZERO
30
3.5.1 Gerador Síncrono
O gerador síncrono tenta fornecer às cargas uma tensão estável, garantindo
continuidade e estabilidade ao sistema. Na ocorrência do curto-circuito, ele injeta
correntes altas no sistema para compensar a queda de impedância, sendo, portanto,
o elemento ativo do curto.
Na seqüência positiva o gerador é um elemento ativo, gerando corrente. Na
seqüência negativa e zero ele é um elemento passivo. Para que haja fluxo de
corrente de seqüência zero é necessário um aterramento no neutro do gerador.
Para obterem-se as reatâncias de seqüência positiva, negativa e zero do
gerador síncrono é necessário analisar as correntes que passam pelo gerador
quando submetido a um curto-circuito trifásico.
As correntes de curto-circuito são assimétricas compostas por uma
componente contínua e uma alternada. Desconsiderando-se a componente
contínua, nota-se que a forma de onda de curto-circuito está contida em uma
envoltória decrescente que vai decaindo ciclo a ciclo até se estabilizar. Pode-se
caracterizar esta envoltória decrescente da corrente como uma reatância interna
variável subdividida no tempo: período subtransitório, transitório e regime
permanente. Como no período subtransitório a corrente de curto-circuito é a mais
elevada, utiliza-se esta reatância para modelar o gerador síncrono nas seqüências
positiva, negativa e zero.
(3.23)
A Tabela 3.1 apresenta o modelo do gerador síncrono para a seqüência
positiva, negativa e zero e para cada seqüência suas quatro possíveis ligações: Y, Y
aterrado, Y aterrado com impedância e delta.
TABELA 3.3: MODELO DE GERADOR SÍNCRONO PARA AS TRÊS SEQÜÊNCIAS
Seqüência Positiva
Seqüência Negativa
31
Seqüência Zero
Onde:
– Tensão de fase no terminal do gerador síncrono girando a vazio;
– Tensão da fase em relação ao neutro da seqüência positiva;
– Corrente de seqüência positiva da fase ‘a’ que sai dos enrolamentos da
máquina para o sistema;
– Reatância subtransitória do gerador por fase;
– Reatância de seqüência negativa por fase;
– Tensão de seqüência negativa da fase ‘a’ em relação ao neutro;
– Corrente de seqüência negativa que sai pela fase ‘a’ do gerador;
– Reatância de seqüência zero por fase;
– Tensão de seqüência zero da fase ‘a’ em relação ao neutro;
– Corrente de seqüência zero que sai pela fase ‘a’ do gerador;
– Impedância de aterramento.
Para motores síncronos, utilizam-se modelos equivalentes ao gerador
síncrono.
32
O motor de indução de grande porte se comporta como gerador elétrico
quando curto-circuitado. Se os dispositivos atuam com tempo maior que dois ciclos o
motor de indução pode ser desconsiderado.
A Tabela 3.2 apresenta o modelo do motor de indução para a seqüência
positiva, negativa e zero.
TABELA 3.4: MODELO DE MOTOR DE INDUÇÃO PARA AS TRÊS SEQÜÊNCIAS
Seqüência Positiva
Seqüência Negativa
Seqüência Zero
-
Onde:
– Tensão de fase no terminal do motor síncrono;
– Tensão de seqüência positiva;
– Corrente de seqüência positiva;
– Tensão de seqüência negativa;
– Corrente de seqüência negativa;
– Reatância de dispersão da bobina do estator;
– Reatância de dispersão da bobina do rotor referida ao estator.
3.5.2 Linha de Transmissão
A linha de transmissão é um elemento passivo que conecta todo o sistema
elétrico, por isso possui grande extensão e está exposta a todos os tipos de risco de
curto-circuito. Outra característica importante das LTs é o fato de possuírem alta
impedância, sendo um elemento limitador da corrente de curto-circuito.
A impedância de seqüência positiva da linha é a própria impedância normal da
LT.
33
O comportamento de uma linha de transmissão não se altera com as diferentes
seqüências de fase, por isso a impedância e o circuito equivalente de seqüência
negativa são os mesmos da seqüência positiva.
(3.24)
O circuito equivalente para seqüência zero, assim como o da seqüência
negativa, não se altera.
Mas, como os fasores da corrente de seqüência zero estão em fase, eles
induzem tensões no cabo de cobertura da linha de transmissão e no solo, originando
a circulação de corrente por esses elementos. Assim, a corrente de seqüência zero
pode retornar por qualquer caminho que não seja formado pelos próprios condutores
da linha. Desse modo, a impedância de seqüência zero depende do local do curtocircuito, da impedância equivalente da LT, cabo de cobertura e resistividade do solo.
A Tabela 3.3 apresenta o modelo de linha de transmissão para a seqüência
positiva, negativa e zero.
TABELA 3.5: MODELO DE LINHA DE TRANSMISSÃO PARA AS TRÊS SEQÜÊNCIAS
Seqüência Positiva
Seqüência Negativa
Seqüência Zero
Onde:
- Impedância de seqüência zero da LT;
- Impedância de seqüência positiva da LT que possui o mesmo valor da
impedância mostrada no item 2.5;
- Impedância de seqüência negativa da LT.
3.5.3 Transformador
O transformador é um elemento passivo no curto-circuito e se opõe à
passagem de corrente. Dependendo da seqüência (positiva, negativa ou zero) as
impedâncias das três seqüências se modificam.
34
A impedância de seqüência positiva e negativa são as mesmas. O
transformador é um elemento passivo, portanto qualquer seqüência de fase é vista
pelo transformador como positiva.
Porém, quanto à impedância de seqüência zero, deve-se observar que para
existir corrente de seqüência zero no primário deve existir caminho no secundário
para circulação da mesma.
Assim, a representação de transformadores na seqüência zero depende do
tipo de transformador, da ligação e da quantidade de enrolamentos.
Os transformadores são classificados quanto a: tipo (Shell ou núcleo envolvente
e Core ou núcleo envolvido); número de enrolamentos (2 eu 3 enrolamentos) e
ligação (estrela aterrado – estrela aterrado, delta – delta, estrela – estrela, estrela
aterrado – delta, delta estrela, estrela aterrado – estrela etc.).
O transformador do tipo Core é mais barato e fácil de fabricar, porém menos
eficiente. A Figura 3.4 apresenta um esquema monofásico deste tipo de
transformador.
FIGURA 3.13: TRANSFORMADOR TIPO CORE
O transformador do tipo Shell é mais eficiente, porém mais caro pois
necessita de mais tecnologia para sua construção. A Figura 3.5 apresenta um
esquema monofásico deste tipo de transformador.
FIGURA 3.14: TRANSFORMADOR TIPO SHELL
35
A Tabela 3.4 apresenta o modelo do transformador tipo Shell e Core para a
seqüência positiva e negativa.
TABELA 3.6: MODELO DE TRANSFORMADOR TIPO SHELL E CORE PARA A SEQÜÊNCIA
POSITIVA E NEGATIVA
Enrolamento
Conexão
2 enrolamentos
Todas
3 enrolamentos
Todas
Circuito equivalente
A Tabela 3.5 apresenta o modelo do transformador tipo Shell para a
seqüência zero.
TABELA 3.7: MODELO DE TRANSFORMADOR TIPO SHELL PARA A SEQÜÊNCIA ZERO
Conexão
Autotransformador
Circuito Equivalente
36
A Tabela 3.6 apresenta o modelo do transformador tipo Core para a
seqüência zero.
TABELA 3.8: MODELO DE TRANSFORMADOR TIPO CORE PARA A SEQÜÊNCIA ZERO
Conexão
Circuito Equivalente
37
Onde:
- Resistência do transformador;
- Reatância do transformador;
- Impedância do transformador com três enrolamentos do circuito primário;
- Impedância do transformador com três enrolamentos do circuito secundário;
- Impedância do transformador com três enrolamentos do circuito terciário;
- Reatância de seqüência zero;
- Reatância de seqüência positiva.
3.6
DESLOCAMENTO DE 30° EM UM TRANSFORMADOR Y-Δ
No caso de um transformador possuir a conexão Y-Δ (estrela - delta), as
correntes de linha na conexão estrela e na conexão delta ficam defasadas em trinta
graus uma em relação à outra.
Esse defasamento pode ser de mais ou menos trinta graus e depende de
como a bobina do lado delta está conectada. Sendo a seqüência de fase “abc”, para
o caso do começo da bobina da fase “a” do delta estar ligada no fim da bobina da
fase “b”, o deslocamento será de +30° na seqüência positiva e -30° na negativa.
38
4 CÁLCULO DE CURTO-CIRCUITO NO GERADOR
SÍNCRONO
4.1
INTRODUÇÃO
A análise e dedução das equações do cálculo de curto-circuito serão realizadas
para o modelo de um gerador síncrono, pois todas as conclusões obtidas a partir
desses cálculos podem ser estendidas a todo circuito elétrico através do Teorema
de Thevènin, cujo equivalente é análogo ao do gerador síncrono.
Os tipos de curtos-circuitos a serem implementados e analisados são o trifásico,
fase-terra, fase-fase-terra e fase-fase.
A ocorrência de curtos-circuitos é mais comum nas linhas de transmissão e
distribuição do sistema elétrico (em média 89% dos casos).
A falta trifásica é causadora de maiores danos ao sistema elétrico principalmente
quanto à estabilidade transitória, porém de ocorrência rara, em torno de 6% das
vezes.
Já a falta fase-terra é a mais corriqueira, pos ocorre em torno de 63% das
ocorrências. Pode ser causada por envelhecimento de isoladores, vento, queda de
arvores ou galhos, descargas atmosféricas, queimadas etc.
4.2
CURTO-CIRCUITO TRIFÁSICO
O curto-circuito trifásico possui apenas as componentes de seqüência positiva,
pois é equilibrado (as três fases são levadas a terra como na Figura 4.1).
FIGURA 4.15: CURTO-CIRCUITO TRIFÁSICO NO GERADOR
39
As condições do curto-circuito trifásico nos terminais do gerador síncrono a
vazio são:
(4.1)
Onde:
- Fasor tensão na fase a;
- Fasor tensão na fase b;
- Fasor tensão na fase c.
Substituindo os valores da expressão 4.1 na 3.12, obtém-se:
(4.2)
(4.3)
Portanto o circuito equivalente da seqüência positiva apresentado na Figura
4.1 está apresentado na Figura 4.2.
FIGURA 4.16: CURTO-CIRCUITO NO GERADOR
Conclui-se que:
E
I A1 =
jx1
(4.4)
Como o curto-circuito trifásico é equilibrado, as correntes de seqüência zero e
negativa são iguais a zero.
Utilizando-se da equação 3.12 referente à corrente e substituindo os valores
das correntes (4.4.) têm-se a equação para calcular as correntes nas fases A, B e C.
40
(4.5)
4.3
CURTO-CIRCUITO MONOFÁSICO A TERRA
A Figura 4.3 mostra o esquema de um curto-circuito monofásico no gerador
síncrono:
FIGURA 4.17: CURTO-CIRCUITO MONOFÁSICO A TERRA NO GERADOR
As condições de contorno para o curto-circuito fase-terra na fase A são:
(4.6)
(4.7)
Substituindo as condições do curto-circuito fase-terra na equação 3.12
referente à corrente:
(4.8)
(4.9)
41
Para representar essa igualdade das correntes de seqüências colocam-se os
circuitos equivalentes das seqüencia positiva, negativa e zero em série, como
mostra a Figura 4.4.
FIGURA 4.18: CIRCUITO EQUIVALENTE SÉRIE DO CURTO-CIRCUITO MONOFÁSICO A TERRA
NO GERADOR
Através da análise do circuito da Figura 4.4., conclui-se que:
(4.10)
Isolando
obtém-se:
(4.11)
A corrente de falta na fase A é obtida pela equação 3.11:
I A = 3 ⋅ I A1
(4.12)
As tensões de seqüência são calculadas por:
(4.13)
(4.14)
(4.15)
(4.16)
Com base nas equações acima é possível calcular as tensões nas fases A, B
e C do gerador síncrono através da expressão:
42
(4.17)
4.4
CURTO-CIRCUITO BIFÁSICO
Curto-circuito bifásico ocorre quando duas fases entram em curto-circuito
como, por exemplo, as fases B e C (Figura 4.5). Como o curto-circuito bifásico não
possui ligação a terra, não há como a corrente de seqüência zero circular, portanto
não possui a seqüência zero.
FIGURA 4.19: CURTO-CIRCUITO BIFÁSICO
O curto-circuito bifásico possui as seguintes condições de contorno:
(4.18)
(4.19)
(4.20)
Substituindo as condições do curto-circuito bifásico na equação 3.12:
(4.21)
43
Resolvendo a matriz obtém se:
(4.22)
(4.23)
Usando a equação 3.12 e resolvendo a equação matricial obtém-se:
(4.24)
(4.25)
Analisando a equação 4.25, pode-se concluir que no caso do curto-circuito
bifásico, os circuitos equivalentes das seqüências positiva e negativa podem ser
ligados em paralelo (Figura 4.6).
FIGURA 4.20: CIRCUITO EQUIVALENTE PARALELO DO CURTO-CIRCUITO BIFÁSICO
As correntes nas fases A, B e C do gerador síncrono são obtidas através de:
(4.26)
Resolvendo-se (4.26), as correntes nas fases B e C são:
(4.27)
4.5
CURTO-CIRCUITO BIFÁSICO A TERRA
44
Curto-circuito bifásico a terra ocorre quando duas fases entram em curtocircuito juntamente com a terra como, por exemplo, as fases B e C mostrado na
Figura 4.7.
FIGURA 4.21: CURTO-CIRCUITO BIFÁSICO A TERRA
As características deste defeito são:
(4.28)
(4.29)
Substituindo as condições do curto-circuito bifásico:
(4.30)
Resolvendo a matriz obtém-se:
(4.31)
Aplicando-se o Teorema de Fortescue junto às características desse curtocircuito têm-se:
(4.32)
45
Analisando as equações 4.31 e 4.32 pode-se concluir que no caso do curtocircuito bifásico-terra os circuitos equivalentes das seqüências positiva, negativa e
zero podem ser representados como se estivessem em paralelo (Figura 4.8).
FIGURA 4.22: CIRCUITO EQUIVALENTE PARALELO DO CURTO-CIRCUITO BIFÁSICO A TERRA
Através da análise do circuito da Figura 4.8 podem-se calcular as correntes
através do método do divisor de corrente. Aplicando-se os valores obtidos em 4.33 é
possível calcular as correntes nas fases A, B, C do gerador.
(4.33)
4.6
MÉTODO DA MATRIZ Z PARA O CÁLCULO DE CURTO-CIRCUITO
Uma opção para a investigação do curto-circuito elétrico em grandes sistemas é
usar métodos matriciais que, antigamente, eram inviáveis em virtude da falta de
recursos computacionais realmente eficientes. O método matricial para o cálculo de
curto-circuito é baseado na montagem da matriz de impedâncias de um sistema
elétrico, chamada Z barra .
A matriz Z barra contém as impedâncias no ponto de cada nó com relação a um
nó de referência escolhido arbitrariamente. A impedância no ponto de um nó é a
impedância equivalente entre ele e a referência. A matriz Z barra contém também a
impedância de transferência entre cada barra do sistema e cada outra barra, com
relação ao nó de referência. A matriz Z barra
pode ser calculada invertendo-se a
matriz que contém todas as admitâncias do sistema elétrico, a matriz Ybarra .
46
4.6.1 Cálculo da Matriz Ybarra
A equação de um sistema de n barras pode ser representada na forma
matricial abaixo.
(4.34)
ou
(4.35)
Onde:
I barra
- Vetor das correntes injetadas (a corrente é considerada positiva quando está
entrando em uma barra do sistema elétrico e negativa quando está saindo);
Vbarra
-
Vetor das tensões nas barras do sistema, tensões nodais medidas em
relação ao nó de referência;
Ybarra
- Matriz das admitâncias do sistema (os elementos da diagonal principal
correspondem à soma de todas as admitâncias conectadas àquela respectiva barra
ou nó. Já os elementos fora da diagonal principal correspondem ao negativo da
soma das admitâncias conectadas entre as barras ou nós).
A matriz admitância ( Ybarra ) pode ser montada através de uma simples
inspeção do sistema elétrico. Invertendo essa matriz obtém-se a matriz Z barra
necessária para o cálculo de curto-circuito utilizando o método da matriz Z .
4.7
CÁLCULO CURTO-CIRCUITO FASE TERRA - MÉTODO DA MATRIZ Z
Para o desenvolvimento das equações será suposto que o curto-circuito fase-
terra ocorreu na fase A, como mostrado anteriormente na Figura 4.3.
Primeiramente, é necessária a determinação das matrizes admitâncias de
barra para as seqüências positiva, negativa e zero (respectivamente Y 1, Y 2, Y 0).
47
Então através da inversão dessas matrizes, obtém-se as matrizes impedâncias para
cada uma das seqüências, positiva, negativa e zero ( Z 1, Z 2, Z 0).
A partir desses dados as correntes de seqüência e as correntes totais nas
fases que aparecem no sistema elétrico durante o curto-circuito fase-terra são
calculadas através das equações:
(4.36)
(4.37)
(4.38)
Onde:
- Corrente de falta de seqüência positiva na barra k, na fase A;
- Corrente de falta de seqüência negativa na barra k, na fase A;
- Corrente de falta de seqüência zero na barra k, na fase A;
- Corrente de falta total na barra k na fase A;
- Fasor tensão na barra k antes da ocorrência da falta;
- Elemento k-k da matriz Z .
As tensões de seqüência e totais que aparecem no sistema elétrico durante o
curto-circuito fase-terra são calculadas através das equações:
(4.39)
(4.40)
(4.41)
48
(4.42)
(4.43)
Onde:
- Tensão na fase A de seqüência positiva na barra k (durante a ocorrência da
falta na barra k);
- Tensão na fase A de seqüência negativa na barra k (durante a ocorrência da
falta na barra k);
- Tensão na fase A de seqüência zero na barra k (durante a ocorrência da falta
na barra k).
Assumindo que todas as tensões pré-falta são iguais à tensão pré-falta na
barra de falta k:
(4.44)
(4.45)
(4.46)
(4.47)
Onde:
- Tensão na fase A de seqüência positiva na barra genérica n (durante a
ocorrência da falta na barra k);
49
- Tensão na fase A de seqüência negativa na barra genérica n (durante a
ocorrência da falta na barra k);
- Tensão na fase A de seqüência zero na barra genérica n (durante a ocorrência
da falta na barra k);
- Tensão na fase A total na barra genérica n (durante a ocorrência da falta na
barra k).
Considerando que a impedância do elemento série entre duas barras i-m é:
(4.48)
A corrente
na fase A que percorre o elemento entre as barras i e m na
direção i-m é formada por uma reatância série (despreza-se a componente shunt), e
pode ser calculada a partir das tensões terminais
e
e dos parâmetros
equivalentes do modelo de linha curta.
(4.49)
(4.50)
(4.51)
(4.52)
Onde:
- Corrente total na fase A que percorre o elemento entre as barras i e m na
direção i-m.
4.8
CÁLCULO CURTO-CIRCUITO FASE-FASE - MÉTODO DA MATRIZ Z
Para o desenvolvimento das equações será suposto que o curto-circuito fase-
fase ocorra nas fases B e C, como mostrado anteriormente na Figura 4.5.
50
Os primeiros passos são os mesmos daqueles utilizados para curto-circuito
fase-terra. Primeiramente determinam-se as matrizes admitâncias ( Y 1, Y 2) e suas
inversas, as matrizes impedâncias ( Z 1, Z 2).
A partir desses dados as correntes de seqüência e as correntes totais nas
fases que aparecem no sistema elétrico durante o curto-circuito são dadas pela
equação:
(4.53)
Onde:
- Corrente de falta de seqüência positiva na barra k, na fase A;
- Corrente de falta de seqüência negativa na barra k, na fase A;
- Corrente de falta total na barra k na fase A;
- Tensão na barra k antes da ocorrência da falta;
- Elemento k-k da matriz Z .
As tensões de seqüência e totais que aparecem no sistema elétrico durante o
curto-circuito são dadas pelas equações:
(4.54)
Ou
(4.55)
(4.56)
(4.57)
(4.58)
51
(4.59)
Onde:
- Tensão na fase A de seqüência positiva na barra k (durante a ocorrência da
falta na barra k);
- Tensão na fase A de seqüência negativa na barra k (durante a ocorrência da
falta na barra k).
Assumindo que todas as tensões pré-falta são iguais à tensão pré-falta na
barra de falta k:
(4.60)
(4.61)
(4.62)
(4.63)
Onde:
- Tensão na fase A de seqüência positiva na barra genérica n (durante a
ocorrência da falta na barra k);
- Tensão na fase A de seqüência negativa na barra genérica n (durante a
ocorrência da falta na barra k);
- Tensão na fase A total na barra genérica n (durante a ocorrência da falta na
barra k).
Considera-se que a impedância do elemento série entre duas barras i-m é
representada pela equação 4.48.
A corrente
na fase A que percorre o elemento entre as barras i e m na
direção i-m é formada por uma reatância série (despreza-se a componente shunt), e
52
pode ser calculada a partir das tensões terminais
e
e dos parâmetros
equivalentes do modelo de linha curta, considerando apenas as equações 4.49 e
4.50, sendo a corrente da seqüência zero nula e a corrente total calculada pela
equação:
(4.64)
4.9
CÁLCULO CURTO-CIRCUITO FASE-FASE-TERRA – MÉTODO DA MATRIZ
Z
Para o desenvolvimento das equações será suposto que o curto-circuito fasefase-terra ocorra nas fases B e C, como mostrado anteriormente na Figura 4.7.
Os primeiros passos são os mesmos daqueles utilizados para curto-circuito
fase-fase, porém neste será incluso a seqüência zero devido à falta atingir a terra
também. Primeiramente determinam-se as matrizes admitâncias ( Y 1, Y 2, Y
0
)e
suas inversas, as matrizes impedâncias ( Z 1, Z 2, Z 0).
A partir desses dados as correntes de seqüência e as correntes totais nas
fases que aparecem no sistema elétrico durante o curto-circuito são dadas pelas
equações:
(4.65)
(4.66)
(4.67)
(4.68)
(4.69)
53
(4.70)
Onde:
- Corrente na hora da falta que passa pelo neutro e vai a terra.
As tensões de seqüência e totais que aparecem no sistema elétrico durante o
curto-circuito são dadas pelas equações:
(4.71)
(4.72)
(4.73)
Aplicando os resultados das tensões das seqüências positiva, negativa e zero
na equação 4.42 tem-se:
(4.74)
(4.75)
Assumindo novamente que todas as tensões pré-falta são iguais a tensão
pré-falta na barra de falta k:
(4.76)
(4.77)
(4.78)
E a corrente
na fase A que percorre o elemento entre as barras i e m
na direção i-m será calculada pelas mesmas equações existentes no curto-circuito
fase-terra, as expressões 4.49, 4.50, 4.51 e 4.53.
54
4.10 CÁLCULO CURTO-CIRCUITO TRIFÁSICO - MÉTODO DA MATRIZ Z
O cálculo do curto-circuito trifásico é o mais simplificado, pois este é um curtocircuito equilibrado, só existindo a seqüência positiva para ser analisada. Então é
necessário determinar a matriz admitância e impedância apenas da seqüência
positiva ( Y 1 e Z 1).
As correntes e as tensões para esse curto-circuito são calculadas facilmente
com base nas equações a seguir:
(4.79)
(4.80)
E a corrente
na fase A que percorre o elemento entre as barras i e m na
direção i-m será calculada pela equação 4.49 apenas, pois o curto-circuito trifásico
compreende apenas a seqüência positiva de fase.
55
5 VARIAÇÃO DA CORRENTE DE CURTO-CIRCUITO
EM FUNÇÃO DO TEMPO
5.1
INTRODUÇÃO [9]
As expressões apresentadas nos capítulos anteriores para o cálculo das
correntes de curto-circuito fornecem os valores eficazes de corrente alternada, que
consideram as impedâncias dos geradores e da rede.
Das impedâncias que intervêm num curto-circuito, a do gerador ocupa uma
posição particular, porque durante um curto-circuito o campo de excitação é
enfraquecido num grau maior ou menor, devido a reação do induzido e a tensão nos
terminais do gerador sofre uma queda proporcional, como conseqüência da
elevação da impedância do gerador. Quando esta impedância se eleva, a corrente
de curto-circuito se reduz, num grau tanto maior quanto mais próximo do gerador
onde ocorre o curto-circuito.
A corrente inicialmente se eleva a um valor de pico, representado pelo impulso
de corrente de curto-circuito I´´ (corrente sub-transitória), o qual se reduz, primeiro
acentuadamente, depois lentamente, até atingir o valor I (corrente permanente de
curto-circuito).
Ainda, devido às características indutivas do gerador que podem ser
simplificadamente representadas através do circuito RL da Figura 5.1, pode-se ainda
deduzir o valor instantâneo da corrente i(t):
(5.1)
FIGURA 5.23: CIRCUITO RL EQUIVALENTE DE UM GERADOR SÍNCRONO
A representação de i(t) para diferentes instantes de chaveamento estão
mostradas na Figura 5.2.
56
FIGURA 5.24: (A - ESQUERDA) COMPONENTE DE CORRENTE ALTERNADA. (B - DIREITA)
COMPONENTE DE CORRENTE CONTÍNUA.
A Figura 5.2 (a) mostra a corrente em função do tempo num circuito RL para
α – Θ = 0, onde Θ = tan-1 (ωL/R). A tensão é igual a І Vm І sen (ωt + α) aplicada no
instante t = 0. A Figura (b), a corrente em função do tempo num circuito RL para α –
Θ = - 90o, onde Θ = tan-1 (wL/R). A tensão é igual a І Vm І sen (ωt + α ) aplicada no
instante t = 0.
A corrente de curto-circuito se compõe assim de duas componentes, a
componente de corrente alternada que varia simetricamente em relação ao eixo
horizontal de referências e a componente de corrente contínua, que vem
representada em um dos lados deste mesmo eixo (Figura 5.2 b).
5.2
GRANDEZAS CARACTERÍSTICAS DO PROCESSO DE AMORTECIMENTO
5.2.1 Reatâncias do Gerador
A variação da corrente de curto-circuito, analisada anteriormente, mostra que
para se determinar com exatidão os valores instantâneos correspondentes aos
diferentes instantes, é necessário conhecer três reatâncias diferentes do gerador:
Reatância subtransitória (x´´d) que compreende a reatância de dispersão dos
enrolamentos do estator e do rotor do gerador, estando incluídos na
dispersão do rotor as influências do enrolamento de amortecimento e da
partes maciças do rotor.O valor relativo das reatâncias subtransitórias é, nos
turbogeradores, na ordem de 12% e nas máquinas de pólos salientes de
18%;
Reatância transitória (x´d) que compreende a reatância de dispersão dos
enrolamentos do estator e da excitação do gerador. Geralmente, seu valor é
mais elevado do que a reatância subtransitória;
57
Reatância síncrona (xd) engloba a reatância total do enrolamento rotor do
gerador.
Todas as reatâncias pertencem ao conceito de reatância positiva.
5.2.2 Constantes de tempo
As reatâncias do gerador analisadas acima determinam junto com as
impedâncias de rede, no trecho compreendido entre o gerador e o ponto de curtocircuito, os valores iniciais e finais do processo de amortecimento. Para se
determinar os instantes de tempo em que esses valores ocorrem, há necessidade de
se definir as constantes de tempo:
Constante de tempo subtransitória Td’’: depende das propriedades do circuito
de corrente do rotor e do enrolamento de amortecimento;
Constante de tempo transitória Td’: depende das propriedades amortecedoras
do circuito de excitação;
Constante de tempo da componente de corrente contínua Tg’: depende das
propriedades do circuito de corrente do estator.
5.3
CÁLCULO DOS VALORES INSTANTÂNEOS DAS CORRENTES DE CURTOCIRCUITO
A variação da corrente de curto-circuito em função do tempo é definida pela
seguinte equação:
(5.2)
Onde:
I´´ - corrente subtransitória;
I´ - corrente transitória;
I - corrente regime permanente.
58
O valor da corrente i(t) representa o valor instantâneo da corrente de curtocircuito num instante t e com um ângulo de fase de corrente α, no instante inicial do
curto. O primeiro termo da fórmula acima corresponde à parcela subtransitória da
corrente de curto-circuito; o segundo, à parte transitória; o terceiro, à parte da
componente de corrente contínua.
5.4
NORMAS ANSI E IEC 909 [7]-[8]
A fim de se considerar essas diferentes parcelas de corrente de curto-circuito
existem normas específicas tais como a ANSI e IEC 909.
Ambas as normas provêm resultados conservativos para avaliar ou
determinar a capacidade do equipamento elétrico e requerem essencialmente os
mesmos dados para sistemas industriais típicos, porém a IEC 909 apresenta um
método mais apurado e complexo de ser calculado.
Diferenças são esperadas quando simulações numéricas são aplicadas para
os dois modelos. Essas diferenças foram analisadas e parecem ser diretamente
ligadas ao modelo de rede, modelo de rotação do equipamento e a procedimentos
computacionais.
Simulações computacionais realizadas com os dois procedimentos sugerem
que a adesão a qualquer procedimento tem de ser do início ao fim para resultados
consistentes. A utilização de dados de um procedimento em outro pode gerar erros
de simulação significativos.
As principais diferenças entre as normas são quanto ao modo de cálculo do
decaimento AC e DC das correntes de curto-circuito.
O decaimento AC está associado à tendência inerente das máquinas de
aumentar suas reatâncias com o tempo desde o início do curto-circuito. Já o
decaimento DC está estreitamente relacionado com o momento exato de interrupção
e as propriedades de amortecimento do circuito interrompido. A norma ANSI utiliza a
razão X/R.
Quanto maior o valor dessa razão maior é a assimetria e mais lento o
decaimento. Devido à alta relação X/R do enrolamento de um gerador, o fator de
assimetria é maior para faltas nas barras de geração ou em linhas de alto ângulo
próximos destas barras.
59
6 RESULTADOS
6.1
INTRODUÇÃO
O programa calcula facilmente diversos tipos de curto-circuito em Sistemas
Elétricos de Potência: trifásico, fase-terra, fase-fase e fase-fase-terra. Tem como
resposta valores, para curtos em todas as barras, de corrente de curto-circuito e de
magnitude de tensão em todas as barras.
6.2
ENTENDENDO O PROGRAMA
O programa contém sete arquivos:
Dados.m: contém os dados do sistema (número de barras, linhas, geradores
e transformadores; barra onde estão os geradores; localização das linhas e
transformadores; reatâncias positiva, negativa e zero das linhas, geradores e
transformadores; reatâncias transitória e síncrona de seqüência positiva do
gerador; capacitores shunt da linha; banco de capacitores; tap e tipo dos
transformadores);
Dados_adicionais.m: contém os dados para cálculo dos gráficos (barra e tipo
do curto; período transitório, subtransitório e contínuo).
MontaMatrizes_ZBarra.m: monta as matrizes de admitância Y1, Y2 e Y0 e a
matriz de impedância Z0 utilizando os conhecimentos do Capítulo 4;
CurtoCircuito.m: possui os cálculos das correntes e tensões de curto (também
utilizando os conhecimentos e fórmulas do Capítulo 4);
Grafico_corrente.m: calcula e gera o gráfico do decaimento exponencial da
corrente de curto-circuito (Plotar_Grafico.m);
Plotar_Grafico.m: gráfico do decaimento exponencial da corrente de curtocircuito;
Saída.out: arquivo de saída, gerado após a execução do arquivo
CurtoCircuito.m. Contém as correntes e tensões de curto-circuito em todas as
barras.
6.3
UTILIZANDO O PROGRAMA
60
Primeiramente é necessário ter instalado no computador o software MatLab.
Então siga os passos seguintes:
1 – Salve uma pasta no seu computador com os seguintes arquivos:
CurtoCircuito.m,
Dados.m,
Dados_adicionais.m,
Grafico_Corrente.m;
Plotar_Grafico.m e MontaMatrizes_ZBarra.m;
2 – Insira os dados do sistema a ser calculado o curto nos arquivos Dados.m e
Dados_adicionais (caso queira o gráfico do decaimento exponencial da corrente de
curto-circuito);
3 – Abra a pasta no MatLab (indicado na Figura 5.1);
4 – Digite “CurtoCircuito” após “>>” no MatLab (indicado na Figura 5.1);
5 – Tecle “Enter”;
6 – Digite “Grafico_corrente” após “>>” no MatLab;
7 Tecle “Enter”.
FIGURA 6.25: TELA MATLAB
O resultado aparecerá na tela do MatLab e um arquivo com os resultados
será criado (saida.out).
6.4
RESULTADOS PARA SISTEMAS DE 3 BARRAS
Será apresentado a seguir o cálculo de curto-circuito utilizando como exemplo
o sistema elétrico da Figura 6.2.
61
Figura 6.26: Diagrama Unifilar utilizado como exemplo
Considera-se:
Período transitório = 1.3 segundos
Período contínuo = 0.15 segundos
Reatâncias: Subtransitória = 0.15j
Transitória = 0.21j
Síncrona (permanente) = 1.2j
1.1.1 Cálculo de Curto-Circuito Trifásico
- Cálculo para curto na barra 1:
Figura 6.27: Curto-circuito trifásico na barra 1
Cálculo da corrente de curto-circuito:
Nas linhas 1 (linha de transmissão) e 2 (transformador) a corrente será
nula pois o curto-circuito ocorrido na barra 1 impede que corrente flua neste sentido.
62
Não há necessidade de calcularmos a tensão nas barras pois a falta na barra
1 ocasionará uma tensão nula neste ponto e nos próximos porque não serão
supridos pelo gerador.
Lembrando que as fases a, b e c em curtos trifásicos possuem mesmo
módulo e defasamento de 120 graus.
- Cálculo para curto na barra 2:
Figura 6.28: Curto-circuito trifásico na barra 2
A corrente na linha 2 nada mais é que a corrente de curto somada de 30
graus.
A corrente na linha 1 é nula pois um curto na barra 2 faz com que não flua
corrente nesse sentido.
A tensão na barra 1 é calculada através da reatância do gerador, corrente que
passa por ele e tensão do gerador.
A tensão nas barras 2 e 3 é nula.
- Cálculo da corrente para curto na barra 3:
Figura 6.29: Curto-circuito trifásico na barra 3
63
Corrente na linha 1 é a corrente de curto-circuito. A corrente na linha 2 é a
corrente da linha 1 subtraída em 30 graus por causa do transformador.
A tensão na barra 2 é a corrente na linha 1 multiplicada pela impedância da
linha.
A tensão na barra 1 é a tensão do gerador subtraída de sua queda de tensão.
A Figura 6.3 apresenta a evolução da envoltória da corrente de curto-circuito
trifásica simétrica e assimétrica quando o curto ocorre na barra 1.
FIGURA 6.3: CORRENTE PARA CURTO TRIFÁSICO NO GERADOR
1.1.2 Cálculo de Curto-Circuito Fase-Terra
- Cálculo para curto na barra 1:
64
Figura 6.30: Curto-circuito fase-terra na barra 1
Cálculo da corrente de curto-circuito:
Utilizando a equação 4.9:
Calculo das tensões na barra de curto (1):
- Cálculo para curto na barra 2:
Figura 6.7: Curto-circuito fase-terra na barra 2
Cálculo da corrente de curto-circuito:
Utilizando a equação 4.9:
Calculo das tensões na barra de curto (2):
65
Aplicando teorema de fortescue:
Calculo das tensões na barra 1:
Aplicando teorema de fortescue:
1.1.3 Cálculo de Curto-Circuito Fase-Fase
- Cálculo para curto na barra 1:
Figura 6.31: Curto-circuito Bifásico na barra 1
Cálculo da corrente de curto-circuito:
Aplicando a equação 3.11 aplicada à corrente obtém-se:
66
A tensão na barra de curto-circuito (barra 1):
Aplicando a equação 3.11 obtém-se:
Nas linhas 1 (linha de transmissão) e 2 (transformador) a corrente será nula
pois o curto-circuito ocorrido na barra 1 impede que corrente flua neste sentido.
Portanto a tensão nas outras barras é a mesma que a da barra 1 de curto circuito,
são apenas aplicadas ao lado estrela aterrado do transformador.
- Cálculo para curto na barra 2:
Figura 6.32: Curto-circuito Bifásico na barra 2
Cálculo da corrente de curto-circuito:
Aplicando a equação 3.11 aplicada à corrente obtém-se:
A tensão na barra de curto-circuito (barra 2):
67
Aplicando a equação 3.11 obtém-se:
Como a corrente na linha 1 (da barra 2 a 3) é nula a tensão na barra 3 será a
mesma da calculada para barra 2.
A tensão e corrente na barra 1 – lado estrela aterrado do transformador:
Devido ao transformador estrela aterrado delta entre as barras 1 e 2 a
corrente de seqüência positiva no lado estrela aterrado será -30° defasada e a
corrente de seqüência negativa será 30°defasada.
Aplicando a equação 3.11 para as correntes obtém-se:
Aplicando novamente a equação 3.11 obtém-se:
- Cálculo para curto na barra 3:
Figura 6.33: Curto-circuito Bifásico na barra 3
Cálculo da corrente de curto-circuito:
68
Aplicando a equação 3.11 aplicada à corrente obtém-se:
A tensão na barra de curto-circuito (barra 3):
Aplicando a equação 3.11 obtém-se:
Tensão na barra 2:
Aplicando novamente a equação 3.11 obtém-se:
A tensão e corrente na barra 1 – lado estrela aterrado do transformador:
Devido ao transformador estrela aterrado delta entre as barras 1 e 2 a
corrente de seqüência positiva no lado estrela aterrado será -30° defasada e a
corrente de seqüência negativa será 30°defasada.
Aplicando a equação 3.11 para as correntes obtém-se:
69
Aplicando novamente a equação 3.11 obtém-se:
6.5
EXEMPLO 291 BARRAS
Os dados do sistema de 291 barras, que é o equivalente do estado do Paraná,
encontram-se no Anexo A.
Considerando, por exemplo, um curto-circuito na barra do gerador 103, a
Tabela 6.13 apresenta os valores de correntes para os 4 tipos de curto-circuito, bem
como as tensões na barra em curto.
TABELA 6.13: CORRENTES E TENSÕES PARA CURTOS NA BARRA 103
Corrente (pu)
B
A
3Φ
Φ-terra
ΦΦ
ΦΦ-
20
22,3
0
0
-90
-90
0
0
20
0
17,3
21,5
-150
0
180
144
Tensão (pu) na Barra 103
A
B
c
C
20
0
17,3
21,5
30
0
0
36
0
0
1
0,87
0
0
0
0
0
0,95
0,5
0
0
-114
180
0
0
0,95
0,5
0
0
114
180
0
terra
A Figura 6.4 apresenta a evolução da envoltória da corrente de curto-circuito
trifásica simétrica e assimétrica quando o curto ocorre na barra 103.
70
FIGURA 6.4: CURTO-CIRCUITO TRIFÁSICO NO GERADOR DA BARRA 103
71
7 CONCLUSÕES
7.1
INTRODUÇÃO
Os objetivos foram alcançados fornecendo, desta maneira, ao mercado
interessado (estudantes, professores e profissionais da área de curto-circuito) um
programa de cálculo de curto-circuito gratuito e fácil de ser utilizado.
Os aprendizados foram inúmeros e a realização deste projeto gratificante.
7.2
APRENDIZADOS
Pôde-se ter a real conscientização da importância de todas as matérias
cursadas, dentre elas pode-se citar: Cálculo, Circuitos, Transformadores, Cálculo de
Curto-Circuito, etc. A construção do aprendizado durante os 5 anos de curso fez
com que ao final pudesse ser realizado esse trabalho.
A
matéria
“Projeto
de
Graduação”
uniu
todos
os
conhecimentos
anteriormente adquiridos e gerou a certeza do aprendizado fornecendo também a
capacidade de criação e gerenciamento de um projeto.
Os benefícios trazidos por esse projeto garantem que o engenheiro saia da
universidade pronto para o mercado, capaz de aplicar na prática a teoria vista em
sala de aula.
7.3
TAREFAS REALIZADAS E OBJETIVOS ALCANÇADOS
Seguindo o cronograma inicialmente criado, o projeto passou pelas etapas
necessárias para a elaboração de um programa de cálculo de curto-circuito
confiável.
O projeto escrito foi gerado para dar ao usuário do programa todo o
conhecimento necessário para o seu entendimento. A base de cálculo de curtocircuito é abordada completa e claramente. Além da ajuda ao usuário, também
ajudou as alunas a revisar o conteúdo e assim gerar corretamente o programa.
7.4
FUTUROS PROJETOS
72
Futuros projetos podem ser criados a partir deste. Uma idéia é aprofundar
na área de Sistemas Industriais, outra é tornar o sistema mais robusto. Espera-se
que haja continuidade ao estudo, pois essa a área de curto-circuito é
importantíssimo para qualquer sistema elétrico. As autoras estão a disposição para
possíveis dúvidas e ajudas na produção de um projeto no tema abordado.
73
REFERÊNCIAS
[1] http://www.anafas.cepel.br/ - Acessado em 03/08/2009
[2] http://www.netdraw.de/laku_pt.htm/ - Acessado em 14/09/2009
[3] http://cat.inist.fr/?aModele=afficheN&cpsidt=5032778/ - Acessado em 14/09/2009
[4] KINDERMANN, G.: “Curto-Circuito” – 4ª Edição, UFSC EEL LabPlan,
Florianópolis, 2007.
[5] Caderno e material da disciplina Cálculo de Curto-Circuito com professora
Thelma Fernandes – 2008.
[6] Modelagem de Transformadores Trifásicos de Distribuição para Estudos de
Fluxo de Potência –
Disponível em http://www.ufjf.br/ppee/files/2008/12/211035.pdf
[7] KNIGHT, G. e SIELING, H.; “Comparison of ANSI and IEC 909 Short-Circuit
Current Calculation Procedures”.
[8] RODOLAKIS, A.; “A Comparison of North American (ANSI) and European
(IEC) Fault Calculations Guidelines”.
[9] SIEMENS; “Correntes de curto-circuito em redes trifásicas”.
74
ANEXO A
Dados do Sistema de 291 barras
TABELA A.9: DADOS DE LINHAS E TRANSFORMADORES
De
126
7
6
14
15
77
8
7
11
9
9
12
14
87
12
37
37
26
26
30
30
108
108
68
68
28
29
27
29
30
30
31
29
26
29
33
34
118
271
38
27
118
42
27
42
39
39
43
124
36
Para
1
2
3
4
5
6
7
10
10
11
12
13
13
14
15
16
17
18
19
20
21
22
23
24
25
26
28
29
32
32
33
33
34
35
35
35
35
36
36
39
40
42
43
44
44
45
46
46
47
48
X
0,0001
0,02163
0,0327
0,0674
0,02825
0,0549
0,1078
0,0182
0,07237
0,0001
0,0361
0,0072
0,2343
0,1742
0,0248
0,0084
0,0336
0,06823
0,06823
0,0484
0,1936
0,0102
0,0408
0,014
0,042
0,0113
0,0126
0,0161
0,0164
0,0638
0,0756
0,011
0,0262
0,0039
0,0182
0,0338
0,0001
0,0647
0,0067
0,2162
0,1258
0,1807
0,1091
0,0807
0,0212
0,0725
0,1675
0,0238
0,11475
0,1651
Bshunt
0,01135
0
0
0
0
0,06009
0
1,022
0
0
0,1175
0,0236
0
0,0073
0,0807
0
0
0
0
0
0
0
0
0
0
0,02258
0,02432
0,03187
0,0316
0,11175
0,13268
0,02128
0,0454
0,00783
0,03624
0,06526
0
0
0
0,0534
0,24698
0,3015
0
0,14211
0,0382
0,01797
0,04146
0,00586
0,19687
0,04285
Tipo
Linha
Transformador
Transformador
Transformador
Transformador
Linha
Transformador
Linha
Transformador
Linha
Linha
Linha
Transformador
Linha
Linha
Transformador
Transformador
Transformador
Transformador
Transformador
Transformador
Transformador
Transformador
Transformador
Transformador
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Transformador
Transformador
Linha
Linha
Linha
Transformador
Linha
Linha
Linha
Linha
Linha
Linha
Linha
75
36
45
38
48
52
53
55
58
55
109
59
53
54
56
51
59
132
57
64
53
60
57
60
61
56
62
121
74
72
75
71
73
80
71
77
72
73
60
51
73
74
75
87
86
80
89
88
88
90
15
40
42
89
92
91
93
97
41
94
92
100
49
49
50
50
53
54
57
59
60
60
61
62
62
62
63
63
64
65
65
66
66
67
67
69
70
70
72
77
78
78
81
81
81
82
82
83
83
84
85
85
85
85
86
88
89
90
91
93
94
95
95
95
95
96
98
98
98
99
99
101
101
0,2261
0,2261
0,0595
0,11058
0,0664
0,1255
0,0911
0,0636
0,0664
0,0636
0,146
0,2019
0,0778
0,1531
0,0964
0,1214
0,08344
0,1113
0,2053
0,0509
0,193
0,1373
0,1424
0,095
0,0313
0,1586
0,0659
0,1373
0,0753
0,1369
0,1418
0,1876
0,0651
0,0607
0,1919
0,0177
0,1199
0,1848
0,2172
0,194
0,1382
0,1359
0,3867
0,0001
0,0568
0,0637
0,0484
0,1226
0,1521
0,1029
0,0809
0,1352
0,1135
0,0815
0,2148
0,1293
0,0588
0,1648
0,1181
0,1114
0,0671
0,06215
0,06215
0,01505
0,02822
0
0,03133
0,02401
0
0,01726
0
0,036
0,04732
0,0193
0,03589
0,0237
0,0299
0,14643
0,02742
0
0,01297
0,05083
0,03727
0,03518
0,0235
0,00926
0,04089
0
0,03727
0,02029
0,03713
0,033
0,04325
0
0,0141
0,0472
0,00435
0,0278
0
0,05383
0,0447
0,03739
0,0335
0
0
0,0979
0
0,01232
0,03103
0,03754
0,1782
0,1414
0,22765
0,1905
0,02099
0,05413
0,03254
0
0,04476
0,02915
0,02834
0
Linha
Linha
Linha
Linha
Transformador
Linha
Linha
Transformador
Linha
Transformador
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Transformador
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Transformador
Linha
Linha
Linha
Linha
Linha
Transformador
Linha
Linha
Linha
Linha
Transformador
Linha
Linha
Linha
Linha
Transformador
Linha
Linha
Transformador
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Transformador
Linha
Linha
Linha
Transformador
76
98
101
102
102
98
101
27
117
123
232
107
52
81
132
132
132
132
134
134
37
68
118
47
122
47
89
117
117
119
124
34
35
58
117
124
126
129
89
97
130
9
100
11
80
121
52
109
118
121
132
68
108
126
229
64
132
125
59
156
163
31
103
103
103
104
105
105
106
106
106
107
108
109
110
111
112
113
114
115
116
117
117
117
118
119
120
121
122
123
123
123
124
124
125
126
127
128
128
129
129
129
130
130
131
131
131
132
132
132
132
133
134
134
134
135
136
136
137
138
139
141
142
0,0215
0,0404
0,0061
0,0001
0,0368
0,0267
0,01146
0,0255
0,0044
0,0127
0,0073
0,0699
0,0127
0,0227
0,06809
0,03391
0,06782
0,01136
0,04545
0,00124
0,00654
0,01207
0,12652
0,02922
0,04708
0,11229
0,02048
0,0269
0,01603
0,01163
0,0001
0,0001
0,0001
0,02012
0,09776
0,01394
0,01272
0,03361
0,0182
0,02503
0,0822
0,0001
0,19343
0,0001
0,07836
0,0769
0,0089
0,15738
0,17777
0,47874
0,00697
0,01171
0,0194
0,4221
0,07732
0,15885
0,19006
0,0436
0,435
0,1666
0,0168
0,00543
0,0113
0,0016
0
0,01123
0,00844
0
3,1272
0,4758
0
0,7806
0,12617
0,00485
0
0
0
0
0
0
0,15204
0,80493
0
0,21706
3,604
0,08077
0,19327
2,5017
3,364
1,9589
0
0,00033
0,00033
0
2,4577
0,16845
1,7028
0
0,1056
0,03725
0,0777
0,2675
0
0,03904
0
0,13486
0,1381
0,01632
0,27123
0,30603
0
0,85746
1,2458
2,3697
0,0076
0,13568
0,27375
0,44274
0,01095
0
0
0,03236
Linha
Linha
Linha
Linha
Linha
Linha
Transformador
Linha
Linha
Transformador
Linha
Linha
Linha
Transformador
Transformador
Transformador
Transformador
Transformador
Transformador
Linha
Linha
Transformador
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Transformador
Linha
Linha
Linha
Linha
Linha
Linha
Transformador
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Transformador
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Transformador
Transformador
Linha
77
35
140
142
27
29
147
148
149
152
28
147
151
151
30
273
156
148
163
32
148
152
169
162
161
32
145
146
155
170
167
168
172
148
153
145
152
174
144
152
158
147
149
161
163
34
145
33
150
154
169
176
182
186
188
34
144
160
176
190
144
147
142
143
143
148
152
152
153
154
155
157
157
157
159
162
162
163
164
165
166
167
170
171
172
174
175
175
175
175
175
177
178
178
179
179
180
181
182
183
184
184
185
185
185
185
187
188
189
189
189
189
189
189
189
189
190
190
190
190
191
192
192
0,0188
0,0303
0,104
0,065
0,1803
0,0626
0,0116
0,0274
0,1228
0,1785
0,0564
0,0099
0,0399
0,0649
0,0056
0,1343
0,0245
0,2203
0,0205
0,1076
0,1111
0,4242
0,1497
0,0277
0,1884
0,0877
0,0497
0,0667
0,0641
0,1421
0,1292
0,0719
0,0191
0,013
0,119
0,3564
0,014
0,026
0,2872
0,1565
0,0389
0,0317
0,0292
0,5494
0,0142
0,059
0,1911
0,0569
0,0698
0,0551
0,1113
0,0302
0,107
0,0551
0,1886
0,0794
0,0535
0,0699
0,0837
0,0404
0,0821
0,0363
0,0077
0
0
0
0,00095
0,0033
0,00069
0,00236
0
0,00086
0,00016
0,00066
0
0
0,00204
0,00699
0,0036
0,03729
0,02859
0,00213
0,008
0,04074
0,00066
0
0,00134
0,00103
0,00142
0,00143
0,03497
0,03567
0,01969
0,00546
0,00378
0,00232
0,00596
0,00039
0,00046
0,00444
0,00248
0,00062
0,00078
0,00066
0,00854
0,0284
0,00101
0
0,00096
0,0013
0,00089
0,0019
0,00085
0,0017
0,00094
0
0,00155
0,00081
0,00112
0,00134
0,00071
0,00151
Linha
Linha
Transformador
Transformador
Transformador
Linha
Linha
Linha
Linha
Transformador
Linha
Linha
Linha
Transformador
Transformador
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Transformador
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Transformador
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Transformador
Linha
Linha
Linha
Linha
Linha
Linha
78
145
35
151
160
190
173
189
193
146
154
186
162
168
157
191
150
190
145
158
172
43
38
147
152
40
206
47
208
210
214
212
208
216
43
204
208
65
205
222
223
66
84
66
69
36
133
226
225
53
66
52
125
144
194
51
53
244
85
72
233
78
193
194
194
194
194
195
195
195
196
196
197
198
198
199
199
200
200
201
201
202
203
205
207
207
208
208
209
211
215
215
216
217
217
219
219
220
221
222
224
224
225
226
227
227
228
229
229
230
231
231
232
232
235
235
236
236
237
238
240
241
242
0,059
0,1836
0,0936
0,0531
0,001
0,028
0,0492
0,0059
0,0325
0,0213
0,0639
0,2318
0,029
0,0083
0,0119
0,1111
0,0541
0,0461
0,1145
0,0083
0,0331
0,3597
0,0423
0,0167
0,0639
0,0513
0,0004
0,0028
0,0389
0,5032
0,3274
0,848
0,454
0,0354
0,0175
0,0175
0,1038
0,132
0,1127
0,7224
0,36
0,2023
0,0982
0,0047
0,141
0,031
0,2473
0,7695
0,0597
0,0271
0,0109
0,0763
0,0416
0,0387
0,1163
0,1557
0,9467
0,1822
0,3576
0,1119
0,3593
0,00101
0
0,00154
0,00083
0
0,0007
0,00079
0,00009
0,0008
0,00053
0,00088
0,06188
0,00939
0,00013
0,00019
0,00194
0,00099
0,00076
0,00185
0,00318
0,01139
0
0,00073
0,00029
0
0,01395
0,00067
0,00069
0,00064
0
0,00426
0
0
0,00872
0
0,00437
0,02558
0,00234
0,002
0,0128
0
0,00346
0,02431
0,00117
0,83917
0,00055
0,00385
0,0104
0,01581
0,00741
0,0186
0,33406
0,00085
0,00072
0,02933
0,04015
0
0,0494
0
0,03039
0
Linha
Transformador
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Transformador
Linha
Linha
Transformador
Linha
Linha
Linha
Linha
Transformador
Linha
Transformador
Transformador
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Transformador
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Transformador
Linha
Transformador
Linha
Transformador
79
230
76
81
234
239
240
242
76
79
249
90
233
243
95
213
214
269
101
86
79
90
101
104
76
81
56
255
29
31
208
44
260
260
42
263
263
47
47
142
95
269
118
271
30
273
65
275
275
28
44
279
279
42
282
282
203
218
223
226
228
27
242
243
243
244
244
244
244
245
245
246
247
248
248
249
249
249
249
250
251
252
252
253
253
254
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
285
286
286
286
287
0,6573
0,0145
0,0214
0,0564
0,3993
0,0643
0,3782
0,0179
0,0764
0,7024
0,034
0,0317
0,0834
0,0672
0,1599
0,1645
0,0082
0,0132
0,0818
0,0937
0,0454
0,0206
0,0309
0,0283
0,0024
0,0186
0,1367
0,4127
0,4276
0,8296
0,9782
0,0845
0,3912
0,9903
0,0763
0,376
0,5408
0,9936
0,4021
0,074
0,4261
0,0588
0,381
0,0591
0,3834
0,2526
0,015
0,1618
0,4083
0,9802
0,0878
0,3962
0,9798
0,0855
0,3892
0,0272
0,0747
0,004
0,6056
0,5392
0,0001
0,0089
0,00345
0,00585
0,00081
0,005
0,00102
0,0051
0,00467
0,01822
0
0,0086
0,00862
0,02055
0
0,0391
0,03821
0
0,00712
0,02018
0,02288
0,01139
0,00542
0,00566
0,00692
0,00054
0,0046
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0,00755
0,02021
0
0,00032
0,00915
0
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Transformador
Linha
Linha
Linha
Transformador
Linha
Linha
Transformador
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Linha
Transformador
Transformador
Transformador
Transformador
Transformador
Transformador
Transformador
Transformador
Transformador
Transformador
Transformador
Transformador
Transformador
Transformador
Transformador
Transformador
Transformador
Transformador
Transformador
Transformador
Transformador
Transformador
Transformador
Transformador
Transformador
Transformador
Transformador
Transformador
Transformador
Linha
Linha
Linha
Linha
Linha
Linha
80
289
29
287
72
90
103
288
289
289
290
291
291
0,0171
0,0001
0,0161
0,0084
0,0001
0,1261
0,03003
0
0,03187
0,00229
0
0,0255
Linha
Linha
Linha
Linha
Linha
Linha
A seguir os dados dos geradores do circuito de 291 barras:
TABELA A.10: REATÂNCIA DOS GERADORES
Barra
2
3
4
5
16
20
22
24
39
41
49
60
103
111
113
115
139
141
171
217
221
223
224
228
230
233
234
237
246
259
261
282
X''d
0,12400
0,20240
1,83330
0,18220
0,05780
0,25251
0,06870
0,07210
1,26270
0,21045
1,26270
1,26270
0,21045
0,16460
0,24700
0,05710
0,21045
0,21045
1,26270
0,21045
1,26270
0,21045
0,21045
0,21045
0,21045
0,21045
0,21045
0,21045
0,21045
1,26270
0,00047
0,21045
X'd
0,186
0,3036
2,74995
0,2733
0,0867
0,378765
0,10305
0,10815
1,89405
0,315675
1,89405
1,89405
0,315675
0,2469
0,3705
0,08565
0,315675
0,315675
1,89405
0,315675
1,89405
0,315675
0,315675
0,315675
0,315675
0,315675
0,315675
0,315675
0,31568
1,89405
0,000705
0,315675
Xd
0,744
1,2144
10,9998
1,0932
0,3468
1,51506
0,4122
0,4326
7,5762
1,2627
7,5762
7,5762
1,2627
0,9876
1,482
0,3426
1,2627
1,2627
7,5762
1,2627
7,5762
1,2627
1,2627
1,2627
1,2627
1,2627
1,2627
1,2627
1,262718
7,5762
0,00282
1,2627