Dinâmica do Sistema Solar

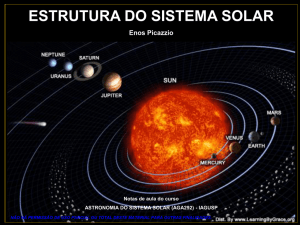
ASTRONOMIA DO SISTEMA SOLAR
Enos Picazzio (IAGUSP 2006)
DINÂMICA DO
SISTEMA SOLAR
NÃO HÁ PERMISSÃO DE USO PARCIAL OU TOTAL DESTE MATERIAL PARA OUTRAS
OUTRAS FINALIDADES.
Até o final do século XVII eram conhecidos:
Mercúrio, Vênus, Terra, Marte, Júpiter e
Saturno.
Urano foi descoberto em 1781, Netuno em 1846
(baseados em previsões teóricas de Adams (1845)
e Leverrier (1846) e Plutão em 1930 (também por
previsões teóricas).
Enos Picazzio – IAGUSP (2006)
O que são planeta, planeta duplo e satélite?
União Astronômica Internacional (IAU)
(Proposta a ser votada)
Planeta: corpo celeste que (a) tenha massa suficiente
para que sua autogravitação supere a rigidez de seu
material e estabeleça o regime de equilíbrio hidrostático
- responsável pela forma aproximadamente esférica -, e
(b) que orbite uma estrela, sem ser estrela ou satélite.
Pela nova classificação, haveria 12 planetas: Mercúrio, Vênus, Terra,
Marte, Ceres, Júpiter, Saturno, Urano, Netuno, Plutão-Caronte e Xena
(2003UB313). Porém, há uma lista de quase uma dezena de candidatos a
planetas.
Um corpo com massa superior a 5×1020 kg (1.400 vezes menor
que a da Lua) e diâmetro mínimo de 800 km (4 vezes menor que
o da Lua) satisfaz essa condição.
Enos Picazzio – IAGUSP (2006)
O que são planeta, planeta duplo e satélite?
União Astronômica Internacional (IAU)
(Proposta a ser votada)
Planeta duplo: quando o baricentro (centro de massa) do
sistema está fora do corpo maior.
O baricentro da dupla Plutão e
Caronte está cerca de 1.200 km
acima da superfície de Plutão.
S/2005P2
S/2005P1
Plutão
Caronte
Diâmetros aproximados em km:
Plutão: 2.400, Caronte:1.200, P1: 60 a 165, P2: 40 a 140
Enos Picazzio – IAGUSP (2006)
http://upload.wikimedia.org/wikipedia/commons/6/65/TheKuiperBelt_Orbits_PlutoQuadSystem.svg
O que são planeta, planeta duplo e satélite?
União Astronômica Internacional (IAU)
(Proposta a ser votada)
Satélite: corpo celeste girando em torno de um
baricentro localizado no interior do planeta que órbita.
Esta condição vale independentemente de o corpo satisfazer a condição
de planeta (massa e diâmetro mínimos).
No caso da dupla Terra e Lua, o baricentro do sistema está cerca de
1.400 km abaixo da superfície terrestre, apesar de a Lua satisfazer a
condição de planeta.
Os baricentros dos satélites Ganimedes (Júpiter) e Titã (Saturno), que
são maiores que Mercúrio, estão fora dos seus planetas.
Enos Picazzio – IAGUSP (2006)
Parâmetros orbitais
Inclinação (i) - é o ângulo formado entre a órbita do
planeta e o plano da eclíptica. Se i > 90º, o corpo
orbita o Sol em sentido contrário ao movimento da
Terra (movimento retrógrado).
Longitude do nodo ascendente (Ω
Ω) - é o ângulo
entre o ponto Vernal (γ) e o nodo ascendente do
corpo. (0 ≤ Ω ≤ 360º)
Argumento do periélio (ω
ω) - é o ângulo, medido
sobre o plano orbital do corpo, entre o periélio P e o
nodo ascendente, contado no sentido do movimento
do corpo.(0 ≤ ω ≤ 360º)
Semi-eixo maior da órbita (a) - distância média do
astro ao Sol.
Excentricidade da órbita (e) - relação entre a semi -distância focal e o semi-eixo maior.
Instante (época) de passagem pelo periélio (t0) - é a época de uma determinada passagem pelo
periélio.
Período sideral (P) - é o tempo necessário para o objeto orbitar uma vez em torno do Sol.
Longitude do periélio (ϖ
ϖ) - é definido como a soma algébrica entre a longitude do nodo ascendente
(Ω) e o argumento do periélio (ω): ϖ = Ω + ω
2π
Movimento médio (n) - é a velocidade angular média do corpo em torno do Sol: n =
P
Enos Picazzio – IAGUSP (2006)
Leis de Kepler
Obtidas empiricamente no século XVII, através da redução das observações de
Tycho Brahe.
Resultados obtidos só foram ajustados a órbitas elípticas.
Enos Picazzio – IAGUSP (2006)
Lei de Gravitação Universal
Galileu Galilei: estudando as leis do movimento procurava a resposta à
pergunta básica: Por que os planetas estão em movimento?
Princípio da Inércia: Se um corpo não for perturbado, permanecerá em MRU.
Newton: Interpretou esse “Princípio” da seguinte maneira:
A única maneira de modificar o movimento de um corpo é utilizar o conceito
de força. Como?
Direção do movimento ≡ Direção da força
Então: deve existir uma “força lateral” , aplicada ao planeta, para mantê-lo em
órbita fechada.
Lei de Gravitação Universal
Problema de 3 corpos
Neste caso existem 5 soluções estacionárias Æ 5 pontos Lagrangianos.
Soluções estáveis: L4 e L5.
Havendo perturbação, o corpo pode voltar à posição de equilíbrio dependendo da
relação entre as massas envolvidas.
Exemplo típico: asteróides Troianos de Júpiter.
Enos Picazzio – IAGUSP (2006)
Planetas: Classificação e Configuração
clássicos
anão
duplo
Ceres
Xena
Enos Picazzio – IAGUSP (2007)
-Caronte
Plútons
Planetas: Classificação e Configuração
clássicos
anão
duplo
(PERUDSUHVHQWHVQDOLWHUDWXUDRVWHUPRV
LQIHULRUHVLQWHULRUHVWHUUHVWUHV
Ceres
VXSHULRUHVH[WHULRUHVMRYLDQRVDQmR
JLJDQWHVVyOLGRVJDVRVRVJHODGRVQmR
VmRWHUPRVRILFLDOL]DGRVSHOD8QLmR
$VWURQ{PLFD,QWHUQDFLRQDO
Xena
Enos Picazzio – IAGUSP (2007)
-Caronte
Plútons
Planetas: Classificação e Configuração
Configurações planetárias
Planetas internos:
I1 - conjunção inferior
I2 - máxima elongação ocidental (O)
I3 - conjunção superior
I4 - máxima elongação oriental (L)
Planetas exteriores:
E1 - oposição
E2 - quadratura ocidental (O)
E3 – conjunção
E4 - quadratura oriental (L)
S – Sol
T – Terra
I – planeta interno
E – planeta externo
Enos Picazzio – IAGUSP (2006)
Planeta Superior
D
d
A – duração do ano ; T – período sideral (orbital) ; S – período sinódico (aparente)
Enos Picazzio – IAGUSP (2006)
Planeta Superior
D
d
A – duração do ano ; T – período sideral (orbital) ; S – período sinódico (aparente)
S ≡ período sinódico entre 2 oposições
S = t( T3 ) − t( T1 ) ⇒ planeta percorreu α
Terra percorreu 360º + α
Para a Terra : 360º → A
360 S
α=
− 360
A
360º + α → S
360 S
Para o planeta : 360º → T
T=
α
α →S
Enos Picazzio – IAGUSP (2006)
1 1 1
= −
T A S
Planeta Superior
D
d
A – duração do ano ; T – período sideral (orbital) ; S – período sinódico (aparente)
Seja t = t( T2 ) − t( T1 )
Intervalo entre uma oposição e quadratura mais próxima :
Para a Terra :
360º → A
360t
α →t
Para o planeta : 360º → T
β →t
Enos Picazzio – IAGUSP (2006)
α=
β=
A
360t
T
Da figura (B) :
d=
D
cos γ
onde γ = α - β
Planeta Inferior
ST1 = ST2 = ST3 = d
SP1 = SP2 = SP3 = D
Distância heliocêntrica do planeta :
D = d senβ
Período sinódico: tempo decorrido entre duas posições
idênticas sucessivas
S = t (T3 ) − t (T1 )
A – duração do ano
T – período sideral (orbital)
S – período sinódico (aparente)
Enos Picazzio – IAGUSP (2006)
t ≡ instantes de elongação máxima
Planeta Inferior
No intervalo de tempo S :
1. Terra deslocou - se de um ângulo "α "
(A ≡ 365,256 d)
∴ 360º → A
α →S
360S
ou α =
A
2. Planeta foi de P1 → P3 , ou deslocou - se de 360º +α
∴
S → 360º +α
ou T =
360 S
360 S
=
360 + α 360 + (360 S / A)
T → 360º
A – duração do ano
T – período sideral (orbital)
S – período sinódico (aparente)
Enos Picazzio – IAGUSP (2006)
logo :
1 1 1
= +
T A S
Mercúrio: período
Período orbital em torno do Sol:
~ 116 d (M1ÆM2ÆM3);
portanto o intervalo entre elongações máximas é
~ 58 d
Terra :
365 d → 360º
58 d → 57º
ˆT )
(T1S
2
Mercúrio :116 d → mesma posição de elong. máx. (M1 , M 3 )
∴ em 116 d descreve 360º +2 x 57º = 474º
então : 474º → 116 d
360º → 88 d *
A – duração do ano
T – período sideral (orbital)
S – período sinódico (aparente)
*
Enos Picazzio – IAGUSP (2006)
1 1 1
1
1
1
= + =
+
= 0.0113636 =
⇒ T = 88 d
T A S 365,256 116
88
Mercúrio: distância relativa
Aproximando a órbita para circular :
a distância heliocêntrica da Terra : ST1 , ST2 , ...
ˆ M = ST
ˆ M = ST
ˆ M ≅ 23º
da observação : ST
1
1
2
2
3
3
ˆ T = SM
ˆ T = SM
ˆ T = 90º
da órbita circular : SM
1 1
2 2
3 3
∴
Enos Picazzio – IAGUSP (2006)
SM1 = ST1 sen23º ≅ 0.39 ST1
4XHWDOID]HUDVSDVVDJHQVGDV
HTXDo}HVQDPmR"
6HUiPDLVGLYHUWLGRTXHLUDXPD
EDODGD
Enos Picazzio – IAGUSP (2007)