Sistemas Numéricos

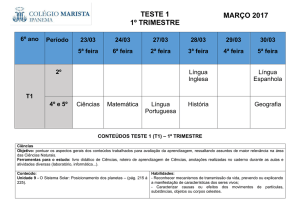
Sistemas Numéricos
Eletrônica Digital
PROFESSOR LUCAS KOEPSEL ROSA
Definição de Sistemas Numéricos
Eletrônica Digital
PROFESSOR LUCAS KOEPSEL ROSA
Definição Sistemas Numéricos

Em condições ideais,
numeração deve:
um
sistema
•
Representar uma grande quantidade de
números úteis (ex.: todos os números
inteiros, ou todos os números reais);
•
Dar a cada número representado uma
única descrição (ou pelo menos uma
representação padrão);
•
Refletir
as
estruturas
aritméticas dos números.
algébricas
de
e
Sistemas Numéricos - Professor Lucas Koepsel Rosa
Definição Sistemas Numéricos

Um sistema de numeração, (ou sistema
numeral) deve possuir:
•
Linguagem representativa dos valores;
•
Alfabeto definido e finito;
•
Sua difusão universal não deve seguir as
leis da matemática.
Sistemas Numéricos - Professor Lucas Koepsel Rosa
Tipos de Sistemas Numéricos

Entre os sistemas numéricos mais utilizados
na
computação
há
o binário, decimal, octal e sistema
hexadecimal.
Cada
um
destes
apresentando sua própria faixa de valores
possíveis, e cada um possui uma aplicação
específica,
dentro
da
Ciência
da
Computação.
Sistemas Numéricos - Professor Lucas Koepsel Rosa
SND – Sistema de Numeração
Decimal

O sistema decimal ou de base dez é um sistema de
numeração posicional em que todas as quantidades se
representam com base em dez números.

Sistema usual de numeração;

Digitos: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9;

Organização posicional: 328 = 3x102 + 2x101 8+x100 = 300 + 20 + 8;

Base 10;

Numeros são expressos como somas de potências de 10 (a base do
Sistema decimal)

Identificação do Sistema empregados em uma numeração : 32810;
Sistemas Numéricos - Professor Lucas Koepsel Rosa
SNB – Sistema de Numeração
Binário

O sistema binário ou de base 2 é um sistema de
numeração posicional em que todas as quantidades se
representam com base em dois números, ou seja, zero e um (0 e 1).

Sistema tipicamente aplicado em sistemas computacionais devido
a correspondência entre os dois estados de sinal digital –
inativo/ativo (off/on, false/true);

Digitos: 0, 1;

Organização posicional: 10101 = 1x24 + 0x23 + 1x22 + 0x21 + 1x20;

Base 2;

Identificação do Sistema empregados em uma numeração :
101012;
Sistemas Numéricos - Professor Lucas Koepsel Rosa
SNO – Sistema de Numeração
Octal

O sistema octal ou de base 8 é um sistema de
numeração posicional em que todas as quantidades se
representam com base em oito números. No ocidente, estes são os
algarismos arábicos.

Digitos: 0, 1, 2, 3, 4, 5, 6, 7;

Base 8;

Identificação do Sistema empregados em uma numeração : 3248;
Sistemas Numéricos - Professor Lucas Koepsel Rosa
SNH – Sistema de Numeração
Hexadecimal

O sistema hexadecimal ou de base 16 é um sistema de
numeração posicional em que todas as quantidades se
representam com base em dezesseis números, portando
empregando 16 símbolos.

Digitos: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F;

As letras de A à F representam respectivamente os números de 10 à
15;

Base 16;

Identificação do Sistema empregados em uma numeração : 3B116;
Sistemas Numéricos - Professor Lucas Koepsel Rosa
Conversão entre Bases de SN´s
Eletrônica Digital
PROFESSOR LUCAS KOEPSEL ROSA
Conversão entre Bases, por quê?

A aplicação de conversão entre bases é importante para melhor
entendimento e comunicação quando representados
numeradores de bases diferentes.

A conversão entre sistemas numéricos é feita com base em
algumas regras e serve para que se obtenha o valor de um
elemento no sistema numérico mais adequado a cada situação.
Sistemas Numéricos - Professor Lucas Koepsel Rosa
Conversão Decimal para Binário




Para realizar a conversão utiliza-se o método
de divisão repetida.
Divisão
Quociente
Resto
1985/2
992
1
Para converter, por exemplo, o número
decimal 1985 em binário deve-se fazer o
seguinte:
992/2
496
0
496/2
248
0
248/2
124
0
Dividir o número decimal por 2. Caso o
resultado seja exato, aquela divisão terá resto
0 (zero), se não for exato terá resto 1 (um).
Esse valor deve ser anotado da direita para a
esquerda ou como explicado abaixo do
exemplo.
124/2
62
0
62/2
31
0
31/2
15
1
15/2
7
1
7/2
3
1
3/2
1
1
1/2
0
1
Deve-se
dividir
o
número
até
que
o quociente da divisão seja igual a 0 (zero).

Resultado: 111110000012
Sistemas Numéricos - Professor Lucas Koepsel Rosa
Conversão Decimal para Binário

Para convertermos o número 25 para base 2, devemos proceder
da seguinte forma:

A cada passo do exercício, é
realizada a divisão do valor
pelo número da base(2).
Sistemas Numéricos - Professor Lucas Koepsel Rosa
Conversão de Numeros Decimais
para Octal

Para converter de decimal para Octal, procede-se do mesmo
modo que na conversão decimal-binário. Basta agora dividir por 8
e não mais por 2.

Para convertermos o número 21710 e 3710 para base 8, devemos
proceder da seguinte forma:
Sistemas Numéricos - Professor Lucas Koepsel Rosa
Conversão de Numeros Decimais
para Hexadecimais

Para converter de decimal para hexadecimal, procede-se do
mesmo modo que na conversão decimal-binário. Basta agora
dividir por 16 e não mais por 2.

Para convertermos o número 22310 e 7610 para base 10, devemos
proceder da seguinte forma:
Sistemas Numéricos - Professor Lucas Koepsel Rosa
Conversão de Numeros Binários
para Decimais

Para convertermos o número 10011011 para base 10, devemos
proceder da seguinte forma:
Sistemas Numéricos - Professor Lucas Koepsel Rosa
Conversão de Numeros Octal para
Decimais

Para convertermos o número 3318 e 458 para base 10, devemos
proceder da seguinte forma:
Sistemas Numéricos - Professor Lucas Koepsel Rosa
Conversão de Numeros
Hexadecimais para Decimais

Para convertermos o número A2F716 para base 10, devemos
proceder da seguinte forma:
Sistemas Numéricos - Professor Lucas Koepsel Rosa