Revisão de números complexos

REVISÃO DE NOTAÇÃO DE NÚMEROS COMPLEXOS
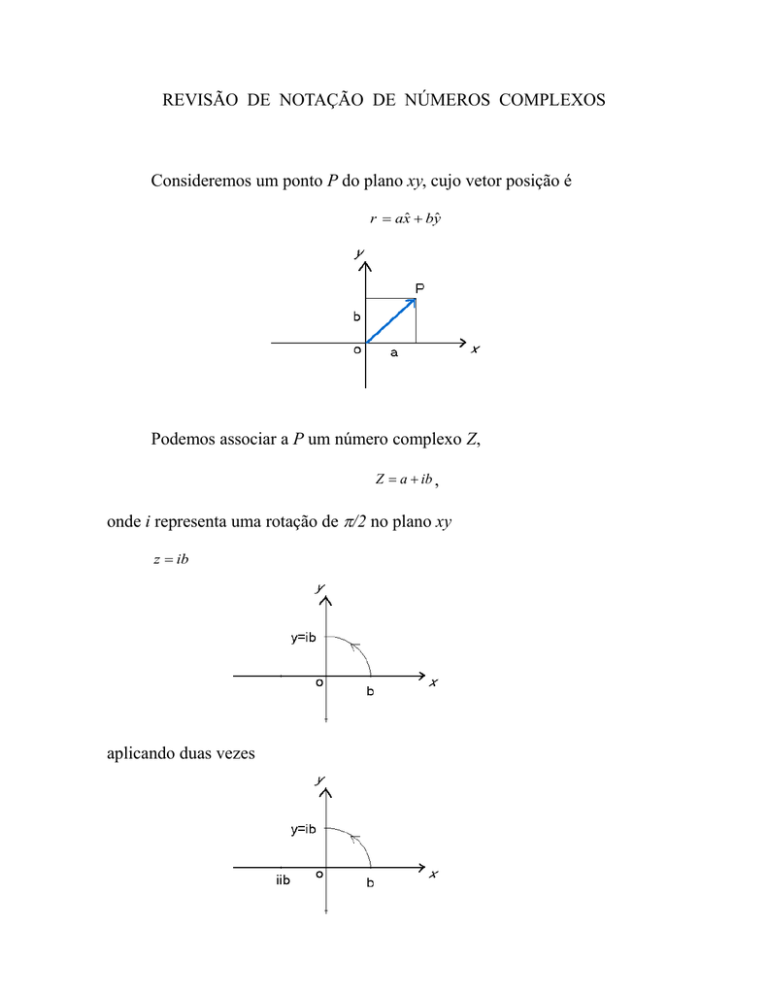
Consideremos um ponto P do plano xy, cujo vetor posição é

r  axˆ  byˆ
Podemos associar a P um número complexo Z,
Z  a  ib ,
onde i representa uma rotação de /2 no plano xy
z  ib
aplicando duas vezes
o que leva a
i
1 ,
o número complexo i chama-se unidade imaginária.
Define-se
a  Re[Z]
z  a  ib 
b  Im[Z]
Propriedades:
a) Soma de números complexos
Z  Z1  Z 2
Z1  a1  ib1
Z 2  a 2  ib2
Z  ( a1  a2 )  i (b1  b2 )
b) Complexo conjugado de um número complexo
Seja o número complexo
Z  a  ib
o seu complexo conjugado é
Z *  a  ib
Assim
1

Z  Z*
2
1
Im[Z ] 
Z  Z * 
2i
Re[ Z ] 
c) Produto entre números complexos
Z  Z1  Z 2
Z1  a1  ib1
Z 2  a2  ib2
Z  (a1  ib1 )(a2  ib2 )  (a1a2  b1b2 )  i (a1b2  b1a2 )
d) Módulo do número complexo
Z 
Z *Z 
( a  ib )(a  ib) 
(a 2  b 2
e) Quociente de dois números complexos
Z
Z1
Z2
Z1  a1  ib1
Z 2  a2  ib2
Z
(a1  ib1 )(a2  ib2 ) a1a2  b1b2
a b ab
 2
 i 2 21 12 2
2
(a2  ib2 )(a2  ib2 )
a2  b2
a2  b2
f) Notação de Euler
Notação polar
Z  re i
Notação retangular
Z  x  iy  r cos   ir sen  ,
sendo
r
x2  y 2  Z
  arctg
y
x
,
onde r é o módulo de Z e  é o seu argumento.
O produto entre dois números complexos nesta notação é
Z  Z1Z 2  r1e i1 r2 e i2
Z  r1r2 e i ( 1 2 )
,
e a divisão fica
Z
Z1 r1e i1 r1 i ( 1 2 )

 e
Z 2 r2 e i2 r2
g) Outras propriedades
 Exponencial de um número complexo
e Z  e ( a ib )  e a (cos b  i sen b)
 Seja 1 e 2 reais e Z1 e Z2 complexos, então
Re[1Z1   2 Z 2 ]  1 Re[ Z1 ]   2 Re[ Z 2 ]
 Se
Z (t )  x(t )  iy (t )
é função de um parâmetro real t, temos
dZ (t ) d
 x(t )  iy(t )   dx(t )  i dy(t )

dt
dt
dt
dt
de modo que
 dZ (t )  d
Re 

Re[ Z (t )]
 dt  dt
o que se estende a derivadas de ordem superior.