física - GOPEM

FÍSICA
PRÉ-VESTIBULAR
LIVRO DO PROFESSOR
Esse material é parte integrante do Aulas Particulares on-line do IESDE BRASIL S/A,
mais informações www.aulasparticularesiesde.com.br
© 2006-2008 – IESDE Brasil S.A. É proibida a reprodução, mesmo parcial, por qualquer processo, sem autorização por escrito dos autores e do
detentor dos direitos autorais.
I229
IESDE Brasil S.A. / Pré-vestibular / IESDE Brasil S.A. —
Curitiba : IESDE Brasil S.A., 2008. [Livro do Professor]
732 p.
ISBN: 978-85-387-0576-5
1. Pré-vestibular. 2. Educação. 3. Estudo e Ensino. I. Título.
CDD 370.71
Disciplinas
Autores
Língua Portuguesa
Literatura
Matemática
Física
Química
Biologia
História
Geografia
Francis Madeira da S. Sales
Márcio F. Santiago Calixto
Rita de Fátima Bezerra
Fábio D’Ávila
Danton Pedro dos Santos
Feres Fares
Haroldo Costa Silva Filho
Jayme Andrade Neto
Renato Caldas Madeira
Rodrigo Piracicaba Costa
Cleber Ribeiro
Marco Antonio Noronha
Vitor M. Saquette
Edson Costa P. da Cruz
Fernanda Barbosa
Fernando Pimentel
Hélio Apostolo
Rogério Fernandes
Jefferson dos Santos da Silva
Marcelo Piccinini
Rafael F. de Menezes
Rogério de Sousa Gonçalves
Vanessa Silva
Duarte A. R. Vieira
Enilson F. Venâncio
Felipe Silveira de Souza
Fernando Mousquer
Produção
Projeto e
Desenvolvimento Pedagógico
Esse material é parte integrante do Aulas Particulares on-line do IESDE BRASIL S/A,
mais informações www.aulasparticularesiesde.com.br
Esse material é parte integrante do Aulas Particulares on-line do IESDE BRASIL S/A,
mais informações www.aulasparticularesiesde.com.br
Esse material é parte integrante do Aulas Particulares on-line do IESDE BRASIL S/A,
mais informações www.aulasparticularesiesde.com.br
Estudo dos
gases e
termodinâmica
Leis dos gases
Consideramos três leis fundamentais:
a)Lei de Boyle ou Lei de Boyle-Mariotte
Este é o tópico de estudo dos gases; nele apresentaremos as características gerais dos gases e as
suas leis clássicas, muitas das quais são objetos de
estudo da química.
Gases
Para sólidos e líquidos, geralmente consideramos
duas variáveis de estado, o volume e a temperatura,
já que trabalhamos praticamente com uma pressão
constante.
Para os gases, entretanto, qualquer pequena mudança na pressão muda o volume de forma significativa;
consideraremos, então, para um gás, três variáveis de estado principais: o volume, a temperatura e a pressão.
Gás perfeito é uma idealização em que são consideradas válidas as seguintes hipóteses:
a)as moléculas estão suficientemente afastadas umas das outras para que não sofram a
ação de forças intermoleculares de coesão;
b)os choques das moléculas entre si e com as
paredes do recipiente que as contém são
perfeitamente elásticos;
c) o movimento das moléculas é caótico, aleatório (movi­mento browniano);
d)o volume das moléculas é desprezível quando
comparado com o volume do recipiente que
as contém.
EM_V_FIS_015
Evolução
Dizemos que um gás sofreu uma evolução quando
ocorre a mudança de, no mínimo, duas das variáveis
de estado; observe que podemos também ter variação
nessas três variáveis de estado.
Experimentalmente, observa-se que, numa
massa gasosa, durante uma transformação feita à
temperatura constante, o produto da pressão pelo
volume é invariável ou P .V = kB (constante de Boyle);
para uma mesma massa gasosa, sofrendo evoluções sempre com a mesma temperatura, podemos
escrever:
P0 V0 = P1 V1 = ... = Pn Vn
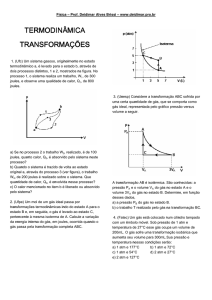
O gráfico representativo dessa lei é:
As curvas são ramos de hipérboles equiláteras
e cada uma é chamada de isoterma ou isotérmica;
no nosso gráfico T2 > T1.
b)Lei de Gay-Lussac
Experimentalmente, observa-se que, em uma dada
massa gasosa, submetida à pressão constante, o volume
é diretamente proporcional à temperatura ou V = kGL
T
(constante de Gay-Lussac); para uma mesma massa
gasosa, sofrendo evoluções sob pressão constante,
podemos escrever:
V0 = V1 = ...= Vn
T0
T1
Tn
Esse material é parte integrante do Aulas Particulares on-line do IESDE BRASIL S/A,
mais informações www.aulasparticularesiesde.com.br
1
Fazendo um gráfico teremos:
A curva representativa é uma reta oblíqua que
passa pela origem se a temperatura for dada em uma
escala absoluta como a escala Kelvin.
c) Lei de Charles
Experimentalmente, nota-se que, em uma determinada massa gasosa, mantido o volume constante, a
pressão de um gás é diretamente proporcional à sua
temperatura ou P = kC (constante de Charles); para
T
uma mesma massa gasosa, sofrendo evoluções sob
volume constante, podemos escrever:
P0
P1
Pn
T0 = T1 = ...= Tn
Fazendo um gráfico teremos:
me Vmol, chamado volume molar e vale 22,4 ; então
P0 Vmol
= R, onde R é a constante universal dos gases
T0
perfeitos ou constante de Clapeyron e tem valores:
atm
ou
R = 0,082
mol K
J
R = 8,31
ou, ainda,
mol K
cal
R 2
.
mol K
Se tivermos um volume qualquer V ele será
sempre nVmol, onde n representa o número de mols;
P0 V
n = R ou
a equação de Clapeyron ficará
T0
P.V = n R T
Transformações gasosas
As principais transformações gasosas são:
a)Transformação isoterma ou isotérmica: é
aquela feita à temperatura constante; obedece à Lei de Boyle ou Boyle-Mariotte, ou seja
P V = kB; o gráfico clássico é o da hipérbole
equilátera, quando colocamos nos eixos os
valores de P e V; menos usual é o gráfico
dessa transformação colocando-se nos eixos os valores de P e T ou V e T; nesse caso,
teríamos uma reta perpendicular ao eixo das
temperaturas.
A curva representativa é uma reta oblíqua que
passa pela origem desde que a temperatura seja dada
em uma escala absoluta como a escala Kelvin.
A equação geral dos gases
Equação de Clapeyron
2
b)Transformação isóbara ou isobárica: é feita
à pressão constante e obedece à lei de GayLussac, ou seja, V = kGL; podemos escrever
T
V = k GL T e trabalhando com a temperatura
em °C, V = k GL ( + 273), obtendo como gráfico
uma reta oblíqua que não passa pelo origem
dos eixos.
Como acabamos de ver, para uma dada massa
PV
gasosa, temos:
= constante.
T
Sabemos que 1mol de qualquer gás, nas CNTP
(condições normais de temperatura e pressão, ou
seja, P0 = 1atm e T0 = 273K ou 0°C) ocupa um voluEsse material é parte integrante do Aulas Particulares on-line do IESDE BRASIL S/A,
mais informações www.aulasparticularesiesde.com.br
EM_V_FIS_015
Podemos associar essas três leis, para a evoluPV
ção de uma mesma massa gasosa, escrevendo 0 0
T0
PV
PV
= 1 1 = ... = n n ,ou seja, a razão P V para uma
T1
Tn
T
mesma massa gasosa é sempre constante.
c) Transformação isócora, isocórica ou isovolumétrica: é feita a volume constante e
obedece à Lei de Charles, ou seja, P = k C;
T
podemos escrever P = kC T e trabalhando
com a temperatura em °C, P = kGL ( + 273),
obtendo como gráfico uma reta oblíqua que
não passa pelo origem dos eixos.
Energia cinética translacional
média das moléculas de um
gás
Imaginemos que num reservatório cúbico, de
aresta d, colocamos uma certa massa de gás, considerando um modelo físico para as moléculas desse gás.
Vamos repassar as condições necessárias para
gás ideal acrescentando algumas condições simplificadoras:
a)todas as moléculas estão em movimento
caótico em todas as direções e sentidos, não
havendo direção preferencial;
b)as colisões das moléculas são perfeitamente
elásticas;
c) entre colisões, a molécula descreve movimento
retilíneo;
EM_V_FIS_015
d)não há forças de coesão apreciáveis;
e) o tamanho das moléculas é desprezível em relação às distâncias percorridas entre colisões;
f) o intervalo de tempo gasto nas colisões é mínimo em relação ao intervalo de tempo entre
colisões.
Consideremos uma molécula, de massa m0, que
acabou de sofrer uma colisão na parede ao lado direito
da caixa, com velocidade média v ; essa molécula vai
se chocar com a parede oposta e, como admitimos
que as colisões são perfeitamente elásticas, vai voltar
com uma velocidade de mesmo módulo; da mecânica
sabemos que o impulso de uma força é igual à
variação da quantidade de movimento, ou seja,
I = Q ou F . t = m0 v ; como estamos admitindo
2d
movimento retilíneo, podemos escrever: t =
v
e calculando o módulo da variação da velocidade
| v | = 2 v ; substituindo na equação do impulso
vem: F . 2d = m0 . 2 v e isolando a força média
v
m
F = 0 . v 2; se dividirmos ambos os termos dessa
d
igualdade por S (área de cada face da caixa) obteremos:
F = m0 .v2; pela definição de pressão (P = Fnormal ) e
S.d
S
S
lembrando que o volume da caixa é V = S . d , vem: m
P0 = 0 v 2; como isso foi feito para uma molécula,
V
apenas para o eixo x e, admitindo que tenhamos
N
m
N moléculas na caixa, teremos: P =
. 0 v 2;
3
V
o produto Nm0 representa a massa total do gás e,
1
m 2
portanto, P =
.
v donde podemos concluir
3
V
que essa expressão nos mostra a pressão exercida
pelas moléculas contra uma parede da caixa.
A massa específica do gás será a massa total
do gás dividida pelo volume total ocupado, ou seja,
Nm0
=
e substituindo na equação anterior teremos:
V
1
. v 2.
P=
3
Usando-se a equação da energia cinétimv 2
ca teremos: Ec =
ou 2 EC =m v 2 , e como
2
1
P V=
. m v 2, por substituição chegaremos a:
3
1
. 2 EC
P V=
3
Esse material é parte integrante do Aulas Particulares on-line do IESDE BRASIL S/A,
mais informações www.aulasparticularesiesde.com.br
3
EC =
3
nRT
2
equação que representa a energia cinética média das moléculas do gás; nessa equação aparece
a constante universal dos gases, já vista no tópico
anterior, e cujos valores podem ser escritos
atm .
R = 8,31J/mol K = 0,082
mol . K
A partir dessa expressão da energia cinética média vamos calcular a velocidade translacional média
quadrática das moléculas:
m
m 2
3
nRT = v ; como n =
EC =
M
2
2
2
3 m
m
3RT
. .RT= v ou v 2.=
e, portanto,
2 M
2
M
v =
3RT
M
o que nos mostra que a velocidade translacional
média quadrática das moléculas é função da temperatura termodinâmica (T) e da natureza do gás (M).
Energia cinética translacional
média por molécula de um
gás
Vamos calcular, agora, a energia cinética média
de cada molécula de um gás; para N moléculas, a
energia cinética de cada uma delas será a energia
cinética total dividida pelo número de moléculas
3
EC
ou ec =
e por substituição: ec = 2 nRT ; o
N
N
número de Avogadro, que representa o número de
moléculas existente em um mol do gás é dado por:
N
N
e, então, n =
o que nos permite escreNA =
n
NA
3
R
R
ver: ec =
.
. T; chamando à razão
de k
2
NA
NA
(como R é uma constante e NA é constante, k será
constante), teremos
ec =
3
kT
2
essa expressão nos mostra que a energia cinética translacional média de uma molécula de um gás
é função única e exclusiva da sua temperatura termodinâmica, o que vem corroborar a ideia expressa
no conceito de temperatura.
4
A constante k é chamada de constante de Boltzmann e como conhecemos os valores de R e NA , para
R
8,31
o SI, podemos escrever: k =
ou k =
NA
6,02 . 1023
k = 1,38 . 10– 23J/K
Massa específica dos gases
Como um gás é definido em função de suas
variáveis de estado, convém definirmos a massa
específica dos gases em função dessas variáveis.
O conceito de massa específica é, sempre, a
relação entre a massa e o volume; da equação de
Clapeyron, PV = nRT, podemos escrever substituindo
m
o número de mols por
:
M
PV=
m
PM
m
RT ou
=
e, portanto:
M
RT
V
=
PM
RT
Calores específicos dos
gases
No estudo da calorimetria, definimos o calor
específico de uma substância; como para os gases,
diferentemente de sólidos e líquidos que trabalhamos com uma pressão constante, a pressão é uma
das variáveis de estado, devemos considerar dois
calores específicos: um sob pressão constante (cP) e
outro sob volume constante (cV).
Verifica-se que cP > cV , existindo uma relação
constante entre esses calores específicos; essa relação
é chamada expoente de Poisson ou Relação de Poisson
e pode ser escrita:
=
cP
cV
Calor específico molar
Chamamos calor específico molar ao produto
do mol pelo calor específico do gás; para pressão
constante teremos CP = McP e para volume constante
c
CV = McV; observa-se facilmente que = P .
cV
Podemos então, lembrando que Q = m c , pensar para os gases em dois calores:
a)Sob pressão constante: nesse caso,
QP=m cP e como m = n M, QP= n M cP ;
substituindo M cP por CP , vem QP= n CP .
Esse material é parte integrante do Aulas Particulares on-line do IESDE BRASIL S/A,
mais informações www.aulasparticularesiesde.com.br
EM_V_FIS_015
Lembrando que, pela equação de Clapeyron,
1
PV = nRT, podemos escrever: nRT=
. 2EC ou
3
b)Sob volume constante: nesse caso,
QV=m cV
e como m = n M, QV= n M cV ;
substituindo M cV por CV , vem QV = n CV .
Q
É facil demonstrar que = P .
QV
Equipartição de energia
Se aquecermos um gás sob pressão constante,
podemos ter aumentos:
a)na energia cinética translacional ( ET), que
causa aumento da temperatura;
b)na energia cinética rotacional ( ER);
c) na energia cinética interna, pelo trabalho, por
exemplo, contra as forças intermoleculares
( Ei);
d)no trabalho realizado na expansão externa
do gás (P V).
Se fizermos o aquecimento sob volume constante,
podemos ter aumento:
a)na energia cinética translacional ( ET), que
causa aumento da temperatura;
b)na energia cinética rotacional ( ER).
O expoente de Poisson pode, então, ser escrito
como:
ET + ER + Ei + P V
=
ET + ER
O valor de Ei é muito pequeno comparado aos
demais, podendo ser desprezado; pela equação de Clapeyron o produto P V, para um mol e variação unitária
de temperatura, será P V = 2cal (constante).
Chamando-se grau de liberdade de um movimento
ao número de coordenadas independentes que são
requeridas para especificarmos esse movimento,
verificamos que, para um gás monoatômico, que
tem três graus de liberdade translacionais (x, y e z),
o ET é igual a 3, o ER é igual a zero e, portanto, o
valor de será:
3 + 0+ 0 + 2
5
=
=
= 1,67.
3+0
3
Para um gás diatômico, que tem três graus de
liberdade translacionais (x, y e z) e dois graus de
liberdade rotacionais, o ET é igual a 3, o ER é igual
a 2 e, portanto, o valor de será:
3 + 2+ 0 + 2
7
=
= 1,40
5
3 +2
Primeiro Princípio
da Termodinâmica
Consideremos um cilindro provido de um pistão
móvel, que pode deslizar sem atrito, contendo um
gás em seu interior; quando aquecemos o gás, ele se
expande e realiza um trabalho sobre o pistão; admitido
que, quando fornecemos calor a uma substância ocorre
um aumento de sua energia interna, podemos escrever
U = Ufinal – Uinicial; o ganho líquido de energia pode
ser expresso por
U=Q–W
expressão conhecida como 1.ª Lei da Termodinâmica.
Para ela adotamos uma convenção de sinais:
Q > 0 quando fornecemos calor para o gás;
Q < 0 quando o gás fornece calor ao meio
exterior;
W > 0 quando o gás realiza um trabalho
(expansão);
W < 0 quando realizamos trabalho sobre o gás
(contração).
Relação de Mayer
Se considerarmos 1mol de gás se expandindo,
a pressão constante, teremos: QP = CP T; a variação de energia interna, sob volume constante, será
U = QV = CV T; substituindo-se esses valores na
1.ª Lei, teremos: CV T = CP T – P V; pela equação de Clayperon, vem: P V = R T e, portanto,
CV T = CP T – R T ou dividindo-se todos os termos
por T, R = CP – CV, que é chamada Relação de
Mayer.
EM_V_FIS_015
=
Para um gás poliatômico, que tem três graus de
liberdade translacionais ( x, y e z ) e três graus de liberdade rotacionais, verifica-se que o modelo teórico
se afasta muito dos resultados experimentais.
Notamos então que, independente da natureza
do gás, os gases monoatômicos terão = 1,67, os diatômicos terão = 1,40 e os poliatômicos não podem
ser analisados adequadamente apenas com a teoria
apresentada anteriormente.
Esse material é parte integrante do Aulas Particulares on-line do IESDE BRASIL S/A,
mais informações www.aulasparticularesiesde.com.br
5
Trabalho na
evolução de um gás
Admitida a expressão geral do trabalho de uma
força constante na mesma direção do deslocamento,
podemos descrever W F . d, e pela definição de pressão F P . S. Assim, substituindo a força na equação de
trabalho, teremos W P . S . d e, por fim,
W P.V
Se fizermos, então, um gráfico Px V, a área sob
a curva vai representar, sempre, o trabalho.
Gráficos de trabalho na
evolução gasosa
Vamos considerar as transformações gasosas já
estudadas:
a) na transformação isóbara (pressão constante):
A área hachurada representa o trabalho realizado sob pressão constante P, na variação de volume
entre V1 e V2; se considerarmos V1 o volume inicial
e V2 o volume final, o trabalho será positivo; caso
contrário, ele será negativo.
b)na transformação isócora, isocórica ou isovolumétrica (volume constante):
A área hachurada representa o trabalho realizado sob temperatura constante T, na variação de
volume entre V1 e V2; se considerarmos V1 o volume
inicial e V2 o volume final, o trabalho será positivo;
caso contrário, ele será negativo. Através do cálculo
integral podemos calcular a área sob a curva como
sendo: W = p1V1lr V2 ou W = p2V2lr V2 , admitindo-se,
V1
V1
nesse caso, uma expansão de V1 para V2.
Podemos agora, com o auxílio dos gráficos, entender melhor a Relação de Mayer.
No gráfico ( I ) vamos de um ponto A, da isoterma
T para um ponto C da isoterma T + T por um processo isobárico. A quantidade de calor envolvido será
QP = n CP T e, aplicando-a na 1.ª lei, teremos:
QP – W = U, onde W é a área sob AC.
No gráfico ( II ) vamos de um ponto B, da isoterma T, para o mesmo ponto C da isoterma T + T, mas
agora por um processo isocórico. A quantidade de calor
envolvida será QV = n CV T e, aplicando-a na 1.ª lei,
teremos: QV – W = U.
Nesse caso, o trabalho é nulo (QV = U), e sendo
U igual nos dois casos, podemos igualar, tendo então:
QP – W = QV ou QP – QV = W. Da equação de Clapeyron
vem: p V = n R T = W e substituindo na equação
anterior teremos n CP T – n CV T = n R T, dividindo
todos os termos por n T implica: CP – CV = R.
A área agora é nula, isto é, numa transformação
isócora não há trabalho executado.
c) na transformação isotérmica (temperatura
constante):
6
Chamamos transformação adiabática àquela na
qual a quantidade de calor trocado com o meio exterior
é nula.
Esse material é parte integrante do Aulas Particulares on-line do IESDE BRASIL S/A,
mais informações www.aulasparticularesiesde.com.br
EM_V_FIS_015
Transformação adiabática
Obedece à Lei de Poisson-Laplace:P 0 V 0
= P V , onde é o expoente de Poisson, já definido
no tópico anterior.
Essa transformação pode ser conseguida variando
rapidamente o volume com a pressão, como acontece
numa bomba de encher pneu de bicicleta.
Vamos voltar a usar a equação geral dos gases:
P0V0
PV
P0 V0 T = P V T0, dividindo membro
T0 = T
a membro a expressão de Poisson-Laplace por esta
PV
PV
teremos P 0V 0T = P V T , e eliminando-se os termos
0 0
0
comuns no numerador e no denominador, vem:
-1
V0 -1
T
T
V0 -1
V -1
V0
=
ou
= T ; como
-1 =
T0
V
T
T0
V
0
é sempre maior que 1, o termo –1 será obrigatoriamente positivo, o que significa que os volumes
são inversamente proporcionais às temperaturas.
Um exemplo prático disso é o “spray”. Quando
pegamos uma lata de “spray”, notamos que está
em temperatura ambiente e, portanto, seu líquido
também. Quando abrimos a válvula, o líquido expelido sai “gelado”; evidentemente trata-se de uma
expansão adiabática: quando abrimos a válvula
provocamos uma expansão (aumentamos o volume)
e como o volume e a temperatura, nesse processo,
são inversamente proporcionais, a temperatura
sofrerá um abaixamento.
Mostramos, a seguir, o gráfico P x V da transformação adiabática (linha cheia) e para comparação colocamos uma isoterma (linha pontilhada).
Observe que a curva isotérmica é mais suave,
enquanto que a curva adiabática varia mais bruscamente, é mais inclinada.
No ciclo, representado no gráfico acima, fizemos
primeiro uma transformação isócora, depois uma
isóbara seguida de uma isotérmica e novamente
uma isóbara.
Quando o ciclo é efetuado no sentido horário,
temos transformação de calor em trabalho (máquina
térmica); quando o ciclo é efetuado no sentido anti-horário temos transformação de trabalho em calor
(refrigerador).
b)Transformação aberta ou não cíclica
Dizemos que um sistema realiza uma transformação aberta quando as variáveis de estado na situação final não coincidem com as do estado inicial.
No ciclo representado no gráfico anterior fizemos, primeiramente, uma transformação isócora, para
depois uma isóbara seguida de uma isotérmica.
c) Transformação reversível
Se ao passarmos de uma posição A, definida
por PA, VA e TA, para outra B, definida por PB, VB e
TB, passamos por estados intermediários de equilíbrio bem definidos, chamamos a transformação de
reversível.
Transformações
EM_V_FIS_015
Podemos classificar as transformações como:
a)Transformação fechada ou cíclica
Dizemos que um sistema realiza uma transformação cíclica quando, partindo do estado inicial definido por P0, V0 e T0, sofre uma série de transformações
intermediárias e volta ao mesmo estado inicial.
d)Transformação irreversível
Se ao passarmos de uma posição A, definida
por PA, VA e TA, para outra B, definida por PB, VB e TB,
não passamos por estados intermediários de equilíbrio bem definidos, chamamos a transformação de
irreversível.
Esse material é parte integrante do Aulas Particulares on-line do IESDE BRASIL S/A,
mais informações www.aulasparticularesiesde.com.br
7
quina a vapor, pois por ele se conclui que o rendimento
depende da diferença entre as temperaturas da fonte
quente e da fonte fria, sendo independente da natureza
do agente que aciona a máquina; nas máquinas a vapor,
portanto, o que importa é aumentar a diferença entre
as temperaturas, não interessando a substituição do
vapor d’água por qualquer outro agente.
Segundo Carnot: “Só é possível a transformação
de calor em trabalho aproveitando-se a diferença
entre as temperaturas de uma fonte quente e uma
fonte fria. O rendimento dessa transformação é
independente da natureza do agente empregado e
só depende da diferença entre as temperaturas das
duas fontes.”
O mesmo princípio foi formulado por Clausius:
“Sem fornecimento de trabalho, é impossível tirar
calor de uma fonte quente e fornecê-lo à fonte fria“.
Também Kelvin formulou um enunciado para
esse segundo princípio: “É impossível realizar uma
transformação em que o único objetivo é converter
em trabalho toda a quantidade de calor cedida por
uma fonte de calor sob temperatura constante”.
Pelo segundo princípio, concluímos que é impossível a transformação integral de uma quantidade
de calor em trabalho, pois a máquina térmica empregada na transformação deve funcionar em contato
com uma fonte fria, que receberá uma parte do calor
fornecido pela fonte quente. Por isso, considera-se
o calor uma forma inferior de energia, ou energia
degradada; como em todas as transformações energéticas há produção de calor, dizemos então que há
degradação da energia, o que justifica a denominação
também dada a esse princípio: Princípio da Degradação da Energia.
Dele também concluímos a impossibilidade do
movimento contínuo ou movimento perpétuo de 2.a
classe, isto é, da construção de um dispositivo que
funcionasse perpetuamente à custa de um suprimento
inicial de energia. Com efeito, em virtude da produção
de calor, tornar-se-ia impossível a transformação
integral desse calor em energia mecânica utilizável pelo
dispositivo para prosseguir em funcionamento.
O 2.º Princípio muito contribuiu para o aperfeiçoamento das máquinas térmicas, em particular da má-
8
O conceito básico de rendimento é, sempre, o
que se ganha naquilo que se aplica.
Rendimento de uma máquina ou motor térmico
é a razão entre o trabalho produzido e o consumo.
Sabemos que o calor fornecido pela fonte quente
(Qquente) será parcialmente convertido em trabalho,
passando para a fonte fria (Qfria) uma quantidade
de calor; a porção transformada em trabalho foi:
Qquente – Qfria, isto é, o trabalho produzido pela máquina
foi: W = Qquente – Qfria.
Então: Wútil = Qquente – Qfria
Q
– Qfria
e, portanto: = quente
ou
Qquente
=1 –
Qfria
Qquente
Ciclo de Carnot
Carnot constatou que, em um ciclo reversível teórico constituído de duas transformações isotérmicas
intercaladas por duas transformações adiabáticas, o
rendimento era máximo.
Através do cálculo do calor e do trabalho envolviQ
Q
do em cada trecho do ciclo verifica-se que 1 = 2 ,
T2
T1
ou seja, existe nesse ciclo uma relação constante entre
a quantidade de calor e a temperatura termodinâmica;
Q1 e T1 referem-se à fonte fria enquanto Q2 e T2 referem-
Esse material é parte integrante do Aulas Particulares on-line do IESDE BRASIL S/A,
mais informações www.aulasparticularesiesde.com.br
EM_V_FIS_015
Segundo Princípio da
Termodinâmica ou
Princípio de Carnot
Rendimento de uma
máquina térmica
Qfria
Tfria
=
e, portanto:
Tquente
Qquente
T
T
–T
=1 – fria ou ainda = quente fria .
Tquente
Tquente
Como sabemos que é impossível um rendimento igual a 1 ( = 100%), isso significa que, a
T
fração fria é, obrigatoriamente, diferente de zero
Tquente
e, portanto, T fria 0, isto é, é impossível atingir o
zero termodinâmico.
se à fonte quente, logo
Entropia
Chamamos entropia (S) de um sistema à grandeza cujas variações exprimem a maior ou menor
possibilidade de transformação da energia do sistema em trabalho mecânico, isto é, a entropia mede a
degradação termodinâmica de um processo reversível ou irreversível
S=
A unidade SI é
Q
T
J
cal
, mas também é usual
.
K
K
EM_V_FIS_015
Variação da entropia
Quando se calculam as variações da entropia
em uma transformação, verifica-se que a entropia do
sistema mais o meio exterior sempre aumenta ou, na
melhor das hipóteses, permanece igual.
Concluímos que, em todas as transformações
com variação de entropia, tal variação, considerandose o conjunto formado pelo sistema mais o meio
exterior, é sempre um aumento, não havendo transformação em que a entropia decresça; por outro lado,
verifica-se que o aumento da entropia coincide sempre com a diminuição da possibilidade de conversão
da energia em trabalho e, portanto, o aumento da
entropia corresponde a uma degradação de energia.
Todas as transformações naturais tendem ao equilíbrio térmico com aumento da entropia; embora a
quantidade total de energia permaneça invariável,
a sua capacidade de utilização diminui e a “morte
térmica” do universo poderá ser o resultado final
dessa degradação.
Podemos, assim, em aditamento ao Segundo
Princípio da Termodinâmica, acrescentar uma proposição com o seguinte enunciado: em todas as
transformações a entropia do conjunto sistema mais
meio exterior sofre um aumento (ou conserva-se
constante), não havendo transformação na qual a
entropia total decresça.
Máquinas térmicas e
máquinas frigoríficas
Vamos considerar dois tipos de máquinas:
aquelas que transformam calor em trabalho (ciclo no
sentido horário) e aquelas que transformam trabalho
em calor (ciclo anti-horário).
Máquinas de ciclo horário
Também são chamadas máquinas térmicas.
Vamos mostrar duas categorias:
I. Máquina a vapor: aproveita a força elástica
do vapor de água superaquecido para impulsionar um pistão em um cilindro, com movimento periódico e alternativo, que é depois
transformado em movimento de rotação. Os
elementos essenciais da máquina são:
a) O gerador de vapor, ou caldeira, onde a água
é vaporizada por aquecimento: nas máquinas móveis utilizam-se as caldeiras tubulares,
nas quais a água circula no interior de tubos
aquecidos pela fornalha. As caldeiras levam
acessórios diversos, como manômetros, válvulas de segurança e indicadores de nível.
b) O cilindro, no qual se desloca o pistão: o
vapor penetra no cilindro por meio de uma
caixa de distribuição ou gaveta, atuando o
vapor ora sobre uma, ora sobre outra face do
pistão. O movimento retilíneo da haste do
pistão é transmitido ao eixo de rotação da
máquina, por meio de órgãos transmissores:
biela e manivela.
c) Após sua expansão no cilindro, o vapor deve
ser expelido para a atmosfera ou para o condensador, que atua como fonte fria.
A máquina a vapor segue, teoricamente, o ciclo
de Rankine.
II.Motor a explosão: aproveita a força expansiva dos gases de uma mistura inflamável
submetida a uma explosão. Trabalha, geralmente, com quatro tempos:
Esse material é parte integrante do Aulas Particulares on-line do IESDE BRASIL S/A,
mais informações www.aulasparticularesiesde.com.br
9
a)Aspiração: no motor a gasolina ou a álcool, a
mistura do combustível com ar, processada
pelo carburador, entra pela válvula de admissão, ficando fechada a de escapamento;
no caso do motor a diesel, o ar é introduzido
no cilindro.
b)Compressão: o pistão comprime a mistura inflamável nos motores a gasolina ou a álcool e ar
no motor a diesel.
c) Explosão: uma faísca elétrica, deflagrada pela
vela, provoca a explosão da mistura nos motores a gasolina e a álcool. No motor a diesel,
o óleo diesel (combustível), que é injetado por
uma válvula no cilindro, explode ao encontrar
ar superaquecido. Os gases resultantes da
explosão impelem o pistão.
e=
Qfria
W
e como W = Qquente – Qfria, vem:
e=
Qfria
Qquente – Qfria
O esquema básico de funcionamento de um
refrigerador é:
d)Escapamento: a válvula de escapamento se
abre e o pistão expele os resíduos para a atmosfera.
– Ciclo Diesel para motor a diesel:
Máquinas de sentido
anti-horário
10
Também chamadas de máquinas frigoríficas.
São representadas pelos refrigeradores. Aqui não
devemos usar o rendimento, mas sim a eficiência.
Definimos a eficiência de uma máquina frigorífica, como a razão entra a quantidade de calor
recebida da fonte fria e o trabalho realizado sobre o
sistema, ou seja,
A é um compressor, acionado por um motor elétrico, que comprime o gás liquefeito (amônia, bióxido
de enxofre, freon etc.), submetendo-o a uma pressão
alta; o gás passa por uma serpentina de refrigeração
B, do lado de fora da geladeira (radiador), ainda sob
alta pressão; C é uma válvula que provoca a expansão
do gás, diminuindo a sua pressão; a serpentina D, localizada dentro da geladeira, promove a vaporização
do gás por absorção do calor do ar e dos alimentos
dentro da geladeira; o gás será novamente liquefeito
e comprimido pelo compressor, retomando o ciclo.
1. (Cesgranrio) Numa primeira experiência, determinada
massa m de um gás perfeito encontra-se no estado
definido pelos valores P, V e T da pressão, do volume
e da temperatura, respectivamente. Numa segunda experiência, uma massa 1/2m do mesmo gás encontra-se
no estado definido pelos valores 1/3P da pressão, e 2V
do volume. Nessa segunda experiência, a temperatura
do gás é:
a) 1/2T
b) 2T
c) 1/3T
d) 3/4T
e) 4/3T
Esse material é parte integrante do Aulas Particulares on-line do IESDE BRASIL S/A,
mais informações www.aulasparticularesiesde.com.br
EM_V_FIS_015
Vemos, assim, que apenas um dos quatro tempos se destina à ação motora. Nos motores de dois
tempos juntam-se as etapas a) e b) no 1.º tempo, e
as etapas c) e d) no 2.º tempo.
Os ciclos teóricos para esses motores são:
– Ciclo de Otto para motor a gasolina ou a álcool:
``
Solução: E
VA
5x1=5
Como houve variação da massa gasosa vamos usar a
m
equação de Clapeyron P V = nRT; como n = mol vem,
m
RT e
para a 1.ª situação P V =
mol
m
P
2
RT’;
para a 2.ª situação 3 2V =
mol
dividindo-se membro a membro essas duas expressões
VB
4x2=8
VC
3x3=9
VD
2x4=8
VE
1x5=5
3
4
T
T’ =
T
teremos 2 = 2
3
T’
2. (Cesgranrio) Leva-se determinada massa de um gás
(suposto perfeito) de um estado inicial A a um estado
final B, representados no gráfico PV abaixo. Nessa
transformação, os estados intermediários são representados pelos pontos do segmento AB.
Vemos que, como o maior produto PV é para o ponto C,
a maior temperatura será a do ponto C.
3. (Cesgranrio) Dois recipientes (I e II na figura abaixo),
de volumes respectivamente iguais a V e 2V, são
interligados por um tubo de volume desprezível,
provido de uma válvula S. Inicialmente, com a válvula
S fechada, o recipiente I contém um gás perfeito
à pressão P0, e o recipiente II está vazio. A seguir,
abre-se a válvula S.
No decorrer da transformação, a temperatura do gás
será máxima quando o volume (em unidades arbitrárias)
for:
a) 1
Sabendo-se que a temperatura final do gás nos dois
recipientes é igual à sua temperatura inicial, podese afirmar que a pressão final do gás no recipiente
II será:
a) P0
b) 2
c) 3
d) 4
b) 2P0
e) 5
``
c) 1/2P0
Solução: C
d) 3P
e) 1/3P0
EM_V_FIS_015
``
Como a massa gasosa é sempre a mesma, podemos
P V
PV
usar a equação geral dos gases: PAVA = B B = C C
TC
TB
TA
P V
= D D = PEVE = constante.
TD
TE
Se essa fração é constante, então T será máxima quando o
produto PV for máximo: fazendo portanto para cada ponto:
Solução: E
A mesma massa gasosa que ocupa o reservatório
1 antes da abertura da válvula, vai ocupar os dois
reservatórios após a abertura da mesma; trata-se de
uma evolução com temperatura constante, o que
significa que podemos usar a Lei de Boyle ou P0 V0 =
P V; chamamos a atenção para este exercício porque
é comum, no cotidiano, pensar-se algo indevido:
quando um pneu de um carro fura, a sua pressão vai
a zero? Não, ele fica com a pressão atmosférica; neste
exercício, quando se abre a válvula, o gás sai Todo
do reservatório I e vai para o reservatório II? Não, ele
passa a ocupar os dois reservatórios, isto é, o volume
final ocupado pelo gás é 3V; teremos, então, P0V =
P3V ou P = 1/3P0 .
Esse material é parte integrante do Aulas Particulares on-line do IESDE BRASIL S/A,
mais informações www.aulasparticularesiesde.com.br
11
4. (FAC. NAC. MED.) Aquece-se certa massa de gás ideal
a volume constante de 27°C a 127°C. Sendo e a energia
cinética média por molécula a 27°C e e’ a 127°C, determine a relação e .
e’
`` Solução:
Como a questão pede a energia por molécula usamos: para 27°C, e = 3 k (27 + 273) e para 127°C,
2
e’ = 3 k (127 + 273); dividindo membro a membro
2
27 + 273
essas duas expressões, teremos e =
127 + 273
e’
e = 300
e = 3 .
e’
400
e’
4
5. (Cescem) Calcule o número de moléculas existentes em
1,0cm3 de gás, à pressão de 1,0atm e à temperatura de
300K.
8. (UFLA) O lavrador, apesar de não saber Física, sabe
que a água conservada em recipiente de barro e não
em vasilhame plástico, mesmo não sendo conservada
em uma geladeira, mantém-se “fresca”; explique por
que, fisicamente.
``
Como o barro é poroso, uma pequena quantidade de
água vai atravessar as paredes e ficar em ambiente
livre; sempre que um líquido está em atmosfera
livre, a qualquer temperatura, ele passa a sofrer
evaporação.
Dados: NA = 6,0 . 1023 moléculas/mol e R = 0,082atm
/mol.K.
Na evaporação, moléculas desse líquido vão passar
para o estado gasoso; evidentemente, as moléculas que
conseguem vencer os obstáculos (tensão superficial,
forças de coesão etc.) são as que possuem maior energia
cinética; se, na totalidade do líquido, as moléculas de
maior energia cinética escapam, sobram as de menor
energia cinética, abaixando, portanto, a energia cinética
média das moléculas do gás; como EC T, diminuindo
EC diminui-se, consequentemente, a temperatura.
Solução:
PVN
Usando Clapeyron PV = nRT e PV = N RT N = RT A
NA
1 . 10 -3 . 6 . 10 23
ou usando os valores dados N =
0,082 . 300
portanto: N = 2,44 . 10 13 moléculas.
6. (PUC) A e B são dois recipientes de volumes iguais
contendo o primeiro m gramas de um gás perfeito
monoatômico e o segundo, 4m gramas do mesmo gás.
Em A, a temperatura é T e a pressão exercida pelo gás
é p. As energias internas das duas quantidades de gás
são iguais. Nessas condições, determine a temperatura
e a pressão em b.
``
Solução:
a) 65
A questão informa ECA = EC , portanto: 3 . m RT
B
2
M
3
4m
=
.
RT’ e simplificando: T’ = T
2 M
4
Aplicando Clapeyron (p V = nRT) para T e para T’:
pV = m RT e p’V = 4m R T , simplificando teremos
M
M
4
p’ = p.
7.
``
12
9. (EsFAO) Determine a quantidade de calor, em cal,
necessária para aquecer de 0°C a 20°C a massa de
5,0g de hélio sob pressão constante, considerando
que o calor específico de hélio sob pressão constante
é cP=1,25cal/g°C.
(PUC) Um recipiente fechado contém o gás monoatômico hélio à temperatura de 300K. É então aquecido a
volume constante e a temperatura final passa a 600K.
Como resultado do acréscimo de temperatura, o que
acontece com a energia cinética média das moléculas
do gás?
Solução:
Usando a equação da energia cinética média das moléculas
vemos que, como 3 , n e R são constantes EC T; se na
2
questão Tf = 2Ti ECf = 2 ECi .
b) 85
c) 105
d) 125
e) 155
``
Solução: D
Sob pressão constante implica QP = m cP T; pelos
valores dados QP = 5 . 1,25 x ( 20 – 0 ) e, portanto,
QP = 125cal
10. (Faap) Aquece-se isobaricamente um gás ideal sob
pressão de 8,3N/m2, temperatura de –23°C e ocupando
um volume de 35m3 até a temperatura de 127°C. Determine o trabalho, em J, realizado no processo.
a) 147,3
b) 174,3
c) 213,7
Esse material é parte integrante do Aulas Particulares on-line do IESDE BRASIL S/A,
mais informações www.aulasparticularesiesde.com.br
EM_V_FIS_015
``
Solução:
d) 254,1
e) 312,5
``
Solução: B
Calculemos, inicialmente, o volume final V0 = V , o
T
T0
V
35
que nos dá:
=
(–23 + 273) (127+ 273)
14. (Elite) Considere um gás perfeito que, sob pressão
de 1atm, ocupa um volume de 16 . Determine a nova
pressão desse gás se ele, sofrendo uma transformação
adiabática, tiver seu volume diminuído para 4 , considerando, por aproximação, que seu expoente de Poisson
é igual a 1,5.
``
Aplicando Poisson-Laplace P0 V0 γ = P V , vem
V = 56m3; como W = p V, substituindo pelos valores
1 . 161,5 = P . 21,5; elevando-se os dois termos ao quadrado
teremos: (1 . 161,5)2 = (P . 4 1,5) 2
dados na questão, teremos: W = 8,3 . (56 – 35) ou
W = 174,3J.
11. (Fac. Nac. Med.) Considere um sistema que recebe 400
calorias de uma fonte térmica, enquanto que, ao mesmo
tempo, é realizado sobre ele um trabalho equivalente a
328J. Qual a variação de energia interna do sistema?
Adote 1cal = 4,18J.
``
Solução:
Como o calor é fornecido ao gás Q = 400cal > 0 e como
o trabalho é executado sobre ele W = 328J < 0; aplicando
a 1.ª lei: ΔU = Q – W e transformando calorias em joules,
vem: ΔU = 400 x 4,18 – (– 328) ou U = 1 672 + 328
U = 2 000J.
12. (FCMSC-SP) Realiza-se um trabalho de compressão
igual a 30J numa transformação de um gás ideal durante
o qual a temperatura não varia. Determinar a variação
de energia interna que sofre o gás e a quantidade de
calor que ele troca no processo.
``
Solução:
3
16
= P 2, portanto, 43 = P 2 ou
4
P = 64, donde: P = 8atm.
ou 163 = P 2 . 4 3
15. (Mackenzie) Para um gás ideal de massa molecular M,
cujos calores específicos à pressão e a volume constante são cP e cV. A partir da Relação de Mayer, podemos
escrever:
1
a) cP M (cV – cP ) =
R
c
b) cV M ( cP – 1) = R
V
c) R M (cP – cV) = cP
d) R M (cV – cP) = cP
e) cP – cV = RM
``
Solução: B
Usando a Relação de Mayer (CP – CV = R) e substituindo
CP por Mcp e CV por M cV , teremos: M cP – M cV = R; coc
locando cV M em evidência, vem: cV M ( cP – 1 ) = R.
Solução:
3
Se a temperatura não varia, T = 0 e como U =
2
nR T
U = 0.
V
Sendo o trabalho realizado contra o gás W = 30J < 0; aplicando-se a 1ª lei: U = Q – W teremos 0 = Q – ( – 30 )
Q = – 30J
13. (EN-adap.) Os cilindros dos motores de um navio a
vapor trabalham com um gás que pode ser considerado ideal, realizando um trabalho de 200J quando
recebem uma quantidade de calor igual a 270cal.
Considere 1cal = 4,2J e calcule a variação da energia
interna do gás, em J.
EM_V_FIS_015
``
Solução:
16. (AFA) Num balão dirigível, um cilindro com êmbolo
móvel contém hélio à pressão do 2,0. 10 4N/m2.
Fornecendo-se 5kJ de calor ao sistema, é registrada
uma expansão de 1,0 . 105cm 3, à pressão constante.
O trabalho realizado e a variação da energia interna
valem em J, respectivamente:
a) 1 500 e 4 500
b) 2 000 e 3 000
c) 2 500 e 2 500
d) 3 000 e 1 000
``
Transformando calorias em joules 270 x 4,2 = 1 134J:
aplicando a 1.ª lei e sabendo que Q > 0 e W > 0,
vem: U = Q – W = 1 134 – 200 = 934J.
Solução: B
Como a pressão é constante, W = P V, e substituindo pelos valores W = 2,0 .10 4 . 105 .10–6, teremos
W = 2,0 . 10 3J; aplicando-se a 1.ª lei U = Q – W, vem:
U = 5 . 103 – 2,0 . 103 = 3 . 103J
Esse material é parte integrante do Aulas Particulares on-line do IESDE BRASIL S/A,
mais informações www.aulasparticularesiesde.com.br
13
17. (Osec) No processo isobárico indicado no gráfico, o gás
recebeu 1 800J de energia do ambiente.
PV
Usando a equação dos gases 0 0 = PV , vem PV
T0
T
T
= 2P . ’ 2V ou T‘ = 4T; como sabemos, a área sob a curva
T
nos dá o trabalho e, sendo a figura um trapézio, teremos:
(2P + P) . (2V – V)
3PV
W=
=
(letra C).
2
2
19. (Cescem) O gráfico representa uma transformação cíclica
em que o sistema passa do estado A ao estado C, pela
transformação ABC, e volta a A pela transformação CDA.
A variação da energia interna do gás foi de:
a) 1 800J
b) 1 200J
c) 1 000J
d) 9 00J
e) 6 00J
``
Solução: E
O trabalho realizado pelo sistema no ciclo ABCDA é
igual a:
a) zero
A área sob a curva nos dá o trabalho, portanto,
W = 30 . ( 60 – 20 ) = 1 200J; pela 1.ª Lei U = Q – W,
e tendo sido dado Q = 1 800J > 0, vem:
b) (P2 – P1) ( V2 – V1 )
c) P1 V1 – P2 V2
U = 1 800 – 1 200 = 600J.
18. (Mackenzie) O gráfico mostra como a pressão P varia
com o volume V quando a temperatura de uma certa
massa gasosa de um gás perfeito se altera.
d) P1 V2 – P2 V1
e) ( P2 + P1 ) ( V2 + V1 )
``
Solução: B
Dado o gráfico de um ciclo, o trabalho é a área interna
da figura; vamos calcular, então, a área de ABCD:
W = (P2 – P1 ) ( V2 – V1 ).
Se a temperatura absoluta inicial é T, então a temperatura
final e o trabalho realizado pelo gás durante o processo
valem, respectivamente:
T
a)
2
b) T e 2PV
c) 4T e 3PV
2
e) 4T e 4PV
``
14
a) O rendimento dessa máquina é igual ao da máquina que executa o Ciclo de Carnot.
b) O rendimento dessa máquina é superado pelo
da máquina que executa o Ciclo de Carnot.
EM_V_FIS_015
d) 2T e 3PV
20. (Cescem) Um inventor informa ter construído
uma máquina térmica que recebe, em um certo
tempo, 10 5 cal e fornece, ao mesmo tempo,
5 x 104cal de trabalho útil. A máquina trabalha entre as
temperaturas de 177°C e 227°C. Nessas condições,
você consideraria mais acertado o seguinte:
Solução: C
Esse material é parte integrante do Aulas Particulares on-line do IESDE BRASIL S/A,
mais informações www.aulasparticularesiesde.com.br
c) A afirmação do inventor é falsa, pois a máquina,
trabalhando entre as temperaturas dadas, não
pode ter rendimento superior a 10% .
d) Mantendo-se as temperaturas dadas, pode-se
aumentar o rendimento, utilizando combustível
de melhor qualidade.
e) Nada do que se afirma anteriormente é correto.
``
Solução: C
Pela equação de rendimento teremos:
5 . 104
=
= 0,5 ou η = 50% para o rendimento des105
sa máquina; o rendimento teórico máximo (ciclo de
227 – 177
= 50 ou = 10%.
Carnot) seria =
227 + 273 500
21. (EN) Uma máquina frigorífica que recebe de uma fonte
calorífica 180kcal, cede ao ambiente 240kcal a cada
minuto. Determine a potência do compressor, em kW,
considerando 1cal = 4,2J.
``
1. (Fuvest) A teoria cinética dos gases propõe um modelo
para os gases no qual:
a) a pressão do gás não depende de velocidade das
moléculas.
b) as moléculas são consideradas como partículas
que podem colidir inelasticamente entre si.
c) a temperatura do gás está diretamente relacionada
com a energia cinética das moléculas.
d) a pressão do gás depende somente do número de
moléculas por unidade de volume.
e) a temperatura do gás depende somente do número
de moléculas por unidade de volume.
2. (Unificado) Uma bola de aniversário, cheia de hélio, é
largada da superfície da Terra, subindo até a altitude de
5 000m. Durante a subida, podemos afirmar que:
Solução:
a) o volume da bola diminui.
W = 60kcal ou W = 60 . 4,2 =
252
W
252kJ; como Pot =
, teremos Pot = 60 ou Pot
t
= 4,2kw.
b) a temperatura da bola aumenta.
W = 240 – 180
c) a pressão do gás no interior da bola aumenta.
d) o volume da bola aumenta.
e) o volume da bola permanece constante.
22. (Elite) Considere um refrigerador que trabalhe com
fonte quente a 37°C e fonte fria a –13°C. Calcule o
calor cedido à fonte quente, considerando que a sua
eficiência é de 50% do refrigerador de Carnot e que
ela recebe 260cal da fonte fria.
``
a) 440K
b) 347K
c) 90K
Solução:
Tquente = 37 + 273 = 310K
Tfria = – 13 + 273 = 260K
T
260
=
eCarnot= T fria– T
310 – 260
quente
fria
eCarnot = 252 = 5,2
60
EM_V_FIS_015
3. (UFF) Um recipiente, feito de um material cujo coeficiente
de dilatação é desprezível, contém um gás perfeito que
exerce uma pressão de 6,00atm quando sua temperatura
é de 111ºC. Quando a pressão do gás for de 4,00atm, sua
temperatura será de:
Como ele opera com 50% de e Carnot teremos:
Q
e refrigerador = 0,5 . 5,2 = 2,6; sendo e = fria e tenW
do sido dado na questão Qfria = 200cal, teremos
260
2,6 =
ou W = 100cal e sabendo-se que
W
W = Qquente – Qfria 100 = Qquente – 260 ou
Qquente = 360cal.
d) 256K
e) 199K
4. (PUC-Rio) Uma bola de soprar está cheia de ar e inteiramente mergulhada na água. Quando retirada de dentro
d’água:
a) seu volume diminui.
b) seu volume aumenta.
c) seu volume permanece inalterado.
d) a densidade do ar dentro da bola aumenta.
e) a massa de dentro da bola diminui.
5. (FOA-RJ) Certa massa de gás ideal ocupa um volume
de 15,0 litros à pressão de 3,00atm. O gás sofre uma
transformação isotérmica e seu volume passa a ser 18,0
Esse material é parte integrante do Aulas Particulares on-line do IESDE BRASIL S/A,
mais informações www.aulasparticularesiesde.com.br
15
litros. A nova pressão dessa massa de gás, em atm, é
igual a:
a) 1,50
d) 586K
e) 595K
b) 3,00
9. (UERJ) Um equilibrista se apresenta sobre uma bola,
calibrada para ter uma pressão de 2,0atm a uma temperatura de 300K. Após a apresentação, essa temperatura
elevou-se para 306K. Considere desprezível a variação
no volume da bola.
c) 5,00
d) 4,00
e) 2,50
6. (UERJ) O vapor contido numa panela de pressão, inicialmente à temperatura T0 e à pressão P0 ambientes, é
aquecido até que a pressão aumente cerca de 20% de
seu valor inicial. Desprezando-se a pequena variação
do volume da panela, a razão entre a temperatura final
T e a inicial T0 do vapor é:
a) 0,8
b) 1,2
c) 1,8
d) 2,0
7.
c) 313K
(Unificado) Um gás ideal passa de um estado A para um
estado B, conforme indica o esquema a seguir:
Calcule a pressão do ar no interior do pneu quando o
equilíbrio térmico com o meio ambiente for restabelecido.
11. (UGF-RJ) Um gás ideal ocupa um volume de 3,0 litros,
quando submetido a uma pressão de 4,0atm. Aumentando-se a pressão para 5,0atm e mantendo-se a temperatura, o volume que ele ocupará, em litros, será de:
a) 2,4
P (atm)
b) 2,8
A
4
Calcule a pressão interna final da bola.
10. (UFRJ) Um pneu de bicicleta é rapidamente inflado
com ar até a pressão de 3,0 atmosferas. No final do
processo, a temperatura do ar no pneu é de 50ºC, enquanto a temperatura no ambiente é de 20ºC. Considere
o volume do pneu constante e o ar nele contido como
um gás ideal.
c) 3,0
B
V ( �)
0
1
e) 4,0
2
Chamando de TA e TB as temperaturas do gás nos estados
A e B, respectivamente, então:
a) TA = TB
12. (EFOA-MG) Um gás perfeito a uma pressão de 10atm,
ocupa um volume de 4 litros. Ele sofre uma transformação isotérmica e seu volume atinge 10 litros. A nova
pressão exercida pelo gás é:
b) TA = 2TB a) 4atm
c) TB = 2TA
b) 25atm
d) TA = 4TB
c) 100atm
e) TB = 4TA
d) 10atm
8. (Unirio) Com base no gráfico abaixo, que representa
uma transformação isovolumétrica de um gás ideal, podemos afirmar que, no estado B, a temperatura é de:
P (N/m2 )
4
2
B
0
a) 273K
b) 293K
20
e) 250atm
13. (PUC-Rio) A pressão de um gás contido num volume V,
à temperatura absoluta T, é determinada pela equação
de estado pV = RT. O número de moléculas existentes
nesse volume é:
a) 1 (um)
A
V ( oC )
16
d) 3,7
b) 6,02 × 1023 mols
c) 1 (um) mol
1
d)
mol
(6,02 × 1023)
Esse material é parte integrante do Aulas Particulares on-line do IESDE BRASIL S/A,
mais informações www.aulasparticularesiesde.com.br
EM_V_FIS_015
1
14. (Unificado) Numa primeira experiência, determinada
massa m de um gás perfeito encontra-se no estado
definido pelos valores p, V e T da pressão, do volume e
da temperatura, respectivamente.
Numa segunda experiência, uma massa 1/2m do mesmo
gás encontra-se no estado definido pelos valores 1/3p
da pressão, e 2V do volume.
Nessa segunda experiência, a temperatura do gás é:
a) 12T
b) 3T
1
c) T
3
3
d) T
4
4
e) T
3
15. (UFCE) A figura abaixo mostra 3 caixas fechadas A, B e
C, contendo, respectivamente, os gases: oxigênio, nitrogênio e oxigênio. O volume de A é igual ao volume de
B e é o dobro do volume de C. Os gases se comportam
como ideais e estão todos em equilíbrio, a uma mesma
temperatura.
A
B
C
17. (Unificado) Um gás ideal evolui desde um estado A até
um estado B, conforme o gráfico a seguir:
P (atm)
B
A
V (litros)
Considere as afirmações:
I. A temperatura do gás aumentou.
II. O gás expandiu-se.
III. A evolução se deu sob pressão constante.
É (são) verdadeira(s):
a) apenas I.
b) apenas III.
c) apenas II e III.
d) apenas II.
e) apenas I e II.
18. (Cesgranrio) Uma certa quantidade de gás ideal se encontra
em equilíbrio termodinâmico no interior de um recipiente
cilíndrico metálico. Esse recipiente é provido de um êmbolo
móvel, sem atrito, de massa m e de secção reta de área A.
Sobre a energia cinética, K , das moléculas em cada uma
das caixas, podemos afirmar:
a) KA = KC < KB
b) KA = KC > KB
c) KA = KB < KC
d) KA = KB = KC
e) KC < KA < KB
16. (UFRRJ) Observe o diagrama abaixo, onde se apresentam duas isotermas T e T’.
a)
P (atm)
T
T‘
3
c
a
b
2
V ( �)
2
EM_V_FIS_015
Nessa situação, o volume ocupado pelo gás é de 5,0L
(figura 1). A seguir, coloca-se um novo êmbolo idêntico
ao primeiro, sobre o conjunto. Restabelecido o equilíbrio,
o volume ocupado pelo gás diminui para 4,0L (figura 2).
A temperatura e a pressão atmosféricas permanecem
constantes no decorrer da experiência. Assim, pode-se
afirmar que a pressão atmosférica vale:
3
mg
As transformações gasosas a, b e c são, respectivamente:
a) isobárica, isotérmica e isocórica.
d) 4
b) isocórica, isobárica e isotérmica.
e) 5
c) isobárica, isocórica e isotérmica.
d) isotérmica, isocórica e isobárica.
e) isotérmica, isobárica e isocórica.
A
mg
b) 2
A
mg
c) 3
A
mg
A
mg
A
19. (Fuvest) Um mol de gás, nas condições normais de
temperatura e pressão, recebem uma quantidade
de calor que, sofrendo uma transformação isobárica, o
Esse material é parte integrante do Aulas Particulares on-line do IESDE BRASIL S/A,
mais informações www.aulasparticularesiesde.com.br
17
20. (UFRJ) Um recipiente de paredes rígidas e isolantes
contém um gás ideal em equilíbrio termodinâmico sob
pressão pe, numa temperatura T. Devido a um defeito na
válvula que controla a entrada e a saída do gás, ocorre
um pequeno escapamento. Reparado o defeito na válvula, verifica-se que o gás restante atinge um novo estado
de equilíbrio sob pressão 0,60p e numa temperatura
0,80T. Que fração do número inicial de moléculas do
gás restou no recipiente?
21. (PUC-Minas) Em um processo a pressão constante de 1,0
× 105 Pa, um gás aumenta seu volume de 9×10-6m3 para
14 × 10-6. m3 O trabalho realizado pelo gás, em joules,
é de:
300K
3mols
2mols
Isolamento
térmico
Mesa
horizontal
Lâmina de cobre
O compartimento da esquerda contém 3mols de gás à
temperatura de 400K, e o da direita, 2mols do mesmo gás
à temperatura de 300K. Dentre as grandezas pressão,
volume, temperatura e densidade, assinale as que terão
o mesmo valor de um lado e de outro do êmbolo, depois
de atingido o equilíbrio termodinâmico entre os dois
compartimentos.
a) pressão, volume, temperatura, somente.
b) pressão, volume, densidade, somente.
a) 0,5
c) pressão, temperatura, densidade, somente.
b) 0,7
d) volume, temperatura, densidade, somente.
c) 0,9
e) pressão, volume, temperatura e densidade.
d) 1,4
e) 2,1
22. (PUC-SP) Você já deve ter notado que, após bater palmas durante algum tempo, suas mãos tornam-se mais
quentes. Esse fato é explicado porque:
a) aumenta a circulação sanguínea, com aumento da
produção de calor.
b) o movimento das mãos pode variar a temperatura
do ambiente, devido ao atrito com o ar.
c) o trabalho mecânico executado pelas mãos se transforma em energia térmica, que varia a temperatura
das mãos.
25. (UFU) Um gás está confinado em um cilindro provido
de um pistão. Ele é aquecido, mas seu volume não é
alterado. É possível afirmar que:
a) a energia interna do gás não varia.
b) o trabalho realizado nesta transformação é nulo.
c) o pistão sobe durante o aquecimento.
d) a força que o gás exerce sobre o pistão permanece
constante.
26. (PUC-Minas) Em uma transformação adiabática, o trabalho realizado por um sistema gasoso é:
a) proporcional ao calor absorvido pelo sistema.
d) durante o movimento as mãos absorvem energia
térmica do ambiente, o que varia sua temperatura.
b) proporcional ao calor cedido pelo sistema.
e) contraria a conservação da energia.
d) sempre nulo, porque a energia interna é constante.
23. (PUC-Minas) Quando a energia interna de um gás aumenta, afirma-se que:
a) a transformação foi adiabática.
b) o sistema realiza trabalho.
c) o sistema troca calor com o ambiente.
d) sua temperatura aumenta.
e) sua temperatura diminui.
24. (Unificado) Um recipiente termicamente isolado do
meio ambiente está dividido em dois compartimentos
estanques por meio de um êmbolo móvel sem atrito,
constituído por uma lâmina de cobre, como mostra a
figura.
18
400K
c) sempre igual à energia interna final do sistema.
e) igual, em valor absoluto, à variação da energia interna.
27. (UFRN) Uma dada massa gasosa sofre uma transformação na qual estão envolvidas transferências de calor
Q, realização de trabalho W e variação de energia ∆U.
Assinale a alternativa correta.
a) Q < W, se a transformação for isotérmica.
b) Q > W, se a transformação for uma expansão isobárica.
c) ∆U = 0, se a transformação for adiabática.
d) ∆U = W, se a transformação for isovolumétrica.
e) Q = 0, se a transformação for isotérmica.
Esse material é parte integrante do Aulas Particulares on-line do IESDE BRASIL S/A,
mais informações www.aulasparticularesiesde.com.br
EM_V_FIS_015
seu volume aumenta de 30%. Determinar a temperatura
final em unidades do SI.
28. (ITA) O diagrama a seguir caracteriza uma transformação
1 → 2 na qual:
II. As transformações ac e bc tem a mesma variação
de energia interna.
III. Na transformação bc, o trabalho é nulo e o sistema
cede calor à vizinhança.
P
2
Entre as alternativas seguintes, assinale opção correta.
a) Somente as afirmativas I e III são verdadeiras.
1
V
b) Somente as afirmativas II e III são verdadeiras.
a) não ocorre variação na energia interna do sistema.
c) Somente as afirmativas I e II são verdadeiras.
b) o sistema não troca calor com o exterior.
d) Todas as afirmativas são verdadeiras.
c) o sistema não realiza trabalho ao passar de (1) para
(2).
e) Todas as afirmativas são falsas.
d) o calor posto em jogo é transformado integralmente
em trabalho.
32. (PUC-Minas) No diagrama pressão x volume de um gás,
a área hachurada representa:
P
e) o sistema recebe calor, que é parcialmente transformado em trabalho.
29. (Unirio) Um gás ideal está submetido a uma pressão de
1,0 . 105N/m2. Inicialmente, o volume é de 1,0 . 10-3 m3,
e sua temperatura é de 27oC. Ele sofre uma expansão
isobárica até que o volume final seja o triplo do volume
inicial. Determine:
a) o trabalho mecânico, em Joules, realizado pelo gás
durante a expansão.
b) a temperatura do gás, em Kelvin, no estado final.
30. (UENF) Considere uma certa quantidade de um gás
ideal em equilíbrio térmico. Sejam Pi e Vi a sua pressão
e seu volume nessa situação. Suponha agora que esse
gás sofra uma expansão isotérmica reversível até atingir um novo estado de equilíbrio, no qual seu volume
vale Vf. Nesse processo, o gás realizou um trabalho Wf.
Caso esse gás tivesse sofrido uma expansão adiabática
reversível, partindo do mesmo estado de equilíbrio inicial
e atingindo um estado final de equilíbrio com o mesmo
volume Vf, o trabalho realizado neste segundo processo
W’f, teria sido maior, menor ou igual a Wf?
Justifique sua resposta.
31. (UFV) Considere as afirmativas abaixo, relativas às transformações de um gás ideal mostradas na figura:
V
a) a energia interna final.
b) a energia interna inicial.
c) o calor absorvido.
d) o trabalho realizado.
33. (Fatec) Um sistema realiza um ciclo ABCDA representado. O trabalho realizado pelo sistema no ciclo vale:
a) 2,0 × 105J
b) 4,0 × 105J
c) 1,0 × 105J
d) 6,0 × 105J
e) 3,0 × 105J
34. (UFRGS) Quando fornecemos 100J de calor a um gás
ideal, ele realiza um trabalho, conforme mostra o gráfico,
indo do estado I ao estado F. Qual a variação da energia
interna do gás para essa transformação?
EM_V_FIS_015
20
I. Na transformação ac, o sistema realiza trabalho e
recebe calor.
10
0
P (Pa)
I
F
v (m³)
123456
Esse material é parte integrante do Aulas Particulares on-line do IESDE BRASIL S/A,
mais informações www.aulasparticularesiesde.com.br
19
a) nula
d) 1,0
b) 20J
e) 0,8
37. (UERJ) Um gás ideal, inicialmente sob pressão P0 e
volume V0, experimenta uma evolução cíclica ABCDA,
como ilustrado na figura abaixo.
c) 80J
d) 100J
e) 80J
P
35. (UFPE) O diagrama PV da figura ilustra a variação da
pressão com o volume durante uma transformação quase
estática e isotérmica de um gás ideal, entre o estado
inicial I e o estado final F.
C
B
3PO
A
PO
D
V
VO
3VO
Calculando-se o trabalho realizado pelo gás no ciclo ABCDA,
encontra-se o valor:
a) 2P0V0
b) 4P0V0
c) 6P0V0
Das afirmativas abaixo:
I. É nula a variação da energia interna do gás nesse
processo.
II. O trabalho realizado pelo gás é numericamente
igual à área abaixo da curva IF.
III. O calor absorvido pelo gás é numericamente igual
à área abaixo da curva IF.
Pode-se afirmar que:
a) apenas I é correta.
b) apenas II e III são corretas.
c) apenas I e II são corretas.
d) todas são corretas.
e) nenhuma é correta.
d) 9P0V0
38. (UFCE) Consideremos um gás ideal contido em um recipiente cilíndrico provido de um êmbolo móvel, que pode
mover-se livremente sem atrito. Partindo do estado A, o
gás sofre as transformações vistas na figura abaixo.
P (N/m 2 )
B
40
30
20
C
A
10
V (m3)
2
4
6
8
Determine o trabalho realizado (em joules) pelo gás no
ciclo A → B → C → A.
39. (UFRJ) A figura representa, num diagrama p×V, dois
processos, mediante os quais é possível fazer um gás
perfeito evoluir entre dois estados de equilíbrio (i) e (f).
36. (UFU) Um gás está submetido a uma pressão constante
dentro de um recipiente de volume variável. Provocandose uma expansão isobárica desse gás, o seu volume
varia, como mostra a figura. Ao passar do estado X para
o estado Y, o gás realiza um trabalho que, em joules, é
igual a:
P (N/m 2 )
isoterma
processo 1
i
processo 2
f
V
Em qual deles foi maior a quantidade de calor envolvida?
40. (Fuvest) O diagrama P × V da figura refere-se a um gás
ideal passando por uma transformação cíclica, através
de um sistema cilindro-pistão.
(P (N/m 2 )
4,10
5
a) 1,6
20
2,10
D
1,5
B
C
V (cm 3 )
4,0
b) 1,4
a) Qual é o trabalho realizado pelo gás no processo AB?
c) 1,2
b) Em que ponto do ciclo a temperatura do gás é menor?
Esse material é parte integrante do Aulas Particulares on-line do IESDE BRASIL S/A,
mais informações www.aulasparticularesiesde.com.br
EM_V_FIS_015
A
5
41. (AFA) O princípio fundamental em que se baseia o termômetro é a(o):
para a fonte fria em cada ciclo e o rendimento do motor
valem, respectivamente:
a) Lei zero da termodinâmica.
a) 400cal e 50%
b) Primeira lei da termodinâmica.
b) 300cal e 25%
c) Segunda lei da termodinâmica.
d) Das trocas de calor sensível e latente.
42. (UFV-MG) As afirmativas abaixo referem-se à Segunda
Lei da Termodinâmica:
I. Nenhuma máquina térmica que opere entre duas
temperaturas dadas pode apresentar maior rendimento que uma máquina de Carnot, que opere
entre as mesmas temperaturas.
II. É impossível qualquer transformação cujo único resultado seja a absorção de calor de um reservatório
a uma temperatura única e sua conversão total em
trabalho mecânico.
III. Uma máquina de Carnot apresenta menor rendimento ao operar entre 10ºC e –10ºC que ao operar
entre 80ºC e 60ºC.
Dentre as afirmações anteriores, são verdadeiras:
a) I e II
c) 600cal e 50%
d) 450cal e 50%
e) 450cal e 25%
45. (UFV) Um folheto explicativo sobre uma máquina térmica
afirma que ela, ao receber 1 000cal de uma fonte quente,
realiza 4 186J de trabalho. Sabendo que 1cal equivale a
4,186J e com base nos dados fornecidos pelo folheto,
você pode afirmar que essa máquina:
a) viola a primeira Lei da Termodinâmica.
b) possui um rendimento nulo.
c) possui um rendimento de 10%.
d) viola a segunda Lei da Termodinâmica.
e) funciona de acordo com o ciclo de Carnot.
46. (AFA) Um gás ideal monoatômico sofre as transformações AB e BC, representadas no gráfico p × V abaixo.
b) I, II e III
p
d) apenas a I
C
p
e) II e III
A
43. (UFBA) A Segunda Lei da Termodinâmica pode ser
encarada como um princípio da degradação da energia
porque:
a) o calor não pode passar espontaneamente de um
corpo para outro de temperatura mais baixa que o
primeiro.
b) para produzir trabalho continuamente, uma máquina térmica, operando em ciclos, deve necessariamente receber calor de uma fonte fria e ceder parte
dele a uma fonte quente.
c) é possível construir uma máquina, operando em ciclos, cujo único efeito seja retirar calor de uma fonte
e convertê-lo em uma quantidade equivalente de
trabalho.
d) é impossível se converter totalmente calor em outra
forma de energia.
e) a Termodinâmica independe de qualquer teoria atômico-molecular.
EM_V_FIS_015
B
2p
c) I e III
44. (Mackenzie) Um motor térmico funciona segundo o
ciclo de Carnot. A temperatura da fonte quente é 400K
e a da fonte fria é 300K. Em cada ciclo o motor recebe
600cal da fonte quente. A quantidade de calor rejeitada
0
V
V
2V
4V
Analisando o gráfico pode-se afirmar que, na transformação:
a) AB, o gás recebe calor do meio externo.
b) BC, a energia interna do gás aumenta.
c) AB, o gás perde calor para o meio externo.
d) BC, a energia interna do gás diminui.
47. (UFRGS) Selecione a alternativa que preenche corretamente as lacunas no parágrafo abaixo, na ordem em que
elas aparecem.
A entropia de um sistema termodinâmico isolado
nunca .......... : se o sistema sofre uma transformação
reversível, sua entropia .......... ; se o sistema sofre uma
transformação irreversível, sua entropia .......... .
a) aumenta - permanece constante - diminui.
b) aumenta - diminui - permanece constante.
c) diminui - aumenta - aumenta.
d) diminui - permanece constante - aumenta.
e) diminui - permanece constante - permanece constante.
Esse material é parte integrante do Aulas Particulares on-line do IESDE BRASIL S/A,
mais informações www.aulasparticularesiesde.com.br
21
48. (UFV) De acordo com a segunda Lei da Termodinâmica,
a entropia do universo:
a)
a) não pode ser criada nem destruída.
P
B
A
C
D
V
b) acabará transformada em energia.
c) tende a aumentar com o tempo.
b)
d) tende a diminuir com o tempo.
50. (UENF) Um gás ideal é levado a realizar as transformações termodinâmicas cíclicas A → B → C → D → A.
O gráfico abaixo representa um ciclo completo dessas
transformações. Baseando-se nos dados fornecidos
pelo gráficos, calcule:
P (103
D
C
B
e) permanece sempre constante.
49. (UFPE) Durante um processo que leva um sistema
termodinâmico de um estado A para outro estado B, o
sistema absorve 16 kJ de calor e realiza 12 kJ de trabalho.
Durante o processo de volta, que leva o sistema de B
até A, o sistema rejeita 18 k J de calor. Qual é o módulo
do trabalho realizado pelo sistema, em kJ, durante o
processo de volta?
P
A
c)
V
P
B
A
C
D
d)
V
P
D
A
C
B
e)
P
V
B
A
D
C
V
2
N/m )
0,3
A
B
D
C
2
4
V (m3)
5
a) o trabalho realizado pelo gás no trecho A → B →
C de um ciclo.
b) o calor trocado por esse gás quando executa 6 000
ciclos.
51. (Cefet-PR) Uma máquina a vapor recebe vapor saturado
de uma caldeira à temperatura de 200ºC e descarrega o
vapor expandido à temperatura de 100ºC (diretamente
no ar atmosférico). Se a máquina operasse segundo o
Ciclo de Carnot, o rendimento máximo seria, em porcentagem, igual a:
a) 50
b) 32
c) 21
d) 43
54. (EN)Uma câmara é vedada por um pistão móvel, que
mantém no seu interior um gás à pressão constante de
100N/m2. Inicialmente o gás encontra-se à temperatura
de 27ºC, ocupando um volume de 150 . Fornecendo-se
50J de calor ao gás, sua temperatura passa a ser de
227ºC e seu volume 250 . A variação da energia interna
do gás durante esse processo foi, em joules, de:
a) 10
e) 10
52. (Unificado) São quatro as etapas do ciclo de funcionamento de uma máquina térmica.
22
53. (Cesgranrio) Certa máquina térmica cilíndrica e reversível
trabalha entre –73ºC e 27ºC. O seu rendimento máximo
é igual a:
2
a) 3
1
b) 3
27
c)
273
3
d)
373
e) todas as respostas anteriores estão erradas.
1.a etapa (A → B): expansão isobárica.
2.a etapa (B → C): expansão isotérmica.
3.a etapa (C → D): contração isobárica.
4.a etapa (D → A): compressão isométrica.
Assinale o diagrama P × V (pressão versus volume)
correspondente a esse ciclo.
b) 20
c) 40
d) 50
55. (UFOP) As figuras seguintes mostram os esquemas
de três máquinas térmicas, sendo T1 a temperatura da
fonte fria, T2 a temperatura da fonte quente, Q1 e Q2 os
módulos das quantidades de calor transferidas entre as
fontes e a máquina, e W o módulo do trabalho.
Esse material é parte integrante do Aulas Particulares on-line do IESDE BRASIL S/A,
mais informações www.aulasparticularesiesde.com.br
EM_V_FIS_015
0,6
A
B
C
T2
T2
T2
Q2
Q2
W
b) No processo b→ c a energia interna do sistema
diminui.
Q2
W
W
Q1
Q1
T1
T1
Afirma-se:
I. O esquema A representa uma máquina possível e o
trabalho que realiza é W = Q2 – Q1.
c) No processo c→ d a energia interna do sistema
diminui.
d) No processo d→a a energia interna do sistema aumenta.
e) No ciclo completo a variação da energia interna é
positiva.
58. (EsPECEx) Certa máquina térmica opera com rendimento de 30%. Se ela realiza um trabalho de 600 joules, o
calor que retira da fonte quente vale:
a) 875W
II. O esquema B representa uma máquina possível e o
trabalho que realiza é W = Q.
b) 2 000J
III. O esquema C representa um refrigerador possível e
o trabalho absorvido é: W = Q2 – Q1.
d) 420J
Assinale a opção correta.
a) Apenas I é verdadeira.
b) Apenas I e II são verdadeiras.
c) 180W
59. (PUC-Minas) O rendimento de uma máquina térmica é
a razão entre o trabalho realizado e o calor absorvido,
por ciclo.
P (Pa). 105
c) Apenas II e III são verdadeiras.
4
d) Apenas I e III são verdadeiras.
2
e) I, II e III são verdadeiras.
56. (AFA) Um motor térmico que funciona segundo o ciclo
de Carnot, absorve 400cal de uma fonte quente a 267oC
e devolve 220cal para uma fonte fria. A temperatura da
fonte fria, em oC, é:
V (m3)
0
0,1
0,2
Calcule o rendimento η de uma máquina térmica que
segue o ciclo descrito pelo diagrama seguinte, sabendo
que ela absorve 8,0 × 104J de energia térmica por ciclo.
a) 12
b) 24
c) 147
d) 297
57. (UFCE) O “ciclo diesel”, mostrado na figura abaixo,
representa o comportamento aproximado de um motor
a diesel. A substância de trabalho desse motor pode
ser considerado um gás ideal. O processo a → b é
uma compressão adiabática, o processo b → c é uma
expansão à pressão constante, o processo c → d é
uma expansão adiabática e o processo d → a é um
resfriamento a volume constante.
P
b
a) 3,0atm
b) 4,0atm
c) 7,0atm
d) 11atm
c
e) 14atm
d
a
EM_V_FIS_015
1. (MED-SM-RJ) Uma determinada amostra de um gás
ideal ocupa um volume de 12,0 , quando à pressão de
1,00atm e à temperatura de 27oC. Aumentando-se de
100oC a temperatura do gás e reduzindo-se seu volume para 4,0 , o valor aproximado de sua nova pressão
será de:
V
Com relação a esses processos, assinale a opção correta:
a) No processo a→ b a energia interna do sistema
não varia.
2. (UFF) Uma certa quantidade de gás perfeito evolui de
um estado I para um estado II e deste para um estado
III, de acordo com o diagrama pressão × volume representado. Sabendo que a temperatura no estado I é de
57oC, podemos afirmar que a temperatura no estado
III é de:
Esse material é parte integrante do Aulas Particulares on-line do IESDE BRASIL S/A,
mais informações www.aulasparticularesiesde.com.br
23
a) sextuplica.
P (atm )
4
b) reduz-se à sexta parte.
I
3
2
c) reduz-se à metade.
III
II
1
d) triplica.
V (litros)
2 4 6 8 10 12
e) reduz-se à terça parte.
a) 95K
b) 120K
c) 250K
d) 330K
e) 550K
3. (Unificado) Um gás ideal evolui de um estado A para
um estado B, de acordo com o gráfico representado
abaixo.
6. (Cesgranrio) Antes de sair em viagem, um automóvel tem
seus pneus calibrados em 24 (na unidade usualmente utilizada nos postos de gasolina), na temperatura ambiente
de 27oC. Com o decorrer da viagem, a temperatura dos
pneus aumenta e a sua pressão passa para 25, sem que
seu volume varie. Assim, nessa nova pressão, é correto
afirmar que a temperatura do ar no interior dos pneus
passou a valer, em ºC:
a) 39,5
b) 37,2
P (atm )
c) 32,5
B
1,8
1,0
d) 28,6
e) 28,1
A
v (g)
0
2,4
5,0
A temperatura no estado A vale 80K. Logo, sua
temperatura no estado B vale:
a) 120K
7.
(Unificado) Dois recipientes (I e II na figura abaixo),
de volumes respectivamente iguais a V e 2V, são interligados por um tubo de volume desprezível provido de
uma válvula S.
S
b) 180K
V
c) 240K
d) 300K
Recipiente I
e) 360K
4. (UFF) A pressão do ar dentro dos pneus é recomendada
pelo fabricante para situações em que a borracha está fria.
Quando o carro é posto em movimento, os pneus aquecem,
a pressão interna varia e o volume do pneu tem alteração
desprezível.
Considere o ar comprimido no pneu como um gás ideal
e sua pressão a 17oC igual a 1,7 × 105N/m2.
Depois de rodar por uma hora, a temperatura do pneu
chega a 37oC e a pressão do ar atinge o valor aproximado
de:
a) 7,8 × 104N/m2
b) 1,7 × 105N/m2
c) 1,8 × 105N/m2
d) 3,4 × 105N/m2
e) 3,7 × 105N/m2
24
2V
5. (MED-FESO-RJ) Sob pressão constante, ao triplicarse a temperatura de uma certa massa de gás, seu
volume:
Recipiente II
Inicialmente, com a válvula S fechada, o recipiente I contém
um gás perfeito à pressão P0 e o recipiente II está vazio. A
seguir, abre-se a válvula S. Sabendo-se que a temperatura
final do gás nos dois recipientes é igual a sua temperatura
inicial, pode-se afirmar que a pressão final do gás no
recipiente II será:
a) P0
b) 2P0
1
c) P0
2
d) 3P0
1
e) P0
3
8. (Unesp) O ar do ambiente a 27oC, entra em um secador
de cabelos (aquecedor de ar) e dele sai a 57oC, voltando
para o ambiente. Qual a razão entre o volume de certa
massa de ar quando sai do secador e o volume dessa
mesma massa quando entrou no secador? Suponha que
o ar se comporte como um gás ideal.
Esse material é parte integrante do Aulas Particulares on-line do IESDE BRASIL S/A,
mais informações www.aulasparticularesiesde.com.br
EM_V_FIS_015
0
9. (UFF) O êmbolo de figura pode se mover sem atrito e
sem deixar escapar o gás ideal contido no cilindro. Inicialmente a temperatura do gás é de 27ºC. Esquenta-se
o sistema lentamente até que a altura h aumente 50%
em relação a seu valor inicial. Qual a temperatura final
do gás?
GÁS
h
Qual a temperatura
final do gás?
No instante em que se inicia o colapso a temperatura no
interior da câmara é de 7,0ºC. Calcule nesse instante:
a) a pressão no interior da câmara.
b) a força a que cada parede da câmara estava submetida.
13. (Unificado) Dois recipientes de mesmo volume estão
ligados por um tubo de diâmetro pequeno provido de um
registro (inicialmente fechado). O recipiente (1) contém
4 moles de hidrogênio a 300K. O recipiente (2) contém
n moles do mesmo gás à temperatura T.
V
10. (Fuvest) Um recipiente indeformável, hermeticamente
fechado, contém 10 litros de um gás perfeito a 30ºC,
suportando uma pressão de 2 atmosferas. A temperatura
do gás é elevada, até atingir 60ºC.
a) esboce o gráfico pressão x temperatura da transformação descrita.
b) calcule a pressão final do gás.
11. (Unicamp) Calibra-se a pressão dos pneus de um carro
em trinta psi (libras-força/polegada2) usando nitrogênio
na temperatura ambiente (27oC).
Para simplificar os cálculos adote 1 polegada = 2,5cm;
1 libra força = 5N; R = 8,0J/mol.K.
a) Quanto vale essa pressão em N/m2.
b) Faça uma estimativa do volume do pneu e com a mesmo estime o número de mols de nitrogênio contido
no pneu.
c) Em um dia quente, a temperatura do pneu em movimento atinge 57oC. Qual é a variação percentual
da pressão no pneu.
12. (UFRJ) Um inventor, preocupado com economia de
energia, constrói uma câmara frigorífica que, uma vez
fechada a porta, não permite qualquer entrada ou saída
de ar. Em seu primeiro teste, a câmara é fechada e seu
sistema de refrigeração é ligado; após algum tempo de
funcionamento, para decepção do inventor, a câmara
frigorífica sofre um colapso, contraindo-se até ficar
bastante amassada, conforme ilustrado a seguir:
0,75m2
(1)
V
registro
(2)
Assinale, entre as opções oferecidas, aquela que
indica valores de n e T compatíveis com a observação
experimental seguinte: “ao abrir-se o registro, verificase um fluxo de gás do recipiente (1) em direção ao
recipiente (2)”.
n
T(K)
a) 2
600
b) 2
450
c) 3
500
d) 4
400
e) 6
250
14. (UFF) Um gás ideal estava confinado à mesma temperatura em dois recipientes, 1 e 2, ligados por uma válvula
inicialmente fechada. Os volumes dos recipientes 1 e 2 são
4 e 6 , respectivamente. A pressão inicial no recipiente
1 era de 4,8atm.
Abriu-se a válvula e os conteúdos dos recipientes atingiram
um estado final de equilíbrio à pressão de 2,4 atm e à
mesma temperatura inicial.
válvula
recipiente 1
recipiente 2
EM_V_FIS_015
A porcentagem do número total de mols de gás que
ocupava o recipiente 1 antes da abertura da válvula era:
a) 60%
Para entender o fenômeno, considere o ar no interior da
câmara frigorífica como um gás perfeito. Considere também
que, no instante em que a câmara é fechada, o ar tem
pressão igual à pressão atmosférica, de 1,0 × 105N/m2, e
temperatura igual a do ambiente, de 27ºC.
b) 80%
c) 50%
d) 40%
e) 20%
Esse material é parte integrante do Aulas Particulares on-line do IESDE BRASIL S/A,
mais informações www.aulasparticularesiesde.com.br
25
15. (UFRRJ) No gráfico estão representadas duas isotermas
e três transformações sucessivas: 1→2, 2→3, 3→4.
A sequência das transformações é, respectivamente:
P
e) V
18. (Unifor) Um recipiente metálico aberto está a uma
temperatura de 300K e contém certa massa de gás m.
Aquecendo-se o conjunto até 600K, à pressão constante, certa massa de gás escapa e o recipiente é lacrado.
Nessas condições, calcule a quantidade de gás que
permanece no recipiente:
2
V
0
a) isométrica, adiabática, isotérmica.
b) isotérmica, isométrica, isobárica.
19. (PUC-Rio) Em um recipiente de 8 de capacidade colocamos
12 de oxigênio a 27ºC e sob pressão de 2atm, com 6 de
hidrogênio a 57°C e sob pressão de 4atm. Calcular a pressão
da mistura sabendo que a temperatura final é 37ºC.
c) adiabática, isotérmica, isobárica.
d) isométrica, isotérmica, isobárica.
e) isobárica, isotérmica, isométrica.
16. (PUC-Rio) Uma certa massa gasosa m de um gás ideal
encontra-se em equilíbrio termodinâmico. Nessas condições, sua massa específica é µ seu volume é V, sua
temperatura T e sua pressão P. Em seguida, essa massa
m sofre uma transformação gasosa, onde sua densidade passa a ser µ’, a pressão P/6 e a temperatura T/3.
Supondo um novo equilíbrio termodinâmico, a massa
específica µ’ é de:
a) µ 6
b) µ 2
c) 2
d) 6
µ
e)
12
17. (UERJ) As figuras abaixo representam cinco recipientes
metálicos de volumes diferentes, em equilíbrio térmico
com o meio ambiente. Todos os recipientes contêm
oxigênio e são dotados de manômetros que informam
a pressão do gás contido neles.
0,80atm
20
30
I
II
III
1,20atm
IV
26
0,90atm
10
0,40atm
40
V
Sabendo-se que, nessas condições, o oxigênio se comporta
como um gás perfeito e tendo-se em conta os valores dos
volumes e das pressões indicados nas figuras, pode-se
concluir que o recipiente que contém mais moléculas de
oxigênio é a figura:
20. (Fuvest) Um cilindro metálico fechado com tampa contém 6,0mols de ar à pressão de 4atm e na temperatura
ambiente. Abre-se a tampa do cilindro. Depois de seu
conteúdo ter entrado em equilíbrio termodinâmico com
o ambiente, qual é o número de mols que permanecerão
no cilindro?
21. (Unicamp) Um balão meteorológico de cor escura, no
instante de seu lançamento contém 100mols de moléculas
do gás hélio (He). Após subir a uma altitude de 15km, a
pressão do gás se reduziu a 100mmHg e a temperatura,
devido à irradiação solar, aumentou para 77ºC.
Dados: constante dos gases ideais = R = 62 . mmHg.
K-1 . mol-1; massa molar do He = 4g/mol.
Nessas condições, calcule:
a) o volume do balão.
b) a densidade do He no interior do balão.
22. (EsFAO) Um sensor térmico experimental é constituído
por um recipiente contendo um gás perfeito e um êmbolo
que permite alterações do volume do gás.
70
60
50
40
30
20
10
0
x (mm)
4
8
12 16 20 24
hora do dia
O gráfico anterior representa os resultados de um
experimento que consistiu em variar, sob pressão
atmosférica constante, a temperatura do gás ao longo
de um dia, registrando-se a posição do êmbolo.
a) Indique o horário em que ocorre o registro de 50mm.
b) Calcule a posição correspondente à temperatura de
80oC, sabendo-se que a posição de 45mm é atingida
na temperatura de 30oC. Considere a aproximação
0oC = 270K.
Esse material é parte integrante do Aulas Particulares on-line do IESDE BRASIL S/A,
mais informações www.aulasparticularesiesde.com.br
EM_V_FIS_015
1
50
c) III
d) IV
3
1,20atm
b) II
posição êmbolo em mm
4
a) I
23. (ITA) Um tubo capilar de comprimento 5a é fechado
em ambas as extremidades. Ele contém ar seco, que
preenche o espaço no tubo não ocupado por uma
coluna de mercúrio de densidade ρ e comprimento a.
Quando o tubo está na posição horizontal, as colunas de
ar seco medem 2a cada. Levando-se lentamente o tubo
à posição vertical, as colunas de ar têm comprimento a e
3a. Nessas condições, a pressão no tubo capilar quando
em posição horizontal é:
2a
Hg
ar
2a
ar
a
a)
3a
ar
a
a
I. A energia interna de um gás ideal depende só da
pressão.
II. Quando um gás passa de um estado 1 para outro
2, o calor trocado é o mesmo qualquer que seja o
processo.
III. Quando um gás passa de um estado 1 para o estado 2, a variação da energia interna é a mesma
qualquer que seja o processo.
IV. Um gás submetido a um processo quase-estático
não realiza trabalho.
Hg
ar
V. O calor específico de uma substância não depende
do processo como ela é aquecida.
VI. Quando um gás ideal recebe calor e não há variação de volume, a variação da energia interna é igual
ao calor recebido.
3gra
4
VII.Numa expansão isotérmica de um gás ideal, o trabalho realizado é sempre menor do que o calor absorvido.
b) 2gra
5
As duas corretas são:
a) II e III
2gra
3
4gra
d) 3 c) b) III e IV
4gra
e)
5
24. (PUCRS) Um sistema formado por um gás ideal sofre
uma transformação com as seguintes características:
∆Q = ∆U e W = 0. Onde W é o trabalho realizado, ∆U
é uma variação positiva (aumento) da energia interna e
∆Q é o valor fornecido ou absorvido pelo sistema. Esses
dados permitem concluir que no processo houve uma
transformação:
a) adiabática.
c) III e V
d) I e VII
e) III e VI
27. (FEI-SP) Um gás ideal sofre uma transformação isotérmica recebendo do meio ambiente 3 000J de calor. Sendo
n = 4 o número de mols do gás, podemos afirmar que a
variação de sua energia interna e o trabalho realizado na
transformação valem, em Joules, respectivamente:
a) 0 e 3 000
b) isobárica.
b) –2 000 e 0
c) isométrica.
c) 2 000 e –3 000
d) isotérmica.
d) 4 000 e 2 000
e) adiabática e isotérmica.
e) –3 500 e 800
25. (Cefet-RJ) Em um gás ideal, para uma expansão isotérmica, é correto afirmar que:
a) a pressão irá aumentar e a energia interna também.
b) a pressão irá aumentar e a energia interna permanecerá constante.
EM_V_FIS_015
26. (ITA) Das afirmações abaixo:
28. (UFF) 10 litros de gás à baixa pressão, contidos em um
recipiente, são aquecidos recebendo 1,0 × 102cal sem variar
significativamente o seu volume. Os valores aproximados
do trabalho (T) realizado no processo e da correspondente variação de energia interna (∆U) do gás são, em cal,
respectivamente:
c) a pressão permanecerá constante e a energia interna irá aumentar.
a) 0;0
d) a pressão irá diminuir e a energia interna permanecerá constante.
c) 1,0 × 1012 ; 0
e) a pressão irá diminuir e a energia interna irá aumentar.
e) 0,5 × 102; 0,5 × 102
b) 0; 1,0 × 102
d) 1,0 × 102; 1,0 × 102
Esse material é parte integrante do Aulas Particulares on-line do IESDE BRASIL S/A,
mais informações www.aulasparticularesiesde.com.br
27
29. (UFCE) Um recipiente fechado, contendo um gás perfeito, está inicialmente à temperatura T = 0oC. A seguir
o recipiente é aquecido até que a energia interna desse
gás duplique seu valor. A temperatura final do gás é:
a) 546K
peso do êmbolo mais o peso da coluna de ar acima dele
é de 400N. Uma quantidade de 28J de calor é, então,
transferida lentamente para o gás. Nesse processo,
o êmbolo se eleva de 0,02m e a temperatura do gás
aumenta de 20oC.
400N
b) 273K
400N
c) 0K
0,02 m
d) 273ºC
e) 00C
30. (Unirio) Um gás ideal encontra-se dentro de uma caixa
cúbica hermeticamente fechada. Ela é colocada sob a
ação de uma fonte térmica que lhe fornece, uniformemente, 400J/s.
Com isso, ela sofre uma dilatação térmica uniforme, de tal
forma que cada aresta aumenta o seu tamanho inicial em
10%. O tempo necessário para que ocorra essa dilatação
é de 1,0min, quando então a fonte térmica é afastada e
a caixa deixa de se dilatar. Considere que durante todo
o processo de dilatação da caixa a energia interna do
gás não varia. Determine:
a) o trabalho realizado pelo gás durante o período em
que ocorreu a dilatação térmica.
b) a pressão final do gás, em atm, sabendo que sua
pressão inicial, antes do aquecimento, é de 1,0atm.
31. (UERJ) Um cilindro de área de seção reta uniforme igual
a 0,10m2, dotado de um êmbolo que pode se mover sem
atrito, contém um gás ideal em equilíbrio. O êmbolo se
encontra a uma altura H = 0,50m acima da base do
cilindro, como mostra a figura.
H
Nessas condições, determine:
a) o trabalho realizado pelo gás.
b) o calor específico do gás no processo, sabendo
que sua massa é 1,4g.
33. (Fuvest) A figura mostra o corte transversal de um cilindro de eixo vertical com base de área igual a 500cm2,
vedado em sua parte superior por um êmbolo de massa
m que pode deslizar sem atrito.
m
gás
h
O cilindro contém 0,50mol de um gás que se comporta
como ideal. O sistema está em equilíbrio a uma
temperatura de 300K e a altura h, indicada na figura,
vale 20cm. Adote para a constante dos gases o valor R
= 8,0J/mol . K, para a aceleração da gravidade o valor
10m/s2 e para a pressão atmosférica local o valor 1,00×
105N/m2. Determine:
a) A massa do êmbolo em kg.
b) O trabalho W realizado pelo gás quando sua temperatura é elevada lentamente até 420K.
b) a pressão do gás no interior do cilindro.
32. (Unesp) Certa quantidade de um gás é mantida sob
pressão constante dentro de um cilindro com o auxílio
de um êmbolo pesado que pode deslizar livremente. O
28
34. (Cefet-RJ) 50,0 litros de um gás ideal a 27,0oC e sujeito
à pressão atmosférica normal, são colocados no interior
de um recipiente cilíndrico, dotado de êmbolo móvel,
de massa desprezível, que pode deslizar sem atrito.
A capacidade térmica do recipiente e do êmbolo são
desprezadas. O recipiente recebe calor de uma fonte
térmica de potência constante, indicada pelo gráfico
abaixo. Todo o calor fornecido pela fonte é absorvido
pelo gás. Após certo intervalo de tempo, observa-se que
o gás sofreu uma variação de volume correspondente a
20% de seu volume inicial, à pressão constante.
(Dados: 1,0atm = 1,0 × 105N/m2; 1,0cal = 4,2J)
Esse material é parte integrante do Aulas Particulares on-line do IESDE BRASIL S/A,
mais informações www.aulasparticularesiesde.com.br
EM_V_FIS_015
O gás sofre uma compressão isobárica, sendo realizado
sobre ele um trabalho de 1,0 × 103J. Em consequência,
o gás cede ao meio externo uma quantidade de calor
correspondente a 1,5 × 103J. No final do processo, o
sistema entra em equilíbrio quando o êmbolo atinge uma
altura de 0,40m acima da base do cilindro.
Calcule:
a) a variação da energia interna sofrida pelo gás.
Q (kcal)
60
t (h)
1,0
36. (UFF) O gráfico representa a transformação de um gás
ideal que passa do estado I para o estado II e, depois,
do estado II para o estado III.
Para que o gás passe do estado I para o II, é necessário
que lhe forneçam 100kJ de calor; para que passe do
estado II para o III, que lhe retirem 50kJ de calor.
V (m 3 )
Pede-se:
a) a temperatura final do gás em oC;
III
b) a potência da fonte em watts;
c) a quantidade de calor em joules, absorvida pelo gás,
sabendo-se que o recipiente ficou em contato com a
fonte térmica durante 2,5 minutos;
d) o trabalho que o gás realiza, em joules, nesse intervalo de tempo;
e) a variação da energia interna sofrida pelo gás nesse
intervalo de tempo, em joules.
35. (UFF) A figura ilustra a secção reta de um recipiente
isolante térmico cilíndrico, cujo volume é regulado por
um pistão que pode deslizar sem atrito. O pistão está
preso à mola de constante elástica k = 1,0 × 104N/m, que
se encontra relaxada quando o pistão está encostado
no fundo do recipiente.
�x
II
12
I
10
T (K)
100
120
Sabendo-se que a pressão do gás no estado I é de 100
kPa, pode-se afirmar que a variação da energia interna
do gás, ao passar do estado I para o III, é igual a:
a) zero
b) –200kJ
c) –50Kj
d) –140kJ
e) –150kJ
37. (UEL) O gráfico representa a pressão p, em função do
volume V, para um gás perfeito contido num cilindro
fechado por um pistão móvel. O trabalho realizado pelo
gás entre os pontos A e B, em joules, é de:
P (Pa)
R
6,10
6,0V
pistão
Certa quantidade de um gás ideal é colocada no
recipiente e, em equilíbrio térmico à temperatura
T = 27oC, a mola comprime-se de ∆x = 0,50m. (Dado:
constante universal dos gases R = 8,31J/mol.K)
a) Calcule o número de mols do gás no recipiente.
b) O gás é aquecido durante 10 minutos por meio de
um resistor com R = 20Ω, ligado a uma fonte de
tensão de 6,0V. Calcule a quantidade de calor fornecida ao gás.
Durante o aquecimento, o gás se expande quase
estaticamente e, ao final, no equilíbrio térmico, o pistão
encontra-se em uma nova posição onde a mola está
comprimida de ∆x1 = 0,55m. Tendo em vista essa nova
situação, calcule:
c) a temperatura do gás.
d) o trabalho mecânico realizado pelo gás na expansão de ∆x para ∆x1.
EM_V_FIS_015
B
4
e) a variação da energia interna do gás na expansão,
considerando desprezível a capacidade térmica do
sistema (recipiente e seus componentes).
4,104
0
A
V (m 3 )
2,10-3
6,10-3
a) 400
b) 200
c) 60
d) 40
e) 20
38. (Unirio) Um gás sofre a transformação cíclica ABCA,
indicada no gráfico a seguir.
P (N/m 2 )
B
600
200
C
A
1,0
V (m3)
5,0
A variação da energia interna e o trabalho realizado pelo
gás valem, respectivamente:
a) ∆U = 0J e W = 0J
b) ∆U = 0J e W = 8 × 102J
Esse material é parte integrante do Aulas Particulares on-line do IESDE BRASIL S/A,
mais informações www.aulasparticularesiesde.com.br
29
c) ∆U = 0,5 × 102J e W = 1,5 × 103J
d) ∆U = 8,0 × 102J e W = 0J
e) ∆U = 8,5 × 102J e W = 8,0 × 102J
39. (PUC-Rio) O diagrama abaixo mostra a evolução de um
gás ideal sob pressão constante de 20N/m2. O gás está
inicialmente no estado A e evolui para o estado B.
V(m3)
30
25
20
15
10
5
A
50
B
10
T (k)
100
42. (UFSC) O trabalho realizado quando um gás ideal se
expande do estado A até o estado B é de 50J, conforme a figura abaixo. Na transformação completa, isto é,
para o gás ir do estado A até o estado C, foi fornecida
uma quantidade total de calor igual a 160J. Qual é a
variação da energia interna do gás para a transformação
completa?
P (Pa)
A
B
3
V (M )
0 1 2 3 4 5 6 7 8 9 10
700
Durante esse processo, o gás cede 1 100J de calor para
o ambiente. Determine o trabalho realizado sobre o gás
(W) e sua variação de energia interna (∆U).
a) W = 18 000J; ∆U = 19 100J
43. (Unirio) Um gás, inicialmente a 0oC, sofre a transformação A → B → C representada no diagrama p × V da
figura abaixo.
b) W = 18 000J; ∆U = 16 900J
p (atm)
A
c) W = –800J; ∆U = –300J
d) W = 800J; ∆U = 1 900J
1,0
e) W = 800J; ∆U = 300J
5
P (10 Pa)
30
20
10
3
V (m )
1
2 3 4
5 6
7 8
a) 6 × 105J
b) 9 × 105J
c) 3 × 106J
d) 9 × 106J
V( )
Sabendo-se que a transformação gasosa entre os
estados A e B é isotérmica e entre B e C é isométrica,
determine:
a) A variação da energia interna na transformação isotérmica.
44. (UFRJ) Um gás ideal, inicialmente em um estado de
equilíbrio termodinâmico (ponto 1 da figura) a uma
temperatura T, sofre uma expansão isobárica (1→ 2),
seguida de uma transformação isométrica (2 → 3),
até atingir o estado de equilíbrio (ponto 3 da figura) à
mesma temperatura inicial T, como ilustra o diagrama
PxV a seguir.
e) 6 × 106J
P (105N/m2)
41. (Unirio) O gráfico abaixo mostra uma transformação
ABC sofrida por certa massa de gás ideal (ou perfeito),
partindo da temperatura inicial 300K. determine:
P (N/m )
1
2
3
isoterma
V (10-3m3)
10,0
a) Durante a evolução 1 → 2 → 3, o gás cedeu ou
recebeu calor?
A
C
5,0
V (cm )
3
a) a temperatura do gás no estado C.
b) o trabalho realizado pelo gás na transformação AB.
45. (UFOP) O diagrama a seguir mostra uma transformação
na qual 100mols de moléculas de gás ideal monoatômico
recebem do meio exterior uma quantidade de calor igual
a 18 . 105J. Determine: ( R = 8,31J/mol K)
Esse material é parte integrante do Aulas Particulares on-line do IESDE BRASIL S/A,
mais informações www.aulasparticularesiesde.com.br
EM_V_FIS_015
b) Calcule essa quantidade de calor.
B
1,0 3,0
2,0
5,0
2
30
B
b) A pressão do gás, em atm, quando ele se encontra
no estado C, considerando que, nesse estado, o
gás está à temperatura de 273oC.
40
20
C
0
40. (ITA) O gráfico representa um ciclo de um sistema
termodinâmico hipotético, num diagrama p × V. O
trabalho produzido por esse gás, nesse ciclo, é de
aproximadamente:
80
C
2
p (N/m )
2
5
6,10
5
3,10
1
3
V (m )
0
1
2
a) o trabalho realizado pelo gás;
b) a variação de energia interna do gás;
exemplo — representa um problema para as pessoas,
pois sua utilização como água potável só é possível
após passar por um processo de dessalinização. Um
dispositivo para esse fim (e que utiliza radiação solar) é
o destilador solar. Ele é composto basicamente por um
reservatório d’água cujo fundo é pintado de preto fosco,
uma cobertura de placas de vidro transparente e calhas
laterais para coletar a água condensada nas placas de
vidro, conforme ilustrado na figura a seguir.
c) a temperatura do gás no estado 1.
46. (UFRJ) Um sistema termodinâmico realiza o ciclo a →
b → c → d → a, conforme é mostrado no diagrama
pressão × volume da figura.
2
12 o
P (N/m )
b
a
4po
3po
po
c
d
Vo
3
V (m )
11 Vo
a) Calcule o trabalho realizado pelo sistema no ciclo
a → b → c → d → a.
b) Calcule o saldo final de calor recebido pelo sistema
no ciclo a → b → c → d → a.
47. (UFRJ) Um mol de um gás ideal encontra-se em equilíbrio termodinâmico numa temperatura T0. Cede-se a
esse gás uma certa quantidade de calor Q.
Se o aquecimento for a volume constante (figura 1),
ele atingirá uma temperatura T1. Se o aquecimento
for à pressão constante (figura 2), ele atingirá uma
temperatura T2.
P
b) o processo de condensação do vapor de água ocorre nas placas de vidro que estão à mesma temperatura do vapor.
c) a condução térmica não atua no processo de dessalinização da água.
d) a entropia do vapor de água diminui quando o vapor se condensa nas placas de vidro.
50. (UFF) O diagrama pressão (P) × volume (V), a seguir,
representa uma transformação quase estática e cíclica
de um gás ideal.
P
P1
T1
To
po
po
To
T2
Vo
Vo
Compare T1 e T2 e verifique se T1 > T2 , T1 = T2 ou T1 < T2.
Justifique sua resposta.
48. (AFA) Certa máquina térmica opera entre as temperaturas de 27ºC e 477ºC, em um ciclo que absorve 5kJ da
fonte quente e libera 2kJ para a fonte fria. Isso posto, é
possível afirmar que:
a) o rendimento da máquina é 40%.
b) o rendimento da máquina é 94%.
c) a máquina obedece a um ciclo reversível.
d) a máquina obedece a um ciclo irreversível.
49. (UFRN) A água salobra existente em muitos locais — em
algumas cidades no interior do Rio Grande do Norte, por
1
2 ISOTERMA
P2
P4
P3
V
EM_V_FIS_015
Com base no exposto acima, é correto afirmar:
a) a energia da radiação solar é utilizada para condensação do vapor de água.
4
V1 V4
3 ISOTERMA
V2 V3
Considere o diagrama e assinale a opção correta.
a) A maior temperatura atingida pelo gás no ciclo
ocorre na passagem do estado 3 para o estado 4.
b) O trabalho realizado pelo gás no ciclo é nulo.
c) A transformação que leva o gás do estado 2 para o
estado 3 é isotérmica.
d) A variação da energia interna no ciclo é nula.
e) O gás sofre uma expansão adiabática ao passar do
estado 1 para o estado 2.
51. (Fuvest) Um sistema formado por um gás ideal sofre
uma transformação com as seguintes características:
W = –∆U e Q = 0, onde W é a trabalho realizado, ∆U é
Esse material é parte integrante do Aulas Particulares on-line do IESDE BRASIL S/A,
mais informações www.aulasparticularesiesde.com.br
31
uma radiação positiva (aumento) de energia interna e
Q é o calor fornecido ou absorvido pelo sistema. Esses
dados permitem concluir que a transformação foi uma:
a) compressão adiabática.
b) compressão isotérmica.
c) expansão adiabática.
d) expansão isotérmica.
e) expansão isobárica.
52. (ITA) Um recipiente de volume ajustável contém n mols
de um gás ideal. Inicialmente o gás está no estado
A, ocupando o volume V à pressão p. Em seguida , o
gás é submetido à transformação indicada na figura.
Calcular o calor absorvido pelo gás na transformação
cíclica ABCA.
a) Indique se o módulo QA do calor absorvido na transformação BC é maior, igual ou menor que o módulo
QC do calor cedido na transformação DA. Justifique
sua resposta.
b) Calcule a variação da energia interna nesse ciclo.
55. (Unicamp) Um mol de gás ideal sofre a transformação
A → B → C iniciada no diagrama pressão x volume da
figura.
P (atm)
A
3,0
B
C
V (L)
isoterma
0
8,0
10,0
a) Qual é a temperatura do gás no estado A?
a) 0
npv
b)
2
–npv
c)
2
pv
d)
2
–pv
e)
2
53. (ITA) Um centímetro cúbico de água passa a ocupar
1 671cm3 quando evapora à pressão de 1,0atm. O calor
de vaporização a essa pressão é de 539cal/g. O valor
que mais se aproxima do aumento de energia interna
da água é:
a) 498cal
c) Qual é a temperatura do gás no estado C?
Dado: R (constante dos gases)=0,082atm /mol
= 8,3J/mol K.
56. (UFRJ) A figura representa, num gráfico pressão x
volume, um ciclo de um gás ideal.
p
0,75
0,50
105N
m2
A
B
D
C
v (10-2m3)
2
b) 2 000cal
6
a) Calcule o trabalho realizado pelo gás durante esse
ciclo.
c) 498J
e) 2 424J
54. (UFRJ) Um gás ideal realiza o ciclo termodinâmico constituído por duas isotermas, AB e CD, e duas isóbaras,
BC e DA, ilustradas na figura abaixo. As temperaturas
correspondentes às isotermas AB e CD valem 300K e
500K, respectivamente.
57. (Enem) Nos últimos anos, o gás natural (GNV: gás natural
veicular) vem sendo utilizado pela frota de veículos nacional, por ser viável economicamente e menos agressivo do
ponto de vista ambiental.
O quadro compara algumas características do gás
natural e da gasolina em condições ambiente.
Esse material é parte integrante do Aulas Particulares on-line do IESDE BRASIL S/A,
mais informações www.aulasparticularesiesde.com.br
EM_V_FIS_015
b) Calcule a razão entre a mais alta e a mais baixa temperatura do gás (em Kelvin) durante esse ciclo.
d) 2 082J
32
b) Qual é o trabalho realizado pelo gás na expansão
A→ B?
Massa específica
(kg/m3)
Poder calorífico
(kJ/kg)
GNV
0,8
50 200
Gasolina
738
46 900
Apesar das vantagens no uso de GNV, sua utilização
implica algumas adaptações técnicas, pois, em condições
ambiente, o volume de combustível necessário, em
relação ao de gasolina, para produzir a mesma energia,
seria:
a) muito maior, o que requer um motor muito mais potente.
b) muito maior, o que requer que ele seja armazenado
à alta pressão.
c) igual, mas sua potência será muito menor.
d) muito menor, o que o torna o veículo menos eficiente.
e) muito menor, o que facilita sua dispersão para a atmosfera.
II. Manter as paredes do congelador com camada bem
espessa de gelo, para que o aumento da massa de
gelo aumente a troca de calor no congelador.
III. Limpar o radiador (“grade” na parte de trás) periodicamente, para que a gordura e a poeira que nele
se depositam não reduzam a transferência de calor
para o ambiente.
Para uma geladeira tradicional é correto indicar, apenas:
a) a operação I.
b) a operação II.
c) as operações I e II.
d) as operações I e III.
e) as operações II e III.
60. (AFA) Uma máquina térmica funciona de acordo com
o ciclo dado pela figura abaixo. Essa máquina foi construída usando 2mols de um gás monoatômico, e no
decorrer de cada ciclo não há entrada nem saída de
gás no reservatório que o contém.
58. (UFF) Considere 4mols de um gás ideal, inicialmente
a 2oC de temperatura e 8,20atm de pressão, que se
submete ao seguinte ciclo de transformações:
p (105N/m2)
2º. aquecimento isobárico até a temperatura de 57oC.
2
3º. despressurização isovolumétrica até a pressão de
8,20 atm.
0
4º. resfriamento isobárico até retornar às condições iniciais.
Represente esse ciclo em um gráfico p(atm) versus
V(litros), indicando os valores de p,V e T ao final de cada
uma das transformações dadas acima.
a) Calcule o trabalho, em joules, realizado pelo gás no
ciclo.
b) Calcule o calor, em joules, absorvido pelo gás no ciclo.
EM_V_FIS_015
c) Calcule a potência, em watts, de um motor que realiza 10 desses ciclos por segundo.
Dados: R(constante de gases) = 0,082atm. /mol.K;
1atm = 105Pa; 0oC = 273K.
59. (Enem) A refrigeração e o congelamento de alimentos
são responsáveis por uma parte significativa do consumo
de energia elétrica numa residência típica.
Para diminuir as perdas térmicas de uma geladeira,
podem ser tomados alguns cuidados operacionais:
I. Distribuir os alimentos nas prateleiras deixando espaços vazios entre eles, para que ocorra a circulação do ar frio para baixo e do quente para cima.
B
4
1º. compressão isotérmica, cedendo 860J de calor, até
o volume de 10 .
A
2,4
C
D
3,2
V (10-2m3)
4,8
O máximo rendimento e o trabalho realizado por essa
máquina valem, respectivamente:
a) 13% e 8 × 102J
b) 75% e 8 × 102J
c) 13% e 4 × 103J
d) 75% e 4 × 103J
61. (ITA) Uma máquina térmica reversível opera entre dois
reservatórios térmicos de temperaturas 1000C e 1270C,
respectivamente, gerando gases aquecidos para acionar uma turbina. A eficiência dessa máquina é melhor
representada por:
a) 68%
b) 6,8%
c) 0,68%
d) 21%
e) 2,1%
62. (PUC-Rio) Uma máquina de Carnot é operada entre
duas fontes, cujas temperaturas são, respectivamente,
Esse material é parte integrante do Aulas Particulares on-line do IESDE BRASIL S/A,
mais informações www.aulasparticularesiesde.com.br
33
100oC e 0oC. Admitindo-se que a máquina recebe da
fonte quente uma quantidade de calor igual à 1 000cal
por ciclo, pede-se:
a) o rendimento térmico da máquina;
b) o trabalho realizado pela máquina em cada ciclo,
em J;
c) a quantidade de calor rejeitada para uma fonte fria.
63. (Unirio) Uma máquina térmica recebe 3,6 × 104cal e
realiza um trabalho útil de 3,0 × 104J. Considerando
que o trabalho da máquina é obtido isobaricamente a
uma pressão de 2atm, num pistão que contém um gás,
determine:
a) o trabalho realizado pelo gás durante a compressão
da mola;
b) a variação da energia interna do gás, em joules.
a) A variação de volume sofrida pelo gás dentro do
pistão.
b) a variação de energia interna do gás.
64. (Unicamp) Um mol de gás ideal realiza um processo
cíclico A → B → C → A, representado no diagrama
V × T.
V (1)
3
1
C
B
A
T (k)
0
300
Sabendo que R = 0,082atm . L/mol.K = 8,31J/mol.K.
a) represente o mesmo processo no diagrama P × V.
b) calcule o trabalho realizado durante a expansão do
gás.
65. (ITA) Um inventor afirma ter projetado um carro que
utiliza energia solar para se movimentar. Segundo ele,
vencendo uma força de resistência de 2 100N, o carro
pode manter uma velocidade constante v = 72km/h. Sabendo que a quantidade de calor que atinge a superfície
da Terra é da ordem de 1cal/min, em cada cm2, normal à
direção de incidência, e que a área coletora de energia
do carro é de 10m2 , calcule o rendimento desse carro
quando desenvolver a velocidade v.
34
EM_V_FIS_015
66. (Cefet-RJ) No mecanismo abaixo, inicialmente a mola
encontra-se relaxada, encontrando-se a parte C preenchida por um gás ideal. Em determinado momento, o
gás é aquecido, recebendo 400cal de uma fonte, o que
provoca um deslocamento de 8cm do êmbolo. Despreze
os atritos e as massas da mola e do êmbolo. (Considere
k = 500N/cm e 1cal = 4,0J e despreze as perdas)
Esse material é parte integrante do Aulas Particulares on-line do IESDE BRASIL S/A,
mais informações www.aulasparticularesiesde.com.br
16. E
17. A
1. C
3. D
19. T = 354,9K
n
20. 2 = 3
n1
4
4. B
21. A
5. E
22. C
6. B
23. D
7.
B
24. C
8. D
25. B
9. p = 2,04atm
26. E
10. p = 2,72atm
27. B
11. A
28. E
2. D
12. A
13. C
EM_V_FIS_015
18. C
14. E
15. D
29.
a) G = 200J
b) T’ = 300K
Esse material é parte integrante do Aulas Particulares on-line do IESDE BRASIL S/A,
mais informações www.aulasparticularesiesde.com.br
35
30. Fazendo os gráficos:
56. B
57. C
58. B
59. 25%
Como o trabalho realizado é igual a área do gráfico,
W12 > W13 .
31. C
1. B
2. E
32. D
3. D
33. A
4. C
34. B
5. D
35. D
6. A
36. C
7.
37. B
8.
38. τ = 80J
39. τ1 > τ2 ⇒ Q1 > Q2
40.
V
V0
= 1,1
9. T = 450K = 177oC
10.
P
a) τAD = 1J
a)
b) ponto D
2.2
41. A
2
42. A
0
43. D
303
333
T (k)
b) p = 2,2atm.
44. E
11.
45. D
a) A pressão manométrica vale Pmm = 2,4 . 105 n/m2
46. A
b) Considerando um pneu de raio externo 25cm e raio
interno 15cm, sendo a largura 15cm temos um volume de:
47. D
48. C
c) V = 24 . 10–3m3
49. τBA = –14kJ
A pressaõ total é PTot = 3,4 . 105
Logo: n = 3,14mols
P2
= 1,1
P0
50.
a) τABC = 1 350J
b) Q = 4,5 . 106J
52. A
53. B
12.
a) p = 9,3 × 104Pa
b) F = 5 250N
54. C
13. B
55. D
14. B
Esse material é parte integrante do Aulas Particulares on-line do IESDE BRASIL S/A,
mais informações www.aulasparticularesiesde.com.br
EM_V_FIS_015
51. C
36
E
15. D
35.
16. B
a) n = 1,0028mol
17. C
b) Q = 1 080J
18. m1 =
c) T = 363K
m
2
d) τ = 262,5J
19. Pm = 5,92atm
e) Q = 817,5J
20. n = 1,5mols
36. E
21.
37. B
a) V = 21 700L
38. B
b) µ = 0,018g
39. C
22.
40. E
a) t = 20:00h
41.
b) h2 = 52,2mm
a) T = 375K
23. A
b) 100J
24. C
42. ∆U = 20J
25. D
43.
26. E
a) ∆U = 0J
27. A
b) pC = 2,0atm
28. B
44.
29. A
a) Na evolução ∆T = 0 ⇒ ∆U = 0. A variação de volume é positiva, portanto, τ>0: Então Q > O, logo,
o gás recebeu calor.
30.
a) τ = 24 000J
b) τ = 1 000J
b) p = 0,75atm
45.
31.
a) τ = 4,5 . 105J
a) ∆U = − 500J
b) ∆U = 13,5 × 105J
b) p =1,0 × 105N/m2
c) T1 = 361K
32.
a) τ = 8J
103J
b) cp =
kg.K
46.
a) τ = 50P0 V0
33.
b) Q = 50P0 V0
a) m = 100kg
47. Temos ∆U = Q − τ, a volume constante o trabalho é
nulo, logo: ∆U1 = Q.
b) τ = 480J
34.
a) T = 360K = 87°C
EM_V_FIS_015
b) Pot = 70w
No segundo caso ∆U2 = Q − τ e ∆U1 > ∆U2 ⇒
∆T1 > ∆T2 e T1 > T2 .
48. C
c) 1,05 × 104J
49. D
d) τ = 1,0 × 103J
50. D
e) ∆U = 9,5 × 103J
51. A
Esse material é parte integrante do Aulas Particulares on-line do IESDE BRASIL S/A,
mais informações www.aulasparticularesiesde.com.br
37
52. E
65. n = 600% (projeto inviável)
66.
53. D
a) τ =160J
54.
a) |QA| = |QC|
b) Q = 1 440J
b) ∆U = 0
55.
a) T = 292,7K
b) τ = 6 × 102J
c) TA = TC = 292,7K
56.
a) τ = 1 . 103J
b)
TB
= 4,5
TB
57. B
58.
a) τABCDA = 124J
b) Q = τ = 124J
c) P = 1 240W
59. D
60. D
61. B
62.
a) n = 26,8%
b) τ = 1 120,24J
c) Q1 = 732cal
63.
a) ∆V = 0,15m3
b) ∆U = 121 200J
64.
EM_V_FIS_015
a)
b) τ = 4 920J
38
Esse material é parte integrante do Aulas Particulares on-line do IESDE BRASIL S/A,
mais informações www.aulasparticularesiesde.com.br
EM_V_FIS_015
Esse material é parte integrante do Aulas Particulares on-line do IESDE BRASIL S/A,
mais informações www.aulasparticularesiesde.com.br
39
EM_V_FIS_015
40
Esse material é parte integrante do Aulas Particulares on-line do IESDE BRASIL S/A,
mais informações www.aulasparticularesiesde.com.br