Mecânica Muscular - Departamento de Física da Universidade de

Universidade de Coimbra
Faculdade de Ciências e Tecnologias
Departamento de Física
*Modelos dos Processos Fisiológicos no Homem*
Mecânica Muscular
Realizado por:
Ana Saiote [email protected]
Áurea Matias
Gilberto Almeida
Catarina Pereira
Resumo
™ Apresentação do tecido muscular do ponto de vista fisiológico:
→Tipos de músculo/ Características gerais
→ Músculo Esquelético: estrutura e funcionamento
™ Análise quantitativa da contracção muscular – comportamento
Microscópico:
→ Variação da densidade populacional ao longo do tempo.
→ Variação da força de contracção ao longo do tempo
→ Relação entre a densidade populacional e o deslocamento dos
filamentos
™ Simulação em Matlab de uma contracção
™ Análise quantitativa da contracção muscular – comportamento
macroscópico
Balanço humano de um pêndulo invertido: Será o tamanho da
oscilação controlada pela impedância do tornozelo? – exemplo de
aplicação
™Simulação em Simulink
™ Discussão / Conclusões
Definição de Músculo
O músculo é um tecido formado por um conjunto de
células especializadas capazes, graças à sua contracção
e relaxação, de criar movimento tanto do próprio corpo em
relação ao ambiente que o cerca, como dos órgãos entre si
e dentro dele.
Características gerais do
funcionamento do músculo
a) Contractilidade
b) Excitabilidade
c) Expansibilidade
d) Elasticidade
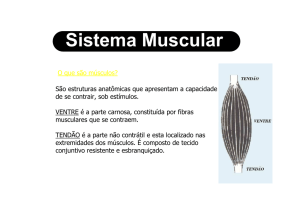
Músculo Esquelético: Estrutura
Os músculos esqueléticos compõem-se de
fibras musculares esqueléticas associadas a
pequenas quantidades de tecido conjuntivo, vasos
sanguíneos e nervos.
¾ Cada fibra muscular é envolvida por uma lâmina
externa – Sarcolema
¾ O endomísio (rede de tecido conjuntivo com muitas
fibras reticulares) envolve cada fibra muscular por fora
da lâmina externa
¾O perimísio (outra camada de tecido conjuntivo)
envolve cada feixe de fibras musculares com o seu
endomísio
¾ O epimísio, tecido conjuntivo mais denso, rodeia os
feixes de fibras agrupados, cobrindo toda a superfície
muscular
Fibras Musculares
Cada fibra muscular contém miofibrilhas. Estas
compõem-se de duas espécies de filamentos proteicos:
* miofilamentos de actina, ou miofilamentos finos
* miofilamentos de miosina, ou miofilamentos
grossos.
Estes miofilamentos de actina e miosina
organizam-se em unidades altamente ordenadas,
denominadas sarcómeros.
• Cada sarcómero estende-se de uma linha Z para a
linha Z imediata
→ Linha Z: rede filamentosa de proteínas que
faz a ligação dos miofilamentos de actina.
• O sarcómero está organizado em bandas:
* Banda I / isotrópica (banda clara)
* Banda A / anisotrópica (banda escura)
→ Banda H (centro da banda A)
→ Linha M – miofilamentos de proteínas
que fazem a ligação dos miofilamentos
de miosina
Etapas no processo de contracção muscular:
1. Excitação da fibra muscular esquelética,
envolvendo o desencadear do potencial de acção
e a sua propagação
2. Acoplamento excitação/ contracção
3. Ciclo das pontes cruzadas: ligação,
deslizamento, separação
4. Relaxamento muscular
Ciclo das pontes cruzadas
• Durante a contracção muscular, formam-se pontes
entre as moléculas de actina e as cabeças das
moléculas de miosina
• O movimento voluntário das pontes faz com que os
miofilamentos de actina em cada extremidade do
sarcómero deslizem para além dos miofilamentos de
miosina no sentido da zona H - Contracção
• Consequentemente, as bandas I encurtam mas as
bandas A mantêm-se.
A zona H estreita-se ou chega a desaparecer
quando os miofilamentos de actina se juntam no
centro do sarcómero – Contracção total
Posteriormente, há um Relaxamento,
no qual as pontes se libertam, permitindo
que os sarcómeros se estendam
Considerações prévias:
1. Uma ponte está ligada na configuração de equilíbrio, quando não exerce
força no filamento fino
2. x é a deslocação da configuração de equilíbrio; p(x) representa a força no
filamento fino quando o deslocamento da ponte ligada é x
x2
x <x<x
∫ u( x)dx
3. Diferentes pontes têm diferentes valores de x. Define-se a função densidade
de população, ∫ u ( x)dx que representa a fracção de pontes ligadas com um
deslocamento x tal que x < x < x
1
2
x1
x2
x1
1
2
4. A força total exercida pelo músculo é a soma das forças exercidas pelas
diversas pontes
5. A população de pontes está num estado estacionário
x2
∫ u( x)dx
6. Todas as pontes formam as suas ligações para uma configuração x=A>0
(deslocação positiva)
x1
7. α é a probabilidade, por unidade de tempo, para a ligação das pontes e β é
a probabilidade, por unidade de tempo, para a separação das pontes.
A equação que descreve o modelo das pontes cruzadas é…
du
v
= βu
dx
Cuja solução permite determinar o comportamento da população de pontes…
u ( x) = αβ
exp( β ( x − A) / v)
v(α + β )
u(x)=0
Define-se ainda
se x<A
se x>A
p( x) = p1 (exp(γx) − 1) como a força numa única ponte
O programa em MATLAB é baseado nestas equações….
Gráficos obtidos:
Gráficos 1 e 2
Variação da densidade populacional e da força de
uma contracção ao longo do tempo.
À medida que a contracção se inicia, o número de células musculares recrutadas
para executar a ligação/separação vai aumentando até que atinge um plateau, que
corresponderá ao número máximo de células que se podem envolver no processo.
Numa fase inicial a força aumenta até um valor elevado, num período de
tempo que corresponderá à ligação, e diminui abruptamente quando deixa
de haver ligação.
Devido ao elevado número de células envolvidas, há sempre algumas que
ficam ligadas e isso contribui para que a força nunca se anule. Temos que
considerar a possibilidade de nestas células que foram experimentadas
estarem células antagonistas, que executam força no sentido contrário.
Gráfico 3
Variação da densidade populacional em
função da sua deslocação.
Todo este espaço de tempo corresponde a uma contracção
Comportamento Macroscópico: Balanço humano de um pêndulo invertido:
Será o tamanho da oscilação controlada pela impedância do tornozelo?
™ Podem indivíduos alterar sistematicamente
o tamanho da oscilação em resposta a uma
instrução e avaliação do feedback visual?
Se sim…
™ Será que os indivíduos diminuem o tamanho
da oscilação por aumento da impedância do
tornozelo ou por algum mecanismo alternativo?
Implementação em Simulink
Equação para o pêndulo
d 2θ
dθ
I 2 +b
− K tt senθ = Ttornozelo
dt
dt
Constantes
→ Inércia: I=62.6 Kg.m2
→ Factor de viscosidade: b=0.061 N.m.s.deg-1
Equação para a torção do tornozelo
− Ttornozelo
dθ
= k (θ − θ 0 ) + B
+ω
dt
→ Torção de oscilação gravitacional por unidade
angular: Ktt=10.3 N.m.deg-1
→ Viscosidade do tornozelo:
B=300 N.m.s.rad-1=6.11 N.m.s.deg-1.
→ Rigidez do tornozelo:
k=850+Ktt=1440 N.m.rad-1=25.1 N.m.deg-1
Gráfico Obtido:
Instante inicial→inclinação negativa(~-75º)
Máximo → 60º
Mínimo → -45º
Processo cíclico!
Gráfico 4 -Variação do ângulo de torção
com o tempo
Portanto…
O indivíduo ao concentrar-se consegue travar o movimento muscular.
Partindo do feedback visual, que é processado no cérebro e transmitido por resposta
neuronal aos músculos, consegue aumentar a resposta à torção e,consequentemente,
diminuir o respectivo ângulo.