MATEMÁTICA

UDESC
2012/2
MATEMÁTICA
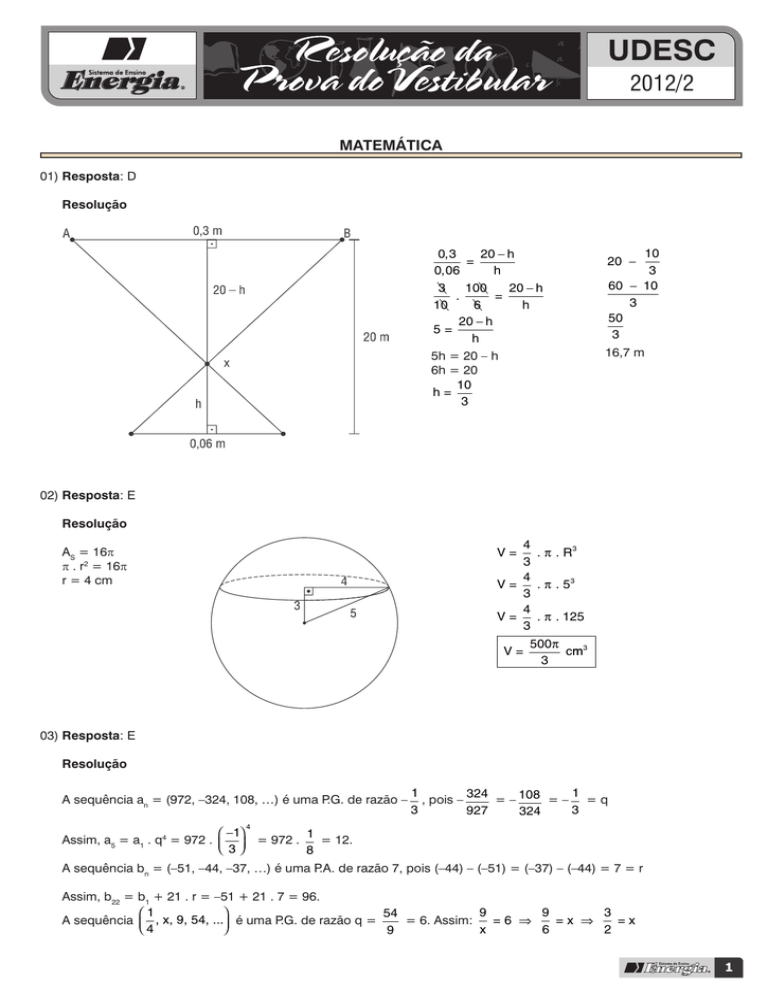
01)Resposta: D
Resolução
0, 3
20 − h
=
0, 06
h
100
20 − h
3
.
=
10
6
h
20 − h
5=
h
5h = 20 – h
6h = 20
10
h=
3
10
3
60 − 10
3
50
3
20 −
16,7 m
02)Resposta: E
Resolução
4
. π . R3
3
4
V=
. π . 53
3
4
V=
. π . 125
3
AS = 16π
π . r2 = 16π
r = 4 cm
V=
V=
500π
m3
cm
3
03)Resposta: E
Resolução
A sequência an = (972, –324, 108, …) é uma P.G. de razão –
1
1
324
, pois –
= – 108 = – = q
3
3
927
324
4
 −1
1
Assim, a5 = a1 . q4 = 972 .   = 972 .
= 12.
 3
8
A sequência bn = (–51, –44, –37, …) é uma P.A. de razão 7, pois (–44) – (–51) = (–37) – (–44) = 7 = r
Assim, b22 = b1 + 21 . r = –51 + 21 . 7 = 96.
9
9
3
1

54
=6 ⇒
=x ⇒
=x
A sequência  , x, 9, 54, ... é uma P.G. de razão q =
= 6. Assim:
4

x
6
2
9
1
UDESC
2012/2
3

Agora, a nova progressão será formada por: (x, a5, b22) =  , 12, 96 .
2

3
Esta sequência é uma P.G., pois 122 =
. 96 (satisfazem a propriedade do termo central em uma P.G.) e a sua razão
2
96
vale q =
⇒ q = 8.
12
04)Resposta: A
Resolução
60 ± ( −60)2 − 4 . 4 . 29
2.4
60 ± 56
x=
8
x' = 14,5 → Não poderia, pois as dimensões ficariam negativas.
1
x" =
2
x=
(18 – 2x) . (12 – 2x) = 187
216 – 36x – 24x + 4x2 = 187
4x2 – 60x + 29 = 0
05)Resposta: B
Resolução
Custo inicial: CT = 100 . 35,00 + 50 . 80,00 = 7500,00
Cadeiras alugadas por dia: 80% de 100 = 80
Guarda-sóis alugados por dia: 80% de 50 = 40
Das 80 cadeiras, x são retiradas e dos 40 guarda-sóis x
também são retirados para formar o conjunto "cadeira e
guarda-sol". Assim temos x conjuntos "cadeira e guardasol".
Assim, a P.A. é dada por (50, 30, 10)
Cálculo do faturamento diário:
Fd = 50 . 5,00 + 30 . 13,00 + 10 . 10,00 = 740,00
De 15/12/2011 a 15/03/2012 tem 92 dias (2012 é bissexto).
O faturamento total foi de:
P.A. (80 – x, x, 40 – x)
Pela propriedade do termo central:
FT = 92 . 740,00 = 68080,00
O lucro então é dado por:
(80 − x ) + (40 − x )
x=
2
2x = –2x + 120
4x = 120 ⇒ x = 30
2
L = 68080,00 – 7500,00
L = 60580,00
UDESC
2012/2
06)Resposta: E
Resolução
ATotal = AB + Ab + A
(8 + 2) . 4
AT = 82 + 22 + 4 .
2
AT = 64 + 4 + 80
AT = 148 cm2
07)Resposta: C
Resolução
Total: 5000
Gastronomia ⇒ 52% de 5000 = 2600
Entretenimento ⇒ 44% de 5000 = 2200
Saúde e beleza ⇒ 46% de 5000 = 2300
Por diagramas:
Exatamente um dos três:
(1400) + (1400 – x) + (1600 – x)
1400
+ 1400 −600
+ 1600 − 600
3200
08)Resposta: C
Resolução
cos2 (2x) – sen2 x = cos6 (x) → soma das soluções ? → x ∈ [0, 2π]
(cos2 x – sen2 x)2 – (1 – cos2 x) = cos6 x
cos4 x – 2 cos2 x . sen2 x + sen4 x – 1 + cos2 x = cos6 x
cos4 x – 2 cos2 x (1 – cos2 x) + (1 – cos2 x)2 – 1 + cos2 x = cos6 x
cos4 x – 2 cos2 x + 2 cos4 x + 1 – 2 cos2 x + cos4 x – 1 + cos2 x = cos6 x
cos6 x –4 cos4 x + 3 cos2 x = 0 → cos2 x = y
y3 – 4y2 + 3y = 0
y . (y2 – 4y + 3) = 0
y = 0 ou y2 – 4y + 3 = 0
y' = 3
y" = 1
3
UDESC
2012/2

x =
2
cos x = 0 → cos x = 0 → 
x =

π
2
3π
2
x = 0

cos x = 1 → cos x = ±1 → x = π
 x = 2π

2
cos2 x = 3 → cos x = ± 3 → ∃/ x
0 + π + 2π +
π
3π
+
= 5π
2
2
09)Resposta: B
Resolução
det A . det B + det (B + I) = 22 det Bt → (det(k . An) = kn . det A) e det At = det A
 3 2
 1 0
 4 2
+ 
= 
det A . det B + det (B + I) = 4 det B → B + I = 


 1 1
 0 1
 1 2
(–x(x + 1) – 2x2) . (3 – 2) + (8 – 2) = 4(3 – 2) → –x2 – x – 2x2 + 6 = 4 → –3x2 – x + 2 = 0
2
2
x
x2 +
–
= 0 (x2 – Sx + P = 0) → p = –
3
3
3
10)Resposta: A
Resolução
A – 6B = C – desta igualdade, temos:
9x – 6 . 3x = 27 → 32x – 6 . 3x – 27 = 0 → fazendo 3x = K, temos:
k2 – 6k – 27 = 0 → K = 9 ou K = –3. Logo, 3x = 9 → 3x = 32 → x = 2
a – 6b = 13, mas temos também que: 4 – 6 = b → b = –2 → a – 6(–2) = 13 → a = 1
–1 – 6 . 2–1 = c → c = –4
16y – 6 . 42y – 1 = 22y – 1 – 10 → 42y – 6 . 42y . 4–1 – 22y . 2–1 + 10 = 0
Fazendo 22y = R → R2 + R – 20 = 0 → R = 4 ou R = –5 → R = 4 → 22y = 4 → y = 1
Portanto, x2 + y2 + a2 + b2 + c2 → 22 + 12 + 12 + (–2)2 + (–4)2 = 26
4
UDESC
2012/2
11)Resposta: D
Resolução
Vera pode montar sua dieta das seguintes maneiras:
1)Com 3 frutas diferentes
C37 =
2) Com duas frutas iguais
7!
= 35
3!4!
Exemplo:
Como temos 7 possibilidades de escolhermos 2 frutas iguais e sempre
completá-las de 6 formas, o total de grupos será dado por 7 . 6 = 42
Logo, Vera terá 35 + 42 = 77 maneiras diferentes de montar a dieta.
12)Resposta: D
Resolução
Cálculo do resto:
Agora, como f(x) = 2x + k, então f(g(x)) = 2g(x) + k
Substituindo na igualdade f(g(x)) = r(x), temos:
2g(x) + k = 5x + 7
5x + 7 − k
g(x) =
2
Resolvendo a inequação g(x) ≥ 10, obtemos:
k + 13
5x + 7 − k
≥ 10 ⇒ 5x + 7 – k ≥ 20 ⇒ 5x ≥ k + 13 ⇒ x ≥
5
2
Como o conjunto solução é dado por{x ∈ R/x ≥ 3}, então:
k + 13
=3
5
k=2
13)Resposta: B
Resolução
EM DESENVOLVIMENTO
5
UDESC
2012/2
14)Resposta: C
Resolução
Domínio de f(x) =
x
x3 − 1
x
≥ 0
x − 1
3
Domínio de f(x) =
1
1 − |x|
1 – |x| > 0
–|x| > – 1
|x| < 1 ⇒ –1 < x < 1
D = {x ∈ R/–1 < x < 1}
Domínio de f(x) = tg (2x)
π
2x ≠ + k . π
2
π
π
x ≠
+k.
4
2
π 1

x ≠
.  + k

2 2
x ≠
 1 
Domínio de f(x) = sen 
 x − 1
x–1≠0⇒x≠1
D = {x ∈ R/x ≠ 1}
π  1 + 2k 
. 

2  2 
(2k + 1) . π


D = x ∈ R/x ≠
, k ∈ Z
4


Domínios coerentes: D = {x ∈ R/x ≠ 1}; D = {x ∈ R/x ≤ 0 ou x > 1}; D = {x ∈ R/–1 < x < 1}
15)Resposta: A
Resolução
sen 60o =
sen 30o =
sen 30o =
y
3
=
2
2
y
1
=
2
2
y=1
1
y
=
1
2
cos 60o =
x
1
=
2
2
cos 30o =
x
3
=
2
2
cos 30o =
3
x
=
1
2
3 ≅ 1,7
6
UDESC
2012/2
d2AB = ( 3 − 1)2 + ( 3 − 1)2 = 3 − 2 3 + 1 + 3 − 2 3 + 1 = 8 − 4 3 ≅ 8 − 6,8 = 1,2
2
2

3
1

d2AC =  1 −
−
+
3

 =1 −
2 
2

3+
3
+3 −
4
3+
1
= 5 − 2 3 ≅ 5 − 3,4 = 1,6
4
2
2

3
1
3
1

2
−
dBC
= 3 −
+
1
+
= 10 − 3 3 ≅ 10 − 5,,1 = 4,9

 = 9 − 3 3 +

2
2
4
4


O triângulo é escaleno.
7