Medidas de Tendência Central e de Variação

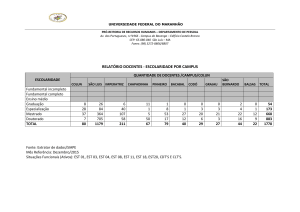
Est. Apl. Agric.
Medidas de tendência central e variação
2011-1
Variação do acaso
A variação que não se deve a qualquer causa conhecida
Exemplos
◦
Os tempos gastos por um mesmo motorista, em um mesmo carro para um mesmo percurso
◦
Os resultados de um mesmo aluno em uma mesma prova
◦
As alturas de vários irmãos criados e alimentados do mesmo modo
◦
A produção de várias plantas de uma mesma parcela
Ou seja, essencialmente qualquer medida do mundo real
População x amostra
População
Amostra
Todo o universo
Uma parte do universo, que o representa
Após medida, não muda mais
Outra amostra da mesma população terá resultados
diferentes
Qualquer conclusão só vale para esta população
A conclusão feita com base na amostra deve representar
toda a população
Qualquer medida é um parâmetro
Toda medida é uma estimativa
Exemplos
◦
Considerar os alunos de uma turma como população ou amostra
◦
Considerar a produção de uma cultivar como amostra de uma possível população
Tendência central
Importante para sintetizar os dados da amostra
Indica o “miolo” dos dados
Principais medidas
◦
Moda
◦
Mediana
◦
Média
◦
Para distribuições assimétricas, usar mediana e média
Vantagem
Desvantagem
Simples
Moda
Não é sensível a valores extremos
Adequada para dados qualitativos
Pode existir ou não
Não leva os demais valores em consideração
Sempre existe
Mediana
Reflete os valores no centro da distribuição
Não reflete todos os valores
Não é sensível a valores extremos
Média
Ponto de equilíbrio para distribuição de
freqüências
Sensível a valores extremos
Leva todos os valores em consideração
Universidade Federal Rural de Pernambuco
[Autor]
1
Est. Apl. Agric.
Medidas de tendência central e variação
2011-1
Medidas de variação
Importantes para complementar as informações sobre a amostra
Dão uma ideia da “abertura” dos dados em torno da tendência central
Variação
◦
Amplitude
◦
Variância (s²)
◦
Desvio padrão (s)
◦
Corresponde ao valor médio dos desvios de cada ponto em relação à média
◦
Geralmente a maioria dos pontos fica a um desvio-padrão da média
n
soma dos desvios²   ponto  média ² i
s² 


grau de liberdade
n 1
x
i
  x²   x²

x²
n 1
n 1
Coeficiente de variação
CV 
s
100
x
Grau de liberdade
◦
Conseqüência direta de trabalhar com amostra
◦
É o número de pontos completamente independentes
◦
Calculado como o número de pontos da amostra (n) subtraindo o número de valores calculados com esta
amostra antes deste ponto
◦
Normalmente n-1, já que sempre precisamos calcular a média
Intervalo de confiança
É uma medida do intervalo em que provavelmente o valor da população se encontra
◦
Leva em consideração uma margem de erro (nível de confiança nas conclusões)
◦
O valor t0 da equação abaixo é encontrado na tabela de t, com n-1 graus de liberdade
mˆ  to
s
n
Universidade Federal Rural de Pernambuco
[Autor]
2
Est. Apl. Agric.
Medidas de tendência central e variação
2011-1
Tabela t
0,10
0,05
0,01
1
6,314
12,706
63,657
2
2,920
4,303
9,925
3
2,353
3,182
5,841
4
2,132
2,776
4,604
5
2,015
2,571
4,032
6
1,943
2,447
3,707
7
1,895
2,365
3,499
8
1,860
2,306
3,355
9
1,833
2,262
3,250
10
1,812
2,228
3,169
15
1,753
2,131
2,947
20
1,725
2,086
2,845
30
1,697
2,042
2,750
40
1,684
2,021
2,704
50
1,676
2,009
2,678
100
1,660
1,984
2,626
1000
1,646
1,962
2,581
Quantos mais pontos (maior grau de liberdade) menor a faixa de valores em torno da média
Graus de liberdade
Chance de errar
Menor chance de erro, maior faixa de valores em torno da
média
Valores calculados utilizando o Excel.
◦
Qualquer outra planilha tem função equivalente
=invt(probabilidade;graus de liberdade)
Interpolação harmônica
◦
Usada quando o GL que você quer não está em uma tabela
◦
Para GLA e GLB existentes na tabela com tA e tB, querendo GLC que não está na tabela
◦
Diminuiu a importância com fórmulas estatísticas nas planilhas
Universidade Federal Rural de Pernambuco
[Autor]
3
Est. Apl. Agric.
GLB  GLA  tA  tB
GLB  GLC  tC  tB
Medidas de tendência central e variação
2011-1
 GLB  GLC  tA  tB  
tC  
  tB
GLB  GLA


Exemplo – Queremos o valor de t para 5% de probabilidade com 75 GL
100  50  2,009  1,984
100  75  tC  1,984
 25  0,025 
tC  
  1,984  1,9965
50


Usando o Excel
=invt(0,05;75)= 1,992102124
A diferença vem em parte de arredondamentos, e em parte inerente à interpolação.
◦
Evitar sempre que possível. Quando necessário usar o menor intervalo possível para os GL
Apresentação típica de resultados
4,0
3,5
3,0
2,5
2,0
1,5
1,0
0,5
0,0
Preto
Carioca
Branco
Rajado
IPA8
Princesa
Figura 1 - Matéria seca da parte aérea de diferentes cultivares de feijoeiro em casa de vegetação. Barras verticais correspondem ao
erro padrão da média
Universidade Federal Rural de Pernambuco
[Autor]
4