Divisão e conquista

Agenda
Análise e Técnicas de Algoritmos
••
••
••
Conceitos
Conceitos Básicos
Básicos
Template
TemplateGenérico
Genérico
Exemplos
Exemplos
Jorge Figueiredo
Divisão
Divisão ee Conquista
Conquista
© Jorge Figueiredo, DSC/UFCG
Análise e Técnicas de Algoritmos – 2005.1
© Jorge Figueiredo, DSC/UFCG
Análise e Técnicas de Algoritmos – 2005.1
Motivação
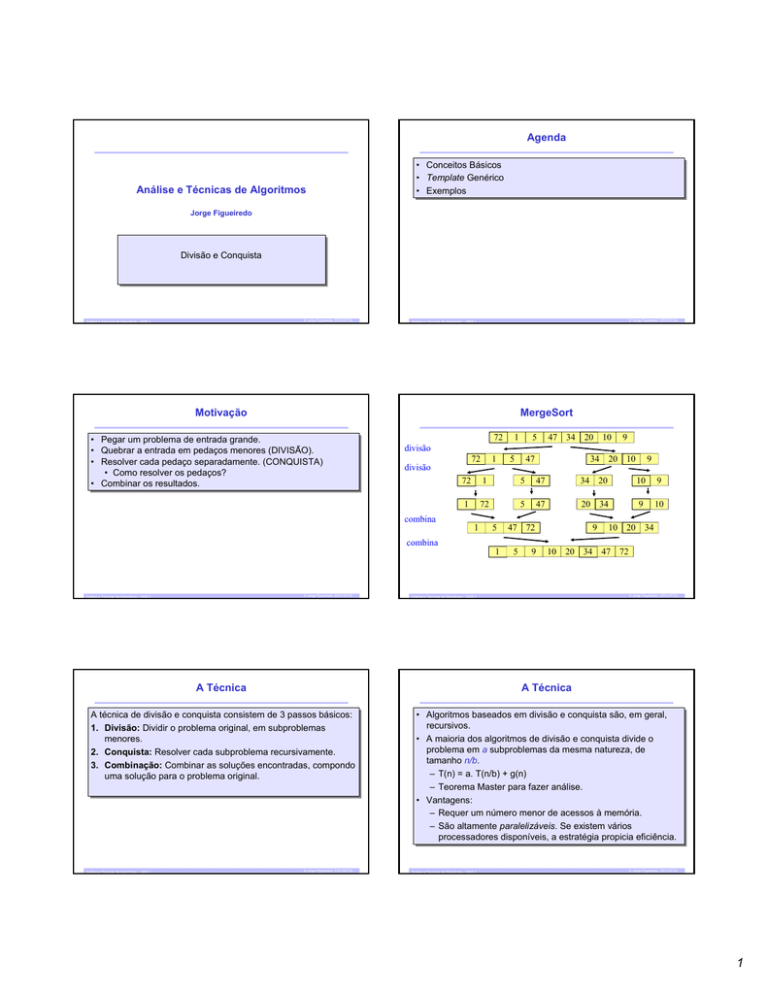
MergeSort
••
••
••
Pegar
Pegar um
um problema
problema de
de entrada
entrada grande.
grande.
Quebrar
Quebrar aa entrada
entrada em
em pedaços
pedaços menores
menores (DIVISÃO).
(DIVISÃO).
Resolver
Resolver cada
cada pedaço
pedaço separadamente.
separadamente. (CONQUISTA)
(CONQUISTA)
•• Como
Como resolver
resolver os
ospedaços?
pedaços?
•• Combinar
Combinar os
os resultados.
resultados.
72
72
divisão
combina
© Jorge Figueiredo, DSC/UFCG
47 34 20 10
9
1
5
47
34 20 10
9
1
5
47
34 20
10
9
1
72
5
47
20 34
9
10
1
5
1
47 72
5
9
9
10 20 34
10 20 34 47 72
© Jorge Figueiredo, DSC/UFCG
Análise e Técnicas de Algoritmos – 2005.1
A Técnica
A Técnica
AAtécnica
técnica de
de divisão
divisão ee conquista
conquista consistem
consistem de
de 33 passos
passosbásicos:
básicos:
1.
1. Divisão:
Divisão: Dividir
Dividir oo problema
problema original,
original, em
em subproblemas
subproblemas
menores.
menores.
2.
2. Conquista:
Conquista: Resolver
Resolver cada
cada subproblema
subproblema recursivamente.
recursivamente.
3.
3. Combinação:
Combinação: Combinar
Combinar as
as soluções
soluções encontradas,
encontradas, compondo
compondo
uma
uma solução
solução para
para oo problema
problema original.
original.
Análise e Técnicas de Algoritmos – 2005.1
5
72
combina
Análise e Técnicas de Algoritmos – 2005.1
1
divisão
© Jorge Figueiredo, DSC/UFCG
•• Algoritmos
Algoritmos baseados
baseados em
em divisão
divisão ee conquista
conquista são,
são, em
em geral,
geral,
recursivos.
recursivos.
•• AA maioria
maioria dos
dos algoritmos
algoritmos de
de divisão
divisão ee conquista
conquista divide
divide oo
problema
problema em
em aa subproblemas
subproblemas da
da mesma
mesma natureza,
natureza, de
de
tamanho
tamanho n/b.
n/b.
–– T(n)
T(n) == a.
a. T(n/b)
T(n/b) ++ g(n)
g(n)
–– Teorema
Teorema Master
Master para
para fazer
fazer análise.
análise.
•• Vantagens:
Vantagens:
–– Requer
Requer um
um número
número menor
menor de
de acessos
acessos àà memória.
memória.
–– São
São altamente
altamente paralelizáveis.
paralelizáveis. Se
Se existem
existem vários
vários
processadores
processadores disponíveis,
disponíveis, aa estratégia
estratégia propicia
propicia eficiência.
eficiência.
Análise e Técnicas de Algoritmos – 2005.1
© Jorge Figueiredo, DSC/UFCG
1
Quando Utilizar DeC?
Quando Utilizar DeC?
Existem
Existem três
trêscondições
condições que
que indicam
indicam que
que aa estratégia
estratégia de
de divisão
divisão ee
conquista
conquista pode
pode ser
ser utilizada
utilizada com
comsucesso:
sucesso:
1.
1. Deve
Deve ser
ser possível
possível decompor
decompor uma
uma instância
instância em
em subsubinstâncias.
instâncias.
2.
2. AA combinação
combinação dos
dos resultados
resultados deve
deve ser
ser eficiente.
eficiente.
3.
3. As
Assub-instâncias
sub-instânciasdevem
devem ser
ser mais
mais ou
ou menos
menos do
do mesmo
mesmo
tamanho.
tamanho.
© Jorge Figueiredo, DSC/UFCG
Análise e Técnicas de Algoritmos – 2005.1
ÉÉ possível
possível identificar
identificar pelo
pelo menos
menos duas
duassituações
situações genéricas
genéricas em
em
que
que aa abordagem
abordagem por
por divisão
divisão ee conquista
conquista éé adequada:
adequada:
1.
1. Problemas
Problemas onde
onde um
um grupo
grupo de
de operações
operações são
são
correlacionadas
correlacionadas ou
ou repetidas.
repetidas. AA multiplicação
multiplicação de
de matrizes,
matrizes,
que
que veremos
veremos aa seguir,
seguir, éé um
um exemplo
exemplo clássico.
clássico.
2.
2. Problemas
Problemas em
em que
que uma
uma decisão
decisão deve
deve ser
sertomada
tomada e,
e, uma
uma
vez
vez tomada,
tomada, quebra
quebra oo problema
problema em
em peças
peças disjuntas.
disjuntas. Em
Em
especial,
especial, aa abordagem
abordagem por
por divisão-e-conquiasta
divisão-e-conquiasta éé
interessante
interessante quando
quando algumas
algumas peças
peças passam
passam aa ser
ser
irrelevantes.
irrelevantes.
© Jorge Figueiredo, DSC/UFCG
Análise e Técnicas de Algoritmos – 2005.1
Algoritmo Genérico
Exemplo 1
DivisãoeConquista(x)
if x é pequeno ou simples do
return resolver(x)
else
decompor x em conjuntos menores x0, x1, … xn
for i ← 0 to n do
yi ← DivisãoeConquista(xi)
i ← i +1
combinar yi’s
return y
© Jorge Figueiredo, DSC/UFCG
Análise e Técnicas de Algoritmos – 2005.1
•• OOproblema
problemaconsiste
consisteem
emencontrar
encontraroomaior
maiorelemento
elementode
deum
umarray
arrayA[1..n]
A[1..n]
Solução Ingênua
Maxim(A[1..n])
max ← A[1]
for i ← 2 to n do
if A[j] > max then
max ← A[i]
return max
Exemplo 1
Exemplo 2
•• OOproblema
problemaconsiste
consisteem
emencontrar
encontraroomaior
maiorelemento
elementode
deum
umarray
arrayA[1..n]
A[1..n]
Solução Ingênua
Maxim(A[1..n])
maior ← A[1]
for i ← 2 to n do
if A[j] > maior then
maior ← A[i]
return maior
Análise e Técnicas de Algoritmos – 2005.1
© Jorge Figueiredo, DSC/UFCG
Análise e Técnicas de Algoritmos – 2005.1
n
•• OOproblema
problemaconsiste
consisteem
emcomputa
computaaan,,em
emque
quenn∈∈N.
N.
Solução Ingênua
Solução DeC
Maxim(A[x..y])
if x – y ≤ 1 then
return max(A[x], A[y])
else
m ← x+y/2
v1 ← Maxim(A[x..m])
v2 ← Maxim(A[m+1..y])
return max(v1, v2)
© Jorge Figueiredo, DSC/UFCG
Pow(a, n)
p←a
for i ← 2 to n do
p←p×a
return p
Análise e Técnicas de Algoritmos – 2005.1
Solução DeC
Pow(a, n)
if n=0 then
return 1
if n é par then
return Pow(a, n/2) × Pow(a, n/2)
else
return Pow(a,n-1/2) × Pow(a, n-1/2) × a
© Jorge Figueiredo, DSC/UFCG
2
Multiplicação de Inteiros Grandes
Multiplicação de Inteiros Grandes
•• O
O problema
problema consiste
consiste em
em multiplicar
multiplicar dois
dois números
números inteiros
inteiros
grandes.
grandes.
•• AA multiplicação
multiplicação clássica
clássica(a
(a que
que aprendemos
aprendemos fazer
fazer na
na escola)
escola)
2
requer
requer tempo
tempo Θ(n
Θ(n2).). Isso
Issoporque
porque fazemos
fazemos multiplicação
multiplicaçãodígito
dígito
aa dígito.
dígito.
n
Solução
Solução Alternativa
Alternativa por
por Divisão
Divisão ee Conquista
Conquista
•• Para
Para evitar
evitar maiores
maiorescomplicações,
complicações, vamos
vamos assumir
assumir que
que oo
número
número de
de dígitos
dígitos em
em cada
cada número
número éé potência
potência de
de 2.
2.
•• AA multiplicação
multiplicação de
de um
um número
número AA por
por um
um número
número BB pode
pode ser
ser
efetuada
efetuada dividindo-se
dividindo-se oo número
número original
original em
em dois
dois super-dígitos
super-dígitos
ee procedendo
procedendo aa multiplicação
multiplicação ..
Análise e Técnicas de Algoritmos – 2005.1
© Jorge Figueiredo, DSC/UFCG
n/2
n/2
A:
w
x
B:
y
z
wz
xz
wy
xy
wy
wz + xy
Análise e Técnicas de Algoritmos – 2005.1
Multiplicação de Inteiros Grandes
xz
© Jorge Figueiredo, DSC/UFCG
Multiplicação de Inteiros Grandes
2m
m
Mult(A,B)
Mult(A,B)==Mult(w,y).10
Mult(w,y).102m++ (Mult(w,z)+Mult(x,y)).10
(Mult(w,z)+Mult(x,y)).10m++ Mult(x,z)
Mult(x,z)
Uma
Uma solução
solução por
por divisão
divisão ee conquista:
conquista:
m
•• AA multiplicação
pode ser
ser vista
vista como
como oo deslocamento
deslocamento
multiplicação por
por 10
10mpode
de
de m
m posições
posições para
para aa direita.
direita.
•• As
As adições
adições envolvidas
envolvidas tomam
tomam tempo
tempoΘ(n)
Θ(n) cada.
cada.
•• AA multiplicação
multiplicação de
de dois
dois inteiros
inteiros longos
longos éé oo resultado
resultado de
de 44
produtos
produtos de
de inteiros
inteiros de
de tamanho
tamanho metade
metade do
do valor
valor original,
original, ee
um
um constante
constante número
número de
de adições
adições ee deslocamentos,
deslocamentos, com
com
tempo
tempo Θ(n).
Θ(n).
1.
1. Divisão:
Divisão: Dividir
Dividir cada
cada número
número em
em dois
dois números
números com
com
metade
metade da
da quantidade
quantidade de
de dígitos.
dígitos.
2.
2. Conquista:
Conquista: Proceder
Proceder aa multiplicação
multiplicação das
das quatro
quatro partes.
partes.
3.
3. Combinação:
Combinação: Combinar
Combinar os
os resultados
resultados com
com deslocamento
deslocamento
ee adições.
adições.
AA análise
análise do
do algoritmo
algoritmo que
que utiliza
utiliza divisão
divisão ee conquista
conquista requer
requer aa
solução
solução da
da seguinte
seguinte relação
relação de
de recorrência:
recorrência:
–– T(n)
T(n) == 4.T(n/2)
4.T(n/2) ++ Θ(n)
Θ(n)
2
–– Θ(n
Θ(n2))
Análise e Técnicas de Algoritmos – 2005.1
© Jorge Figueiredo, DSC/UFCG
Análise e Técnicas de Algoritmos – 2005.1
Multiplicação de Inteiros Grandes
Uma
Uma Solução
Soluçãopor
porDivisão
Divisão ee Conquista
Conquista Mais
Mais Eficiente
Eficiente
–– Por
que
não
temos
a
eficiência
desejada?
Por que não temos a eficiência desejada? Ora,
Ora, temos
temos 44
multiplicaçõs
multiplicaçõs de
de números
números de
de tamanho
tamanho n/2.
n/2.
–– AA solução
solução seria
seria reduzir
reduzir oo número
número de
de multiplicações?
multiplicações? Isso
Isso
éé verdade
verdade pois
pois sabemos
sabemos que
que aa adição
adição ee deslocamentos
deslocamentos
contribui
contribui com
com Θ(n).
Θ(n).
–– Se
Se observarmos
observarmos mais
mais detalhadamente,
detalhadamente, podemos
podemos reduzir
reduzir
para
para três
três oo número
número de
de multiplicações:
multiplicações:
•• C=
C= wy
wy
•• D=
D= xz
xz
•• E=
E= (wz
(wz ++xy)
xy)
Análise e Técnicas de Algoritmos – 2005.1
© Jorge Figueiredo, DSC/UFCG
© Jorge Figueiredo, DSC/UFCG
Multiplicação de Inteiros Grandes
••
••
••
••
C=
C= Mult(w,y)
Mult(w,y)
D=
D= Mult(x,z)
Mult(x,z)
E=
E=Mult((w+x,
Mult((w+x, y+z))
y+z)) –– CC –– DD ==(wy+wz+xy+xz)-wy-xz=(wz
(wy+wz+xy+xz)-wy-xz=(wz ++ xy)
xy)
2m
m
Logo,
Logo, Mult(A,B)
Mult(A,B) ==C.10
C.102m++ E.10
E.10m++DD
•• No
No total,
total,fazemos
fazemos33 multiplicações,
multiplicações, 44adições
adições ee 22 subtrações
subtrações
de
de números
números com
com n/2
n/2 dígitos.
dígitos.ÉÉ necessário
necessário ainda
ainda fazer
fazer
deslocamentos
deslocamentos mas,
mas,tudo
tudo isso
issorepresenta
representa Θ(n).
Θ(n).
•• T(n)
T(n) == 3.T(n/2)
3.T(n/2) ++ Θ(n)
Θ(n)
1.585
•• T(n)
T(n) éé Θ(n
Θ(n1.585))
Análise e Técnicas de Algoritmos – 2005.1
© Jorge Figueiredo, DSC/UFCG
3
Multiplicação de Matrizes
Algoritmo de Strassen
•Objetivo
•Objetivo éé multiplicar
multiplicar duas
duas matrizes
matrizes n×n.
n×n.
•Por
•Por exemplo,
exemplo, no
no caso
caso de
de n=2,
n=2, éé necessário
necessário efetuar
efetuar 88
8
x
multiplicações.
multiplicações. (2
(2x,, em
em que
que xx== log
log228))
•• Strassen
Strassen mostrou
mostrou que
que um
um multiplicação
multiplicação de
de matrizes
matrizes 2x2
2x2 pode
pode
ser
ser feita
feitacom
com 77 multiplicações
multiplicações ee 18
18 operações
operações de
de adição
adição ee
log 7
2.807
subtração.(2
subtração.(2log227 =2
=22.807))
•• Redução
Redução feita
feita usando
usando divisão
divisão ee conquista.
conquista.
×
A
C11 = a11b11 + a12b21
C12 = a11b12 + a12b22
A0
A1
C21 = a21b11 + a22b21
A2
A3
×
B
=
B0
B1
B2
B3
=
R
A0×B0+A1×B2
A0×B1+A1×B3
A2×B0+A3×B2
A2×B1+A3×B3
C22 = a21b12 + a22b22
© Jorge Figueiredo, DSC/UFCG
Análise e Técnicas de Algoritmos – 2005.1
Algoritmo de Strassen
P1 = (A11+ A22)(B11+B22)
P2 = (A21 + A22) * B11
P3 = A11 * (B12 - B22)
P4 = A22 * (B21 - B11)
P5 = (A11 + A12) * B22
P6 = (A21 - A11) * (B11 + B12)
P7 = (A12 - A22) * (B21 + B22)
Algoritmo de Strassen
C11 = P1 + P4 - P5 + P7
= (A11+ A22)(B11+B22) + A22 * (B21 - B11) - (A11 + A12) * B22+
(A12 - A22) * (B21 + B22)
= A11 B11 + A11 B22 + A22 B11 + A22 B22 + A22 B21 – A22 B11 A11 B22 -A12 B22 + A12 B21 + A12 B22 – A22 B21 – A22 B22
= A11 B11 + A12 B21
C11 = P1 + P4 - P5 + P7
C12 = P3 + P5
C21 = P2 + P4
C22 = P1 + P3 - P2 + P6
© Jorge Figueiredo, DSC/UFCG
Análise e Técnicas de Algoritmos – 2005.1
Menor Distância Entre Pontos
Análise e Técnicas de Algoritmos – 2005.1
© Jorge Figueiredo, DSC/UFCG
Menor Distância Entre Pontos
•• Distância
Distância Euclideana
Euclideana
y1
© Jorge Figueiredo, DSC/UFCG
Análise e Técnicas de Algoritmos – 2005.1
Closest Pair
Entrada: Um conjunto de pontos n P = <p1, p2, ..., pn›, em duas
dimensões.
Saída: O par de pontos p1 e p2 que apresenta a menor distância
euclideana.
(x1 , y1 )
( x2 , y 2 )
y2
x1
x2
(x1 , y1 ) − (x2 , y2 )
Análise e Técnicas de Algoritmos – 2005.1
=
(x1 − x2 )2 + ( y1 − y2 )2
© Jorge Figueiredo, DSC/UFCG
Análise e Técnicas de Algoritmos – 2005.1
© Jorge Figueiredo, DSC/UFCG
4
Menor Distância Entre Pontos
Menor Distância Entre Pontos
d
Análise e Técnicas de Algoritmos – 2005.1
© Jorge Figueiredo, DSC/UFCG
Menor Distância Entre Pontos
Análise e Técnicas de Algoritmos – 2005.1
© Jorge Figueiredo, DSC/UFCG
Menor Distância Entre Pontos – 2D
•• Solução
Solução Força
Força Bruta
Bruta éé O(n
O(n22).).
•• Vamos
Vamos assumir:
assumir:
–– Não
Não existem
existem pontos
pontoscom
com aa mesma
mesmacoordenada
coordenada x.
x.
–– Não
Não existem
existem pontos
pontoscom
com aa mesma
mesmacoordenada
coordenada y.
y.
•Como
•Como dividir
dividir em
em sub-problemas?
sub-problemas?
–Ordenar
–Ordenar de
de acordo
acordo com
com aacoordenada
coordenada xxee dividir
dividir em
em duas
duas
partes:
partes: esquerda
esquerda ee direita.
direita.
•• Como
Como resolver
resolver este
este problema
problema considerando
considerando 1D?
1D?
•• ÉÉ possível
possível aplicar
aplicar Divisão
Divisão ee Conquista?
Conquista?
Análise e Técnicas de Algoritmos – 2005.1
© Jorge Figueiredo, DSC/UFCG
Menor Distância Entre Pontos – 2D
Análise e Técnicas de Algoritmos – 2005.1
© Jorge Figueiredo, DSC/UFCG
Menor Distância Entre Pontos – 2D
•• Resolver
Resolver recursivamente
recursivamente cada
cada sub-problema,
sub-problema, obtendo
obtendo ddl leeddr.r.
•• O
O que
que podemos
podemos observar?
observar?
–– Já
Já temos
temos aa menor
menor distância
distância em
em cada
cada uma
uma das
das partes.
partes.
–– Fazer
Fazer d=
d= min{
min{ddl l,,ddr}.r}.
–– Falta
Falta analisar
analisar distância
distância entre
entre pontos
pontosde
de sub-problemas
sub-problemas
distintos.
distintos.
–– Devemos
Devemos analisar
analisar todos
todos os
oscasos?
casos?
•• Somente
Somente pontos
pontos que
que se
se encontram
encontram em
em uma
uma faixa
faixa de
de
tamanho
tamanho 2d
2d em
em torno
torno da
da linha
linha divisória.
divisória.
Análise e Técnicas de Algoritmos – 2005.1
© Jorge Figueiredo, DSC/UFCG
Análise e Técnicas de Algoritmos – 2005.1
© Jorge Figueiredo, DSC/UFCG
5
Menor Distância Entre Pontos – 2D
Menor Distância Entre Pontos – 2D
•• Qual
Qual aa quantidade
quantidade de
de pontos
pontos que
que se
seencontram
encontram dentro
dentro da
da
faixa
faixa de
de tamanho
tamanho 2d?
2d?
–– Se
Se considerarmos
considerarmos um
um pp∈∈ PPl,l,todos
todos os
os pontos
pontos de
de PPrr que
que
devem
devem ser
ser considerados
considerados devem
devem estar
estar em
em um
um retângulo
retângulo RR
de
de dimensões
dimensões dd ××2d.
2d.
•• Como
Como determinar
determinar os
os seis
seis pontos?
pontos?
–– Projeção
Projeção de
de pontos
pontos nos
nos eixos
eixos xx ee y.
y.
–– Pode-se
Pode-se fazer
fazer isso
isso para
para todo
todo pp ∈P
∈Pl l eePPrr,, em
em O(n)
O(n) (pontos
(pontos
ordenados).
ordenados).
•• Relação
Relação de
de recorrência
recorrência éé T(n)=
T(n)= 2.T(n/2)
2.T(n/2) ++O(n)
O(n)
–– Sabemos
Sabemos que
que isso
isso éé O(n.log
O(n.log n)
n)
d
R
d
d
d
R
d
d
© Jorge Figueiredo, DSC/UFCG
Análise e Técnicas de Algoritmos – 2005.1
Análise e Técnicas de Algoritmos – 2005.1
© Jorge Figueiredo, DSC/UFCG
ClosestPair(P)
Pré-processamento
Construir Px e Py como listas ordenadas pelas
coordenadas x e y
Divisão
Quebrar P em Pl e Pr
Conquista
dl = ClosestPair(Pl)
dr = ClossetPair(Pr)
Combinação
d= min{dl, dr}
Determinar faixa divisória e pontos
Verificar se tem algum par com distância < d
Análise e Técnicas de Algoritmos – 2005.1
© Jorge Figueiredo, DSC/UFCG
6