ângulos b

Propaganda

ÂNGULOS DA CIRCUNFERÊNCIA
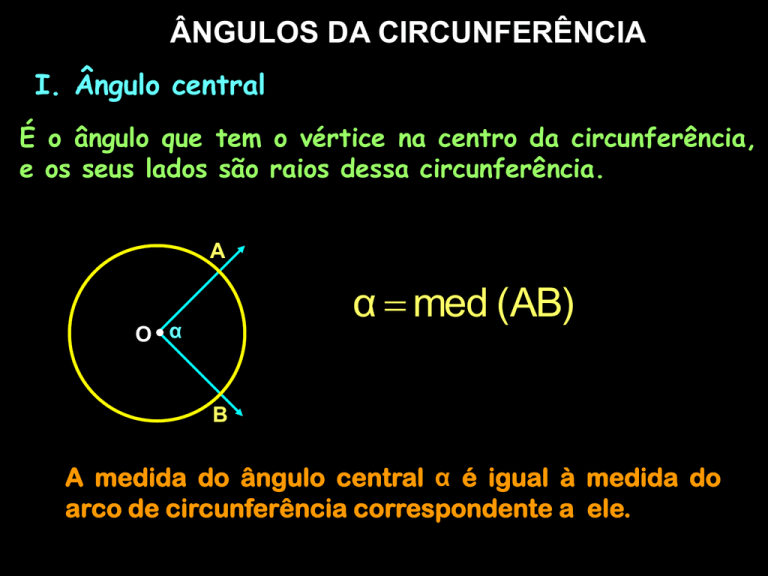
I. Ângulo central
É o ângulo que tem o vértice na centro da circunferência,
e os seus lados são raios dessa circunferência.
A
α  med (AB)
O α
B
A medida do ângulo central α é igual à medida do
arco de circunferência correspondente a ele.
ÂNGULOS DA CIRCUNFERÊNCIA
II. Ângulo inscrito
É o ângulo que tem o vértice na circunferência e os lados
são cordas dessa circunferência.
A
β
O α
B
med (AB)
β
2
α
β
2
A medida do ângulo inscrito β é igual à metade do ângulo
central determinado pelo mesmo arco de circunferência.
ÂNGULOS DA CIRCUNFERÊNCIA
II. Ângulo inscrito
Demonstração:
β
β
α
O
α
α  β  β  α  2β  β 
2
ÂNGULOS DA CIRCUNFERÊNCIA
II. Ângulo inscrito
Obs.:
α
α
M
O
α
N
O arco MN é chamado arco
capaz de α e mede 2α
ÂNGULOS DA CIRCUNFERÊNCIA
II. Ângulo inscrito
Obs.:
C
A
O
B
Todo triângulo inscrito numa semi-circunferência é
um triângulo retângulo
ÂNGULOS DA CIRCUNFERÊNCIA
II. Ângulo inscrito
Obs.:
A
α
O
D
B
β
C
Todo quadrilátero inscrito numa circunferência tem
ângulos opostos suplementares.
ÂNGULOS DA CIRCUNFERÊNCIA
III. Ângulo de segmento
É o ângulo que possui o vértice na circunferência, um dos
seus lados tangente a ela, e outro, secante.
O
A
α V
med (AV)
α
2
ÂNGULOS DA CIRCUNFERÊNCIA
III. Ângulo de segmento
Demonstração:
O
β
90  α
A
90  α
α V
90    90      180   




2
ÂNGULOS DA CIRCUNFERÊNCIA
IV. Ângulo excêntrico interior ou de vértice interno
É aquele que tem o vértice no interior da circunferência,
e seus lados são secantes a ela.
A
D
O
α
B
β
med(AB)  med(CD)
α
2
med(AD)  med(BC)
β
2
α
C
A medida do ângulo excêntrico interior é a media
aritmética dos seus arcos correspondentes.
ÂNGULOS DA CIRCUNFERÊNCIA
IV. Ângulo excêntrico interior ou de vértice interno
Demonstração:
A
D
O
α
β
P
B


2
2
C
α β
αβ
ˆ
ˆ
med(A PB)    med(A PB) 
2 2
2
ÂNGULOS DA CIRCUNFERÊNCIA
IV. Ângulo excêntrico exterior ou de vértice externo
É aquele que tem o vértice no exterior da circunferência,
e seus lados são secantes a ela.
A
D
α
O
C
B
P
med(AB)  med(CD)
α
2
A medida do ângulo excêntrico exterior é a metade da
diferença das medidas dos seus arcos correspondentes.
ÂNGULOS DA CIRCUNFERÊNCIA
IV. Ângulo excêntrico exterior ou de vértice externo
Demonstração:

2
A
α
D
O
β
P
C
B

2




 
 
ˆ
ˆ
med APB    med APB 
2 2
2