1. Elementos de Circuitos no domínio de Faso Introdução • Para

Campus I – João Pessoa
Disciplina: Análise
nálise de Circuitos
Curso
urso Técnico Integrado em Eletrônica
Profª: Rafaelle Feliciano
Aula 03 – Circuitos CA
1. Elementos de Circuitos no domínio de Fasores
Introdução
• Para compreender a resposta de dispositivos básicos R (resistor), L (indutor) e C (capacitor) a um
sinal senoidal → conceito de derivada
o
Derivada
o
o
Se não houver variação de x → derivada é nula
Derivada em um ponto é a inclinação da curva neste ponto
é a taxa de variação de x em relação ao tempo
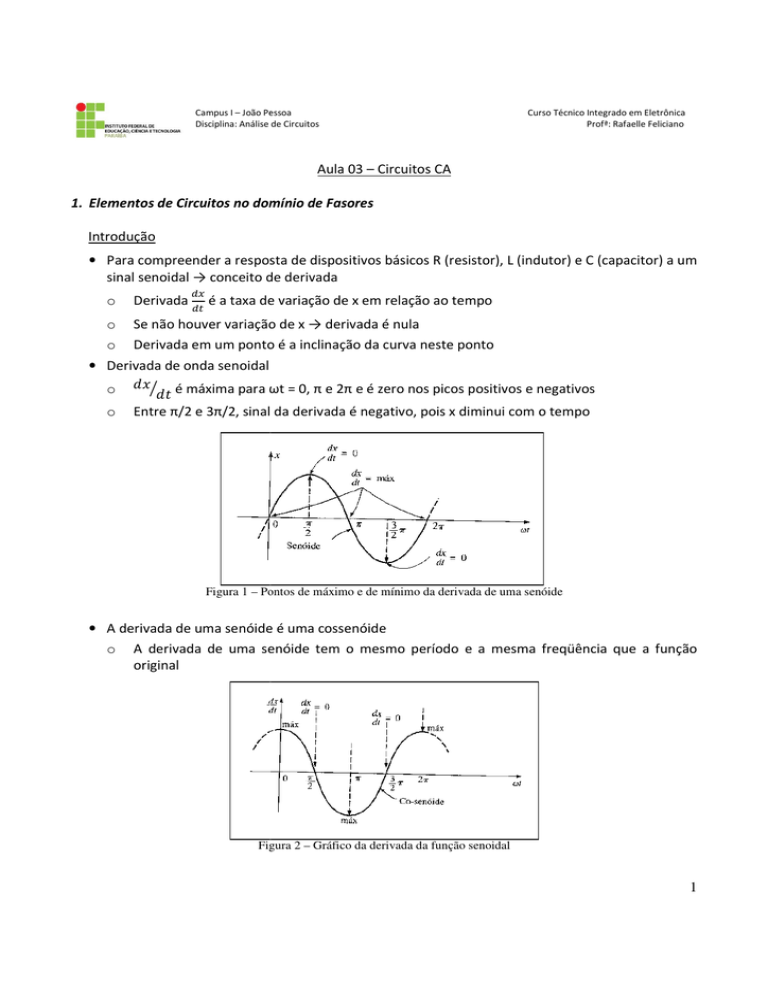
• Derivada de onda
nda senoidal
o é máxima
ma para ωt = 0, π e 2π e é zero nos picos positivos e negativos
o Entre π/2 e 3π/2, sinal
inal da
da derivada é negativo, pois x diminui com o tempo
Figura 1 – Pontos de máximo e de mínimo da derivada de uma senóide
• A derivada de uma
ma senóide é uma cossenóide
o A derivada de uma senóide tem o mesmo período e a mesma freqüência que a função
original
Figura 2 – Gráfico da derivada da função senoidal
1
Se Respostas dos elementos R, L e C a sinal senoidal
Resistor
• O valor da resistência não é influenciado por tensões ou correntes senoidais
o Para qualquer freqüência, R permanece constante
• Lei de Ohm pode ser aplicada para v(t) = Vmsen(ωt ± θ)
Então,
ou Ω
• Para elementos puramente resistivos
resistivos, a tensão e a corrente
orrente estão em fase
o A relação entre os valores de pico → Lei de Ohm
Figura 3 - Tensão e corrente senoidais em fase para elementos resistivos
Indutor
• Tensão
ão no indutor é diretamente proporcional à taxa de variação da corrente
cor
que o atravessa
o Quanto maior a freqüência f (Hz = Hertz), maior a taxa de variação da corrente e maior o
valor da tensão induzida
o Quanto maior a indutância L (H = Henry) no enrolamento, maior a taxa de variação do fluxo
magnético e maior a tensão no indutor
VL é proporcional a ωL
• Tensão no indutor
!
2
Figura 4 - Resposta do indutor a uma corrente senoidal
Como
" # Então,
!
!" # ! % 90( !
• Para um indutor ou elementos puramente indutivos,
indutivos a tensão vL está
stá adiantada de 90o em
relação à corrente iL
o
Ou iL está atrasada de 90o em relação a vL
Figura 5 – Tensão senoidal
s
adiantada de 90o em relação à corrente para indutor puro
• Reatância Indutiva
$ o
o
! (ohms, Ω)
Definida pela Lei de Ohm
Reatância indutiva é oposição à corrente, mas não dissipa energia elétrica → troca de
energia entre fonte e campo magnético do indutor
Capacitor
• Tensão no capacitor é limitada pela taxa com que a carga é depositada nas placas do capacitor
3
o
o
o
Variação instantânea da tensão no capacitor sofre oposição, pois é necessário um tempo
para carregar ou descarregar as placas do capcitor (V=Q/C)
Quanto maior a freqüência f (Hz = Hertz), maior a taxa de variação da tensão e maior o
valor da corrente no capacitor
Para uma determinada variação da tensão nos terminais do capacitor
capacitor, quanto maior a
capacitância C (F = Farad),
Farad maior a corrente capacitiva resultante
IC é proporcional a ωC
• Corrente no capacitor
) *
)
Figura 6 - Resposta do capacitor a uma tensão senoidal
Como
) )
" # Então,
) *
)
*" # * % 90( *
• Para um capacitor
tor ou elementos puramente capacitivos, a corrente iC está adiantada de 90o
em relação à tensão vC
o
Ou vC está atrasada de 90o em relação a iC
Figura 7 – Corrente senoidal adiantada de 90o em relação à tensão para capacitor
capaci puro
4
• Reatância Capacitiva
$) o
o
+
,)
(ohms, Ω)
Definida pela Lei de Ohm
Reatância capacitiva é oposição à corrente, mas não dissipa energia elétrica → troca de
energia entre fonte e campo elétrico do capacitor
OBS: É possível determinar se um circuito com um ou mais dispositivos é predominantemente capacitivo
ou indutivo pela relação de fase entre a tensão e a corrente de entrada
Corrente adiantada em relação à tensão aplicada → circuito predominantemente capacitivo
Tensão adiantada em relação à corrente total → circuito predominantemente indutivo
Exercícios
• Ex01 – (Boylestad, exemplo 14.2, pg.411) A corrente em um resistor de 5Ω vale i(t)=40sen(377t+30o).
Determine a expressão senoidal para a tensão do resistor.
• Ex02 – (Boylestad, exemplo 14.4, pg.411) A expressão para a tensão em um indutor L=0,5 H é
v(t) = 100sen(20t). Qual é a expressão senoidal para a corrente?
• Ex03 - (Boylestad, exemplo 14.6, pg.412) A expressão para a corrente em um capacitor C=100μF é
i(t) = 40sen(500t+60o). Qual é a expressão senoidal para a tensão no capacitor?
• Ex04 - (Boylestad, exemplo 14.7, pg.412) Dados os pares de expressões para tensões e correntes,
determine se o dispositivo é um capacitor, indutor ou resistor e calcule os valores de C, L ou R,
respectivamente
a. v(t)=100sen(377t+40o) e i(t)=20sen(377t+40o)
b. v(t)=500sen(157t+30o) e i(t)= sen(157t+120o)
c. v(t)=1000sen(377t+10o) e i(t)=5sen(377t-80o)
Comportamento de indutores e capacitores em corrente contínua, baixa e alta frequência
• Para circuitos CC, a freqüência é zero e a reatância do indutor é dada por:
$ 2./! 2. 0
! 0 0
o Está justificada a substituição de indutores por curtos-circuitos em circuitos CC,
• Em altas frequências, XL ↑=2π(f↑)L tem valor muito elevado, e na prática, o indutor pode ser
considerado como um circuito aberto
$ ∞ Ω à 45 67 / ∞ 89
• O capacitor pode ser substituído por um circuito aberto em circuitos CC, pois f=0 Hz, e,
$) 1
1
∞0
2./* 2.0
*
5
• Em freqüências muito altas e capacitâncias finitas,
$) ; 1
= 0 Ω à 45 67 / ∞ 89
2./ <
*
o A reatância capacitiva é muito pequena e, na prática, o capacitor pode ser substituído por
um curto-circuito
• Até aqui, foi considerado que a resistência de um resistor é independente da freqüência
aplicada
o Componentes reais têm capacitâncias parasitas e indutâncias dos terminais que são
sensíveis ao valor da freqüência aplicada
o Geralmente, são valores desprezíveis que só são notados quando freqüência é superior a
alguns MHz
Figura 8 – Curvas de variação da resistência com a freqüência para resistores de carbono
Exercícios
• Ex01 – (Boylestad, exemplo 14.8, pg.415) Para que valor de freqüência a reatância de um indutor de 200
mH é igual à resistência de um resistor de 5 kΩ?
• Ex02 – (Boylestad, exemplo 14.9, pg.415) Em que freqüência um indutor de 5 mH terá a mesma
reatância de um capacitor de 0,1 μF?
• Ex03 – (Boylestad, prob. 5,, pg.438)
pg.4
As expressões a seguir representam a corrente em um resistor de
7kΩ. Qual a expressão senoidal para a tensão?
a.
0,03sen754t
b.
2x10-3sen(400t-120o)
c.
6x10-6cos(ωt-2o)
• Ex04 – (Boylestad, prob. 7,, pg.438)
pg.438) Determine a indutância de um indutor cuja reatância é:
a.
20Ω em f = 2 Hz
b.
1000Ω em f = 60 Hz
6
• Ex05 – (Boylestad, prob. 14, pg.439) Determine a capacitância de um capacitor cuja reatância é:
a.
250Ω em f = 60 Hz
b.
10Ω em f = 25 Hz
• Ex06 – (Boylestad, prob. 20, pg.439) No caso dos pares de expressões para tensão e corrente dados a
seguir, indique se o dispositivo envolvido é um capacitor, indutor ou resistor e os valores de C, L ou R:
a.
v = 550sen(377t + 40o) e i = 11sen(377t - 50o)
b.
v = 360sen(754t + 80o) e i = 4sen(754t + 170o)
c.
v = 10,5sen(ωt + 13o) e i = 1,5sen(ωt + 13o)
2. Impedância
Introdução
• (Pinheiro, 2003) – Dentre as características do cabeamento metálico, que devem ser observadas
na montagem de uma rede, as mais importantes são a resistência e a impedância. A resistência
representa a perda de energia que um sinal sofre ao trafegar por um meio metálico. Esta perda
limita a distância máxima permitida, pois a atenuação do sinal aumenta com distância até um
ponto que o receptor não consegue reconhecer o sinal de dados. A impedância é uma
característica complexa que envolve a resistência e a reatância e que só pode ser medida com
equipamentos apropriados. Em princípio, uma impedância alta ou baixa não causa problema,
mas um cabo deve ter uma impedância correta (casamento de impedâncias) para evitar perda
de sinal e interferências.
• Álgebra fasorial é utilizada para solução rápida de problemas envolvendo circuitos CA em série e
em paralelo
• Regras usadas em circuitos CC podem ser aplicadas em circuitos CA
Impedância e Diagrama Fasorial
• Elementos Resistivos – v e i estão em fase
7 o
Em forma fasorial (V = Vef =
),
√?
⟹ A /
⟹ C /
Como v e i estão em fase,
D A
C
/E
/E
/ − /0( Ω
7
E o termo ZR é chamado impedância do elemento resistivo e é medida em ohms.
o
o
ZR não é um fasor → é a representação de uma grandeza em álgebra complexa na forma polar
Impedância ZR de um resistor puro → número complexo com apenas parte real R (parte imaginária
= 0)
o
• Reatância Indutiva - v adiantada 90 em relação à i
o
Em forma fasorial (V = Vef =
7 = !
$
),
√?
= ± + 90( ⟹ A = / + 90(
= ± ⟹ C = /
A impedância (reatância) indutiva ZL é dada por,
D =
o
A
C
=
/EGHIJ
/E
= / + 90( − = !/90( = K! Ω
Impedância ZL de um indutor puro → número complexo com apenas parte imaginária positiva XL
(parte real = 0) e medida em ohms
• Reatância Capacitiva - i adiantada 90o em relação à v
o
Em forma fasorial (V = Vef =
7 =
$)
*
),
√?
= ± ⟹ A = /
= ± + 90( ⟹ C = / + 90(
A impedância (reatância) capacitiva ZC é dada por,
D) =
o
A
C
=
/E
/EGHIJ
+
,)
= / − − 90( =
/−90( = −
L
,)
Ω
Impedância ZC de um capacitor puro → número complexo com apenas parte imaginária negativa
XC (parte real = 0) e medida em ohms
• Diagrama de Impedâncias – Representação no plano complexo da resistência, reatância indutiva e
reatância capacitiva de um circuito
8
Figura 9 - Diagrama de Impedâncias
• Resistência sempre está na parte positiva do eixo dos reais
• Reatância indutiva sempre está na parte positiva do eixo dos imaginários
• Reatância capacitiva sempre está na parte negativa do eixo dos imaginários
o Combinação de elementos diferentes num circuito → impedância total cujo ângulo está
entre +90o e -90o
o Ângulo total = 0o → circuito resistivo
o Ângulo total > 0o → circuito indutivo
o Ângulo total < 0o → circuito capacitivo
Exercícios
• Ex01 – (O’Malley, problema resolvido 12.1, pg.379) Encontre a impedância total na forma polar de um
indutor de 0,5H em série com um resistor de 20
20Ω em:
a. 0 Hz
b. 10 Hz
c. 10 kHz
• Ex02 – (Boylestad,
Boylestad, exemplo 15.6, pg. 446) Usando a álgebra de números complexos, determine v sobre
um capacitor de 0,5 Ω submetido a uma corrente i =6sen(ωt-60o)
3. Circuitos CA em Série
• As propriedades gerais dos circuitos CA em série são as mesmas dos circuitos
circu
CC
• A impedância total de um sistema com dispositivos em série é a soma das impedâncias
individuais
MN MO % MP % MQ % R % MS
9
Figura 10 - Impedâncias em série
Exercícios
• Ex01 – (O’Malley, 12.2,, pg.379) Um resistor de 200 Ω, um indutor de 150 mH e um capacitor de 2 μF
estão em série. Encontra a impedância total na forma polar para f = 400Hz e desenhe o diagrama de
impedâncias.
• Ex02 - (O’Malley, 12.4, pg.381
81) Uma bobina energizada por 120V, 60 Hz, solicita
solicit uma corrente de 2 A que
está atrasada da tensão aplicada de 40o. Quais os valores de resistência e indutância da bobina?
• Ex03 – (Boylestad, 8, pg.484)) Dado um circuito RC em série (R=10Ω; XC=30Ω)) alimentado por uma fonte
CA E = 120V/20o , calcule:
a. Impedância total ZT na forma polar;
b. Construa o diagrama de impedâncias;
c. Determine a corrente total I e as tensões VR e VC em forma fasorial e em expressão senoidal (f = 60
Hz);
d. Verifique a validade da Lei de Kirchoff das Tensões ao longo da malha fechada
• Ex04 – (O’Malley, 12.54,, pg.410)
pg.41 Uma carga tem uma tensão de 240/75o V e uma corrente de 20/60
20/ o A a
uma freqüência de 60 Hz. Encontre os dois elementos do circuito série que podem ser a carga.
4. Divisão de Tensão
• Divisão de Tensão ou Regra para Divisor de Tensão para circuitos CA
• Mesma regra que em circuitos CC, considerando fasores de tensão ao invés de tensões e
impedâncias ao invés de resistências
• Para o circuito abaixo, ZT = Z1 + Z2 + Z3
+
V1
-
Z1
+
V2
-
Z2
+
VT
Z3
V3
-
+ D+
DT T
? D?
DT T
U DU
DT T
10
Exercícios
• Ex01 – (O’Malley, 12.23, pg.391) Use divisão de tensão para encontrar VR, VL e VC no circuito abaixo
• Ex02 – (O’Malley, 12.24,, pg.391)
pg.3
Use divisão de tensão para encontrar a tensão
tens V no circuito mostrado
abaixo
5. Circuitos CA em Paralelo
• As propriedades gerais dos circuitos CA em paralelo são as mesmas dos circuitos CC
• Usando-se
se a Lei de Kirchoff das Correntes (LKC), temos
CN CO % CP % CQ % R % CS
I1
IT
Z1
I2
Z2
I3
Z3
11
• A impedância total de um sistema com dispositivos em paralelo é a soma dos inversos das
impedâncias individuais, ou,
O
O
O
O
O
%
%
% R%
MN MO MP MQ
MS
6. Admitância
Introdução
• Admitância (símbolo Y, unidade Siemens S) é o inverso da impedância
V
1
X
D
• Admitância de um circuito CA corresponde à condutância de um circuito resistivo CC
• A admitância total de um sistema com dispositivos em paralelo é a soma das admitâncias
individuais
Y N YO % YP % YQ % R % YS
• Admitância é representada por uma parte real G, a condutância, e uma parte imaginária, B, a
susceptância
• Exemplo
V
1
1
1
%
%
0,001 F K0,0004 % K0,0001 0,001 F K0,
1000 K2500 FK1000
7. Divisão de Corrente
• Mesma regra que em circuitos CC, considerando fasores de corrente
rrente ao invés de correntes e
impedâncias ao invés de resistências
12
I1
IT
+ Z1
V+
VT T
I2
Z2
? V?
VT T
I3
Z3
U VU
VT T
• Quando o circuito tiver do
ois ramos paralelos com impedâncias Z1 e Z2, a equação do divisor de
corrente é
+ D?
D+ % D? T
Exercícios
• Ex01 – (O’Malley, 12.25,, pg.392)
pg.39 Encontre a corrente I no circuito abaixo
• Ex02 - (O’Malley, 12.34,, pg.397)
pg.39 Encontre o mais simples circuito para
ralelo que tenha a mesma
impedância em 400 Hz que a combinação série de um resistor de 300 Ω, um
u indutor de 0,25 H e um
capacitor de 1 µF
• Ex03 – (O’Malley, 12.83, pg.415) Quais os dois elementos de um circuito em paralelo
pa
que têm admitância
de 0,4/-50o S em 60 Hz?
• Ex04 – (O’Malley, 12.85, pg.4415) Três elementos de um circuito em paralelo têm admitância de 6,3/-40o
MS a uma freqüência de 2 kHz.
kH Se um deles é um indutor de 60 mH, quais são
o os outros dois elementos?
Fontes:
BOYLESTAD, R. L. – Introdução à Análise de Circuitos, 2004. 10ª edição. Ed. Prentice-Hall
Prentice
O’MALLEY, J. – Análise de Circuitos, 19947. 2ª Edição. Ed. McGraw
McGraw-Hill
PINHEIRO, J. M. S. – Guia Completo de Cabeamento de Redes, 2003. 7ª Tiragem. Ed. Elsevier
E
13