matemática

MATEMÁTICA
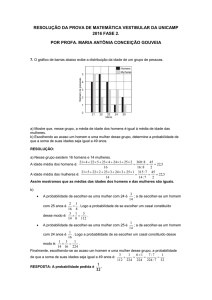
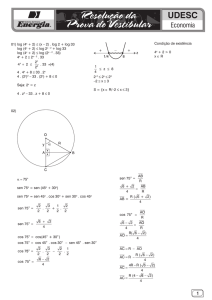
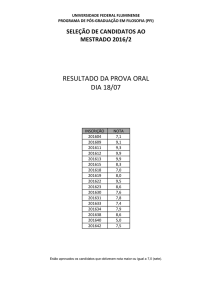
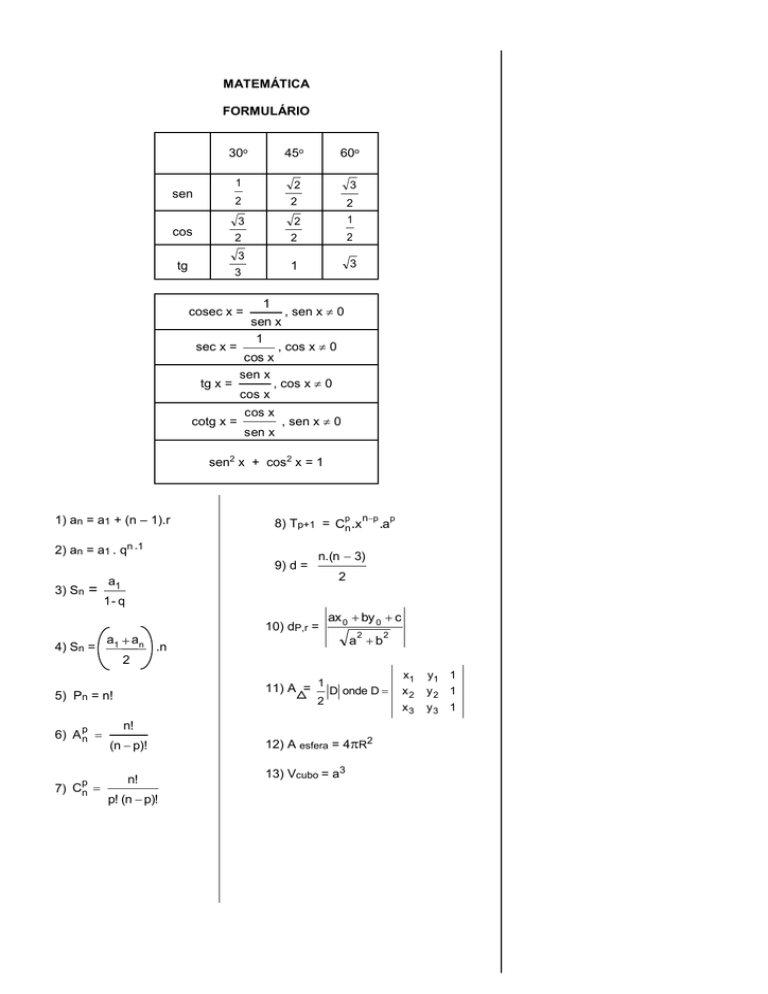
FORMULÁRIO
sen
cos
tg
30o
45o
1
2
3
2
2
3
2
2
1
2
2
2
1
3
3
3
60o
1
, sen x  0
sen x
1
sec x =
, cos x  0
cos x
sen x
tg x =
, cos x  0
cos x
cosec x =
cotg x =
cos x
sen x
, sen x  0
sen2 x + cos2 x = 1
1) an = a1 + (n – 1).r
p
8) Tp+1 = Cn .x
2) an = a1 . qn -1
9) d =
3) Sn
=
4) Sn =
n p
.ap
n.(n  3)
2
a1
1- q
a1  an
10) dP,r =
ax 0  by 0  c
.n
2
a b
2
2
11) A = 1 D onde D 
5) Pn = n!
p
6) A n 
7)
p
Cn

2
n!
(n  p)!
n!
p! (n  p)!
12) A esfera = 4R2
13) Vcubo = a3
x1
y1 1
x2
y2 1
x3
y3 1
INTRODUÇÃO
A análise a respeito da prova de Matemática do Concurso Vestibular-UFSC/2000 e de seus resultados, foi realizada por amostragem,
através da prova tipo 1/A.
25) Determine a soma dos números associados à(s) proposição(ões)
VERDADEIRA(S).
01. Os ângulos internos de um triângulo são proporcionais a 2, 3 e 4
respectivamente. A medida do maior deles é 80.
02. O perímetro de um paralelogramo de lados x e 2x é igual a 60 cm.
A medida de seus lados são 20 cm e 40 cm.
04. O polígono cujo número de diagonais é igual ao número de lados é o
pentágono.
08. A altura relativa à hipotenusa, de um triângulo retângulo de catetos
12 cm e 16 cm, mede 20 cm.
16. A medida de um ângulo inscrito, relativo a uma circunferência, é
metade da medida do arco correspondente.
Gabarito: 21 (01 + 04 + 16)
Número de acertos: 568 (7,39%)
Grau de dificuldade previsto: Fácil
Grau de dificuldade obtido: Difícil
SOLUÇÃO:
01. Verdadeira.

2


3

v
4

180   v

9
4
  v  80 
02. Falsa. x + x + 2x + 2x = 60 cm  x = 10 cm  As medidas de
seus lados são 10 cm e 20 cm.
04. Verdadeira. d = n 
gono.
n(n - 3)
= n  n(n – 5) = 0  n = 5  Pentá2
08. Falsa. b = 12 cm , c = 16 cm  a = 20 cm (hipotenusa)  h.a = b.c
 h.20 cm = 12 cm . 16 cm  h = 9,6 cm.
16. Verdadeira. Trata-se de um teorema da geometria plana que estabelece a relação entre ângulos e arcos da circunferência.
ANÁLISE DA QUESTÃO:
A questão envolve conhecimentos elementares de geometria
plana como: a soma das medidas dos ângulos internos de um triângulo;
o cálculo do perímetro e do número de diagonais de um polígono; relações métricas no triângulo retângulo e relação entre ângulos e arcos da
circunferência. Embora essa questão tenha grau de dificuldade fácil, os
resultados apontaram que ela se mostrou difícil para os candidatos.
Nessa questão, três pontos merecem ser destacados.
Primeiro, o fato de que as proposições corretas tiveram, separadamente, um bom número de preferências (01 – 41,22%; 04 – 64,52%;
16 – 40,57%), e que, o problema constitui-se na sua combinação, realizada por um número reduzido de candidatos. Nesse mesmo sentido,
deve-se destacar o fato de que 9,27% dos candidatos assinalaram a
resposta 05 (01 + 04), e outros 6,11%, a resposta 20 (04 + 16).
Segundo, o fato de que 49,06% dos candidatos consideraram a
proposição 08 como correta, fazendo com que as respostas 12 (04 + 08)
e 13 ( 01 + 04 + 08) tivessem 8,81% e 6,74% de preferência, respectivamente. É possível que esses candidatos não tenham prestado atenção
ao fato de que a proposição se referia à altura relativa à hipotenusa e
não, simplesmente, à hipotenusa, que realmente media 20 cm. Faltou a
esses candidatos lerem mais atentamente a proposição.
Terceiro, o fato de que apesar de 40,57% dos candidatos terem
considerado correta a proposição 16, ela fez parte de forma significativa
de apenas duas combinações 20 (04 + 16) – 6,11% e 21 (01 + 04 + 16) –
7,39%. Isso indica que essa proposição tenha sido talvez uma das responsáveis pelo baixo índice de acerto dos candidatos e que esse tópico
de geometria, trabalhado na 7a série do Ensino Fundamental, deva ser
melhor consolidado.
26) Um polinômio P(x) dividido por (x + 1) dá resto 3 e por (x – 2) dá
resto 6. O resto da divisão de P(x) pelo produto (x + 1).(x – 2) é da
forma ax + b, com a, b
é:
 .
O valor numérico da expressão a + b
Gabarito: 05 (Aberta)
Número de acertos: 719 (9,46%)
Grau de dificuldade previsto: Médio
Grau de dificuldade obtido: Difícil
SOLUÇÃO:
Pelo teorema do resto, temos: P(-1) = 3 e P(2) = 6.
Sejam Q(x) e R = ax + b, respectivamente, o quociente e o resto
da divisão de P(x) por (x + 1).(x - 2); temos:
P(x) = Q(x).(x + 1).(x - 2) + (ax + b).
Tomemos os valores numéricos desses polinômios em -1 e 2:
P(-1) = Q(-1).(-1 + 1).(-1 - 2) + (-a + b)  3 = -a + b
P(2) = Q(2).(2 + 1).(2 - 2) + (2a + b)
 6 = 2a + b
Resolvendo o sistema formado por -a + b = 3 e 2a + b = 6,
resulta a = 1 e b = 4.
Logo, o valor numérico da expressão a + b = 5.
}
ANÁLISE DA QUESTÃO:
Questão aberta, envolvendo divisão de polinômios. Nessa questão, 6,25% dos candidatos assinalaram a resposta 03 e 15,12%, a
resposta 09. Outros 7,83% dos candidatos optaram pela resposta 18.
Embora o índice de concentração nessas respostas incorretas não seja
muito significativo, a análise sugere que os candidatos, por terem dificuldades no estudo de polinômios, tenham simplesmente combinado os
dados do enunciado da questão, de forma a dar uma resposta (03;
03 + 06 = 09; 03.06 = 18).
Considerando-se que esse assunto é muito explorado no Ensino
Médio e em vestibulares, o resultado ficou aquém do esperado.
27) Determine a soma dos números associados à(s) proposição(ões)
VERDADEIRA(S).
01. A medida em radianos de um arco de 225 é
11

rad.
6
02. A menor determinação positiva de um arco de 1000 é 280.
04. Os valores de m, de modo que a expressão sen x = 2m – 5 exista,
estão no intervalo [2,3].
08. sen x  cos x para
16. Se tg x =
3
e
4
a



4
x
x 

.
4
 , então o valor de sen x – cos x é igual
3
2
1
.
5
32. Se sen x  0, então cosec x  0.
64. A solução da equação 2sen2x + 3sen x = 2 para 0  x  2
5
x=
ou x =
.
6
6
é


Gabarito: 86 (02 + 04 + 16 + 64)
Número de acertos: 425 (5,54%)
Grau de dificuldade previsto: Difícil
Grau de dificuldade obtido: Difícil
SOLUÇÃO:
01. Falsa. x =
225   πrad
180 
x=
5πrad
4
02. Verdadeira. 1000o = 2.360o + 280o.
04. Verdadeira. -1  2m - 5  1  4  2m  6  2  m  3  m  [2, 3].
08. Falsa. Basta tomar x = 0  sen 0 > cos 0  0 > 1. Absurdo.
3

4
sen x 3
3cos x
  sen x =
.
cos x 4
4
4
3
tuindo em sen2 x + cos2 x = 1  cos x =
 sen x = .
5
5
1
3
(-4)
Logo, sen x – cos x = - –
= .
5
5
5
16. Verdadeira. tg x =
1
32. Falsa. Como cosec x =
sen x
cosec x > 0.
, sen x  0
 Se sen x > 0 
64. Verdadeira. Faça: y = sen x  2y2 + 3y = 2 
1
1

5

 sen x 
x
ou x 
y1 
2
2
6
6

y 2   2 (absurdo)

Substi-
ANÁLISE DA QUESTÃO:
A questão envolve conhecimentos básicos e fundamentais de trigonometria. Nessa questão, todas as proposições corretas tiveram,
separadamente, um bom índice de preferências (02 – 50,13%; 04 –
54,03%; 16 – 30,79%; 64 = 35,32%). O problema foi a combinação de
ambas, realizada por um número reduzido de candidatos. Um exemplo
disso é o fato de que 6,73% dos candidatos assinalaram a proposição 06
(02 + 04) e 6,43%, a proposição 70 (02 + 04 + 64).
Outro ponto que merece ser destacado nessa análise é o fato de
que 33,28% dos candidatos consideraram a proposição 32 como correta.
É possível que esses candidatos não tenham dado a devida atenção à
1
, sen x  0 , fornecida no formusen x
lário da prova, a qual lhes possibilitaria perceber que o sinal da cosec x é
igual ao sinal do sen x.
A partir dessa e de outras análises de questões, envolvendo trigonometria, apresentadas em relatórios de anos anteriores, pode-se dizer que esse tópico é bem trabalhado no Ensino Médio. Porém, é necessário que esse conhecimento seja melhor consolidado, principalmente no
que se refere à aplicação das relações fundamentais e derivadas entre os
números trigonométricos de um mesmo arco, já que 6,73% dos candidatos consideraram como corretas somente as proposições 02 e 04 e
outros, 6,43%, apenas as proposições 02, 04 e 64. Isso indica que a
proposição 16 foi, talvez, a responsável pelo baixo índice de acerto dos
candidatos.
relação fundamental cosec x =
28) De acordo com o gráfico abaixo, assinale a(s) proposição(ões)
VERDADEIRA(S).
y
3
1
2
0

1
x
s
r
01. A equação da reta s é 3x – 2y + 6 = 0.
02. A reta s e a reta r são perpendiculares.
04. As retas r e s se interceptam no ponto de abscissa
4
.
5
08. A distância da origem do sistema de coordenadas cartesianas à reta
r é de
2
unidades.
2
16. A área da região do plano limitada pelas retas r, s e pelo eixo das
3
abscissas é igual a
unidades de área.
10
Gabarito: 09 (01 + 08)
Número de acertos: 1.164 (15,20%)
Grau de dificuldade previsto: Médio
Grau de dificuldade obtido: Difícil
SOLUÇÃO:
01. Verdadeira.
x y 1
-2 0 1 = 0
0 3 1

3x – 2y + 6 = 0
x y 1
02. Falsa. 0
1
1 1 =0
0 1
 x+y –1 =0
 mr = -1
3
s: 3x – 2y + 6 = 0  ms =
2
1
mr   r e s não são perpendiculares.
ms
r: x + y – 1 = 0
04. Falsa. Resolvendo o sistema formado por
4
9
3x – 2y + 6 = 0, resulta x = e y= .
5
5
08. Verdadeira. dP,r =
1(0)  1(0)  1
1 1
2
2
 dP,r = -
1
2
x+y–1=0
 dP,r =
e
2
uni2
dades.
1
1
A =
-2
2 4
5
27
A =
unidades de área.
10
1
16. Falsa. A = D 
2
0 1
1 27
0 1  A =
5
2
9 1
5

ANÁLISE DA QUESTÃO:
Nessa questão, são abordados os conhecimentos básicos e fundamentais de geometria analítica.
A partir da análise do quadro de respostas, constata-se um bom
índice de preferência pelas proposições corretas (01 – 39,59%; 08 –
44,63%), mas, apenas 15,20% dos candidatos optaram pelas duas, simultaneamente, isto é, obtiveram a resposta correta.
Merece destaque o fato de um número significativo de candidatos
(47,32%) considerarem a proposição 02 como correta, fazendo com que
as respostas 02 (02); 10 (02 + 08) e 18 (02 + 16) tivessem 13,71%,
6,80% e 7,39% de preferências, respectivamente. É possível que esses
candidatos tenham sido induzidos pela representação gráfica apresentada na questão, não verificando, portanto, a condição de perpendicularismo das retas r e s.
29) Determine a soma dos números associados à(s) proposição(ões)
VERDADEIRA(S).
log 32 é igual a –
01. O valor do
5
.
2
0,25
a
02. Se a, b e c são números reais positivos e x =
b
1
log x = 3log a – 2log b –
3
2
, então
c
log c.
2
04. Se a, b e c são números reais positivos com a e c diferentes de
log b
c
.
um, então tem-se log b 
a
log a
c
08. O valor de x que satisfaz à equação 4x – 2x = 56 é x = 3.
2
16.
2,3
>
3
2
1,7
3
Gabarito: 31 (01 + 02 + 04 + 08 + 16)
Número de acertos: 511 (6,66%)
Grau de dificuldade previsto: Fácil
Grau de dificuldade obtido: Difícil
SOLUÇÃO:
x
32 = x   25    1 
01. Verdadeira. log0,25
2
100
x =–

5
.
2
 a3
02. Verdadeira. log x = log 
 b2 c



x
2 
= 25  2-2x = 25 

 . Pelas propriedades dos logaritmos




temos: log x = log a3 – log b 2 c  log x = 3 log a – log b2  log c

log x = 3 log a – (2 log b + log c½)  log x = 3 log a –
1
1
(2 log b + log c)  log x = 3 log a – 2 log b –
log c.
2
2
04. Verdadeira. Trata-se da propriedade da mudança de base de logaritmos.
08. Verdadeira. 4x – 2x = 56  22x – 2x = 56. Faça: y = 2x 
y2 – y – 56 = 0  y1 = -7
y2 = 8
16. Verdadeira.
2
3
2,3
>
 2x = -7 (absurdo)
 2x = 8  x = 3.
2
3
1,7
3
  
2
1, 7
2,3
>
3
 
2
.

ANÁLISE DA QUESTÃO:
A questão envolve conhecimentos básicos de logaritmos e exponenciais.
Embora prevista como fácil, o resultado mostrou que a questão
representou ser difícil para os candidatos.
Acredita-se que essa
dificuldade não se deve, propriamente, ao conteúdo em questão, mas à
combinação das proposições corretas. A análise do quadro de respostas
confirma isso, demonstrando um bom índice de preferência pelas
proposições corretas, separadamente, (01 – 40,76%; 02 – 52,05%; 04 –
60,90%; 08 – 71,68%; 16 – 33,46%), mas que apenas 6,66% dos
candidatos foram capazes de combiná-las corretamente. Esse fato pode
também ser evidenciado pelos índices de preferência das respostas que
são combinações parciais dessas proposições, como 06 (02+04 – 4,91%);
08 (08 – 9,16%); 10 (02 + 08 – 6,95%); 12 (04 + 08 – 7,98%); 13 (01 + 04
+ 08 – 5,13%); 14 (02 + 04 + 08 – 8,08%) e 15 (01 + 02 + 04 + 08 – 6%).
Deve-se destacar ainda, que apesar de 40,76% dos candidatos
terem considerado correta a proposição 01 e 33,46%, a proposição 16,
essas proposições fizeram parte, de forma significativa, de apenas três
(3) combinações: 13 (01 + 04 + 08 – 5,13%); 15 (01 + 02 + 04 + 08 –
6%) e 31 (01 + 02 + 04 + 08 + 16 – 6,66%). Isso indica que essas
proposições tenham sido, talvez, as responsáveis pelo baixo índice de
acerto dos candidatos e que os tópicos logaritmos e exponenciais devem
ser melhor explorados no Ensino Médio.
30) Determine a soma dos números associados à(s) proposição(ões)
VERDADEIRA(S).
4
A6
01. Simplificando
3
obtemos 6.
A5
02. Podemos formar 720 anagramas com ou sem significado com as
letras da palavra ESCOLA.
04. Numa sala estão 5 professores e 6 alunos. O número de grupos
que podemos formar, tendo 2 professores e 3 alunos, é 30.
08. Se
3
x -2
A x  10C x
 0 , então x é igual a 7.
16. O termo independente de x no desenvolvimento (3x – 2)4 é 16.
Gabarito: 27 (01 + 02 + 08 + 16)
Número de acertos: 629 (8,20%)
Grau de dificuldade previsto: Médio
Grau de dificuldade obtido: Difícil
SOLUÇÃO:
ANÁLISE DA QUESTÃO:
A questão aborda conhecimentos básicos e fundamentais de
análise combinatória. Nessa questão, todas as proposições corretas tiveram, separadamente, um bom índice de preferências (01 – 51,11%; 02 –
77,23%; 08 – 35,56%; 16 – 47,10%). O problema foi a combinação de
ambas, realizada por apenas 8,20% dos candidatos.
A análise do quadro de respostas (02 – 7,62%); 03 (01 + 02 –
9,52%); 11 (01 + 02 + 08 – 7,84%); 18 (02 + 16 – 7,99%); 19 (01 + 02 +
16 – 7,37%) sugere que os candidatos têm um bom conhecimento de
análise combinatória, mas é necessário que esse tópico seja melhor
explorado no Ensino Médio.
31) Determine a soma dos números associados à(s) proposição(ões)
VERDADEIRA(S).
01. A razão da P.A. em que a1 =  8 e a20 = 30 é r = 2.
02. A soma dos termos da P.A. (5, 8, ..., 41) é 299.
04. O primeiro termo da P.G. em que a3 = 3 e a7 =
5 5
5 , , ,...
2 4
08. A soma dos termos da P.G.
3
é 12.
16
é 10.
Gabarito: 15 (01 + 02 + 04 + 08)
Número de acertos: 1.501 (19,58%)
Grau de dificuldade previsto: Fácil
Grau de dificuldade obtido: Difícil
SOLUÇÃO:
01. Verdadeira. a1 = -8 ,
an = a1 + (n – 1).r
a20 = 30

30 = -8 + 19r
 r=
38
= 2.
19
02. Verdadeira. a1 = 5; r = 3; an = 41; n = 13
a1  a n
Sn =
2
.n
 Sn =
04. Verdadeira. a3 = 3 , a7 =
q4 =
 a7 = a3 q4 
1
1
 q= .
16
2
a3 = a1 q2  3 = a1.
1
4
08. Verdadeira. a1 = 5 , q =
Sn =
3
16
(5  41)
 13 = 299
2
a1
1- q
 Sn =
 a1 = 12.
1
2
5
= 10.
1
2
3
= 3q4
16

ANÁLISE DA QUESTÃO:
Essa questão, em princípio, pode ser julgada fácil, pois envolve
apenas aplicação direta de fórmulas de P.A. e P.G.
Observa-se que 72,94% dos candidatos optaram pela proposição
01; 65,61% pela proposição 02; 59,20% pela proposição 08 e 48,34%
pela proposição 04.
O fato de que 19,58% dos candidatos optaram pela resposta
11 (01 + 02 + 08) e 11,39% pela resposta 03 (01 + 02), indica que a
proposição 04 foi, talvez, responsável pelo baixo índice de acerto na
questão, pois os candidatos tinham que encontrar, primeiro, a razão da
P.G., para depois, o primeiro termo. Para encontrar a razão não havia
uma fórmula pronta.
32) Considere o sistema S1:
x + 3y = 0
2x – 6y = 0 e determine a soma dos
números associados à(s) proposição(ões) VERDADEIRA(S).
01. O par ordenado (15,5) é uma solução do sistema S1.
02. O sistema S1 é possível e determinado.
04. A solução do sistema S1 é uma reta que não passa pela origem.
08. O sistema S2:
2x + 6y = 0
10x – 30y = 0 é equivalente ao sistema S1.
Gabarito: 09 (01 + 08)
Número de acertos: 1.660 (21,64%)
Grau de dificuldade previsto: Médio
Grau de dificuldade obtido: Difícil
SOLUÇÃO:
01. Verdadeira. Substituindo x por -15 e y por 5, no sistema S1, verifica-se que o par (-15 , 5) é uma solução de S1.
- 15  15  0

 30  30  0
02. Falsa.
 x  3y  0

- 2x  6y  0
Como  = x = y = 0, tem-se que o sistema é possível e indeterminado.
04. Falsa. De S1 segue que x = -3y.
O conjunto solução de S1 é o conjunto dos pares (x, y) que pertencem à reta x = -3y.
O par (0, 0) é uma solução do sistema.
08. Verdadeira. A solução de S2 é o conjunto dos pares (x, y), tais que
x = -3y. Logo, S1 e S2 têm o mesmo conjunto solução.
ANÁLISE DA QUESTÃO:
A questão, que envolve análise de sistemas de equações lineares, obteve apenas 21,44% de acerto.
Dentre todas as proposições, a de número 08 teve o maior índice
de acerto, 74,84%.
43,33% dos candidatos indicaram a proposição 02 (falsa), como
correta. Nessa questão não se lembraram das condições para que um
sistema seja possível e determinado.
Apenas 49,71% optaram pela proposição 01, considerada a mais
fácil.
Conclui-se que a maioria dos candidatos, talvez, saiba resolver
sistemas, mas não analisar as soluções do sistema e o próprio sistema.
x 1
definida para todo x real e x  1 e
x 1
g(x) = 2x + 3 definida para todo x real.
Determine a soma dos números associados à(s) proposição(ões)
VERDADEIRA(S).
33) Sejam as funções f(x) =
01.
.
02. O domínio da função fg (f composta com g) é
4
04. O valor de g(f(2)) é igual a
.
3
1
08. A função inversa da g é definida por g (x) 
x3
.
2
16. A reta que representa a função g intercepta o eixo das abscissas
em

3
,0 .
2
32. A função f assume valores estritamente positivos para x  – 1
ou x  1.
Gabarito: 59 (01 + 02 + 08 +16 + 32)
Número de acertos: 191 (2,49%)
Grau de dificuldade previsto: Médio
Grau de dificuldade obtido: Difícil
SOLUÇÃO:
01. Verdadeira. f(x) =
x 1
x 1

x 
f 1
1 1
= x
1 1
x
=
1x
x
1 x
x
=
1 x
=
1 x
1  x 
 = – f(x).
 x  1
– 
02. Verdadeira. fg(x) = f(g(x)) = f (2x + 3) =
Portanto,
04. Falsa. g(f(2)) = g(3) = 9.
2x  4
x2
2x  3  1
=
=
.
2x  3  1
2x  2
x 1
 y = 2x + 3
08. Verdadeira. g(x) = 2x + 3
1
Portanto, g (x) 
x3
2
 x =
y 3
.
2
.
16. Verdadeira. O gráfico da função g(x) é uma reta definida por
y = 2x + 3.
Fazendo y = 0, tem-se 2x + 3 = 0, ou seja, x = -
3
.
2
Portanto, a reta que representa a função g(x) intercepta o eixo das
abscissas no ponto 
3
,0 .
2
32. Verdadeira. f(x) =
x+1<0
e
x 1
x 1
x – 1 < 0.
Logo, f(x) > 0
> 0 para x + 1 > 0 e x – 1 > 0 ou
para x < -1
ou
x > 1.
ANÁLISE DA QUESTÃO:
Essa questão apresenta um baixo índice de acertos (2,49%),
tratando-se de um assunto bastante explorado no Ensino Médio.
Analisando o número de acertos nas proposições corretas, observa-se que os candidatos tiveram dificuldades em efetuar a composição
de funções (proposição 02 – 34,25% e 04 – 21,08% de acerto), e em

determinar a expressão para f 1x
(proposição 01 – 30,78%).
34) O gráfico abaixo representa temperatura T(C) x tempo t (h).
T(C)
30
25
20
15
10
5
t (h)
1
2
3
4
5
6
01. No intervalo entre t1 = 1 e t2 = 2 a temperatura diminuiu numa
taxa constante.
02. A função que determina a temperatura entre t1 = 5 e t2 = 6 é do
tipo y = ax + b, com a  0.
04. A temperatura diminuiu mais rapidamente no intervalo entre t 1 = 1
e t2 = 2 do que no intervalo entre t2 = 2 e t3 = 3.
08. A temperatura máxima ocorreu no instante t = 2.
16. A temperatura mínima ocorreu no instante t = 3.
Gabarito: 17 (01 + 16)
Número de acertos: 2.944 (38,39%)
Grau de dificuldade previsto: Médio
Grau de dificuldade obtido: Médio
SOLUÇÃO:
01. Verdadeira. No intervalo t1 = 1 e t2 = 2, a temperatura está representada, geometricamente, por um segmento de reta decrescente. O
coeficiente angular da reta é o mesmo em qualquer ponto da reta. A
taxa de variação é o coeficiente angular da reta.
Portanto, a temperatura diminui a uma taxa constante nesse
intervalo.
02. Falsa. A função que determina a temperatura no intervalo [5, 6] é do
tipo y = ax + b com a > 0.
04. Falsa. No intervalo entre t1 = 1 e t2 = 2, a temperatura diminuiu 5 oC
(de 20 oC para 15 oC); no intervalo entre t2 = 2 e t3 = 3, a temperatura diminuiu 17,5 oC (de 22,5 oC para 5 oC).
08. Falsa. A temperatura máxima ocorreu no instante t = 6.
16. Verdadeira. A temperatura mínima ocorreu no instante t = 3.
ANÁLISE DA QUESTÃO:
Essa questão que trata de análise de gráficos teve um índice
médio de acerto (38,39%).
Cada uma das proposições corretas, separadamente, teve um
alto número de preferências ( 01 – 70,96% e 16 – 90,28%). O problema
foi a combinação delas.
11,78% dos candidatos optaram pela resposta 19 (01 + 02 + 16).
A proposição 02 teve 26,71% de preferência, motivo este que,
talvez tenha sido responsável pelo baixo índice de acerto na questão, ao
assinalarem a proposição 02 como correta, não levando em consideração
a restrição sobre o coeficiente a.
35) O volume, em cm 3, de um cubo circunscrito a uma esfera de
16 cm2 de superfície é:

Gabarito: 64 (Aberta)
Número de acertos: 2.700 (35,51%)
Grau de dificuldade previsto: Difícil
Grau de dificuldade obtido: Médio
SOLUÇÃO:
A – área (esfera) = 16
V – Volume (cubo) = 3
A = 4r2 = 16  r = 2
Se um cubo está circunscrito a uma esfera de raio r, então a aresta do
cubo é  = 2r.
 = 2.2 = 4
V = 43 = 64.
ANÁLISE DA QUESTÃO:
A questão do tipo aberta envolve aplicação de fórmulas da geometria espacial.
35,51% dos candidatos acertaram a questão e 15,91% deram a
resposta 08, pois usaram a medida do raio da esfera como a aresta do
cubo.
36) Dois pescadores P1 e P2 estão na beira de um rio de margens
paralelas e conseguem ver um bote B na outra margem. Sabendo
^1P2 =  e BP^ P =  e que
que P1 P2 = 63 m, os ângulos BP
2 1
tg  = 2 e tg  = 4, a distância entre as margens (em metros) é:
Gabarito: 84 (Aberta)
Número de acertos: 797 (10,52%)
Grau de dificuldade previsto: Médio
Grau de dificuldade obtido: Difícil
63 – a
P1
SOLUÇÃO:

a
P2

x
x
= 2
63  a
x
x
tg  =
= 4  a=
a
4
B
x
4x
=2 
= 2  504 – 2x = 4x  6x = 504 
252  x
63  x
4
tg  =
x = 84.
ANÁLISE DA QUESTÃO:
A questão envolve conceitos de trigonometria. Observa-se que,
10,52% dos candidatos responderam corretamente a questão, e 7,90%
deram a resposta 63, que é a distância dada no problema, entre os dois
pescadores, e não a distância entre as margens do rio.
Para esses candidatos faltou interpretar e representar geometricamente o problema. Os demais candidatos conseguiram outras respostas nada significativas.
CONCLUSÃO
A prova procurou contemplar todo o programa, através de questões simples, com nível de dificuldade médio, priorizando a inclusão de
um maior número de questões do tipo de proposições de múltipla escolha, com o objetivo de valorizar os acertos parciais dos candidatos.
Acredita-se que os desempenho entre o grau de dificuldade previsto e os resultados obtidos deve-se à referida inclusão, já que esse tipo
de questão mostrou-se mais difícil para os candidatos.
Finalmente, percebe-se a necessidade de que os conteúdos de
Matemática sejam mais explorados no Ensino Fundamental e no Ensino
Médio, dando-se especial atenção aos seus fundamentos e aplicações.