Lista de Gráficos Cinemática – Professor Franklyn Laporte

Lista de Gráficos Cinemática – Professor Franklyn Laporte
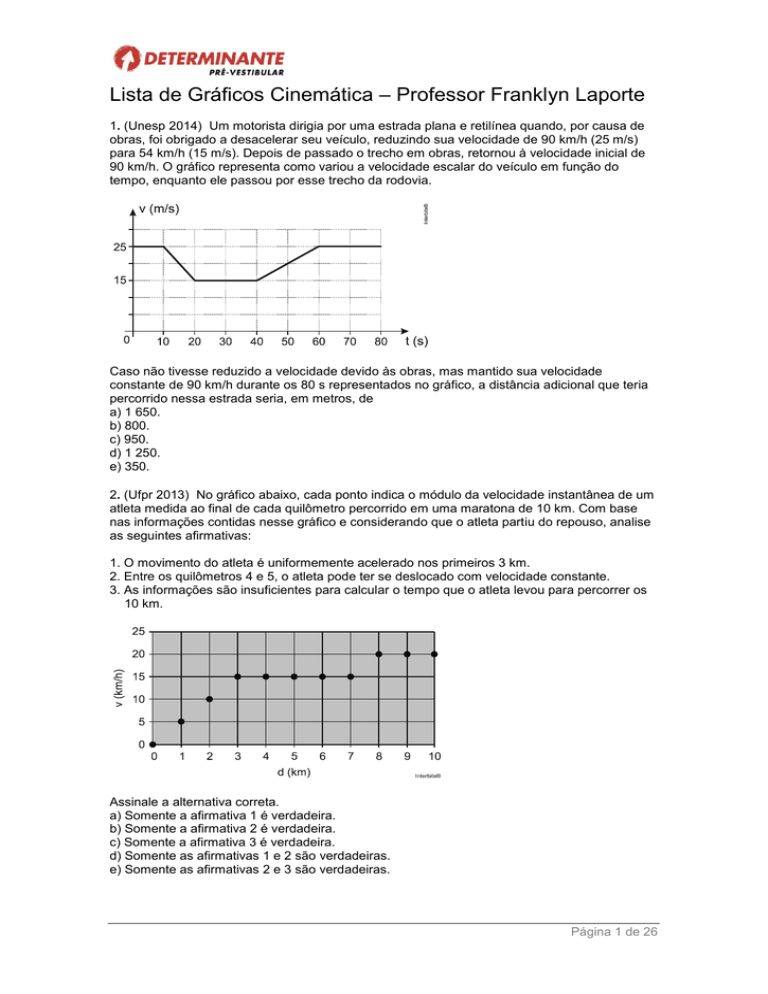
1. (Unesp 2014) Um motorista dirigia por uma estrada plana e retilínea quando, por causa de
obras, foi obrigado a desacelerar seu veículo, reduzindo sua velocidade de 90 km/h (25 m/s)
para 54 km/h (15 m/s). Depois de passado o trecho em obras, retornou à velocidade inicial de
90 km/h. O gráfico representa como variou a velocidade escalar do veículo em função do
tempo, enquanto ele passou por esse trecho da rodovia.
Caso não tivesse reduzido a velocidade devido às obras, mas mantido sua velocidade
constante de 90 km/h durante os 80 s representados no gráfico, a distância adicional que teria
percorrido nessa estrada seria, em metros, de
a) 1 650.
b) 800.
c) 950.
d) 1 250.
e) 350.
2. (Ufpr 2013) No gráfico abaixo, cada ponto indica o módulo da velocidade instantânea de um
atleta medida ao final de cada quilômetro percorrido em uma maratona de 10 km. Com base
nas informações contidas nesse gráfico e considerando que o atleta partiu do repouso, analise
as seguintes afirmativas:
1. O movimento do atleta é uniformemente acelerado nos primeiros 3 km.
2. Entre os quilômetros 4 e 5, o atleta pode ter se deslocado com velocidade constante.
3. As informações são insuficientes para calcular o tempo que o atleta levou para percorrer os
10 km.
Assinale a alternativa correta.
a) Somente a afirmativa 1 é verdadeira.
b) Somente a afirmativa 2 é verdadeira.
c) Somente a afirmativa 3 é verdadeira.
d) Somente as afirmativas 1 e 2 são verdadeiras.
e) Somente as afirmativas 2 e 3 são verdadeiras.
Página 1 de 26
3. (Fatec 2013) O jipe-robô Curiosity da NASA chegou a Marte, em agosto de 2012,
carregando consigo câmeras de alta resolução e um sofisticado laboratório de análises
químicas para uma rotina de testes. Da Terra, uma equipe de técnicos comandava seus
movimentos e lhe enviava as tarefas que deveria realizar.
Imagine que, ao verem a imagem de uma rocha muito peculiar, os técnicos da NASA, no
desejo de que o Curiosity a analisasse, determinam uma trajetória reta que une o ponto de
observação até a rocha e instruem o robô para iniciar seu deslocamento, que teve duração de
uma hora.
Nesse intervalo de tempo, o Curiosity desenvolveu as velocidades indicadas no gráfico.
O deslocamento total realizado pelo Curiosity do ponto de observação ao seu destino foi, em
metros,
a) 9.
b) 6.
c) 4.
d) 2.
e) 1.
4. (Fgv 2013) Um carro deslocou-se por uma trajetória retilínea e o gráfico qualitativo de sua
velocidade (v), em função do tempo (t), está representado na figura.
Analisando o gráfico, conclui-se corretamente que
a) o carro deslocou-se em movimento uniforme nos trechos I e III, permanecendo em repouso
no trecho II.
b) o carro deslocou-se em movimento uniformemente variado nos trechos I e III, e em
movimento uniforme no trecho II.
c) o deslocamento do carro ocorreu com aceleração variável nos trechos I e III, permanecendo
constante no trecho II.
d) a aceleração do carro aumentou no trecho I, permaneceu constante no trecho II e diminuiu
no trecho III.
e) o movimento do carro foi progressivo e acelerado no trecho I, progressivo e uniforme no
trecho II, mas foi retrógrado e retardado no trecho III.
5. (G1 - ifpe 2012) Toda manhã, um ciclista com sua bicicleta pedala na orla de Boa Viagem
durante 2 horas. Curioso para saber sua velocidade média, ele esboçou o gráfico velocidade
escalar em função do tempo, conforme a figura abaixo. A velocidade média, em km/h, entre o
intervalo de tempo de 0 a 2 h, vale:
Página 2 de 26
a) 3
b) 4
c) 6
d) 8
e) 9
6. (G1 - cftmg 2012) Um corpo tem seu movimento representado pelo gráfico abaixo.
Ao final de duas horas de movimento, seu deslocamento, em km, será igual a
a) 0.
b) 20.
c) 40.
d) 80.
7. (Espcex (Aman) 2012) O gráfico abaixo representa a velocidade(v) de uma partícula que se
desloca sobre uma reta em função do tempo(t). O deslocamento da partícula, no intervalo de
0 s a 8 s, foi de:
a) –32 m
b) –16 m
c) 0 m
d) 16 m
e) 32 m
Página 3 de 26
8. (Epcar (Afa) 2012) Um bloco se movimenta retilineamente, do ponto A até o ponto C,
conforme figura abaixo.
Sua velocidade v em função do tempo t, ao longo da trajetória, é descrita pelo diagrama v x t
mostrado abaixo.
Considerando que o bloco passa pelos pontos A e B nos instantes 0 e t1, respectivamente, e
para no ponto C no instante t 2 , a razão entre as distâncias percorridas pelo bloco nos trechos
BC e AB, vale
t  t1
a) 2
t1
b)
 t2  t1 2
t 22
t t
c) 2 1
2  t1
t  t1
d) 2
2  t2
9. (Enem 2012) Para melhorar a mobilidade urbana na rede metroviária é necessário
minimizar o tempo entre estações. Para isso a administração do metrô de uma grande cidade
adotou o seguinte procedimento entre duas estações: a locomotiva parte do repouso em
aceleração constante por um terço do tempo de percurso, mantém a velocidade constante por
outro terço e reduz sua velocidade com desaceleração constante no trecho final, até parar.
Qual é o gráfico de posição (eixo vertical) em função do tempo (eixo horizontal) que representa
o movimento desse trem?
a)
b)
Página 4 de 26
c)
d)
e)
10. (Uff 2012) Policiais rodoviários são avisados de que um carro B vem trafegando em alta
velocidade numa estrada. No instante t 0 em que o carro B passa, os policiais saem em sua
perseguição. A figura ilustra as velocidades do carro B e do carro dos policiais (P) em função
do tempo.
Assinale a alternativa que especifica o instante de tempo em que o carro P alcança o carro B.
a) t1
b) t 2
c) t 3
d) t 4
e) t 5
11. (Espcex (Aman) 2011) O gráfico abaixo indica a posição (S) em função do tempo (t) para
um automóvel em movimento num trecho horizontal e retilíneo de uma rodovia.
Página 5 de 26
Da análise do gráfico, pode-se afirmar que o automóvel
a) está em repouso, no instante 1 min.
b) possui velocidade escalar nula, entre os instantes 3 min e 8 min.
c) sofreu deslocamento de 4 km, entre os instantes 0 min e 3 min.
d) descreve movimento progressivo, entre os instantes 1 min e 10 min.
e) tem a sua posição inicial coincidente com a origem da trajetória.
12. (Eewb 2011) O gráfico abaixo representa a velocidade em função do tempo de um objeto
em movimento retilíneo. Calcule a velocidade média entre os instantes t = 0 e t = 5h.
a) 5,0 m/s
b) 5,5 m/s
c) 6,0 m/s
d) 6,5 m/s
13. (Enem 2ª aplicação 2010) Rua da Passagem
Os automóveis atrapalham o trânsito.
Gentileza é fundamental.
Não adianta esquentar a cabeça.
Menos peso do pé no pedal.
O trecho da música, de Lenine e Arnaldo Antunes (1999), ilustra a preocupação com o trânsito
nas cidades, motivo de uma campanha publicitária de uma seguradora brasileira. Considere
dois automóveis, A e B, respectivamente conduzidos por um motorista imprudente e por um
motorista consciente e adepto da campanha citada. Ambos se encontram lado a lado no
instante inicial t = 0 s, quando avistam um semáforo amarelo (que indica atenção, parada
obrigatória ao se tornar vermelho). O movimento de A e B pode ser analisado por meio do
gráfico, que representa a velocidade de cada automóvel em função do tempo.
Página 6 de 26
As velocidades dos veículos variam com o tempo em dois intervalos: (I) entre os instantes 10s
e 20s; (II) entre os instantes 30s e 40s. De acordo com o gráfico, quais são os módulos das
taxas de variação da velocidade do veículo conduzido pelo motorista imprudente, em m/s 2, nos
intervalos (I) e (II), respectivamente?
a) 1,0 e 3,0
b) 2,0 e 1,0
c) 2,0 e 1,5
d) 2,0 e 3,0
e) 10,0 e 30,0
14. (Ufmg 2010) Ângela e Tânia iniciam, juntas, um passeio de bicicleta em torno de uma
lagoa.
Neste gráfico, está registrada a distância que cada uma delas percorre, em função do tempo:
Após 30 minutos do início do percurso, Tânia avisa a Ângela, por telefone, que acaba de
passar pela igreja.
Com base nessas informações, são feitas duas observações:
I - Ângela passa pela igreja 10 minutos após o telefonema de Tânia.
II - Quando Ângela passa pela igreja, Tânia está 4 km à sua frente.
Considerando-se a situação descrita, é CORRETO afirmar que
a) apenas a observa‫חד‬o I est‫ ב‬certa.
b) apenas a observação II está certa.
c) ambas as observações estão certas.
d) nenhuma das duas observações está certa.
15. (Ufla 2010) Quatro corpos 1, 2, 3 e 4 movem-se em uma trajetória retilínea e o diagrama
Página 7 de 26
velocidade versus tempo de cada um deles é mostrado a seguir. Considerando que todos os
corpos partiram do mesmo ponto, é CORRETO afirmar que o corpo que está mais próximo do
ponto de partida no instante t = 10s é o representado na alternativa:
a) corpo 1
b) corpo 4
c) corpo 2
d) corpo 3
16. (Pucpr 2010) Um motociclista dirige uma motocicleta ao longo de uma estrada reta como
mostrado no diagrama velocidade x tempo.
A respeito dessa situação, assinale a alternativa correta:
a) Entre os instantes t = 3 s e t = 5 s o movimento é acelerado.
b) A aceleração no intervalo de tempo entre t = 5 s e t = 7 s vale – 4 m/s2.
c) O deslocamento do motociclista entre os instantes t = 3 s e t = 5 s foi de 20 m.
d) A aceleração no intervalo de tempo entre t = 5 s e t = 7 s vale 2 m/s2 .
e) A aceleração no intervalo de tempo entre t = 0 e t = 3 s é nula.
17. (Ufmg 2009) Numa corrida, Rubens Barrichelo segue atrás de Felipe Massa, em um trecho
da pista reto e plano. Inicialmente, os dois carros movem-se com velocidade constante, de
mesmos módulos, direção e sentido. No instante t1 , Felipe aumenta a velocidade de seu carro
com aceleração constante; e, no instante t 2 , Barrichelo também aumenta a velocidade do seu
carro com a mesma aceleração.
Considerando essas informações, assinale a alternativa cujo gráfico melhor descreve o módulo
da velocidade relativa entre os dois veículos, em função do tempo
a)
Página 8 de 26
b)
c)
d)
18. (Uel 2009) O gráfico da velocidade em função do tempo, mostrado a seguir, descreve o
movimento de uma partícula em uma dimensão.
Com base nos conhecimentos sobre o tema, considere as afirmativas a seguir.
I - A partícula se desloca no sentido positivo, no intervalo entre os instantes t1 e t2.
II - A aceleração da partícula assume o valor zero no instante t2.
III - O deslocamento da partícula no intervalo t1 < t < t3 pode ser determinado por dois
processos matemáticos: por uma função horária e pelo cálculo da área da região entre o
gráfico descrito, no intervalo dado, e o eixo dos tempos.
IV - Por meio do gráfico apresentado, é possível saber a distância descrita pela partícula.
Assinale a alternativa CORRETA.
a) Somente as afirmativas I e II são corretas.
b) Somente as afirmativas I e IV são corretas.
c) Somente as afirmativas III e IV são corretas.
Página 9 de 26
d) Somente as afirmativas I, II e III são corretas.
e) Somente as afirmativas II, III e IV são corretas.
19. (Uerj 2009) A velocidade de um corpo que se desloca ao longo de uma reta, em função do
tempo, é representada pelo seguinte gráfico:
Calcule a velocidade média desse corpo no intervalo entre 0 e 30 segundos.
20. (Ufrj 2009) Um móvel parte do repouso e descreve uma trajetória retilínea durante um
intervalo de tempo de 50s, com a aceleração indicada no gráfico a seguir.
a) Faça um gráfico da velocidade do móvel no intervalo de 0 até 50s.
b) Calcule a distância percorrida pelo móvel nesse intervalo.
21. (Ufc 2008) Um trem, após parar em uma estação, sofre uma aceleração, de acordo com o
gráfico da figura a seguir, até parar novamente na próxima estação. Assinale a alternativa que
apresenta os valores corretos de tf, o tempo de viagem entre as duas estações, e da distância
entre as estações.
Página 10 de 26
a) 80 s, 1600 m
b) 65 s, 1600 m
c) 80 s, 1500 m
d) 65 s, 1500 m
e) 90 s, 1500 m
22. (Unesp 2008) Os movimentos de dois veículos, I e II, estão registrados nos gráficos da
figura.
Sendo os movimentos retilíneos, a velocidade do veículo II no instante em que alcança I é
a) 15 m/s.
b) 20 m/s.
c) 25 m/s.
d) 30 m/s.
e) 35 m/s.
23. (Ufpe 2007) Em t = 0, um objeto parte do repouso a partir da posição x = 1,0 m,
executando um movimento retilíneo, com aceleração em função do tempo mostrada no gráfico
a seguir. Dos gráficos apresentados em seguida, indique qual representa corretamente a
dependência da velocidade com o tempo.
Página 11 de 26
a)
b)
c)
d)
e)
24. (Ufscar 2007) Um pequeno objeto, quando lançado verticalmente para cima, retorna ao
local de partida após ter decorrido o tempo 2t. Dos conjuntos de gráficos apresentados, aquele
que se pode adequar perfeitamente à situação descrita, supondo desprezível a ação resistiva
do ar, é
a)
b)
c)
d)
e)
25. (Ufrrj 2007) Os gráficos a seguir representam a velocidade e a posição de um objeto móvel
em função do tempo.
Página 12 de 26
Com base nos gráficos, determine a posição s1 correspondente ao instante t = 6s.
26. (Ufpb 2007) Uma partícula em movimento retilíneo tem sua velocidade, em função do
tempo, representada no gráfico a seguir.
De acordo com o gráfico, o instante de tempo no qual a partícula retorna à posição inicial,
correspondente a t = 0, é:
a) 3s
b) 6s
c) 9s
d) 12s
e) 15s
27. (Pucsp 2004) O gráfico representa a variação da velocidade, com o tempo, de um móvel
em movimento retilíneo uniformemente variado.
A velocidade inicial do móvel e o seu deslocamento escalar de 0 a 5,0 s valem,
respectivamente:
a) - 4,0 m/s e - 5,0 m
Página 13 de 26
b) - 6,0 m/s e - 5,0 m
c) 4,0 m/s e 25 m
d) - 4,0 m/s e 5,0 m
e) - 6,0 m/s e 25 m
28. (Uerj 2003) O gráfico a seguir representa a variação da velocidade v em relação ao tempo
t de dois móveis A e B, que partem da mesma origem.
A distância, em metros, entre os móveis, no instante em que eles alcançam a mesma
velocidade, é igual a:
a) 5
b) 10
c) 15
d) 20
29. (Uece 1996) Um móvel desloca-se sobre uma reta, segundo o gráfico:
No intervalo t = 0 a t = 1, a aceleração foi______ e no intervalo t = 1 a t = 3, o espaço
percorrido foi______.
O preenchimento, na ordem das lacunas, é:
a) 1 m/s2; 4 m
b) 1 m/s2; 8 m
c) 2 m/s2; 4 m
d) 2 m/s2; 8 m
30. (Ufpe 1996) A velocidade de um objeto que se move ao longo de uma linha reta horizontal
está representada em função do tempo na figura a seguir. Qual o deslocamento, em metros, do
objeto após os primeiros 5 segundos?
Página 14 de 26
Página 15 de 26
Gabarito:
Resposta da questão 1:
[E]
A distância (D) pedida é numericamente igual à área hachurada no gráfico.
D
50  20
 10  D  350 m.
2
Resposta da questão 2:
[E]
1. Incorreta. Não podemos afirmar sobre o movimento nos primeiros 3 km, pois só temos
informações pontuais.
Resposta da questão 3:
[B]
Para calcular o deslocamento do jipe-robô, usamos a propriedade do gráfico v  t, calculando a
“área” destacada no gráfico abaixo.
ΔS 
20  15
15  10
10  7,5
10  5
5 5
 15 
 5  10  10  2 
5 
 10 

2
2
2
2
2
ΔS  262,5  62,5  100  87,5  75  12,5  600 cm 
ΔS  6 m.
Resposta da questão 4:
[B]
Analisando cada um dos trechos:
[I] o módulo da velocidade escalar cresce linearmente com o tempo: o movimento é
Página 16 de 26
uniformemente variado, acelerado.
[II] o módulo da velocidade escalar é constante e não nulo: o movimento é uniforme.
[III] o módulo da velocidade escalar decresce linearmente com o tempo: o movimento é
uniformemente variado, retardado.
Resposta da questão 5:
[D]
A “área” no diagrama vt é numericamente igual ao espaço percorrido (d).
Dividimos a figura em 2 partes e calculamos a “área” da seguinte forma:
d  A1  trapézio   A2 retângulo   10  2  1/2 10  1  6  10  16 km.
Mas o tempo total gasto é t = 2 h.
Então a velocidade média é:
vm  d/t  16/2  8 km/h.
Resposta da questão 6:
[A]
No gráfico da velocidade em função do tempo, a “área” (A) entre a linha do gráfico e o eixo t dá
o deslocamento escalar.
ΔS  ΔS01  ΔS12 
1 40 
2

1 40 
2
 20  20 
ΔS  0.
Resposta da questão 7:
[C]
As áreas da figura abaixo representam o deslocamento. Como uma é positiva e a outra
negativa de mesmo módulo, o deslocamento total é nulo.
Resposta da questão 8:
[C]
O enunciado nos pede a relação entre os deslocamentos BC e AB, ou seja:
SBC
 ?.
SAB
Lembrando que o valor da área da figura de um gráfico Vxt é igual à intensidade do
deslocamento do corpo, teremos:
Página 17 de 26
Área 1 = SAB , que ocorreu entre 0 e t1.
Área 1 = SAB  b.h  (t1  0).(V0  0)  t1.V0
Área 2 = SBC , que ocorreu entre t1e t2.
Área 2 = SBC 
SBC

SAB
b.h (t 2  t1).(V0  0) (t 2  t1).V0


2
2
2
(t 2  t1).V0
(t  t ).V
t t
1
2
 2 1 0.
 2 1
t1.V0
2
t1.V0
2.t1
Resposta da questão 9:
[C]
1º Trecho: movimento acelerado (a > 0)  o gráfico da posição em função do tempo é uma
curva de concavidade para cima.
2º Trecho: movimento uniforme (a = 0)  o gráfico da posição em função do tempo é um
segmento de reta crescente.
3º Trecho: movimento desacelerado (a < 0)  o gráfico da posição em função do tempo é
uma curva de concavidade para baixo.
Resposta da questão 10:
[D]
Considerando que os carros B e P iniciem seus movimentos no mesmo espaço e no mesmo
instante t0 (instante em que o carro B passa pelos policiais e a perseguição se inicia), eles irão
se encontrar novamente quando percorrerem o mesmo deslocamento no mesmo intervalo de
tempo, ou seja: SB  SP e tB  tP .
Conseguiremos encontrar o deslocamento de cada carro através da área do gráfico, já que o
gráfico dado é de velocidade em função do tempo.
Analisando o gráfico dado, concluímos que as áreas serão iguais em t4:
Página 18 de 26
Resposta da questão 11:
[B]
Note que entre 3 e 8 min a posição não varia. Portanto, o carro está parado.
Resposta da questão 12:
[D]
A área da figura sombreada é numericamente igual ao deslocamento.
ΔS  30  60  27  117km .
Vm 
ΔS 117
117

km / h 
m / s  6,5m / s .
Δt
5
5x3,6
Resposta da questão 13:
[D]
Pelo gráfico, percebe-se que o motorista imprudente é o condutor do veículo A, que recebe
acelerações e desacelerações mais bruscas.
30  10 20
 |a(I)| = 2,0 m/s2.

20  10 10
0  30
30

De 30 s a 40 s: a(II) =
 a(II) = 3,0 m/s2.
40  30
10
De 10 s a 20 s: |a(I)| =
Página 19 de 26
Resposta da questão 14:
[C]
Analisando o gráfico:
No instante t = 30 min, Tânia está passando pelo km 12, onde fica a igreja. Ângela passa por
esse marco no instante t = 40 min, isto é, 10 min após o telefonema. No instante t = 40 min,
Tânia está no km 16, ou seja, 4 km à frente de Ângela.
Resposta da questão 15:
[D]
As áreas das figuras sombreadas são numericamente iguais aos deslocamentos dos corpos.
Página 20 de 26
10  5
 25m  o corpo 1 está a 25m da posição inicial
2
10  5
S2 
 25m  o corpo 2 está a 25m da posição inicial
2
50
7.
 20
t.5 (10  t).2 5t  2t  20 7t  20
7
S3 




 15m
2
2
2
2
2
S1 
 o corpo 3 está a 15m da posição inicial
S4  10.(2)  20m  o corpo 2 está a 20m da posição inicial
Resposta da questão 16:
[B]
Analisemos cada intervalo:
– De 0 a 3 s: o movimento é uniformemente acelerado; a aceleração escalar é
a1 =
v1 8
  2,7 m/s2.
t1 3
O espaço percorrido é calculado pela “área” de 0 a 3 s
38
S1 
 12 m.
2
Página 21 de 26
– De 3 s a 5 s: o movimento é uniforme, com velocidade escalar v2 = 8 m/s.
O espaço percorrido é:
S2 = v2 t2  8  2 = 16 m.
– De 5 s s 7 s: o movimento é uniformemente retardado; a aceleração escalar é:
a3 =
v 3 0  8 8


 4 m/s2.
t 3 7  5
2
O espaço percorrido é:
28
S3 
 8 m.
2
Resposta da questão 17:
[A]
Antes do instante t1 , os veículos apresentam a mesma velocidade em relação ao solo e, desta
forma, apresentam velocidade relativa nula. Isto pode ser observado em todas as alternativas.
Entre o instante t1 e t 2 apenas o carro de Felipe está acelerado e, deste modo, a distância
entre os carros aumenta, o que significa que a velocidade relativa aumenta. Como este
aumento é linear, visto que a aceleração é constante, neste intervalo entre t1 e t 2 , a linha de
gráfico deverá ser retilínea e crescente. Isto pode ser visto nas opções A e B.
A partir do instante t 2 , a velocidade do carro de Barrichelo começa a crescer no mesmo ritmo
da de Felipe, de modo que a velocidade relativa se fixa novamente. Desta forma, a alternativa
correta é a A.
Resposta da questão 18:
[E]
Resolução
Entre os instantes 1 e 2 a velocidade é negativa e desta forma a partícula viaja no sentido
negativo do eixo.
No instante 2 a partícula muda o sinal de sua velocidade e consequentemente muda o sentido
de seu movimento. Para isto precisa, ainda que momentaneamente entrar em repouso, visto
que seu movimento é unidimensional.
A área entre a linha de gráfico e o eixo do tempo neste diagrama também, como a função
horária, determina o deslocamento da partícula.
Resposta da questão 19:
No diagrama de velocidade versus tempo, como o que temos, a distância total percorrida em
dado intervalo de tempo corresponde numericamente a área entre a linha de gráfico e o eixo
dos tempos.
Neste problema a distância total percorrida corresponde a soma das áreas dos retângulos e do
trapézio. Assim:
S = 10.5 + (5+15).(20-10)/2 + (30-20).15 = 50 + 100 + 150 = 300 m
A velocidade média é v = S/t = 300/30 = 10 m/s
Resposta da questão 20:
a) Observe o gráfico
Página 22 de 26
É interessante notar que como o movimento é caracterizado por duas acelerações, uma de 0 a
20 s e outra de 20 s a 50 s, o diagrama da velocidade manterá esta característica com uma
velocidade crescente no primeiro trecho (pois a aceleração é positiva) e uma velocidade
decrescente no segundo trecho.
b) A distância percorrida é 1150m.
Este mesmo diagrama pode nos fornecer a distância percorrida, pois esta é numericamente a
área entre a linha de gráfico e o eixo das abscissas. Assim: S = 20.40/2 + (10 + 40).(50 - 20) /
2 = 800/2 + 1500/2 = 400 + 750 = 1150 m
Resposta da questão 21:
[A]
Resposta da questão 22:
[D]
Resposta da questão 23:
[E]
A velocidade varia de 0 a 2s o equivalente área sombreada (1,0m/s) e de 2 a 4s fica constante,
pois a aceleração é nula.
Página 23 de 26
Resposta da questão 24:
[D]
Supondo para baixo a orientação da trajetória e sabendo que o movimento é uniforme optamos
pela letra D. A aceleração é constante e positiva. A velocidade varia linearmente com o tempo
a partir de uma velocidade inicial negativa e a posição varia segundo uma função do segundo
grau, cujo gráfico é uma parábola com concavidade voltada para cima.
Resposta da questão 25:
A aceleração do movimento é igual ao coeficiente angular da reta que representa a
velocidade, ou seja: a = ∆v/∆t =
 20
 10 
5
= 2 m/s2.
O movimento é uniformemente variado e sua função horária é:
s(t) = s(0) + v(0)t +
at 2
= 10 t + t2. Para t = 6, temos s( 6 ) = s1 = 10 × 6 + 36 = 96 m.
2
Resposta da questão 26:
[C]
De zero a 5s a partícula desloca-se em um sentido e a partir daí inverte. Para que ela volte à
posição inicial o deslocamento em um sentido deve ser, em módulo, igual ao sentido contrário.
Para isto as áreas sombreadas devem ter o mesmo valor numérico.
 5  210  t  5  t  6 10
2

2
 7  2t  11  t  9,0s
Resposta da questão 27:
[B]
Calculemos primeiro a aceleração entre 3,0s e 5,0s.
a
V 4  0

 2,0m / s2
t 5  3
A equação das velocidades do MUV é:
Página 24 de 26
V  V0  at
Observe que para t = 3,0s, V = 0  0  V0  2  3  V0  6,0m / s
A área sombreada da figura nos dá o deslocamento.
S 
3x( 6) 2x4

 5,0m
2
2
Resposta da questão 28:
[C]
Resposta da questão 29:
[B]
Resposta da questão 30:
12 m
Página 25 de 26
Página 26 de 26